用例举法求概率(云南省昆明市五华区实验中学)
文档属性
| 名称 | 用例举法求概率(云南省昆明市五华区实验中学) |  | |
| 格式 | rar | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-06 18:19:00 | ||
图片预览





文档简介
课件17张PPT。 通常要求一件事情的概率就可以经过大量重复实验,用其发生的频率去估算事情发生的概率。思考:怎样求一件事情的概率? 今天,我们研究一种特殊类型的
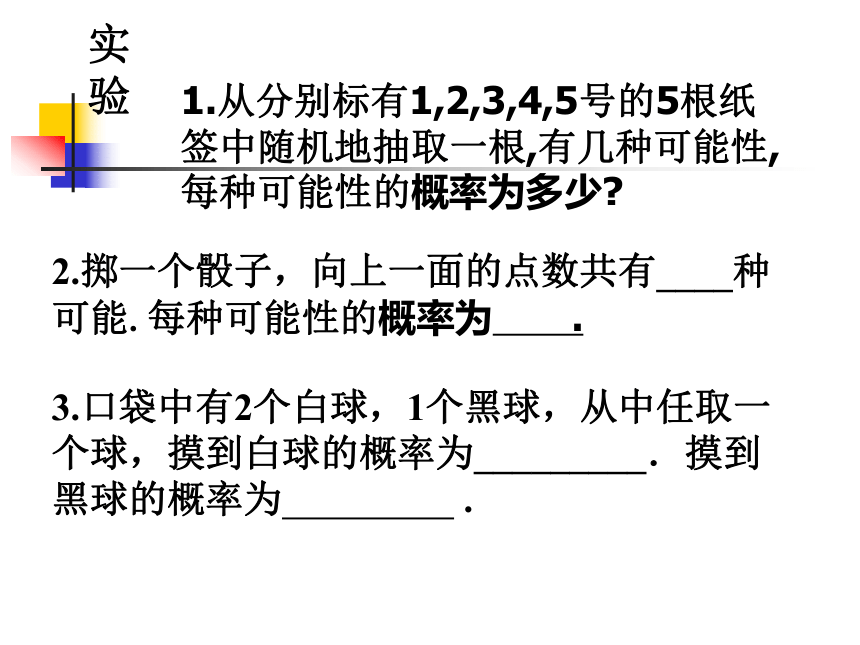
概率——古典概率实验1.从分别标有1,2,3,4,5号的5根纸签中随机地抽取一根,有几种可能性,每种可能性的概率为多少?2.掷一个骰子,向上一面的点数共有____种可能.每种可能性的概率为 .3.口袋中有2个白球,1个黑球,从中任取一个球,摸到白球的概率为_________.摸到黑球的概率为 .上面的问题中,都有两个共同的特点:
在一次实验中,可能出现的结果有限多个.
2) 在一次实验中,各种结果发生的可能性相等.称之为古典概率或者古典概型古典概率的计算方法一般地,如果在一次实验中,有n种可能的结果,并且它们发生的可能性相等,事件A包含其中的m种结果,那么事件A发生的概率为:
例1.掷一个骰子,观察向上一面的点数,求下列事件的概率:
(1)点数为2;
(2) 点数为奇数;
(3) 点数大于2小于5. 思考:它属不属于古典概率?如果是,我们
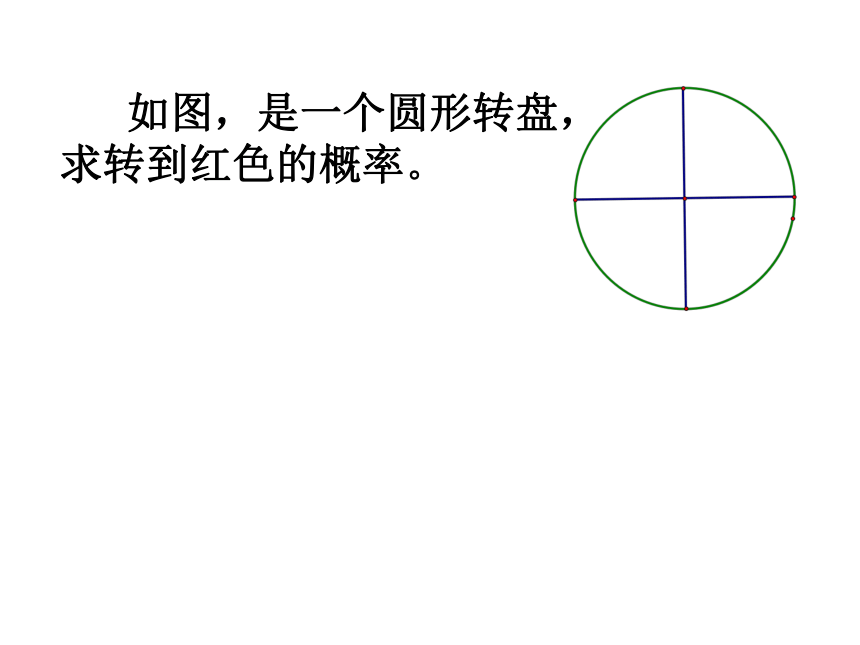
可以怎么计算? 如图,是一个圆形转盘,
求转到红色的概率。 如图,是一个圆形转盘,
求转到红色的概率。红1红2红3例2.如图,转盘分成6个相等的扇形,分为红、绿、黄三种颜色,指针固定在圆心,转动转盘让其自由停止,其中某个扇形会恰好停在指针所指的位置(在交线时当作指向右边的扇形)。求下列事件的概率:
(1)指针指向黄色。
(2)指针指向黄色或红色。
(3)指针不指向黄色。黄1黄2黄3绿1绿2例3.掷两枚均匀的硬币,求下列事件的概率:
(1)两枚正面都朝上 ;
(2)两枚反面都朝上 ;
(3)一枚正面朝上,另一枚反面朝上。注意:用列举法求解的步骤例4 在一个有9×9个小方
格中的正方形雷区中,随
机埋藏着10颗地雷,每
个小方格内最多只能藏1
颗地雷。3 小王在开始时地随机地
踩中一个方格,踩中后出
现了如图所示的情况。 数字3表示在A区域中有
3颗雷。那么第二步应该
踩在A区域还是B区域?AB例.掷两枚均匀的硬币,求下列事件的概率:
(1)两枚正面都朝上 ;
(2)两枚反面都朝上 ;
(3)一枚正面朝上,另一枚反面朝上。 例5 同时掷两个质地均匀的骰子,计算下列事件的概率: (1)两个骰子的点数相同; (2)两个骰子点数的和是9; (3)至少有一个骰子的点数为2. 问题1
列举时如何才能尽量避免重复和遗漏? 问题2
如果把例5中的“同时掷两个骰子”改为“把一个骰子掷两次”,所得到的结果有变化吗? 例6 甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从3个口袋中各随机地取出1个小球. (1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少? (2)取出的3个小球上全是辅音字母的概率是多少? 想一想,什么时候使用“列表法”方便,什么时候使用“树状图法”方便? 1.用列举法求概率的条件是:
(1)实验的结果是有限个(n)
(2)各种结果的可能性相等.小结:2.用列举法求概率的的公式是:
概率——古典概率实验1.从分别标有1,2,3,4,5号的5根纸签中随机地抽取一根,有几种可能性,每种可能性的概率为多少?2.掷一个骰子,向上一面的点数共有____种可能.每种可能性的概率为 .3.口袋中有2个白球,1个黑球,从中任取一个球,摸到白球的概率为_________.摸到黑球的概率为 .上面的问题中,都有两个共同的特点:
在一次实验中,可能出现的结果有限多个.
2) 在一次实验中,各种结果发生的可能性相等.称之为古典概率或者古典概型古典概率的计算方法一般地,如果在一次实验中,有n种可能的结果,并且它们发生的可能性相等,事件A包含其中的m种结果,那么事件A发生的概率为:
例1.掷一个骰子,观察向上一面的点数,求下列事件的概率:
(1)点数为2;
(2) 点数为奇数;
(3) 点数大于2小于5. 思考:它属不属于古典概率?如果是,我们
可以怎么计算? 如图,是一个圆形转盘,
求转到红色的概率。 如图,是一个圆形转盘,
求转到红色的概率。红1红2红3例2.如图,转盘分成6个相等的扇形,分为红、绿、黄三种颜色,指针固定在圆心,转动转盘让其自由停止,其中某个扇形会恰好停在指针所指的位置(在交线时当作指向右边的扇形)。求下列事件的概率:
(1)指针指向黄色。
(2)指针指向黄色或红色。
(3)指针不指向黄色。黄1黄2黄3绿1绿2例3.掷两枚均匀的硬币,求下列事件的概率:
(1)两枚正面都朝上 ;
(2)两枚反面都朝上 ;
(3)一枚正面朝上,另一枚反面朝上。注意:用列举法求解的步骤例4 在一个有9×9个小方
格中的正方形雷区中,随
机埋藏着10颗地雷,每
个小方格内最多只能藏1
颗地雷。3 小王在开始时地随机地
踩中一个方格,踩中后出
现了如图所示的情况。 数字3表示在A区域中有
3颗雷。那么第二步应该
踩在A区域还是B区域?AB例.掷两枚均匀的硬币,求下列事件的概率:
(1)两枚正面都朝上 ;
(2)两枚反面都朝上 ;
(3)一枚正面朝上,另一枚反面朝上。 例5 同时掷两个质地均匀的骰子,计算下列事件的概率: (1)两个骰子的点数相同; (2)两个骰子点数的和是9; (3)至少有一个骰子的点数为2. 问题1
列举时如何才能尽量避免重复和遗漏? 问题2
如果把例5中的“同时掷两个骰子”改为“把一个骰子掷两次”,所得到的结果有变化吗? 例6 甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从3个口袋中各随机地取出1个小球. (1)取出的3个小球上恰好有1个、2个和3个元音字母的概率分别是多少? (2)取出的3个小球上全是辅音字母的概率是多少? 想一想,什么时候使用“列表法”方便,什么时候使用“树状图法”方便? 1.用列举法求概率的条件是:
(1)实验的结果是有限个(n)
(2)各种结果的可能性相等.小结:2.用列举法求概率的的公式是:
同课章节目录
