第三章 一元一次方程(测能力)(含解析)——2023-2024学年人教版数学七年级上册单元闯关双测卷
文档属性
| 名称 | 第三章 一元一次方程(测能力)(含解析)——2023-2024学年人教版数学七年级上册单元闯关双测卷 |

|
|
| 格式 | docx | ||
| 文件大小 | 456.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 00:00:00 | ||
图片预览




文档简介
第三章 一元一次方程(测能力)——2023-2024学年人教版数学七年级上册单元闯关双测卷
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.下列方程为一元一次方程的是( )
A. B.
C. D.
2.某轮船沿江从A港顺流航行到B港,比从B港逆流返回A港少用,已知船在静水中的速度为,水流速度为.设A港和B港相距,根据题意可列方程( )
A. B.
C. D.
3.下列变形正确的是( )
A.由,得 B.由,得
C.由,得 D.由,得
4.若的值比的值小1,则x的值为( )
A.-5 B.-1 C.-3 D.
5.一个两位数,个位数字与十位数字的和为9,若将个位数字与十位数字对调后所得新数比原数小9,则原两位数是( )
A.45 B.27 C.72 D.54
6.小明在解方程去分母时,方程右边的没有乘3,因而求得的解为,则原方程的解为( )
A. B. C. D.
7.《算法统宗》中记载了一个“李白沽酒”的故事,诗云:“今携一壶酒,游春郊外走,逢朋加一倍,入店饮半斗,相逢三处店,饮尽壶中酒.试问能算士,如何知原有.”(注:古代一斗是10升)译文:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的5升酒.按照这样的约定,在第3个店里遇到朋友后,李白正好喝光了壶中的酒,请问各位,壶中原有___升酒( )
A. 5 B. C. D.
8.下列变形正确的( )
A.方程未知数化为1,得
B.方程移项,得
C.方程去括号,得
D.方程可化成
9.从-3,-2,-1,1,2,3中选一个数作为k的值,使得关于x的方程的解为整数,则所有满足条件的k的值的积为( )
A.-4 B.-12 C.18 D.36
10.如图,在2022年2月的月历表中用“Y”字形的框框出1,3,8,10,16这五个数,它们的和为38.若移动这个框的位置又框出新的五个数,已知这新的五个数的和是48,则其中最小的两个数的和是( )
A.7 B.8 C.9 D.18
二、填空题(每小题4分,共20分)
11.某商品每件的进价为10元,若按标价打八折出售,每件可获利2元,则该商品的标价为每件__________元.
12.方程的解是__________
13.一项工作,甲单独做需9天完成,乙单独做需12天完成,如果两人合做几天后,余下的工作再由甲单独做2天完成,则甲、乙两人合做了_______天.
14.已知关于x一元一次方程的解是,那么关于y的一元一次方程的解是_________.
15.有一列数,按一定的规律排列:,2,,8,,32,,128,……,若其中某三个相邻的数之和为384,则这三个数中最小的数是__________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)解方程:
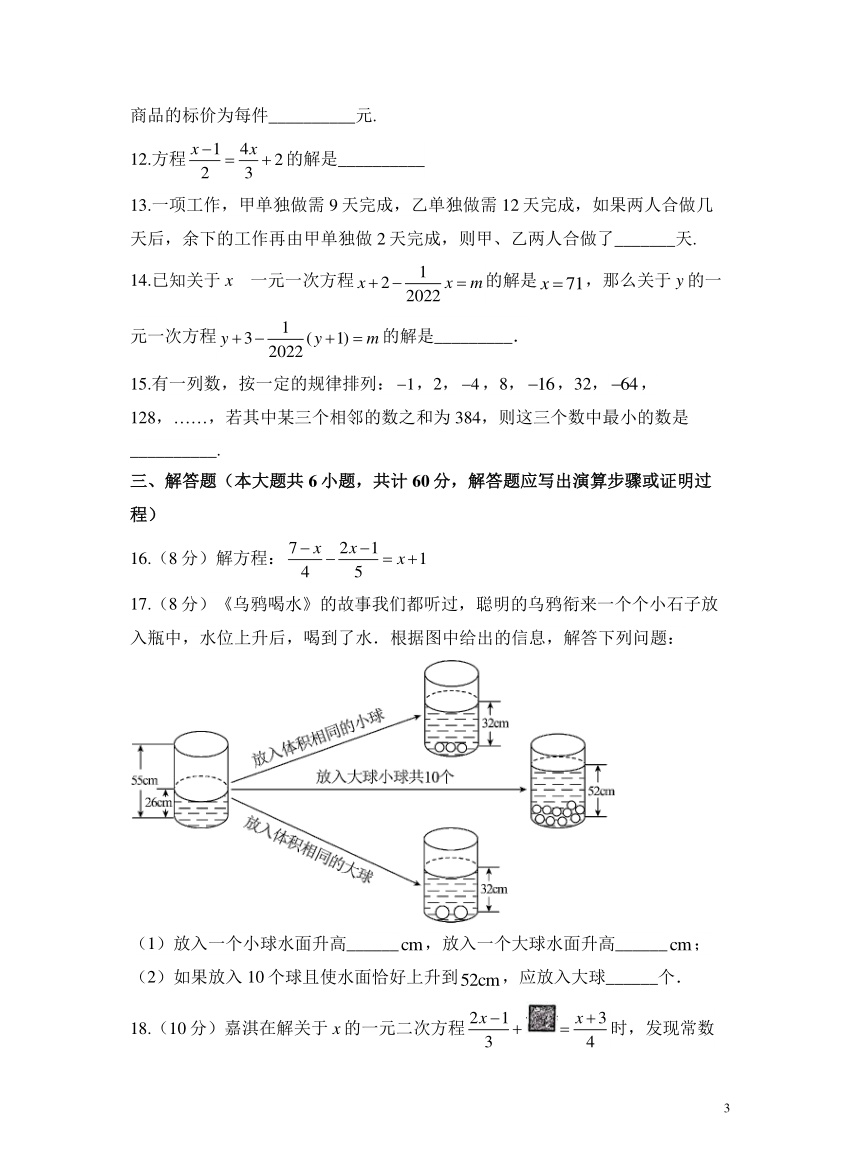
17.(8分)《乌鸦喝水》的故事我们都听过,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,喝到了水.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高______,放入一个大球水面升高______;
(2)如果放入10个球且使水面恰好上升到,应放入大球______个.
18.(10分)嘉淇在解关于x的一元二次方程时,发现常数被污染了;
(1)嘉淇猜是-1,请解一元一次方程
(2)老师告诉嘉淇这个方程的解为,求被污染的常数。
19.(10分)分别观察下面的两组等式:
根据你发现的规律解决下列问题:
(1)填空:_____;
(2)已知,则x的值是______;
(3)设满足上面特征的等式最左边的数为y,求y的最大值,并写出此时的等式.
20.(12分)某市为建设节约型社会、实现可持续发展,根据国家“阶梯电价”的有关文件要求,决定对居民生活用电实施“阶梯电价”收费,具体收费标准见下表.实施“阶梯电价”收费以后,居民陈先生家10月份用电100 kW·h,缴电费50元.
一户居民一个月的用电量 电费价格[单位:元/kW·h]
不超过150 kW·h的部分 a
超过150 kW·h,但不超过300 kW·h的部分 0.6
超过300 kW·h的部分
(1)__________.
(2)若陈先生家11月份用电,应缴电费多少元?
(3)在(2)的条件下,若陈先生家12月份与11月份的电费相差80元,求陈先生家12月份的用电量.
21.(12分)观察下列两个等式:.给出定义如下:我们称使等式成立的一对有理数a,b为“同心有理数对”,记为.如:数对,都是“同心有理数对”.
(1)数对,是“同心有理数对”的是____;
(2)若是“同心有理数对”,求a的值;
(3)若是“同心有理数对”,则______(填“是”或“不是”)“同心有理数对”,说明理由.
答案以及解析
1.答案:A
解析:A、是一元一次方程,本选项符合题意;
B、是二元一次方程,本选项不符合题意;
C、不是方程,本选项不符合题意;
D、不是整式方程,本选项不符合题意.
故选:A.
2.答案:B
解析:由题意得,即.
3.答案:D
解析:A、由,得,变形错误,该选项不符合题意;
B、由,得,变形错误,该选项不符合题意;
C、由,得,变形错误,该选项不符合题意;
D、变形正确,该选项符合题意.
故选:D.
4.答案:A
解析:因为的值比的值小1,所以,解得.
5.答案:D
解析:设原两位数的个位数字是x,则十位数字是.根据题意得,解得,所以,所以原两位数为54.
6.答案:A
解析:根据题意,得.把代入这个方程,得,解得.把代入原方程,得.去分母,得,移项、合并同类项,得.故选A.
7.答案: D
解析:设壶中原有x升酒,由题意得,
,
故选D.
8.答案:B
解析:A.方程未知数化为1,得,故选项错误;
B.方程移项,得,正确;
C、方程,去括号得:,故选项错误;
D、方程可化成,故选项错误.
故选:B.
9.答案:A
解析:,
,
,
,
,
方程的解为整数,
,2
所有满足条件的k的值的积-4,
故选:A.
10.答案:B
解析:设最小的数是x,则另外四个数从小到大依次为,,,,根据题意得,解得,所以,所以,即最小的两个数的和是8.
11.答案:15
解析:设该商品的标价为每件x元.
由题意,得,解得,
该商品的标价为每件15元.
12.答案:
解析:,
去分母得:,
去括号得:,
移项:,
合并:,
系数化1得:;
故答案为:.
13.答案:4
解析:设甲、乙两人合做了x天,
可得方程:,
解得:,
答:甲、乙两人合做了4天.
故答案为:4.
14.答案:
解析: ,
.
关于x的一元一次方程的解是,
关于的一元一次方程的解为:,
解得:,
故答案为:.
15.答案:-256
解析:设中间的数为x,则前面的数是,后面的数是,依题意得,解得,则前面的数是128,后面的数是512,故这三个数中最小的是-256.
16.答案:
解析:,
去分母,得:,
去括号,得:,
移项,得:,
合并同类项,得:,
系数化1,得:.
17.答案: (1)2 ,3
(2)6
解析:(1)①设放入一个小球使水面升高,根据题意列出方程,
有图形得:,
解得: ;
②设放入一个大球使水面升高,根据题意列出方程,
由图形得:,
解得:;
故答案为:2,3.
(2)设放入大球m个,小球个,根据题意得,
,
解得:,
答:应放入大球6个;
故答案为:6.
18.答案:(1);
(2)4;
解析:(1)
去分母得:
去括号得:
移项,得
合并同类项,得
系数化为1,得;
(2)设“”的常数为m,由于是方程的解,则
,解之得,
所以被污染的常数是4.
19.答案:(1),,故答案为5.
(2)依题意有或.故x的值是10或-12.
(3)设绝对值符号里左边的数为a.
由题意得,所以.
因为的最小值为0,所以的最小值为0,所以y的最大值为7.
此时,所以,所以此时等式为.
答:y的最大值为7,此时的等式为.
20.答案:(1)0.5
(2)陈先生家11月份应缴电费153元
(3)陈先生家12月份的用电量是或
解析:(1).
(2)因为,
所以应缴电费为(元).
答:陈先生家11月份应缴电费153元.
(3)由题意可知,陈先生家12月份的电费为233元或73元.
设陈先生家12月份的用电量是.
如果,那么电费为(元);
如果,那么电费为(元).
①当电费为73元时,由题意得,
解得.
②当电费为233元时,由题意得,
解得.
综上所述,陈先生家12月份的用电量是或.
21.答案:(1)因为,,
,所以数对不是“同心有理数对”.
因为,,所以,
所以是“同心有理数对”.
故答案为.
(2)因为是“同心有理数对”,
所以,等式两边同时减去a,得,
整理得.等式两边同时加上1,得,
整理得.等式两边同时除以5,得.
(3)是.理由:因为是“同心有理数对”,
所以.
因为,所以是“同心有理数对”.
1
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.下列方程为一元一次方程的是( )
A. B.
C. D.
2.某轮船沿江从A港顺流航行到B港,比从B港逆流返回A港少用,已知船在静水中的速度为,水流速度为.设A港和B港相距,根据题意可列方程( )
A. B.
C. D.
3.下列变形正确的是( )
A.由,得 B.由,得
C.由,得 D.由,得
4.若的值比的值小1,则x的值为( )
A.-5 B.-1 C.-3 D.
5.一个两位数,个位数字与十位数字的和为9,若将个位数字与十位数字对调后所得新数比原数小9,则原两位数是( )
A.45 B.27 C.72 D.54
6.小明在解方程去分母时,方程右边的没有乘3,因而求得的解为,则原方程的解为( )
A. B. C. D.
7.《算法统宗》中记载了一个“李白沽酒”的故事,诗云:“今携一壶酒,游春郊外走,逢朋加一倍,入店饮半斗,相逢三处店,饮尽壶中酒.试问能算士,如何知原有.”(注:古代一斗是10升)译文:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的5升酒.按照这样的约定,在第3个店里遇到朋友后,李白正好喝光了壶中的酒,请问各位,壶中原有___升酒( )
A. 5 B. C. D.
8.下列变形正确的( )
A.方程未知数化为1,得
B.方程移项,得
C.方程去括号,得
D.方程可化成
9.从-3,-2,-1,1,2,3中选一个数作为k的值,使得关于x的方程的解为整数,则所有满足条件的k的值的积为( )
A.-4 B.-12 C.18 D.36
10.如图,在2022年2月的月历表中用“Y”字形的框框出1,3,8,10,16这五个数,它们的和为38.若移动这个框的位置又框出新的五个数,已知这新的五个数的和是48,则其中最小的两个数的和是( )
A.7 B.8 C.9 D.18
二、填空题(每小题4分,共20分)
11.某商品每件的进价为10元,若按标价打八折出售,每件可获利2元,则该商品的标价为每件__________元.
12.方程的解是__________
13.一项工作,甲单独做需9天完成,乙单独做需12天完成,如果两人合做几天后,余下的工作再由甲单独做2天完成,则甲、乙两人合做了_______天.
14.已知关于x一元一次方程的解是,那么关于y的一元一次方程的解是_________.
15.有一列数,按一定的规律排列:,2,,8,,32,,128,……,若其中某三个相邻的数之和为384,则这三个数中最小的数是__________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)解方程:
17.(8分)《乌鸦喝水》的故事我们都听过,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,喝到了水.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高______,放入一个大球水面升高______;
(2)如果放入10个球且使水面恰好上升到,应放入大球______个.
18.(10分)嘉淇在解关于x的一元二次方程时,发现常数被污染了;
(1)嘉淇猜是-1,请解一元一次方程
(2)老师告诉嘉淇这个方程的解为,求被污染的常数。
19.(10分)分别观察下面的两组等式:
根据你发现的规律解决下列问题:
(1)填空:_____;
(2)已知,则x的值是______;
(3)设满足上面特征的等式最左边的数为y,求y的最大值,并写出此时的等式.
20.(12分)某市为建设节约型社会、实现可持续发展,根据国家“阶梯电价”的有关文件要求,决定对居民生活用电实施“阶梯电价”收费,具体收费标准见下表.实施“阶梯电价”收费以后,居民陈先生家10月份用电100 kW·h,缴电费50元.
一户居民一个月的用电量 电费价格[单位:元/kW·h]
不超过150 kW·h的部分 a
超过150 kW·h,但不超过300 kW·h的部分 0.6
超过300 kW·h的部分
(1)__________.
(2)若陈先生家11月份用电,应缴电费多少元?
(3)在(2)的条件下,若陈先生家12月份与11月份的电费相差80元,求陈先生家12月份的用电量.
21.(12分)观察下列两个等式:.给出定义如下:我们称使等式成立的一对有理数a,b为“同心有理数对”,记为.如:数对,都是“同心有理数对”.
(1)数对,是“同心有理数对”的是____;
(2)若是“同心有理数对”,求a的值;
(3)若是“同心有理数对”,则______(填“是”或“不是”)“同心有理数对”,说明理由.
答案以及解析
1.答案:A
解析:A、是一元一次方程,本选项符合题意;
B、是二元一次方程,本选项不符合题意;
C、不是方程,本选项不符合题意;
D、不是整式方程,本选项不符合题意.
故选:A.
2.答案:B
解析:由题意得,即.
3.答案:D
解析:A、由,得,变形错误,该选项不符合题意;
B、由,得,变形错误,该选项不符合题意;
C、由,得,变形错误,该选项不符合题意;
D、变形正确,该选项符合题意.
故选:D.
4.答案:A
解析:因为的值比的值小1,所以,解得.
5.答案:D
解析:设原两位数的个位数字是x,则十位数字是.根据题意得,解得,所以,所以原两位数为54.
6.答案:A
解析:根据题意,得.把代入这个方程,得,解得.把代入原方程,得.去分母,得,移项、合并同类项,得.故选A.
7.答案: D
解析:设壶中原有x升酒,由题意得,
,
故选D.
8.答案:B
解析:A.方程未知数化为1,得,故选项错误;
B.方程移项,得,正确;
C、方程,去括号得:,故选项错误;
D、方程可化成,故选项错误.
故选:B.
9.答案:A
解析:,
,
,
,
,
方程的解为整数,
,2
所有满足条件的k的值的积-4,
故选:A.
10.答案:B
解析:设最小的数是x,则另外四个数从小到大依次为,,,,根据题意得,解得,所以,所以,即最小的两个数的和是8.
11.答案:15
解析:设该商品的标价为每件x元.
由题意,得,解得,
该商品的标价为每件15元.
12.答案:
解析:,
去分母得:,
去括号得:,
移项:,
合并:,
系数化1得:;
故答案为:.
13.答案:4
解析:设甲、乙两人合做了x天,
可得方程:,
解得:,
答:甲、乙两人合做了4天.
故答案为:4.
14.答案:
解析: ,
.
关于x的一元一次方程的解是,
关于的一元一次方程的解为:,
解得:,
故答案为:.
15.答案:-256
解析:设中间的数为x,则前面的数是,后面的数是,依题意得,解得,则前面的数是128,后面的数是512,故这三个数中最小的是-256.
16.答案:
解析:,
去分母,得:,
去括号,得:,
移项,得:,
合并同类项,得:,
系数化1,得:.
17.答案: (1)2 ,3
(2)6
解析:(1)①设放入一个小球使水面升高,根据题意列出方程,
有图形得:,
解得: ;
②设放入一个大球使水面升高,根据题意列出方程,
由图形得:,
解得:;
故答案为:2,3.
(2)设放入大球m个,小球个,根据题意得,
,
解得:,
答:应放入大球6个;
故答案为:6.
18.答案:(1);
(2)4;
解析:(1)
去分母得:
去括号得:
移项,得
合并同类项,得
系数化为1,得;
(2)设“”的常数为m,由于是方程的解,则
,解之得,
所以被污染的常数是4.
19.答案:(1),,故答案为5.
(2)依题意有或.故x的值是10或-12.
(3)设绝对值符号里左边的数为a.
由题意得,所以.
因为的最小值为0,所以的最小值为0,所以y的最大值为7.
此时,所以,所以此时等式为.
答:y的最大值为7,此时的等式为.
20.答案:(1)0.5
(2)陈先生家11月份应缴电费153元
(3)陈先生家12月份的用电量是或
解析:(1).
(2)因为,
所以应缴电费为(元).
答:陈先生家11月份应缴电费153元.
(3)由题意可知,陈先生家12月份的电费为233元或73元.
设陈先生家12月份的用电量是.
如果,那么电费为(元);
如果,那么电费为(元).
①当电费为73元时,由题意得,
解得.
②当电费为233元时,由题意得,
解得.
综上所述,陈先生家12月份的用电量是或.
21.答案:(1)因为,,
,所以数对不是“同心有理数对”.
因为,,所以,
所以是“同心有理数对”.
故答案为.
(2)因为是“同心有理数对”,
所以,等式两边同时减去a,得,
整理得.等式两边同时加上1,得,
整理得.等式两边同时除以5,得.
(3)是.理由:因为是“同心有理数对”,
所以.
因为,所以是“同心有理数对”.
1
