第十二章 全等三角形(测能力)(含解析)——2023-2024学年人教版数学八年级上册单元闯关双测卷
文档属性
| 名称 | 第十二章 全等三角形(测能力)(含解析)——2023-2024学年人教版数学八年级上册单元闯关双测卷 |  | |
| 格式 | docx | ||
| 文件大小 | 991.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 22:03:08 | ||
图片预览


文档简介
第十二章 全等三角形(测能力)——2023-2024学年人教版数学八年级上册单元闯关双测卷
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.嘉琪在解决问题时,给出的推理过程如下:
如图,点D在AC上,点E在AB上,,. 求证:. 证明:在和中, , .
小明为了保证嘉琪的推理更严谨,想在方框中“,”和“.”之间作补充,下列说法正确的是( )
A.嘉琪的推理严谨,不需要补充 B.应补充“,”
C.应补充“,” D.应补充“,”
2.如图,在的正方形网格中,等于( )
A. B. C. D.
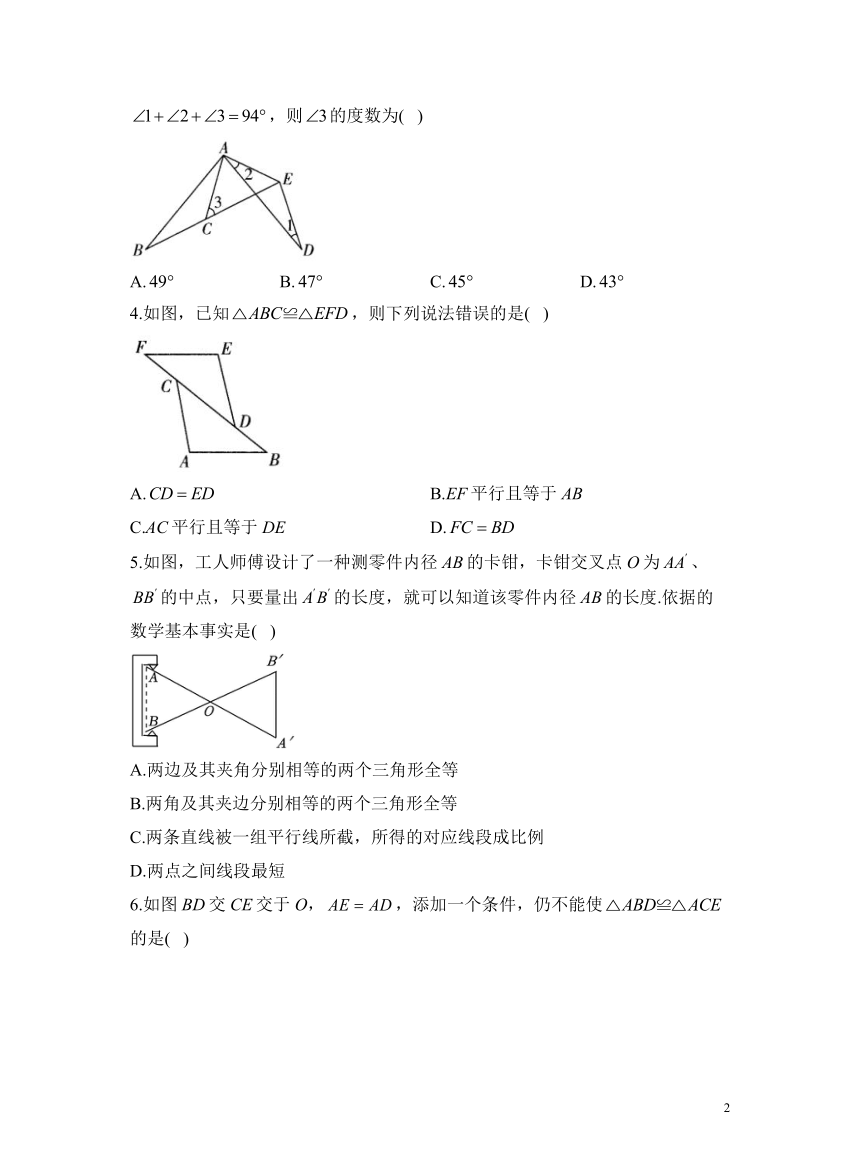
3.如图,已知B,C,E三点在同一直线上,,,.若,则的度数为( )
A. B. C. D.
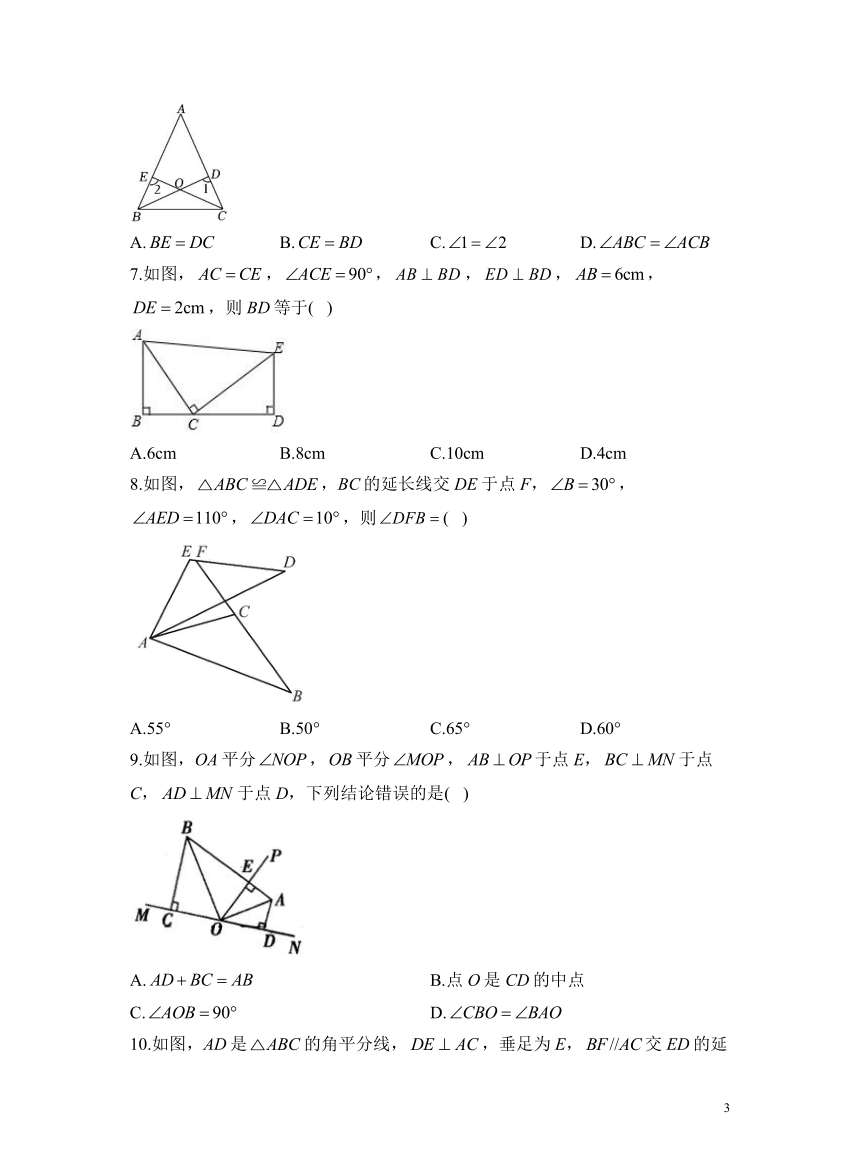
4.如图,已知,则下列说法错误的是( )
A. B.EF平行且等于AB
C.AC平行且等于DE D.
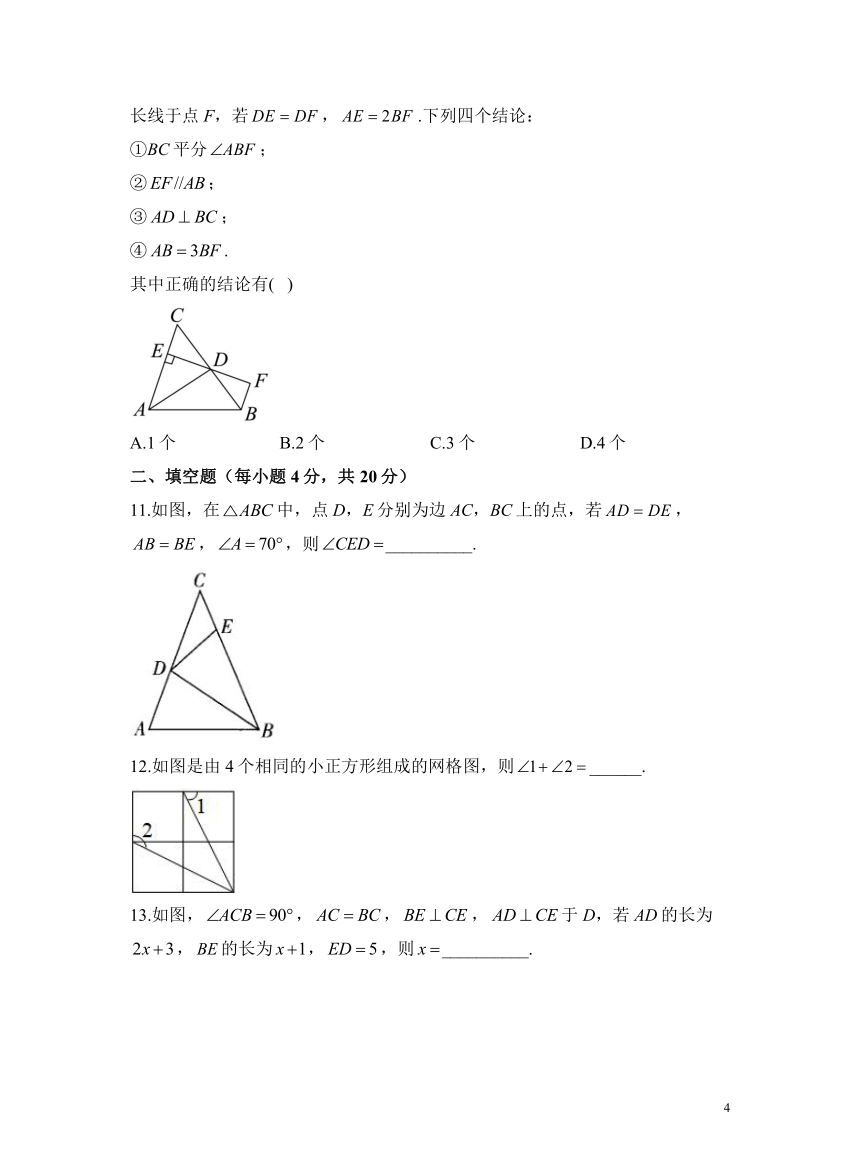
5.如图,工人师傅设计了一种测零件内径AB的卡钳,卡钳交叉点O为、的中点,只要量出的长度,就可以知道该零件内径AB的长度.依据的数学基本事实是( )
A.两边及其夹角分别相等的两个三角形全等
B.两角及其夹边分别相等的两个三角形全等
C.两条直线被一组平行线所截,所得的对应线段成比例
D.两点之间线段最短
6.如图BD交CE交于O,,添加一个条件,仍不能使的是( )
A. B. C. D.
7.如图,,,,,,,则BD等于( )
A.6cm B.8cm C.10cm D.4cm
8.如图,,BC的延长线交DE于点F,,,,则( )
A.55° B.50° C.65° D.60°
9.如图,OA平分,平分,于点E,于点C,于点D,下列结论错误的是( )
A. B.点O是CD的中点
C. D.
10.如图,AD是的角平分线,,垂足为E,交ED的延长线于点F,若,.下列四个结论:
①BC平分;
②;
③;
④.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题4分,共20分)
11.如图,在中,点D,E分别为边AC,BC上的点,若,,,则__________.
12.如图是由4个相同的小正方形组成的网格图,则______.
13.如图,,,,于D,若AD的长为,的长为,,则__________.
14.如图,已知四边形ABCD中,,,,,点E为线段AB的中点.如果点P在线段BC上以的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.当点Q的运动速度为__________时,能够使与全等.
15.如图中,,AD平分,于E,给出下列结论:
①;
②DA平分;
③DE平分;
④;
⑤;
其中正确的是______写序号.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,在中,于E,于D,.求证:.
17.(8分)如图,已知,点B,E,C,F在同一条直线上.
(1)若,,求的度数;
(2)若,,求BF的长.
18.(10分)课间,小明拿着老师的等腰直角三角板(,)玩,不小心掉到两墙之间(墙与地面垂直),三角板的直角顶点恰好着地,且D,C,E三点在同一直线上,如图所示.(A,B,C,D,E五点在同一平面内)
(1)求证:.
(2)已知,且图中每块砌墙砖的厚度均为,请你帮小明求出每块砌墙砖的厚度.
19.(10分)已知:,,.
(1)如图1当点D在AB上,________.
(2)如图2猜想与的面积有何关系?请说明理由.(温馨提示:两三角形可以看成是等底的)
20.(12分)如图,在四边形ABCD中,,点E是BC的中点,DE平分.
(1)求证:AE平分.
(2)判断AB,CD,AD之间的数量关系,并证明.
(3)已知,,求.
21.(12分)在中,,点D是线段CB上的一动点(不与点B,C重合),以AD为一边在AD的右侧作,使,,连接CE.
(1)如图(1),当点D在线段CB上,时,_________°.
(2)设,.如图(2),当点D在线段CB上,时,请你探究与之间的数量关系,并证明你的结论.
答案以及解析
1.答案:B
解析:,,,,,应该补充“,”.
2.答案:C
解析:如图,,,,,.,.
3.答案:B
解析:在和中,,,.又,,,.
4.答案:A
解析:,,,,故B选项正确.,,,,故C选项正确.,,,即,故D选项正确.故选A.
5.答案:A
解析:点O为、的中点,
,,
由对顶角相等得,
在和中,
,
,
,
即只要量出的长度,就可以知道该零件内径AB的长度,故选A.
6.答案:B
解析:,,
当时,则,依据SAS即可得到;
当时,则和全等条件是SSA,不能判定;
当时,由于,则,依据ASA即可得到;
当时,则,依据SAS即可得到;
故选B.
7.答案:B
解析:,,
,
,
,
,
,
在和中,
,
,
,,
,故选B.
8.答案:B
解析:,
,,
,
由三角形内角和为可知:,
,故选B.
9.答案:D
解析:平分,平分,,,,故选项C不合题意.在和中,,,,.同理可得,,,,点O是CD的中点,故选项A,B不合题意.故选D.
10.答案:C
解析:过D点作于H,如图,
AD是的角平分线,,,
,
,
,
,,
,
BC平分,所以①正确;
的度数不确定,
而,
不一定等于,
EF与AB不一定平行,所以②错误;
,
,
BD平分,
,
,
,
AD平分,
,所以③正确;
在和中,
,
,
,
在和中,
,
,
,
,
,
,所以④正确.故选C.
11.答案:
解析:在与中,,,.
12.答案:
解析:由题意得:,,,
所以,
,
所以.
13.答案:3
解析:,于D,,.,
.在和中,
,,.,且,,解得.
14.答案:3或
解析:设点P运动的时间为,则,,由,可分以下两种情况讨论.①当,时,,此时,解得,所以,此时点Q的运动速度为.②当,时,,此时,解得,此时点Q的运动速度为.
15.答案:①②④⑤
解析:,AD平分,,
,故①正确;
在和中,,
,
,,
DA平分,故②正确;
,故④正确;
,
,
,故⑤正确;
,而,
,
DE平分错误,故③错误;
综上所述,正确的有①②④⑤.
16.解析:证明:,,
.
在和中,
,
,
,
,
,
.
17.解析:(1),,
.
,.
(2),,
.
,,
.
18.解析:(1)证明:由题意得,,,
,,
.
在和中,
.
(2)由题意知,每块砌墙砖的厚度均为,
,..
由(1)得,
,,
,解得.
答:每块砌墙砖的厚度均为.
19.解析:(1),
,,
,,
,
,
,
故答案为:;
(2).
理由如下:作于F,作交EC的延长线于F,
,
,
,,
,,
,
在和中,
,
,
,
,
,
,,
.
20.解析:(1)证明:如图,过点E作于点F,
,平分,
.
E是BC的中点,
,
.
又,,
平分.
(2).
证明:,
在和中,
,.
同理可得,
.
,.
(3),点E是BC的中点,,.
,.
21.解析:(1),,
.
在和中,
,.
,.
(2).
证明:,
,
.
在和中,
,
.
,
,
.
1
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.嘉琪在解决问题时,给出的推理过程如下:
如图,点D在AC上,点E在AB上,,. 求证:. 证明:在和中, , .
小明为了保证嘉琪的推理更严谨,想在方框中“,”和“.”之间作补充,下列说法正确的是( )
A.嘉琪的推理严谨,不需要补充 B.应补充“,”
C.应补充“,” D.应补充“,”
2.如图,在的正方形网格中,等于( )
A. B. C. D.
3.如图,已知B,C,E三点在同一直线上,,,.若,则的度数为( )
A. B. C. D.
4.如图,已知,则下列说法错误的是( )
A. B.EF平行且等于AB
C.AC平行且等于DE D.
5.如图,工人师傅设计了一种测零件内径AB的卡钳,卡钳交叉点O为、的中点,只要量出的长度,就可以知道该零件内径AB的长度.依据的数学基本事实是( )
A.两边及其夹角分别相等的两个三角形全等
B.两角及其夹边分别相等的两个三角形全等
C.两条直线被一组平行线所截,所得的对应线段成比例
D.两点之间线段最短
6.如图BD交CE交于O,,添加一个条件,仍不能使的是( )
A. B. C. D.
7.如图,,,,,,,则BD等于( )
A.6cm B.8cm C.10cm D.4cm
8.如图,,BC的延长线交DE于点F,,,,则( )
A.55° B.50° C.65° D.60°
9.如图,OA平分,平分,于点E,于点C,于点D,下列结论错误的是( )
A. B.点O是CD的中点
C. D.
10.如图,AD是的角平分线,,垂足为E,交ED的延长线于点F,若,.下列四个结论:
①BC平分;
②;
③;
④.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题4分,共20分)
11.如图,在中,点D,E分别为边AC,BC上的点,若,,,则__________.
12.如图是由4个相同的小正方形组成的网格图,则______.
13.如图,,,,于D,若AD的长为,的长为,,则__________.
14.如图,已知四边形ABCD中,,,,,点E为线段AB的中点.如果点P在线段BC上以的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.当点Q的运动速度为__________时,能够使与全等.
15.如图中,,AD平分,于E,给出下列结论:
①;
②DA平分;
③DE平分;
④;
⑤;
其中正确的是______写序号.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,在中,于E,于D,.求证:.
17.(8分)如图,已知,点B,E,C,F在同一条直线上.
(1)若,,求的度数;
(2)若,,求BF的长.
18.(10分)课间,小明拿着老师的等腰直角三角板(,)玩,不小心掉到两墙之间(墙与地面垂直),三角板的直角顶点恰好着地,且D,C,E三点在同一直线上,如图所示.(A,B,C,D,E五点在同一平面内)
(1)求证:.
(2)已知,且图中每块砌墙砖的厚度均为,请你帮小明求出每块砌墙砖的厚度.
19.(10分)已知:,,.
(1)如图1当点D在AB上,________.
(2)如图2猜想与的面积有何关系?请说明理由.(温馨提示:两三角形可以看成是等底的)
20.(12分)如图,在四边形ABCD中,,点E是BC的中点,DE平分.
(1)求证:AE平分.
(2)判断AB,CD,AD之间的数量关系,并证明.
(3)已知,,求.
21.(12分)在中,,点D是线段CB上的一动点(不与点B,C重合),以AD为一边在AD的右侧作,使,,连接CE.
(1)如图(1),当点D在线段CB上,时,_________°.
(2)设,.如图(2),当点D在线段CB上,时,请你探究与之间的数量关系,并证明你的结论.
答案以及解析
1.答案:B
解析:,,,,,应该补充“,”.
2.答案:C
解析:如图,,,,,.,.
3.答案:B
解析:在和中,,,.又,,,.
4.答案:A
解析:,,,,故B选项正确.,,,,故C选项正确.,,,即,故D选项正确.故选A.
5.答案:A
解析:点O为、的中点,
,,
由对顶角相等得,
在和中,
,
,
,
即只要量出的长度,就可以知道该零件内径AB的长度,故选A.
6.答案:B
解析:,,
当时,则,依据SAS即可得到;
当时,则和全等条件是SSA,不能判定;
当时,由于,则,依据ASA即可得到;
当时,则,依据SAS即可得到;
故选B.
7.答案:B
解析:,,
,
,
,
,
,
在和中,
,
,
,,
,故选B.
8.答案:B
解析:,
,,
,
由三角形内角和为可知:,
,故选B.
9.答案:D
解析:平分,平分,,,,故选项C不合题意.在和中,,,,.同理可得,,,,点O是CD的中点,故选项A,B不合题意.故选D.
10.答案:C
解析:过D点作于H,如图,
AD是的角平分线,,,
,
,
,
,,
,
BC平分,所以①正确;
的度数不确定,
而,
不一定等于,
EF与AB不一定平行,所以②错误;
,
,
BD平分,
,
,
,
AD平分,
,所以③正确;
在和中,
,
,
,
在和中,
,
,
,
,
,
,所以④正确.故选C.
11.答案:
解析:在与中,,,.
12.答案:
解析:由题意得:,,,
所以,
,
所以.
13.答案:3
解析:,于D,,.,
.在和中,
,,.,且,,解得.
14.答案:3或
解析:设点P运动的时间为,则,,由,可分以下两种情况讨论.①当,时,,此时,解得,所以,此时点Q的运动速度为.②当,时,,此时,解得,此时点Q的运动速度为.
15.答案:①②④⑤
解析:,AD平分,,
,故①正确;
在和中,,
,
,,
DA平分,故②正确;
,故④正确;
,
,
,故⑤正确;
,而,
,
DE平分错误,故③错误;
综上所述,正确的有①②④⑤.
16.解析:证明:,,
.
在和中,
,
,
,
,
,
.
17.解析:(1),,
.
,.
(2),,
.
,,
.
18.解析:(1)证明:由题意得,,,
,,
.
在和中,
.
(2)由题意知,每块砌墙砖的厚度均为,
,..
由(1)得,
,,
,解得.
答:每块砌墙砖的厚度均为.
19.解析:(1),
,,
,,
,
,
,
故答案为:;
(2).
理由如下:作于F,作交EC的延长线于F,
,
,
,,
,,
,
在和中,
,
,
,
,
,
,,
.
20.解析:(1)证明:如图,过点E作于点F,
,平分,
.
E是BC的中点,
,
.
又,,
平分.
(2).
证明:,
在和中,
,.
同理可得,
.
,.
(3),点E是BC的中点,,.
,.
21.解析:(1),,
.
在和中,
,.
,.
(2).
证明:,
,
.
在和中,
,
.
,
,
.
1
