第二十三章 旋转(测基础)(含解析)——2023-2024学年人教版数学九年级上册单元闯关双测卷
文档属性
| 名称 | 第二十三章 旋转(测基础)(含解析)——2023-2024学年人教版数学九年级上册单元闯关双测卷 |  | |
| 格式 | docx | ||
| 文件大小 | 883.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 22:06:55 | ||
图片预览



文档简介
第二十三章 旋转(测基础)——2023-2024学年人教版数学九年级上册单元闯关双测卷
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.下列图形中既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
2.点关于原点的对称点的坐标是( )
A. B. C. D.
3.下列说法正确的是( )
A.平移不改变图形的形状和大小,而旋转改变图形的形状和大小
B.在成中心对称的两个图形中,连接对称点的线段都被对称中心平分
C.在平面直角坐标系中,一点向右平移2个单位,纵坐标加2
D.在平移和旋转图形中,对应角相等,对应线段相等且平行
4.如图,在中,,,将绕点C旋转得,使得点A,,B在同一条直线上,则旋转的角度是( )
A. B. C. D.
5.如图所示,在平面直角坐标系内,原点O恰好是平行四边形对角线的交点.若点A的坐标为,则点C的坐标为( )
A. B. C. D.
6.如图,在平面直角坐标系中,,,,请确定一点D,使得以点A,B,C,D为顶点的四边形是轴对称图形但不是中心对称图形,则点D的坐标可能是( )
A. B. C. D.
7.将点向右平移2个单位长度得到点,点与点关于y轴对称,点与点关于x轴对称,则点与的关系是( )
A.重合 B.关于y轴对称 C.关于x轴对称 D.关于原点对称
8.如图,底边长为2的等腰的边OB在x轴上,将绕原点O逆时针旋转得到,则点的坐标为( )
A. B. C. D.
9.如图,将绕点旋转得到,设点的坐标为,则点的坐标为( )
A. B. C. D.
10.如图,已知中,,,将绕点A顺时针方向旋转到的位置,连接,则的长为( )
A. B. C. D.1
二、填空题(每小题4分,共20分)
11.如图,与关于点O成中心对称,ED是的中位线,是的中位线,已知,则__________.
12.在平面直角坐标系中,点与点关于原点对称,且点在第三象限,则m的取值范围是___________.
13.如图,在中,,将绕点A顺时针旋转得到,连接,当点B的对应点落在AC边上时,的度数为____.
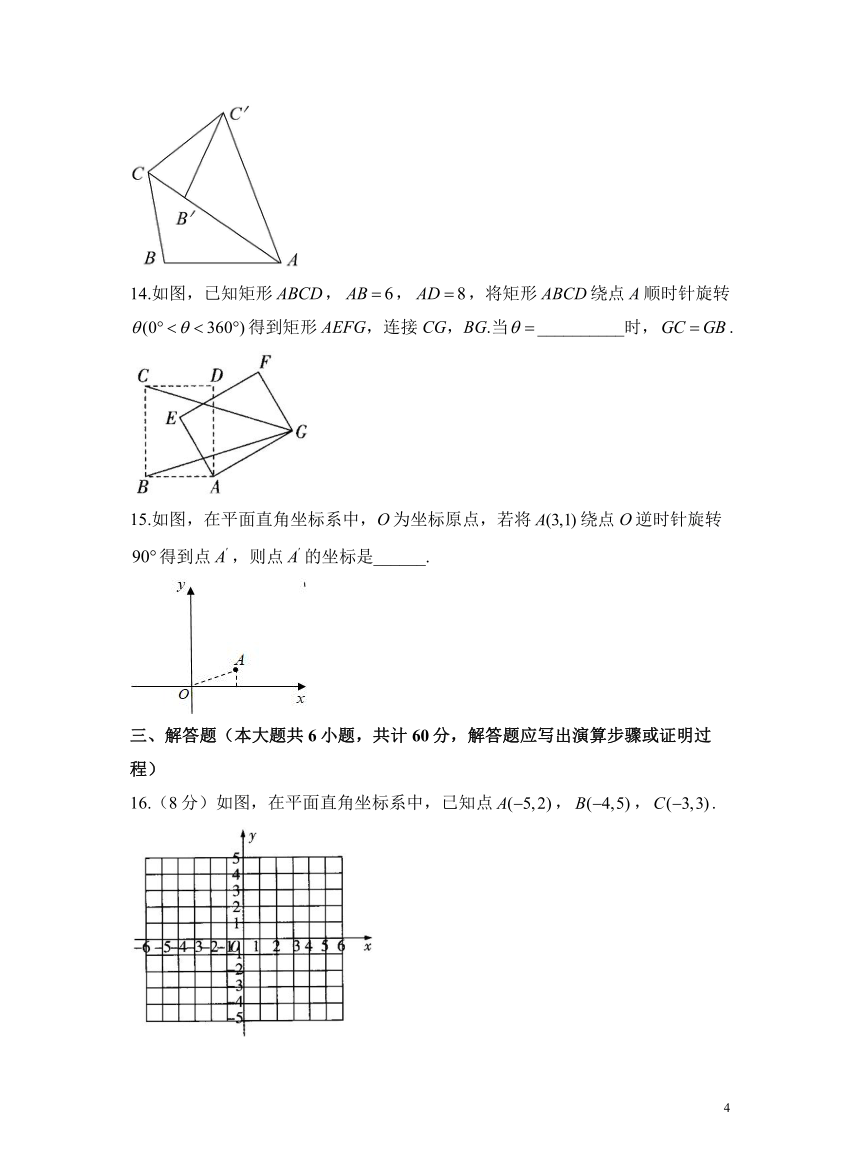
14.如图,已知矩形,,,将矩形ABCD绕点A顺时针旋转得到矩形AEFG,连接CG,BG.当__________时,.
15.如图,在平面直角坐标系中,O为坐标原点,若将绕点O逆时针旋转得到点,则点的坐标是______.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
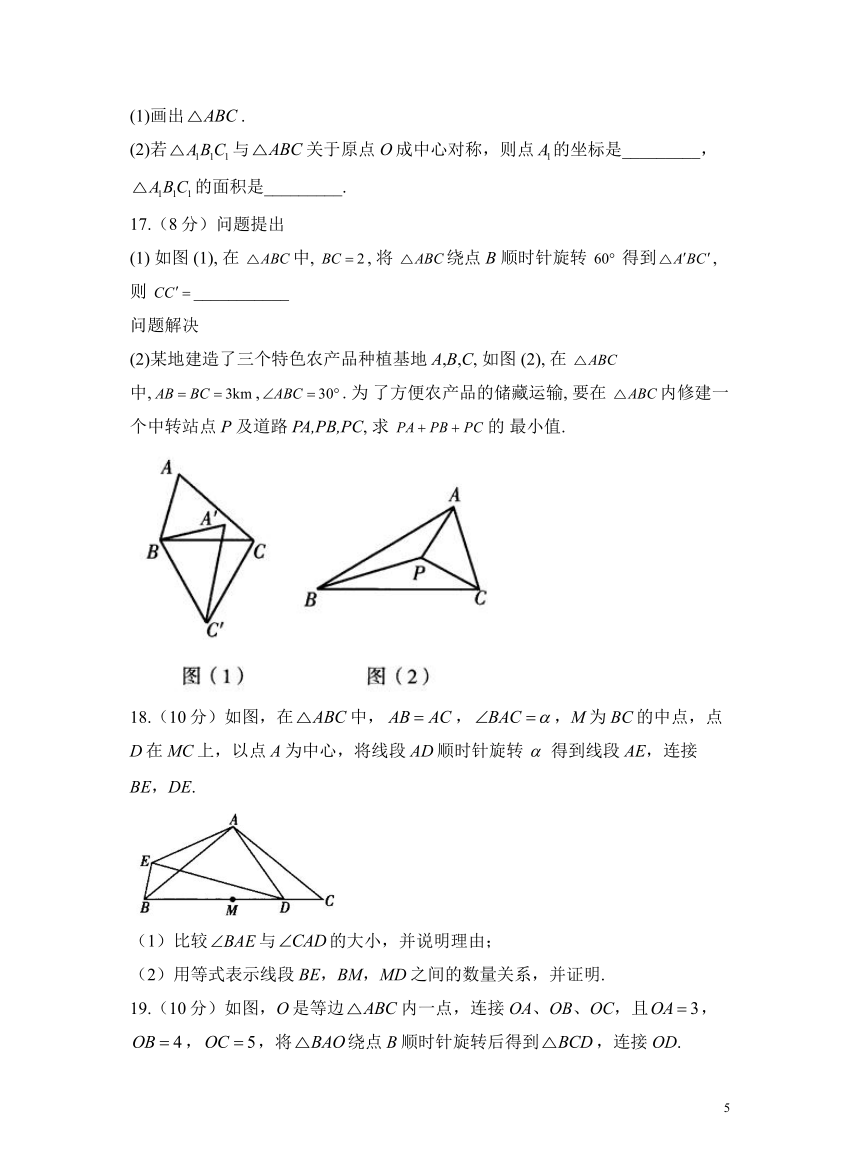
16.(8分)如图,在平面直角坐标系中,已知点,,.
(1)画出.
(2)若与关于原点O成中心对称,则点的坐标是_________,的面积是_________.
17.(8分)问题提出
(1) 如图 (1), 在 中, , 将 绕点B 顺时针旋转 得到, 则 ___________
问题解决
(2)某地建造了三个特色农产品种植基地A,B,C, 如图 (2), 在 中,,. 为 了方便农产品的储藏运输, 要在 内修建一个中转站点P 及道路PA,PB,PC, 求 的 最小值.
18.(10分)如图,在中,,,M为BC的中点,点D在MC上,以点A为中心,将线段AD顺时针旋转得到线段AE,连接BE,DE.
(1)比较与的大小,并说明理由;
(2)用等式表示线段BE,BM,MD之间的数量关系,并证明.
19.(10分)如图,O是等边内一点,连接OA、OB、OC,且,,,将绕点B顺时针旋转后得到,连接OD.
(1)求线段OD的长;
(2)求的度数.
20.(12分)如图,已知线段BC绕某定点O顺时针旋转得到线段EF,其中点B的对应点是点E.
(1)请确定点O的位置;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的情况下,点A位于BC上方,点D位于EF右侧,且,均为等边三角形.求证:可由绕点O顺时针旋转得到.
21.(12分)在中,,是直角三角形,且.将绕点A逆时针旋转一定角度得到,其中点D的对应点是点G,连接并延长交于点H,连接.
(1)如图1,当点D在边上时,求证;
(2)如图2,当点D在内部时,直接写出的大小,并证明.
答案以及解析
1.答案:C
解析:A、不是中心对称图形,是轴对称图形,故此选项错误;
B、不是中心对称图形,是轴对称图形,故此选项错误;
C、是中心对称图形,是轴对称图形,故此选项正确;
D、是中心对称图形,不是轴对称图形,故此选项错误;故选C.
2.答案:B
解析:点关于原点对称,
点关于原点对称的点的坐标为.故选B.
3.答案:B
解析:平移不改变图形的形状和大小,旋转也不改变图形的形状和大小;在成中心对称的两个图形中,连接对称点的线段都被对称中心平分;在平面直角坐标系中,一点向右平移2个单位,横坐标加2;在平移中,对应角相等,对应线段相等且平行(或共线),旋转中对应线段有可能不平行.故选B.
4.答案:C
解析:将绕点C旋转得,,.
,,,.
5.答案:C
解析:已知原点O恰好是平行四边形对角线的交点,可得点C与点A关于原点对称,又因为关于原点对称的两个点的横纵坐标互为相反数,点A的坐标为,所以点C的坐标为.故选C.
6.答案:C
解析:A.若点D的坐标为,则四边形ABDC是正方形,既是轴对称图形,也是轴对称图形,故此选项不符合题意;
B.若点D的坐标为,点A,点D,点C在同一条直线上,故此选项不符合题意;
C.若点D的坐标为,则四边形ABDC是轴对称图形,但不是中心对称图形,故此选项符合题意;
D.若点D坐标为,则四边形ADBC既不是轴对称图形,也不是中心对称图形,故此选项不符合题意.故选C.
7.答案:D
解析:将点向右平移2个单位长度得到点,
由与点关于y轴对称,得,
由点与点关于x轴对称,得,
从而与关于原点对称,故选D.
8.答案:B
解析:交x轴于H,如图,
为等腰直角三角形,
,
绕原点O逆时针旋转得到,
,,,
,
,
,
点的坐标为.故选B.
9.答案:D
解析:根据题意,知点关于点对称,设点的坐标是,由,得,解得,点的坐标是.故选D.
10.答案:C
解析:如图,连接,延长交于点M;
由题意得:,,为等边三角形,,;在与中,,,,且
由题意得:,,,,
由勾股定理得:,,
故选C.
11.答案:2
解析: 与关于点O成中心对称,是的中位线,.
12.答案:
解析:因为在平面直角坐标系中,点与点关于原点对称,且点在第三象限,所以解得.
13.答案:72
解析:将绕点A顺时针旋转得到,
,
,
故答案为:72.
14.答案:或
解析:当时,点G在BC的垂直平分线上.分两种情况讨论:
①如图(1),当点G在AD右侧时,取BC的中点H,连接GH交AD于M,连接.
,,四边形ABHM是矩形,,
垂直平分,,是等边三角形,,旋转角;
②如图(2),当点G在AD左侧时,同理可得,旋转角.
故答案为或.
15.答案:
解析:如图所示,过点A作轴于B,轴于C,
则由旋转的性质可得,,,
,
,,
又在第二象限
故答案为:.
16.答案:(1)图见解析
(2);
解析:(1)如图,为所作.
(2)与关于原点O成中心对称,
点的坐标是,的面积的面积
.
17.答案: (1)2
(2)
解析:(1)略
(2) 如图,
将 绕点B 顺时针旋 转, 得到, 连接,. 由旋转的性质可知 ,,,,,
是等边三角形,,
,
是等腰直角三角形,
在中, 由勾股定理得,
当点 共线时, 的值最小, 最 小值为线段 的长,
的最小值为.
18.答案:(1)
(2)
解析:(1).
理由:由旋转可知,,
,
即.
(2).
证明:,,,
,
.
M是BC的中点,
.
19.答案:(1)4
(2)150°
解析:(1)绕点B顺时针旋转后得到,
,
而,
为等边三角形,
;
(2)为等边三角形,
,,
绕点B顺时针旋转后得到,
,
在中,,,,
,
为直角三角形,,
.
20.解析:(1)如图(1)所示,点O即为所求作的旋转中心.
(2)证明:如图(2),连接OA,OB,OC,OD,OE,OF.
线段BC绕点O旋转得到线段EF,点B的对应点是点E,
,,,,
,
.
,都是等边三角形,
,,,
,,
,
,
,,
,
,
将点A绕点O顺时针旋转到点D,
可由绕点O顺时针旋转得到.
21.解析:(1)如图1,在上截取,
,
,
把绕点A逆时针旋转一定角度得到,
,,,
,,
,
在和中,
,
,
,,
,,
,
,
;
(2)如图2,在上截取,
同(1)可证,
,
,
.
1
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.下列图形中既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
2.点关于原点的对称点的坐标是( )
A. B. C. D.
3.下列说法正确的是( )
A.平移不改变图形的形状和大小,而旋转改变图形的形状和大小
B.在成中心对称的两个图形中,连接对称点的线段都被对称中心平分
C.在平面直角坐标系中,一点向右平移2个单位,纵坐标加2
D.在平移和旋转图形中,对应角相等,对应线段相等且平行
4.如图,在中,,,将绕点C旋转得,使得点A,,B在同一条直线上,则旋转的角度是( )
A. B. C. D.
5.如图所示,在平面直角坐标系内,原点O恰好是平行四边形对角线的交点.若点A的坐标为,则点C的坐标为( )
A. B. C. D.
6.如图,在平面直角坐标系中,,,,请确定一点D,使得以点A,B,C,D为顶点的四边形是轴对称图形但不是中心对称图形,则点D的坐标可能是( )
A. B. C. D.
7.将点向右平移2个单位长度得到点,点与点关于y轴对称,点与点关于x轴对称,则点与的关系是( )
A.重合 B.关于y轴对称 C.关于x轴对称 D.关于原点对称
8.如图,底边长为2的等腰的边OB在x轴上,将绕原点O逆时针旋转得到,则点的坐标为( )
A. B. C. D.
9.如图,将绕点旋转得到,设点的坐标为,则点的坐标为( )
A. B. C. D.
10.如图,已知中,,,将绕点A顺时针方向旋转到的位置,连接,则的长为( )
A. B. C. D.1
二、填空题(每小题4分,共20分)
11.如图,与关于点O成中心对称,ED是的中位线,是的中位线,已知,则__________.
12.在平面直角坐标系中,点与点关于原点对称,且点在第三象限,则m的取值范围是___________.
13.如图,在中,,将绕点A顺时针旋转得到,连接,当点B的对应点落在AC边上时,的度数为____.
14.如图,已知矩形,,,将矩形ABCD绕点A顺时针旋转得到矩形AEFG,连接CG,BG.当__________时,.
15.如图,在平面直角坐标系中,O为坐标原点,若将绕点O逆时针旋转得到点,则点的坐标是______.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,在平面直角坐标系中,已知点,,.
(1)画出.
(2)若与关于原点O成中心对称,则点的坐标是_________,的面积是_________.
17.(8分)问题提出
(1) 如图 (1), 在 中, , 将 绕点B 顺时针旋转 得到, 则 ___________
问题解决
(2)某地建造了三个特色农产品种植基地A,B,C, 如图 (2), 在 中,,. 为 了方便农产品的储藏运输, 要在 内修建一个中转站点P 及道路PA,PB,PC, 求 的 最小值.
18.(10分)如图,在中,,,M为BC的中点,点D在MC上,以点A为中心,将线段AD顺时针旋转得到线段AE,连接BE,DE.
(1)比较与的大小,并说明理由;
(2)用等式表示线段BE,BM,MD之间的数量关系,并证明.
19.(10分)如图,O是等边内一点,连接OA、OB、OC,且,,,将绕点B顺时针旋转后得到,连接OD.
(1)求线段OD的长;
(2)求的度数.
20.(12分)如图,已知线段BC绕某定点O顺时针旋转得到线段EF,其中点B的对应点是点E.
(1)请确定点O的位置;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的情况下,点A位于BC上方,点D位于EF右侧,且,均为等边三角形.求证:可由绕点O顺时针旋转得到.
21.(12分)在中,,是直角三角形,且.将绕点A逆时针旋转一定角度得到,其中点D的对应点是点G,连接并延长交于点H,连接.
(1)如图1,当点D在边上时,求证;
(2)如图2,当点D在内部时,直接写出的大小,并证明.
答案以及解析
1.答案:C
解析:A、不是中心对称图形,是轴对称图形,故此选项错误;
B、不是中心对称图形,是轴对称图形,故此选项错误;
C、是中心对称图形,是轴对称图形,故此选项正确;
D、是中心对称图形,不是轴对称图形,故此选项错误;故选C.
2.答案:B
解析:点关于原点对称,
点关于原点对称的点的坐标为.故选B.
3.答案:B
解析:平移不改变图形的形状和大小,旋转也不改变图形的形状和大小;在成中心对称的两个图形中,连接对称点的线段都被对称中心平分;在平面直角坐标系中,一点向右平移2个单位,横坐标加2;在平移中,对应角相等,对应线段相等且平行(或共线),旋转中对应线段有可能不平行.故选B.
4.答案:C
解析:将绕点C旋转得,,.
,,,.
5.答案:C
解析:已知原点O恰好是平行四边形对角线的交点,可得点C与点A关于原点对称,又因为关于原点对称的两个点的横纵坐标互为相反数,点A的坐标为,所以点C的坐标为.故选C.
6.答案:C
解析:A.若点D的坐标为,则四边形ABDC是正方形,既是轴对称图形,也是轴对称图形,故此选项不符合题意;
B.若点D的坐标为,点A,点D,点C在同一条直线上,故此选项不符合题意;
C.若点D的坐标为,则四边形ABDC是轴对称图形,但不是中心对称图形,故此选项符合题意;
D.若点D坐标为,则四边形ADBC既不是轴对称图形,也不是中心对称图形,故此选项不符合题意.故选C.
7.答案:D
解析:将点向右平移2个单位长度得到点,
由与点关于y轴对称,得,
由点与点关于x轴对称,得,
从而与关于原点对称,故选D.
8.答案:B
解析:交x轴于H,如图,
为等腰直角三角形,
,
绕原点O逆时针旋转得到,
,,,
,
,
,
点的坐标为.故选B.
9.答案:D
解析:根据题意,知点关于点对称,设点的坐标是,由,得,解得,点的坐标是.故选D.
10.答案:C
解析:如图,连接,延长交于点M;
由题意得:,,为等边三角形,,;在与中,,,,且
由题意得:,,,,
由勾股定理得:,,
故选C.
11.答案:2
解析: 与关于点O成中心对称,是的中位线,.
12.答案:
解析:因为在平面直角坐标系中,点与点关于原点对称,且点在第三象限,所以解得.
13.答案:72
解析:将绕点A顺时针旋转得到,
,
,
故答案为:72.
14.答案:或
解析:当时,点G在BC的垂直平分线上.分两种情况讨论:
①如图(1),当点G在AD右侧时,取BC的中点H,连接GH交AD于M,连接.
,,四边形ABHM是矩形,,
垂直平分,,是等边三角形,,旋转角;
②如图(2),当点G在AD左侧时,同理可得,旋转角.
故答案为或.
15.答案:
解析:如图所示,过点A作轴于B,轴于C,
则由旋转的性质可得,,,
,
,,
又在第二象限
故答案为:.
16.答案:(1)图见解析
(2);
解析:(1)如图,为所作.
(2)与关于原点O成中心对称,
点的坐标是,的面积的面积
.
17.答案: (1)2
(2)
解析:(1)略
(2) 如图,
将 绕点B 顺时针旋 转, 得到, 连接,. 由旋转的性质可知 ,,,,,
是等边三角形,,
,
是等腰直角三角形,
在中, 由勾股定理得,
当点 共线时, 的值最小, 最 小值为线段 的长,
的最小值为.
18.答案:(1)
(2)
解析:(1).
理由:由旋转可知,,
,
即.
(2).
证明:,,,
,
.
M是BC的中点,
.
19.答案:(1)4
(2)150°
解析:(1)绕点B顺时针旋转后得到,
,
而,
为等边三角形,
;
(2)为等边三角形,
,,
绕点B顺时针旋转后得到,
,
在中,,,,
,
为直角三角形,,
.
20.解析:(1)如图(1)所示,点O即为所求作的旋转中心.
(2)证明:如图(2),连接OA,OB,OC,OD,OE,OF.
线段BC绕点O旋转得到线段EF,点B的对应点是点E,
,,,,
,
.
,都是等边三角形,
,,,
,,
,
,
,,
,
,
将点A绕点O顺时针旋转到点D,
可由绕点O顺时针旋转得到.
21.解析:(1)如图1,在上截取,
,
,
把绕点A逆时针旋转一定角度得到,
,,,
,,
,
在和中,
,
,
,,
,,
,
,
;
(2)如图2,在上截取,
同(1)可证,
,
,
.
1
同课章节目录
