第二十三章 旋转(测能力)(含解析)——2023-2024学年人教版数学九年级上册单元闯关双测卷
文档属性
| 名称 | 第二十三章 旋转(测能力)(含解析)——2023-2024学年人教版数学九年级上册单元闯关双测卷 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 00:00:00 | ||
图片预览



文档简介
第二十三章 旋转(测能力)——2023-2024学年人教版数学九年级上册单元闯关双测卷
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.2022年4月16日,神舟十三号载人飞船圆满完成全部既定任务,顺利返回地球家园.六个月的飞天之旅展现了中国航天科技的新高度.下列航天图标,其文字上方的图案是中心对称图形的是( )
A.中国探火 B.中国火箭
C.中国行星探测 D.航天神舟
2.已知点与点关于原点对称, 则的值为( )
A. -1 B. 0 C. 1 D. 4045
3.如图,与关于点O成中心对称,下列结论中不成立的是( )
A. B.
C.点A的对称点是点 D.
4.如图, 在中,,,将绕点C顺时针旋转至, 点A的对应点恰好落在上, 则的长为( )
A. B. C. 2 D.
5.已知点与点关于原点对称,则的值是( )
A.2 B. C.4 D.8
6.如图,将线段AB绕点O顺时针旋转得到线段,那么的对应点的坐标是( )
A. B. C. D.
7.如图,已知点A与点C关于点O对称,点B与点D也关于点O对称,若,,则AB的长可能是( )
A.3 B.4 C.7 D.11
8.如图,在平面直角坐标系中,的一条直角边OB在x轴上,点A的坐标为中,,,连接BC,点M是BC中点,连接AM.将以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是( )
A.3 B. C. D.2
9.已知正方形的对称中心在坐标原点,顶点按逆时针依次排列,若点的坐标为,则点与点的坐标分别为( )
A. B.
C. D.
10.如图,已知中,,,将绕A点逆时针旋转50°得到,以下结论:①,②,③,④,正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题(每小题4分,共20分)
11.已知点与点关于原点对称,则______.
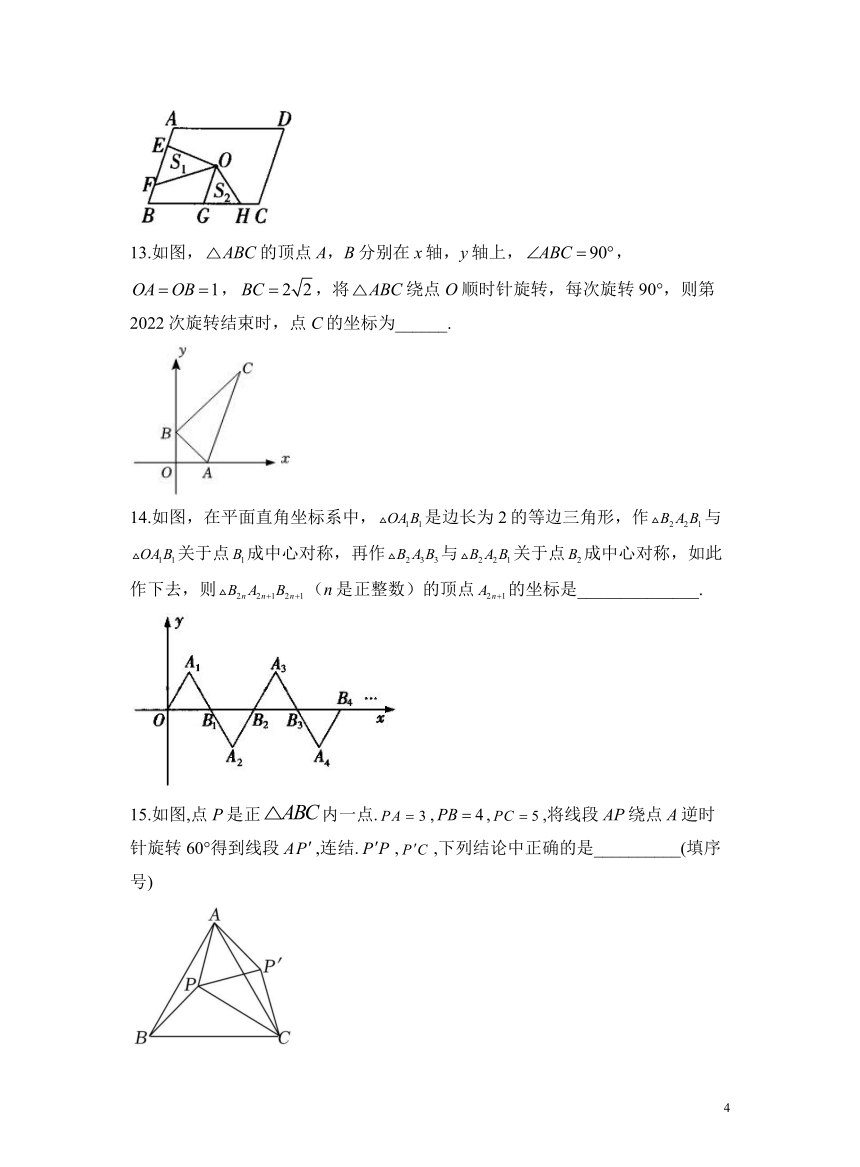
12.如图,点O是的对称中心, 是边上的点,且是边上的点,且.若分别表示和
的面积,则与之间的等量关系是___________.
13.如图,的顶点A,B分别在x轴,y轴上,,,,将绕点O顺时针旋转,每次旋转90°,则第2022次旋转结束时,点C的坐标为______.
14.如图,在平面直角坐标系中,是边长为2的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,如此作下去,则(n是正整数)的顶点的坐标是______________.
15.如图,点P是正内一点.,,,将线段AP绕点A逆时针旋转60°得到线段,连结.,,下列结论中正确的是__________(填序号)
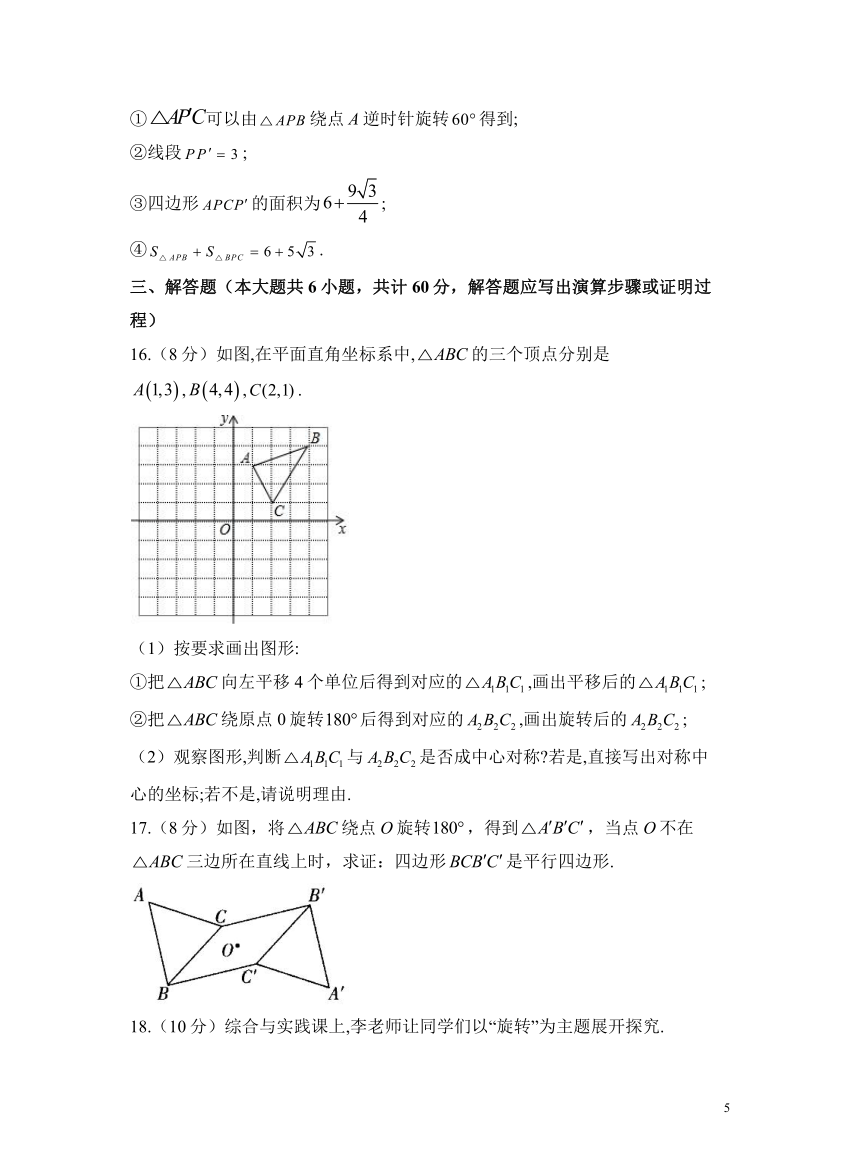
①可以由绕点A逆时针旋转得到;
②线段;
③四边形的面积为;
④.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,在平面直角坐标系中,的三个顶点分别是,,.
(1)按要求画出图形:
①把向左平移4个单位后得到对应的,画出平移后的;
②把绕原点0旋转后得到对应的,画出旋转后的;
(2)观察图形,判断与是否成中心对称 若是,直接写出对称中
心的坐标;若不是,请说明理由.
17.(8分)如图,将绕点O旋转,得到,当点O不在三边所在直线上时,求证:四边形是平行四边形.
18.(10分)综合与实践课上,李老师让同学们以“旋转”为主题展开探究.
【问题情境】
如图①,在矩形ABCD中,,.将边AB绕点A逆时针旋转得到线段AE,过点E作交直线BC与点F.
【猜想证明】
(1)当时,四边形ABFE的形状为______;(直接写出答案)
(2)如图②,当时,连接DE,求此时的面积;
【能力提升】
(3)在【问题情境】的条件下,是否存,使点F,E,D三点共线 若存在,请直接写出此时BF的长度;若不存在,请说明理由.
19.(10分)如图,AC是矩形ABCD的对角线.把绕点A顺时针旋转一定角度得到,点C的对应点F落在CD的延长线上.求证:
(1);
(2)B,D,E三点在同一条直线上.
20.(12分)(1)感知:
如图1,在等腰三角形ABC中,,,将边AB绕点B顺时针旋转得到线段BD,过点D作交CB的延长线于点E,连接CD.
则线段BC与DE的数量关系是______,的面积为______(用含x的式子表示);
(2)应用:
如图2,在一般的中,,,将边AB绕点B顺时针旋转得到线段BD,连接CD,用含x的式子表示的面积,并说明理由.
(3)拓展:
如图3所示,在等腰三角形ABC中,,将边AB绕点B顺时针旋转,当,连接CD,若的面积为9,则CD的长为______.
21.(12分)在正方形ABCD的边AB上任取一点E,作交BD于点F,取FD的中点G,连接EG,CG,如图①,易证且.
(1)将绕点B逆时针旋转,如图②,则线段EG和CG有怎样的数量关系和位置关系 请直接写出你的猜想.
(2)将绕点B逆时针旋转,如图③,则线段EG和CG又有怎样的数量关系和位置关系 请写出你的猜想,并加以证明.
答案以及解析
1.答案:B
解析:选项A、C、D均不能找到这样的一个点,使图形绕某一点旋转180度后和原图形完全重合,所以不是中心对称图形,
选项B能找到这样的一个点,使图形绕某一点旋转180度后和原图形完全重合,所以是中心对称图形,故选B.
2.答案:C
解析:点 与点 关于 原点对称, ,,
.
3.答案:B
解析:与关于点O成中心对称,,,点A的对称点是点,,故A,C,D正确.
4.答案:B
解析:将 绕点C顺时针旋转 至 ,
,
和 均为等边三角形,
,
点 在上, ,
,
在中,,
.
5.答案:B
解析:点与点关于原点对称,
解得:
则.
故选B.
6.答案:B
解析:线段AB绕点O顺时针旋转得到线段,
,,
.
作轴于C,轴于,
.
,
,
.
在和中,
,
,
,.
,
,,
,,
.
故选:B.
7.答案:C
解析:如图,连接CD,
点A与点C关于点O对称,点B与点D也关于点O对称,
,,
四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形),
,
,
,,
在中,,根据“三角形两边之和大于第三边,三角形两边之差小于第三边”可得:
,
,
,
,
3,4,11不符合,7符合;
选项A,B,D错误,选项C正确.
故选:C.
8.答案:A
解析:取OB中点
N,连接MN,AN.
在 中,,
,
M,N分别是BC、OB的中点,
,
在中,,
,
在中,;
当M运动到AN上时,,
,
线段AM的最小值是3,
故选: A.
9.答案:B
解析:如图所示,连接,作轴,轴,四边形为正方形,为对称中心,,,.点与点关于原点对称,,故选B.
10.答案:B
解析:①绕A点逆时针旋转50°得到,.故①正确;②绕A点逆时针旋转50°,.,.,.,.故②正确;③在中,,,..与不垂直.故③不正确;④在中,,,..故④正确.①②④这三个结论正确.故选:B.
11.答案:-1
解析:点与点关于原点对称,
,,
.
故答案为:-1.
12.答案:
解析:,点O是的对称中心,.
13.答案:
解析:由题意,
第一次旋转得到的坐标为,
第二次旋转得到的坐标为,
第三次旋转得到的坐标为,
第四次旋转得到的坐标为,
…
四次一个循环,
,
则第2022次旋转结束时,点C的坐标为,
故答案为:.
14.答案:
解析:是边长为2的等边三角形,点的坐标为,点的坐标为,点与点关于点成中心对称,点的坐标是,点与点关于点成中心对称,点的坐标是,点与点关于点成中心对称,点的坐标是,依此类推,可得点的横坐标是,点的横坐标是,当n为奇数时,点的纵坐标是,当n为偶数时,点的纵坐标是,点的坐标是.
15.答案:①②③
解析:为等边三角形,
,,
线段AP绕点A逆时针旋转
得到线段,
,,
为等边三角形,
,,所以②正确;
,
即,
在和中,
,
可以由绕点A逆时针旋转
得到,所以①正确;
,,,
在中,,,,
,
为直角三角形,,
四边形的面积,所以③正确;
把绕B点顺时针旋转得到,连接PD,如图,
,,,,
为等边三角形,
,
,,,
,
为直角三角形,,
,所以④错误.
故答案为:①②③.
16.解析:(1)如图
(2)连接,,,相交于点,
则点即为与的对称中心.
17.解析:证明:如图,连接,,
B点绕O点旋转到,
,点B,O,三点共线.
C点绕O点旋转到,
,点C,O,三点共线.
四边形是平行四边形.
18.解析:(1)正方形;
(2)如图,过点E作交AD与点H,
,
,,
,且,
设,在中,,
.
,
(3)或
19.解析:(1)证明:由旋转的性质可得,,,
.
,,
,
.
(2)证法一:如图,连接BE,BD,设BD交AC于点O.
由旋转可知,,,
.
四边形ABCD是矩形,,,
,,
,,
B,E,D三点在同一直线上.
证法二:如图,连接DE,BE.
,
点A,F,D,E在以AF为直径的圆上,
.
由旋转可知,,,
,
,
B,E,D三点在同一条直线上.
20.答案:(1);;
(2),理由见解析;
(3);
解析:(1)由题意得:,
,
,
故答案是:,;
(2)如图1,
,理由如下:
作于E,
,
,
,
,
,
在和中,
,
,
,
;
(3)如图2,
作于F,作于E,
由(2)知:,
,,
,
,
,
,
,
,,
在中,,,
.
21.解析:(1),
(2),
证明如下:延长FE交DC的延长线于点M,连接MG,如图所示
易得,,
四边形BEMC是矩形
,,.
易知,,
又,
为等腰直角三角形
,,
,
,,
,,
,
,
,
又,
,
,
在和中,
,
,
,,
,,
,,
即,
1
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.2022年4月16日,神舟十三号载人飞船圆满完成全部既定任务,顺利返回地球家园.六个月的飞天之旅展现了中国航天科技的新高度.下列航天图标,其文字上方的图案是中心对称图形的是( )
A.中国探火 B.中国火箭
C.中国行星探测 D.航天神舟
2.已知点与点关于原点对称, 则的值为( )
A. -1 B. 0 C. 1 D. 4045
3.如图,与关于点O成中心对称,下列结论中不成立的是( )
A. B.
C.点A的对称点是点 D.
4.如图, 在中,,,将绕点C顺时针旋转至, 点A的对应点恰好落在上, 则的长为( )
A. B. C. 2 D.
5.已知点与点关于原点对称,则的值是( )
A.2 B. C.4 D.8
6.如图,将线段AB绕点O顺时针旋转得到线段,那么的对应点的坐标是( )
A. B. C. D.
7.如图,已知点A与点C关于点O对称,点B与点D也关于点O对称,若,,则AB的长可能是( )
A.3 B.4 C.7 D.11
8.如图,在平面直角坐标系中,的一条直角边OB在x轴上,点A的坐标为中,,,连接BC,点M是BC中点,连接AM.将以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是( )
A.3 B. C. D.2
9.已知正方形的对称中心在坐标原点,顶点按逆时针依次排列,若点的坐标为,则点与点的坐标分别为( )
A. B.
C. D.
10.如图,已知中,,,将绕A点逆时针旋转50°得到,以下结论:①,②,③,④,正确的有( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题(每小题4分,共20分)
11.已知点与点关于原点对称,则______.
12.如图,点O是的对称中心, 是边上的点,且是边上的点,且.若分别表示和
的面积,则与之间的等量关系是___________.
13.如图,的顶点A,B分别在x轴,y轴上,,,,将绕点O顺时针旋转,每次旋转90°,则第2022次旋转结束时,点C的坐标为______.
14.如图,在平面直角坐标系中,是边长为2的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,如此作下去,则(n是正整数)的顶点的坐标是______________.
15.如图,点P是正内一点.,,,将线段AP绕点A逆时针旋转60°得到线段,连结.,,下列结论中正确的是__________(填序号)
①可以由绕点A逆时针旋转得到;
②线段;
③四边形的面积为;
④.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,在平面直角坐标系中,的三个顶点分别是,,.
(1)按要求画出图形:
①把向左平移4个单位后得到对应的,画出平移后的;
②把绕原点0旋转后得到对应的,画出旋转后的;
(2)观察图形,判断与是否成中心对称 若是,直接写出对称中
心的坐标;若不是,请说明理由.
17.(8分)如图,将绕点O旋转,得到,当点O不在三边所在直线上时,求证:四边形是平行四边形.
18.(10分)综合与实践课上,李老师让同学们以“旋转”为主题展开探究.
【问题情境】
如图①,在矩形ABCD中,,.将边AB绕点A逆时针旋转得到线段AE,过点E作交直线BC与点F.
【猜想证明】
(1)当时,四边形ABFE的形状为______;(直接写出答案)
(2)如图②,当时,连接DE,求此时的面积;
【能力提升】
(3)在【问题情境】的条件下,是否存,使点F,E,D三点共线 若存在,请直接写出此时BF的长度;若不存在,请说明理由.
19.(10分)如图,AC是矩形ABCD的对角线.把绕点A顺时针旋转一定角度得到,点C的对应点F落在CD的延长线上.求证:
(1);
(2)B,D,E三点在同一条直线上.
20.(12分)(1)感知:
如图1,在等腰三角形ABC中,,,将边AB绕点B顺时针旋转得到线段BD,过点D作交CB的延长线于点E,连接CD.
则线段BC与DE的数量关系是______,的面积为______(用含x的式子表示);
(2)应用:
如图2,在一般的中,,,将边AB绕点B顺时针旋转得到线段BD,连接CD,用含x的式子表示的面积,并说明理由.
(3)拓展:
如图3所示,在等腰三角形ABC中,,将边AB绕点B顺时针旋转,当,连接CD,若的面积为9,则CD的长为______.
21.(12分)在正方形ABCD的边AB上任取一点E,作交BD于点F,取FD的中点G,连接EG,CG,如图①,易证且.
(1)将绕点B逆时针旋转,如图②,则线段EG和CG有怎样的数量关系和位置关系 请直接写出你的猜想.
(2)将绕点B逆时针旋转,如图③,则线段EG和CG又有怎样的数量关系和位置关系 请写出你的猜想,并加以证明.
答案以及解析
1.答案:B
解析:选项A、C、D均不能找到这样的一个点,使图形绕某一点旋转180度后和原图形完全重合,所以不是中心对称图形,
选项B能找到这样的一个点,使图形绕某一点旋转180度后和原图形完全重合,所以是中心对称图形,故选B.
2.答案:C
解析:点 与点 关于 原点对称, ,,
.
3.答案:B
解析:与关于点O成中心对称,,,点A的对称点是点,,故A,C,D正确.
4.答案:B
解析:将 绕点C顺时针旋转 至 ,
,
和 均为等边三角形,
,
点 在上, ,
,
在中,,
.
5.答案:B
解析:点与点关于原点对称,
解得:
则.
故选B.
6.答案:B
解析:线段AB绕点O顺时针旋转得到线段,
,,
.
作轴于C,轴于,
.
,
,
.
在和中,
,
,
,.
,
,,
,,
.
故选:B.
7.答案:C
解析:如图,连接CD,
点A与点C关于点O对称,点B与点D也关于点O对称,
,,
四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形),
,
,
,,
在中,,根据“三角形两边之和大于第三边,三角形两边之差小于第三边”可得:
,
,
,
,
3,4,11不符合,7符合;
选项A,B,D错误,选项C正确.
故选:C.
8.答案:A
解析:取OB中点
N,连接MN,AN.
在 中,,
,
M,N分别是BC、OB的中点,
,
在中,,
,
在中,;
当M运动到AN上时,,
,
线段AM的最小值是3,
故选: A.
9.答案:B
解析:如图所示,连接,作轴,轴,四边形为正方形,为对称中心,,,.点与点关于原点对称,,故选B.
10.答案:B
解析:①绕A点逆时针旋转50°得到,.故①正确;②绕A点逆时针旋转50°,.,.,.,.故②正确;③在中,,,..与不垂直.故③不正确;④在中,,,..故④正确.①②④这三个结论正确.故选:B.
11.答案:-1
解析:点与点关于原点对称,
,,
.
故答案为:-1.
12.答案:
解析:,点O是的对称中心,.
13.答案:
解析:由题意,
第一次旋转得到的坐标为,
第二次旋转得到的坐标为,
第三次旋转得到的坐标为,
第四次旋转得到的坐标为,
…
四次一个循环,
,
则第2022次旋转结束时,点C的坐标为,
故答案为:.
14.答案:
解析:是边长为2的等边三角形,点的坐标为,点的坐标为,点与点关于点成中心对称,点的坐标是,点与点关于点成中心对称,点的坐标是,点与点关于点成中心对称,点的坐标是,依此类推,可得点的横坐标是,点的横坐标是,当n为奇数时,点的纵坐标是,当n为偶数时,点的纵坐标是,点的坐标是.
15.答案:①②③
解析:为等边三角形,
,,
线段AP绕点A逆时针旋转
得到线段,
,,
为等边三角形,
,,所以②正确;
,
即,
在和中,
,
可以由绕点A逆时针旋转
得到,所以①正确;
,,,
在中,,,,
,
为直角三角形,,
四边形的面积,所以③正确;
把绕B点顺时针旋转得到,连接PD,如图,
,,,,
为等边三角形,
,
,,,
,
为直角三角形,,
,所以④错误.
故答案为:①②③.
16.解析:(1)如图
(2)连接,,,相交于点,
则点即为与的对称中心.
17.解析:证明:如图,连接,,
B点绕O点旋转到,
,点B,O,三点共线.
C点绕O点旋转到,
,点C,O,三点共线.
四边形是平行四边形.
18.解析:(1)正方形;
(2)如图,过点E作交AD与点H,
,
,,
,且,
设,在中,,
.
,
(3)或
19.解析:(1)证明:由旋转的性质可得,,,
.
,,
,
.
(2)证法一:如图,连接BE,BD,设BD交AC于点O.
由旋转可知,,,
.
四边形ABCD是矩形,,,
,,
,,
B,E,D三点在同一直线上.
证法二:如图,连接DE,BE.
,
点A,F,D,E在以AF为直径的圆上,
.
由旋转可知,,,
,
,
B,E,D三点在同一条直线上.
20.答案:(1);;
(2),理由见解析;
(3);
解析:(1)由题意得:,
,
,
故答案是:,;
(2)如图1,
,理由如下:
作于E,
,
,
,
,
,
在和中,
,
,
,
;
(3)如图2,
作于F,作于E,
由(2)知:,
,,
,
,
,
,
,
,,
在中,,,
.
21.解析:(1),
(2),
证明如下:延长FE交DC的延长线于点M,连接MG,如图所示
易得,,
四边形BEMC是矩形
,,.
易知,,
又,
为等腰直角三角形
,,
,
,,
,,
,
,
,
又,
,
,
在和中,
,
,
,,
,,
,,
即,
1
同课章节目录
