向量的基本概念
图片预览




文档简介
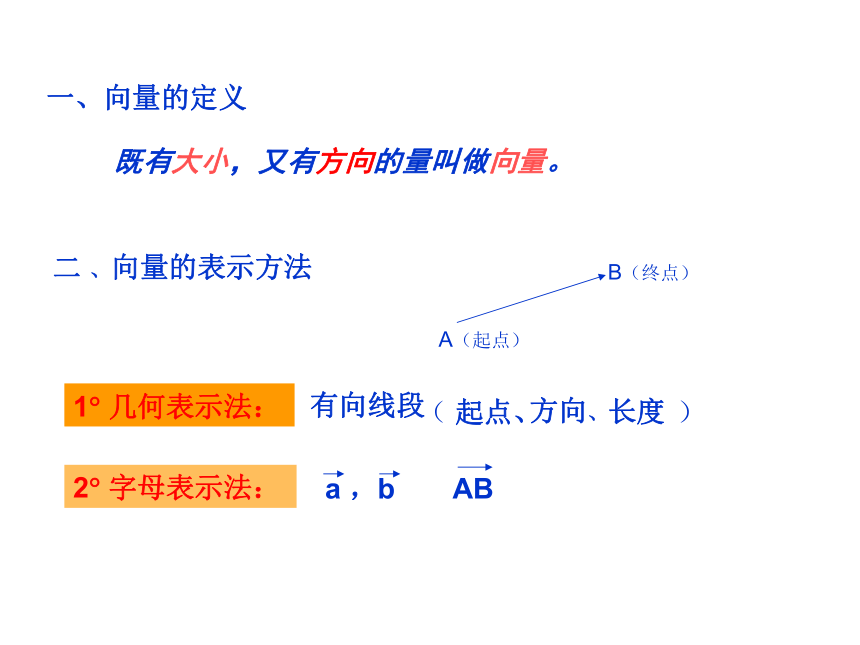
课件14张PPT。2.1向量的基本概念一、向量的定义既有大小,又有方向的量叫做向量。二 、向量的表示方法有向线段 ( 起点、 )1? 几何表示法: 方向、长度单位向量---长度(模)等于1个单位长度的向量叫作单位向量。2.两个特殊向量: 问:在平面上把所有单位向量的起点平移到同一点P,那么它们的终点的集合组成什么图形?三、 向量的有关概念
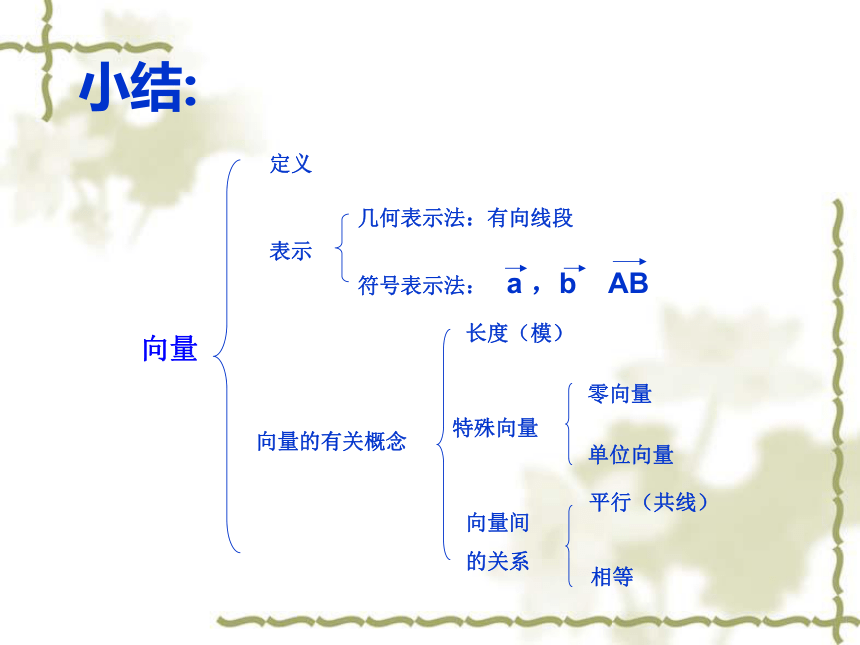
3.向量间的关系 平行向量又叫做共线向量向量相等 向量平行平行向量一定是相等向量吗?向量定义长度(模)表示几何表示法:有向线段符号表示法:零向量单位向量向量间
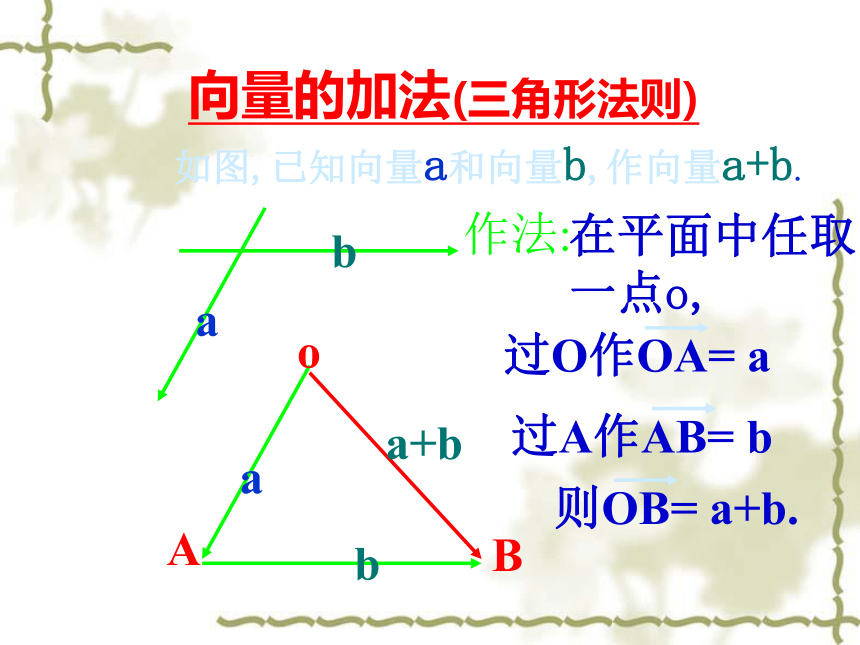
的关系相等平行(共线)向量的有关概念特殊向量小结:向量的加法(三角形法则)如图,已知向量a和向量b,作向量a+b.作法:在平面中任取
一点o,o向量的加法(平行四边形法则)如图,已知向量a和向量b,作向量a+b.作法:在平面中任取一点o,过O作OA= a过O作OB= bb则对角线
OC= a+b向量的数乘
一般地,实数λ与向量a的积是一个向量,
这种运算叫做向量的数乘运算,记作λa,
它的长度和方向规定如下:
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0或a=0时, λa=0
定理:向量 b 与非零向量 a 共线当且仅当
有且只有一个实数λ,使得 b=λa
证明共线就是证明两向量成倍数关系平面向量基本定理 a = + abe1e22.3.3平面向量的坐标运算平面向量的坐标运算两个向量和与差的坐标分别等于这两向量相应坐标的和与差 一个向量的坐标等于表示此向量的有向线段的终点的坐
标减去始点的坐标. 实数与向量的积的坐标等于这个实数乘原来的向量的相
应坐标.平行向量坐标之间的关系
a=(x1,y1), b=(x1,y1)其中b=0,若a,b共线,
则 x1y2-x2y1=0
的关系相等平行(共线)向量的有关概念特殊向量小结:向量的加法(三角形法则)如图,已知向量a和向量b,作向量a+b.作法:在平面中任取
一点o,o向量的加法(平行四边形法则)如图,已知向量a和向量b,作向量a+b.作法:在平面中任取一点o,过O作OA= a过O作OB= bb则对角线
OC= a+b向量的数乘
一般地,实数λ与向量a的积是一个向量,
这种运算叫做向量的数乘运算,记作λa,
它的长度和方向规定如下:
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0或a=0时, λa=0
定理:向量 b 与非零向量 a 共线当且仅当
有且只有一个实数λ,使得 b=λa
证明共线就是证明两向量成倍数关系平面向量基本定理 a = + abe1e22.3.3平面向量的坐标运算平面向量的坐标运算两个向量和与差的坐标分别等于这两向量相应坐标的和与差 一个向量的坐标等于表示此向量的有向线段的终点的坐
标减去始点的坐标. 实数与向量的积的坐标等于这个实数乘原来的向量的相
应坐标.平行向量坐标之间的关系
a=(x1,y1), b=(x1,y1)其中b=0,若a,b共线,
则 x1y2-x2y1=0
