求二次函数最值
图片预览






文档简介
课件18张PPT。句容市天王中学 张映明 二次函数最值1.形如y= (a、b、C是常数,且 )
的函数叫做y关于x的二次函数。
ax2+bx+ca≠02.二次函数y=ax2+bx+c(a≠0)
①开口方向:当a>0时,______,当a<0时,_____;
②顶点坐标是( ___ , ___ );
③对称轴是_____;
④函数的最大值或最小值:
当a>0,x=___时,y有最___值,为y=____;
当a<0,x=____时,y有最__值,为y=____。开口向上开口向下小大1.当K=_____时,y=(k–3)x k2-7 是二次函数。
2.二次函数y=x2+2x-4的图象和方向是______,
顶点坐标是______,对称轴是_____,当x_____
时,y有最____值,是______。 -3向上(-1,-5)X=-1=-1小-5例1. 某商场购进一批单价为16元的日用品,经实
验发现若按每件20元的价格销售时,每月能卖360
件,若按每件25元的价格销售时,每月能卖210件,假
设每月销售件数为y(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的函数关系式.
(2)在商品不积压,且不考虑其他因素的条件下,
问:销售价格定为每件多少时,才能使每月获得最大
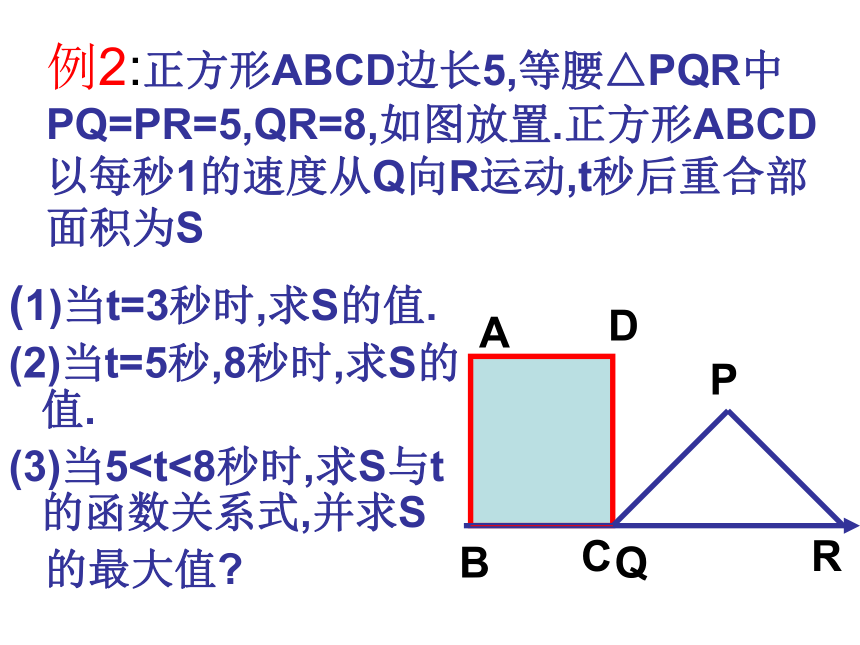
利润?每月的最大利润是多少? 解: (1)设y=kx+b把x=20时,y=360;x=25时,y=210分别代入上式 得 :360=20k+b 210=25k+b 解得:k=-30,b=960 所以y与x之间的函数关系式为y=-30x+960(X≥16,且x为整数)(2)设每月利润为P元,则P=y(x-16)=(-30x+960)(x-16)=-30x2+1440x-15360P为最大值:(-30×24+960)(24-16)=1920(元) 答:当销售价格为每件24元时,每月利润最大,最大利润为1920元。例2:正方形ABCD边长5,等腰△PQR中PQ=PR=5,QR=8,如图放置.正方形ABCD以每秒1的速度从Q向R运动,t秒后重合部面积为S(1)当t=3秒时,求S的值.
(2)当t=5秒,8秒时,求S的值.
(3)当5 的最大值?
ABCDPRQABCDPRQ54E35ABCDPRQ3F9/4ABCDPRQF53ABCDPRQF83ABCDPRQtFG8-tt-53(t-5)/43(8-t)/4
1,已知二次函数y=2x2-4x-3,若-1≤X≤5,求y的最大值和最小值。解: y =2x2-4x-3 =2(x2-2x+1)-5=2(x-1)2-5 顶点坐标为(1,-5)而-1≤x≤5 ∴y最小=-5 ∴y最大=27 思考: 若2≤X≤5 y最小=_____,y最大=_____.-3272. 如图,在ΔABC中,AB=8cm
BC=6cm,∠B=90°,点P从点A开始沿AB边向
点B以2厘米/秒的速度移动,点Q从点B开始沿BC
边向点C以1厘米/秒的速度移动,如果P、Q分别
从A、B同时出发。
(1)几秒后,PQ//AC?
(2)几秒后ΔPBQ的面积最大?
最大面积是多少?PQCBA谈谈你的收获小结:用长8m的铝合金条制成如图的矩形窗框,那么当长、宽分别为多少时,才能使窗框的边的透光面积最大?最大的透光面积是多少2.在矩形荒地ABCD中,AB=10,BC=6,现在四边点分别选取了E、F、G、H四点,且AE=AH=CF=CG=X,建一个花园,如何设计可使花园,面积最大?谢谢!
的函数叫做y关于x的二次函数。
ax2+bx+ca≠02.二次函数y=ax2+bx+c(a≠0)
①开口方向:当a>0时,______,当a<0时,_____;
②顶点坐标是( ___ , ___ );
③对称轴是_____;
④函数的最大值或最小值:
当a>0,x=___时,y有最___值,为y=____;
当a<0,x=____时,y有最__值,为y=____。开口向上开口向下小大1.当K=_____时,y=(k–3)x k2-7 是二次函数。
2.二次函数y=x2+2x-4的图象和方向是______,
顶点坐标是______,对称轴是_____,当x_____
时,y有最____值,是______。 -3向上(-1,-5)X=-1=-1小-5例1. 某商场购进一批单价为16元的日用品,经实
验发现若按每件20元的价格销售时,每月能卖360
件,若按每件25元的价格销售时,每月能卖210件,假
设每月销售件数为y(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的函数关系式.
(2)在商品不积压,且不考虑其他因素的条件下,
问:销售价格定为每件多少时,才能使每月获得最大
利润?每月的最大利润是多少? 解: (1)设y=kx+b把x=20时,y=360;x=25时,y=210分别代入上式 得 :360=20k+b 210=25k+b 解得:k=-30,b=960 所以y与x之间的函数关系式为y=-30x+960(X≥16,且x为整数)(2)设每月利润为P元,则P=y(x-16)=(-30x+960)(x-16)=-30x2+1440x-15360P为最大值:(-30×24+960)(24-16)=1920(元) 答:当销售价格为每件24元时,每月利润最大,最大利润为1920元。例2:正方形ABCD边长5,等腰△PQR中PQ=PR=5,QR=8,如图放置.正方形ABCD以每秒1的速度从Q向R运动,t秒后重合部面积为S(1)当t=3秒时,求S的值.
(2)当t=5秒,8秒时,求S的值.
(3)当5
ABCDPRQABCDPRQ54E35ABCDPRQ3F9/4ABCDPRQF53ABCDPRQF83ABCDPRQtFG8-tt-53(t-5)/43(8-t)/4
1,已知二次函数y=2x2-4x-3,若-1≤X≤5,求y的最大值和最小值。解: y =2x2-4x-3 =2(x2-2x+1)-5=2(x-1)2-5 顶点坐标为(1,-5)而-1≤x≤5 ∴y最小=-5 ∴y最大=27 思考: 若2≤X≤5 y最小=_____,y最大=_____.-3272. 如图,在ΔABC中,AB=8cm
BC=6cm,∠B=90°,点P从点A开始沿AB边向
点B以2厘米/秒的速度移动,点Q从点B开始沿BC
边向点C以1厘米/秒的速度移动,如果P、Q分别
从A、B同时出发。
(1)几秒后,PQ//AC?
(2)几秒后ΔPBQ的面积最大?
最大面积是多少?PQCBA谈谈你的收获小结:用长8m的铝合金条制成如图的矩形窗框,那么当长、宽分别为多少时,才能使窗框的边的透光面积最大?最大的透光面积是多少2.在矩形荒地ABCD中,AB=10,BC=6,现在四边点分别选取了E、F、G、H四点,且AE=AH=CF=CG=X,建一个花园,如何设计可使花园,面积最大?谢谢!
