16.3二次根式的加减 课件(共34张PPT)
文档属性
| 名称 | 16.3二次根式的加减 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 18:29:32 | ||
图片预览










文档简介
(共34张PPT)
16.3 二次根式的加减
第一课时
16.3.1 二次根式的加减
1.掌握二次根式的加减运算法则.
2.会用二次根式的加减运算法则进行简单的运算.
学习目标
重点
难点
回顾:
满足什么条件的根式是最简二次根式
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
新课引入
问题 现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8dm2和18dm2的正方形木板?
7.5dm
5dm
S=8dm2
S=18dm2
新知学习
因为大、小正方形木板的边长分别为
dm和 dm,显然木板够宽.下面考虑木板是否够长.
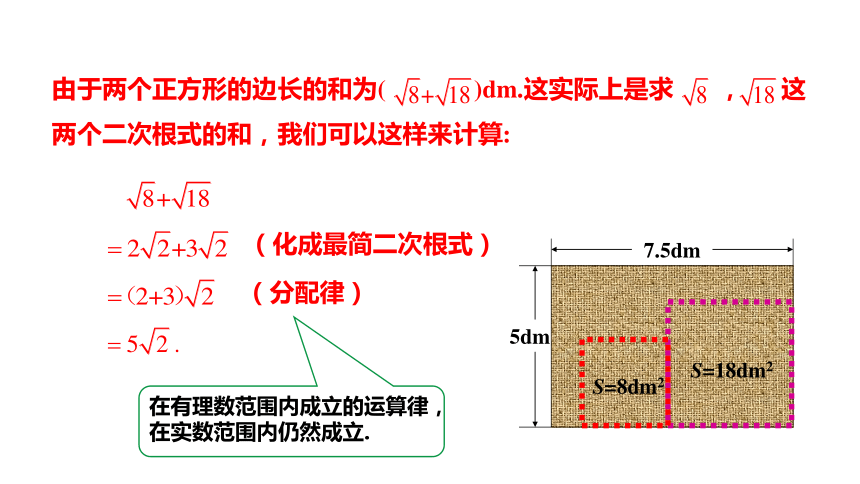
由于两个正方形的边长的和为( )dm.这实际上是求 , 这两个二次根式的和,我们可以这样来计算:
7.5dm
5dm
S=8dm2
S=18dm2
(化成最简二次根式)
(分配律)
在有理数范围内成立的运算律,在实数范围内仍然成立.
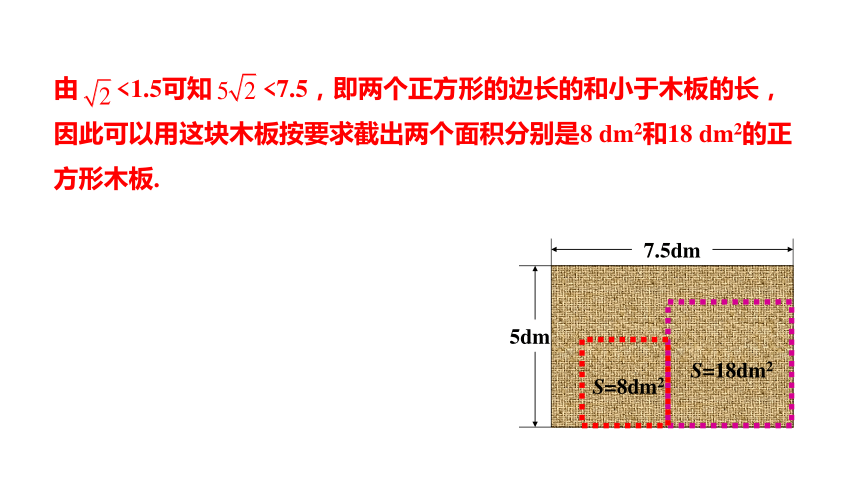
由 <1.5可知 <7.5,即两个正方形的边长的和小于木板的长,
因此可以用这块木板按要求截出两个面积分别是8 dm2和18 dm2的正方形木板.
7.5dm
5dm
S=8dm2
S=18dm2
分析上面计算 的过程,可以看到,把 和 化成最简二次根式 和 后,由于被开方数相同(都是2),可以利用分配律将
和 进行合并.
归纳
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
例1 计算:
解:
例2 计算:
解:
有括号,先去括号
(1)化——将非最简二次根式的二次根式化简为最简二次根式;
二次根式加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化二找三并”
归纳
1.下列计算正确的是 ( )
A. B.
C. D.
C
2.已知一个矩形的长为 ,宽为 ,则其周长为______.
随堂练习
3.计算:
解:
4.如图,两个圆的圆心相同.它们的面积分别为12.56和25.12,求圆环的宽度d(π取3.14,结果保留小数点后两位).
d
由 、 可知
解:设大圆和小圆的半径分别为R,r,面积分别为 , ,
则
答:圆环的宽度d约为0.83.
法则
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
二次根式
的加减
注意
运算原理:运算律仍然适用
运算顺序:与实数的运算顺序一样
课堂小结
16.3.2 二次根式的混合运算
第二课时
1. 掌握二次根式的混合运算法则.
2.熟练地进行二次根式混合运算.
学习目标
重点
难点
回顾:二次根式的加减法法则:
新课引入
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
一 二次根式的混合运算及应用
二次根式的加、减、乘、除混合运算与整式运算一样,体现在:运算律、运算顺序、乘法法则仍然适用.
运算律:交换律、结合律、分配律.
运算顺序:先乘除,再加减,有括号的先算括号内的.
新知学习
例1 计算:
解:
运用了分配律.
解:
运用了多项式
乘法法则.
二 利用乘法公式进行二次根式的运算
你还记得整式乘法运算中的乘法公式有哪些
平方差公式:(a+b)(a-b)=a2-b2;
完全平方公式:(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2.
例2 计算:
解:
在前面我们学习了二次根式的除法法则,学会了怎样去掉分母的二次根式的方法,比如:
思考
如果分母不是单个的二次根式,而是含二次根式的式子,如: 等,该怎样去掉分母中的二次根式呢?
例3 计算:
解:
分母中含有形如 的式子,分子、分母同乘
构成平方差公式,可以使分母不含根号.
三 求代数式的值
例3 已知 试求x2+2xy+y2的值.
解: x2+2xy+y2=(x+y)2
把 代入上式得
原式=
例4 已知 ,求x3y+xy3.
解: x3y+xy3=xy(x2+y2)=xy[(x+y)2-2xy]
∵ ,
∴
∴
整体代入法. 对条件或所求代数式进行适当变换,如化简、合并、拆项、拼凑等,找出条件和所求代数式间的“倍数”关系.
随堂练习
第1题图
本题选自2024《情境题与中考新考法·讲评教案》
2.计算:
解:
3.(1) 已知 ,求 的值;
解:x2-2x-3=(x-3)(x+1)
(2)已知 ,求 的值.
4.在一个边长为 cm的正方形内部,挖去一个边长为
cm的正方形,求剩余部分的面积.
解:由题意得
即剩余部分的面积是
乘法公式
二次根式
的混合运算
化简求值
化简已知条件和所求代数式
分母有理化
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(x+a)(x+b)=x2+(a+b)x+ab
课堂小结
16.3 二次根式的加减
第一课时
16.3.1 二次根式的加减
1.掌握二次根式的加减运算法则.
2.会用二次根式的加减运算法则进行简单的运算.
学习目标
重点
难点
回顾:
满足什么条件的根式是最简二次根式
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
新课引入
问题 现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8dm2和18dm2的正方形木板?
7.5dm
5dm
S=8dm2
S=18dm2
新知学习
因为大、小正方形木板的边长分别为
dm和 dm,显然木板够宽.下面考虑木板是否够长.
由于两个正方形的边长的和为( )dm.这实际上是求 , 这两个二次根式的和,我们可以这样来计算:
7.5dm
5dm
S=8dm2
S=18dm2
(化成最简二次根式)
(分配律)
在有理数范围内成立的运算律,在实数范围内仍然成立.
由 <1.5可知 <7.5,即两个正方形的边长的和小于木板的长,
因此可以用这块木板按要求截出两个面积分别是8 dm2和18 dm2的正方形木板.
7.5dm
5dm
S=8dm2
S=18dm2
分析上面计算 的过程,可以看到,把 和 化成最简二次根式 和 后,由于被开方数相同(都是2),可以利用分配律将
和 进行合并.
归纳
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
例1 计算:
解:
例2 计算:
解:
有括号,先去括号
(1)化——将非最简二次根式的二次根式化简为最简二次根式;
二次根式加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化二找三并”
归纳
1.下列计算正确的是 ( )
A. B.
C. D.
C
2.已知一个矩形的长为 ,宽为 ,则其周长为______.
随堂练习
3.计算:
解:
4.如图,两个圆的圆心相同.它们的面积分别为12.56和25.12,求圆环的宽度d(π取3.14,结果保留小数点后两位).
d
由 、 可知
解:设大圆和小圆的半径分别为R,r,面积分别为 , ,
则
答:圆环的宽度d约为0.83.
法则
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
二次根式
的加减
注意
运算原理:运算律仍然适用
运算顺序:与实数的运算顺序一样
课堂小结
16.3.2 二次根式的混合运算
第二课时
1. 掌握二次根式的混合运算法则.
2.熟练地进行二次根式混合运算.
学习目标
重点
难点
回顾:二次根式的加减法法则:
新课引入
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
一 二次根式的混合运算及应用
二次根式的加、减、乘、除混合运算与整式运算一样,体现在:运算律、运算顺序、乘法法则仍然适用.
运算律:交换律、结合律、分配律.
运算顺序:先乘除,再加减,有括号的先算括号内的.
新知学习
例1 计算:
解:
运用了分配律.
解:
运用了多项式
乘法法则.
二 利用乘法公式进行二次根式的运算
你还记得整式乘法运算中的乘法公式有哪些
平方差公式:(a+b)(a-b)=a2-b2;
完全平方公式:(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2.
例2 计算:
解:
在前面我们学习了二次根式的除法法则,学会了怎样去掉分母的二次根式的方法,比如:
思考
如果分母不是单个的二次根式,而是含二次根式的式子,如: 等,该怎样去掉分母中的二次根式呢?
例3 计算:
解:
分母中含有形如 的式子,分子、分母同乘
构成平方差公式,可以使分母不含根号.
三 求代数式的值
例3 已知 试求x2+2xy+y2的值.
解: x2+2xy+y2=(x+y)2
把 代入上式得
原式=
例4 已知 ,求x3y+xy3.
解: x3y+xy3=xy(x2+y2)=xy[(x+y)2-2xy]
∵ ,
∴
∴
整体代入法. 对条件或所求代数式进行适当变换,如化简、合并、拆项、拼凑等,找出条件和所求代数式间的“倍数”关系.
随堂练习
第1题图
本题选自2024《情境题与中考新考法·讲评教案》
2.计算:
解:
3.(1) 已知 ,求 的值;
解:x2-2x-3=(x-3)(x+1)
(2)已知 ,求 的值.
4.在一个边长为 cm的正方形内部,挖去一个边长为
cm的正方形,求剩余部分的面积.
解:由题意得
即剩余部分的面积是
乘法公式
二次根式
的混合运算
化简求值
化简已知条件和所求代数式
分母有理化
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(x+a)(x+b)=x2+(a+b)x+ab
课堂小结
