单项式乘多项式
图片预览








文档简介
课件20张PPT。15.1.4单项式乘以多项式
2008.12.13学习目标1、了解单项式乘以多项式的意义;
2、能概括、理解单项式乘以多项式的法则;
3、会利用法则进行单项式乘以多项式的运算.自学指导自学时间4分钟自学第145页和146页的内容,能回答下列问题:
1、什么是单项式与多项式的乘法?
2、单项式与多项式相乘法,法则是什么?
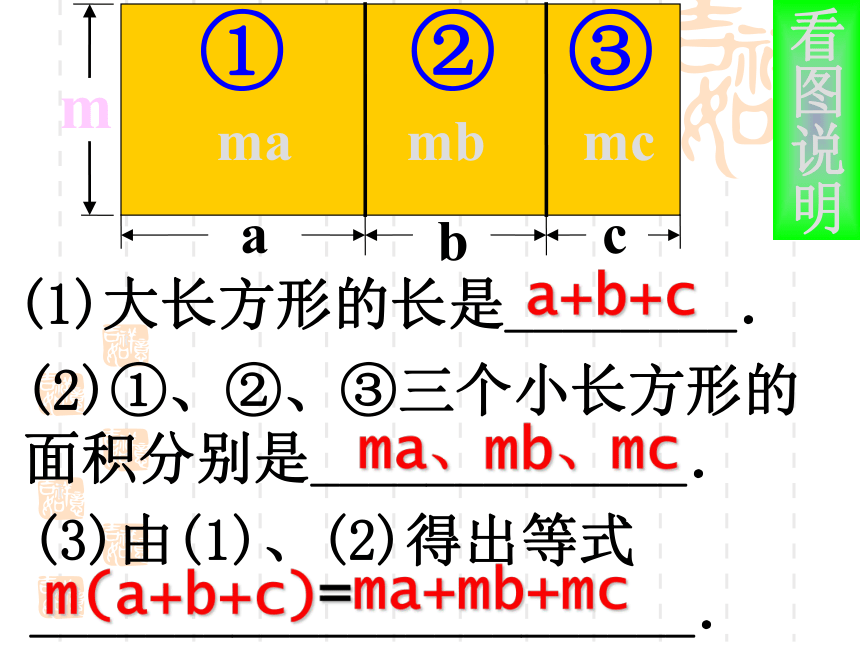
3、看例5的计算,看看是如何运用法则进行计算的?m(a+b+c)=ma+mb+mc(m、a、b、c都是单项式)(1)大长方形的长是________.(2)①、②、③三个小长方形的 面积分别是_____________.(3)由(1)、(2)得出等式
_______________________.①②③a+b+cma、mb、mcm(a+b+c)看图说明=ma+mb+mc(-2a)?(2a2-3a+1)=(-2a)?2a2=-4a3+6a2-2a(乘法分配律)(单项式与单项式相乘法则)(-2a)?(-3a)(-2a)?1++练习1怎样叙述单项式与多项式相乘的法则? m(a+b+c)=ma+mb+mc
(m、a、b、c都是单项式)单项式与多项式相乘法则 单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加 m(a+b+c)=ma+mb+mc
(m、a、b、c都是单项式)练习2计算(1)(-4x)·(2x2+3x-1); 解: (-4x)·(2x2+3x-1)==-8x3-12x2+4x注意:(-1)这项不要漏乘,也不要当成是1; (-4x)·(2x2)(-4x)·3x(-4x)·(-1)+++单项式与多项式相乘时,分三个阶段:①按乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;②单项式的乘法运算;③再把所得的积相加.几点注意:1.单项式乘多项式的结果仍是多项式,积的项数与原多项式的项数相同。2.单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:同号相乘得正,异号相乘得负. 3.不要出现漏乘现象,运算要有顺序。(1)(3x2y-xy2)·(-3xy) 练习3(计算)一.判断××1.m(a+b+c+d)=ma+b+c+d( )( )3.(-2x)?(ax+b-3)=-2ax2-2bx-6x( )×当堂检测1.单项式与多项式相乘,就是用单项式去乘
多项式的________,再把所得的积________二.填空2.4(a-b+1)=___________________每一项相加4a-4b+43.3x(2x-y2)=___________________6x2-3xy24.-3x(2x-5y+6z)=___________________-6x2+15xy-18xz5.(-2a2)2(-a-2b+c)=___________________-4a5-8a4b+4a4c三.选择下列计算错误的是( )
(A)5x(2x2-y)=10x3-5xy
(B)-3xa+b ?4xa-b=-12x2a
(C)2a2b?4ab2=8a3b3
(D)(-xn-1y2)?(-xym)2=xnym+2 D=(-xn-1y2)?(x2y2m)=-xn+1y2m+2 (-2ab)3(5a2b–2b3)解:原式=(-8a3b3)(5a2b–2b3) =(-8a3b3)·(5a2b)+(-8a3b3)·(-2b3) =-40a5b4+16a3b6说明:先进行乘方运算,再进行单项式与多项式的乘法运算。4、计算:5、 计算:-2a2·(ab+b2)-5a(a2b-ab2) 解:原式=-2a3b-2a2b2-5a3b+5a2b2=-2a3b-2a2b2-5a3b+5a2b2注意:
1.将-2a2与-5a的“-”看成性质符号
2.单项式与多项式相乘的结果中,应将同类项合并。 =-7a3b+3a2b2 yn(yn +9y-12)–3(3yn+1-4yn),
其中y=-3,n=2.解:yn(yn + 9y-12)–3(3yn+1-4yn)=y2n+9yn+1-12yn–9yn+1+12yn=y2n当y=-3,n=2时,原式=(-3)2×2=(-3)4=816、化简求值:小结这节课学习的主要内容?(口答)
2008.12.13学习目标1、了解单项式乘以多项式的意义;
2、能概括、理解单项式乘以多项式的法则;
3、会利用法则进行单项式乘以多项式的运算.自学指导自学时间4分钟自学第145页和146页的内容,能回答下列问题:
1、什么是单项式与多项式的乘法?
2、单项式与多项式相乘法,法则是什么?
3、看例5的计算,看看是如何运用法则进行计算的?m(a+b+c)=ma+mb+mc(m、a、b、c都是单项式)(1)大长方形的长是________.(2)①、②、③三个小长方形的 面积分别是_____________.(3)由(1)、(2)得出等式
_______________________.①②③a+b+cma、mb、mcm(a+b+c)看图说明=ma+mb+mc(-2a)?(2a2-3a+1)=(-2a)?2a2=-4a3+6a2-2a(乘法分配律)(单项式与单项式相乘法则)(-2a)?(-3a)(-2a)?1++练习1怎样叙述单项式与多项式相乘的法则? m(a+b+c)=ma+mb+mc
(m、a、b、c都是单项式)单项式与多项式相乘法则 单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加 m(a+b+c)=ma+mb+mc
(m、a、b、c都是单项式)练习2计算(1)(-4x)·(2x2+3x-1); 解: (-4x)·(2x2+3x-1)==-8x3-12x2+4x注意:(-1)这项不要漏乘,也不要当成是1; (-4x)·(2x2)(-4x)·3x(-4x)·(-1)+++单项式与多项式相乘时,分三个阶段:①按乘法分配律把乘积写成单项式与单项式乘积的代数和的形式;②单项式的乘法运算;③再把所得的积相加.几点注意:1.单项式乘多项式的结果仍是多项式,积的项数与原多项式的项数相同。2.单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:同号相乘得正,异号相乘得负. 3.不要出现漏乘现象,运算要有顺序。(1)(3x2y-xy2)·(-3xy) 练习3(计算)一.判断××1.m(a+b+c+d)=ma+b+c+d( )( )3.(-2x)?(ax+b-3)=-2ax2-2bx-6x( )×当堂检测1.单项式与多项式相乘,就是用单项式去乘
多项式的________,再把所得的积________二.填空2.4(a-b+1)=___________________每一项相加4a-4b+43.3x(2x-y2)=___________________6x2-3xy24.-3x(2x-5y+6z)=___________________-6x2+15xy-18xz5.(-2a2)2(-a-2b+c)=___________________-4a5-8a4b+4a4c三.选择下列计算错误的是( )
(A)5x(2x2-y)=10x3-5xy
(B)-3xa+b ?4xa-b=-12x2a
(C)2a2b?4ab2=8a3b3
(D)(-xn-1y2)?(-xym)2=xnym+2 D=(-xn-1y2)?(x2y2m)=-xn+1y2m+2 (-2ab)3(5a2b–2b3)解:原式=(-8a3b3)(5a2b–2b3) =(-8a3b3)·(5a2b)+(-8a3b3)·(-2b3) =-40a5b4+16a3b6说明:先进行乘方运算,再进行单项式与多项式的乘法运算。4、计算:5、 计算:-2a2·(ab+b2)-5a(a2b-ab2) 解:原式=-2a3b-2a2b2-5a3b+5a2b2=-2a3b-2a2b2-5a3b+5a2b2注意:
1.将-2a2与-5a的“-”看成性质符号
2.单项式与多项式相乘的结果中,应将同类项合并。 =-7a3b+3a2b2 yn(yn +9y-12)–3(3yn+1-4yn),
其中y=-3,n=2.解:yn(yn + 9y-12)–3(3yn+1-4yn)=y2n+9yn+1-12yn–9yn+1+12yn=y2n当y=-3,n=2时,原式=(-3)2×2=(-3)4=816、化简求值:小结这节课学习的主要内容?(口答)
