浙江省杭州市富阳区2023-2024学年高二上学期期末考试数学试题(含答案)
文档属性
| 名称 | 浙江省杭州市富阳区2023-2024学年高二上学期期末考试数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 630.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-23 00:00:00 | ||
图片预览


文档简介
富阳区2023-2024学年高二上学期期末考试数学试题
学号____________ 姓名____________
一、选择题:本题共8小题,每小题5分,共40分.
1.设集合,,则 ( )
A. B. C. D.
2.已知,则 ( )
A. B. C. D.
3.已知直线和,则“”是“”的 ( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件
4.已知,,且,,则 ( )
A. B. C. D.
5.已知双曲线,若存在圆心在双曲线的一条渐近线上的圆,它与另一条渐近线、轴都相切,则该双曲线的离心率为 ( )
A.3 B. C. D.2
6.现有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球.事件“第一次取出的球的数字是3”,事件“第二次取出的球的数字是2”,事件“两次取出的球的数字之和是7”,事件“两次取出的球的数字之和是6”,则 ( )
A.与相互独立 B.与相互独立 C.与相互独立 D.与相互独立
7.已知函数和都是定义在上的偶函数,当时,,则( )
A. B. C. D.
8.已知实数,满足,则的取值范围是 ( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的或不选的得0分.
9.已知把函数的图象上所有点向右平移个单位长度,可得到函数图象,( )
A. B.
C. D.
10.已知为坐标原点,点,,,,则 ( )
A. B. C. D.
11.在平面直角坐标系中,三点,,,动点满足,则 ( )
A.点的轨迹方程为 B.面积最大时
C.最大时, D.到直线距离最小值为
12.正三棱柱中,,点满足,其中,,则( )
A.当时,的周长为定值 B.当时,三棱锥的体积为定值
C.当时,有且仅有一个点,使 D.当时,有且仅有一个点,使平面
三、填空题:本大题共4小题,每题5分,双空题第一空2分,第二空3分,共20分.
13.在中,已知,,,则 .
14.表面积为16π的球的内接轴截面为正方形的圆柱的体积为__________.
15.已知是椭圆的左右顶点,点分别在矩形的边上,,且与的交点在椭圆上(第一象限内),则_______.
16.如图,在三棱锥中,若底面是正三角形,侧棱长,、分别为棱、的中点,并且,则直线与面所成角的正切值为 ;三棱锥的外接球的体积为 .
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本题10分)近年来,在新高考改革中,打破文理分科的“3+3模式初露端倪,其中,语、数、英三门为必考科目,剩下三门为选考科目(物理、化学、生物、政治、历史、地理).选考科目采用赋分”,即原始分不直接使用,而是按照学生在本科目考试的排名来划分等级,并以此打分得到最后的得分,假定某省规定:选考科目按考生原始分数从高到低排列,按照占总体15%,35%,35%,13%和2%划定A、B、C、D、E五个等级,并分别赋分为90分、80分、70分、60分和50分.该省某高中高二(11)班(共40人)进行了一次模拟考试选考科目全考,单科全班排名,(已知这次模拟考试中历史成绩满分100分)的频率分布直方图和地理成绩的成绩单如下所示,李雷同学这次考试中历史82分,地理70多分.
(Ⅰ)采用赋分制后,求李雷同学历史成绩的最终得分;
(Ⅱ)采用赋分制后,若李雷同学地理成绩最终得分为80分,那么他地理成绩原始分的所有可能值是多少?
(Ⅲ)若韩梅同学必选历史,从地理、政治、物理、化学、生物五科中等可能地任选两科,则她选考科目中包含地理的概率是多少?
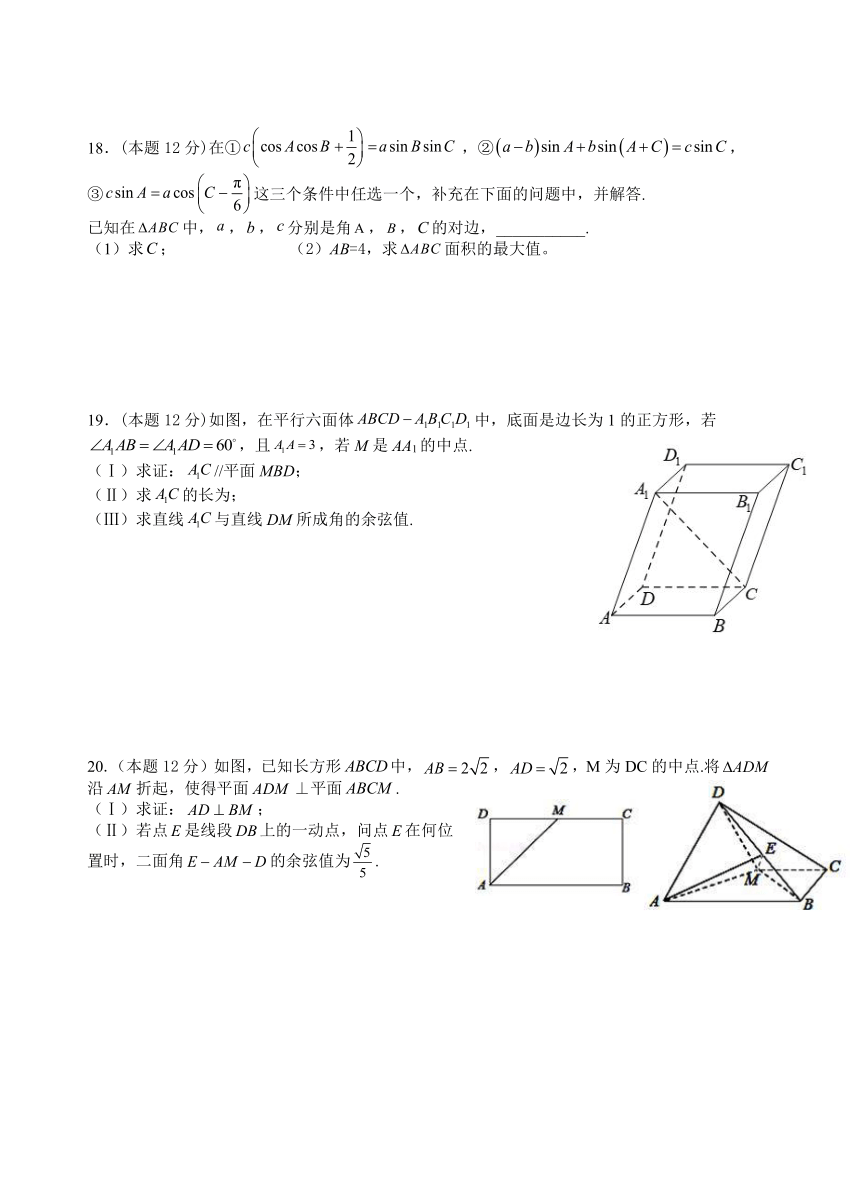
18.(本题12分)在①,②,③这三个条件中任选一个,补充在下面的问题中,并解答.
已知在中,,,分别是角,,的对边,___________.
(1)求; (2)AB=4,求面积的最大值。
19.(本题12分)如图,在平行六面体中,底面是边长为1的正方形,若,且,若M是AA1的中点.
(Ⅰ)求证://平面MBD;
(Ⅱ)求的长为;
(Ⅲ)求直线与直线DM所成角的余弦值.
20.(本题12分)如图,已知长方形中,,,M为DC的中点.将沿折起,使得平面⊥平面.
(Ⅰ)求证:;
(Ⅱ)若点是线段上的一动点,问点在何位置时,二面角的余弦值为.
21. (本题12分)如图,直线与圆相切于点,与抛物线相交于不同的两点,与轴相交于点.
(Ⅰ)若是抛物线的焦点,求直线的方程;
(Ⅱ)若,求的值.
22. (本题12分)设,已知函数,的零点分别是,,且.
(Ⅰ)若,求a的取值范围;
(Ⅱ)若,证明:;
(Ⅲ)若,证明:.
参考答案
1-8 BCBCD ADA 9. AC 10 .AC 11. ABD 12. BD
13. 或, 14. 15. 16.
17.解(1)80分以上的占,属于级,赋分制得分为90分.
(2)采用赋分制后,李雷同学地理成绩的最终得分为80分,故成绩在到之间,
,,故成绩在名和名之间,即到之间,
地理70多分,故可能的原始分数为76,77,78.
(3)记地理、政治、物理、化学、生物分别为,
共有10种情况,
满足条件的有4种,故.
18(1)方案一:选条件①.∵,∴,
∵,∴,即,
∵,∴,即,∵,∴.
方案二:选条件②.∵,∴.
∴,即,∴,∵,∴.
方案三:选条件③.由及正弦定理得,
∵,∴,∴,即,得,
故,又,∴.
(2)
19.解(1)连交于,连,则为的中点,又是的中点,所以,
又平面,平面,所以平面.
(2)因为,
所以
.
(3)设直线与直线DM所成角为,则,
因为,所以
,
因为,,
所以
.
所以直线与直线DM所成角的余弦值为.
20. (1)证明:∵长方形ABCD中,AB=,AD=,M为DC的中点,
∴AM=BM=2,∴BM⊥AM.
∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM 平面ABCM
∴BM⊥平面ADM
∵AD 平面ADM ∴AD⊥BM.
(2)建立如图所示的直角坐标系
设,则平面AMD的一个法向量,
,
设平面AME的一个法向量则
取y=1,得
所以,因为,求得,
所以E为BD的中点.
21. 解:(1)因为是抛物线的焦点,所以,即,
设直线的方程为,由直线与圆相切,得,即,
所以,直线的方程为.
(2)设直线的方程为,,,,
由,得,,,
∴.
由直线与圆相切,得,即.
由,,得.
所以,又,解得.
由直线与互相垂直,得,
.
22. 解:(Ⅰ)因为在上单调递增,且,所以,且.
所以,,且,所以,.所以实数a的取值范围.
(Ⅱ)当时,在上单调递增,且,所以,.
因为在上单调递增,,所以,.
所以,对任意的恒成立,
所以,,所以,.
(Ⅲ)当时,在上单调递增,且,
所以,,因为在上单调递增.所以,,因为,
,所以,
,故,.
试卷第6页,共7页
学号____________ 姓名____________
一、选择题:本题共8小题,每小题5分,共40分.
1.设集合,,则 ( )
A. B. C. D.
2.已知,则 ( )
A. B. C. D.
3.已知直线和,则“”是“”的 ( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件
4.已知,,且,,则 ( )
A. B. C. D.
5.已知双曲线,若存在圆心在双曲线的一条渐近线上的圆,它与另一条渐近线、轴都相切,则该双曲线的离心率为 ( )
A.3 B. C. D.2
6.现有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球.事件“第一次取出的球的数字是3”,事件“第二次取出的球的数字是2”,事件“两次取出的球的数字之和是7”,事件“两次取出的球的数字之和是6”,则 ( )
A.与相互独立 B.与相互独立 C.与相互独立 D.与相互独立
7.已知函数和都是定义在上的偶函数,当时,,则( )
A. B. C. D.
8.已知实数,满足,则的取值范围是 ( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的或不选的得0分.
9.已知把函数的图象上所有点向右平移个单位长度,可得到函数图象,( )
A. B.
C. D.
10.已知为坐标原点,点,,,,则 ( )
A. B. C. D.
11.在平面直角坐标系中,三点,,,动点满足,则 ( )
A.点的轨迹方程为 B.面积最大时
C.最大时, D.到直线距离最小值为
12.正三棱柱中,,点满足,其中,,则( )
A.当时,的周长为定值 B.当时,三棱锥的体积为定值
C.当时,有且仅有一个点,使 D.当时,有且仅有一个点,使平面
三、填空题:本大题共4小题,每题5分,双空题第一空2分,第二空3分,共20分.
13.在中,已知,,,则 .
14.表面积为16π的球的内接轴截面为正方形的圆柱的体积为__________.
15.已知是椭圆的左右顶点,点分别在矩形的边上,,且与的交点在椭圆上(第一象限内),则_______.
16.如图,在三棱锥中,若底面是正三角形,侧棱长,、分别为棱、的中点,并且,则直线与面所成角的正切值为 ;三棱锥的外接球的体积为 .
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本题10分)近年来,在新高考改革中,打破文理分科的“3+3模式初露端倪,其中,语、数、英三门为必考科目,剩下三门为选考科目(物理、化学、生物、政治、历史、地理).选考科目采用赋分”,即原始分不直接使用,而是按照学生在本科目考试的排名来划分等级,并以此打分得到最后的得分,假定某省规定:选考科目按考生原始分数从高到低排列,按照占总体15%,35%,35%,13%和2%划定A、B、C、D、E五个等级,并分别赋分为90分、80分、70分、60分和50分.该省某高中高二(11)班(共40人)进行了一次模拟考试选考科目全考,单科全班排名,(已知这次模拟考试中历史成绩满分100分)的频率分布直方图和地理成绩的成绩单如下所示,李雷同学这次考试中历史82分,地理70多分.
(Ⅰ)采用赋分制后,求李雷同学历史成绩的最终得分;
(Ⅱ)采用赋分制后,若李雷同学地理成绩最终得分为80分,那么他地理成绩原始分的所有可能值是多少?
(Ⅲ)若韩梅同学必选历史,从地理、政治、物理、化学、生物五科中等可能地任选两科,则她选考科目中包含地理的概率是多少?
18.(本题12分)在①,②,③这三个条件中任选一个,补充在下面的问题中,并解答.
已知在中,,,分别是角,,的对边,___________.
(1)求; (2)AB=4,求面积的最大值。
19.(本题12分)如图,在平行六面体中,底面是边长为1的正方形,若,且,若M是AA1的中点.
(Ⅰ)求证://平面MBD;
(Ⅱ)求的长为;
(Ⅲ)求直线与直线DM所成角的余弦值.
20.(本题12分)如图,已知长方形中,,,M为DC的中点.将沿折起,使得平面⊥平面.
(Ⅰ)求证:;
(Ⅱ)若点是线段上的一动点,问点在何位置时,二面角的余弦值为.
21. (本题12分)如图,直线与圆相切于点,与抛物线相交于不同的两点,与轴相交于点.
(Ⅰ)若是抛物线的焦点,求直线的方程;
(Ⅱ)若,求的值.
22. (本题12分)设,已知函数,的零点分别是,,且.
(Ⅰ)若,求a的取值范围;
(Ⅱ)若,证明:;
(Ⅲ)若,证明:.
参考答案
1-8 BCBCD ADA 9. AC 10 .AC 11. ABD 12. BD
13. 或, 14. 15. 16.
17.解(1)80分以上的占,属于级,赋分制得分为90分.
(2)采用赋分制后,李雷同学地理成绩的最终得分为80分,故成绩在到之间,
,,故成绩在名和名之间,即到之间,
地理70多分,故可能的原始分数为76,77,78.
(3)记地理、政治、物理、化学、生物分别为,
共有10种情况,
满足条件的有4种,故.
18(1)方案一:选条件①.∵,∴,
∵,∴,即,
∵,∴,即,∵,∴.
方案二:选条件②.∵,∴.
∴,即,∴,∵,∴.
方案三:选条件③.由及正弦定理得,
∵,∴,∴,即,得,
故,又,∴.
(2)
19.解(1)连交于,连,则为的中点,又是的中点,所以,
又平面,平面,所以平面.
(2)因为,
所以
.
(3)设直线与直线DM所成角为,则,
因为,所以
,
因为,,
所以
.
所以直线与直线DM所成角的余弦值为.
20. (1)证明:∵长方形ABCD中,AB=,AD=,M为DC的中点,
∴AM=BM=2,∴BM⊥AM.
∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM 平面ABCM
∴BM⊥平面ADM
∵AD 平面ADM ∴AD⊥BM.
(2)建立如图所示的直角坐标系
设,则平面AMD的一个法向量,
,
设平面AME的一个法向量则
取y=1,得
所以,因为,求得,
所以E为BD的中点.
21. 解:(1)因为是抛物线的焦点,所以,即,
设直线的方程为,由直线与圆相切,得,即,
所以,直线的方程为.
(2)设直线的方程为,,,,
由,得,,,
∴.
由直线与圆相切,得,即.
由,,得.
所以,又,解得.
由直线与互相垂直,得,
.
22. 解:(Ⅰ)因为在上单调递增,且,所以,且.
所以,,且,所以,.所以实数a的取值范围.
(Ⅱ)当时,在上单调递增,且,所以,.
因为在上单调递增,,所以,.
所以,对任意的恒成立,
所以,,所以,.
(Ⅲ)当时,在上单调递增,且,
所以,,因为在上单调递增.所以,,因为,
,所以,
,故,.
试卷第6页,共7页
同课章节目录
