人教版数学八年级下册同步练习17.1.1 勾股定理的发现和证明(含答案)
文档属性
| 名称 | 人教版数学八年级下册同步练习17.1.1 勾股定理的发现和证明(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 267.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-25 09:16:26 | ||
图片预览

文档简介
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理的发现和证明
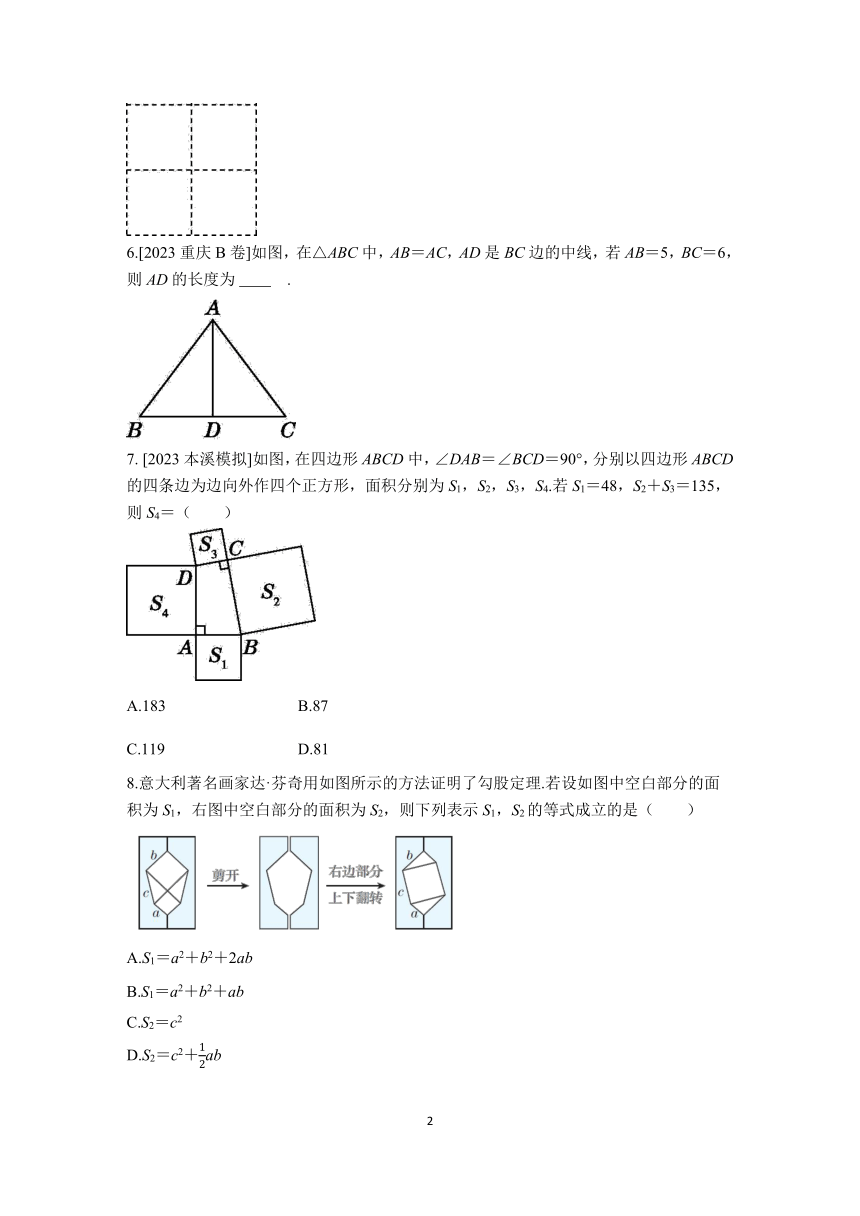
1.以直角三角形的三边为边向外作正方形,图中字母所代表的正方形的面积为175的选项为( )
2.[2023盘锦盘山期末]如图,点E在正方形ABCD的边AB上,若EB=2,EC=5,则正方形ABCD的面积为( )
A.15 B.17
C.10 D.18
3.如图,在△ABC中,∠C=90°,若a=9,b=12,则c= ;若c=2,则a2+b2= .
4.如图,直线l经过正方形ABCD的顶点B,点A,C到直线l的距离分别是1,3,则正方形ABCD的面积是 .
5.如图是由4个边长为1的正方形构成的“田字格”.只用没有刻度的直尺在这个“田字格”中最多可以作出以格点为端点、长度为的线段 条.
6.[2023重庆B卷]如图,在△ABC中,AB=AC,AD是BC边的中线,若AB=5,BC=6,则AD的长度为 .
7. [2023本溪模拟]如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形ABCD的四条边为边向外作四个正方形,面积分别为S1,S2,S3,S4.若S1=48,S2+S3=135,则S4=( )
A.183 B.87
C.119 D.81
8.意大利著名画家达·芬奇用如图所示的方法证明了勾股定理.若设如图中空白部分的面积为S1,右图中空白部分的面积为S2,则下列表示S1,S2的等式成立的是( )
A.S1=a2+b2+2ab
B.S1=a2+b2+ab
C.S2=c2
D.S2=c2+ab
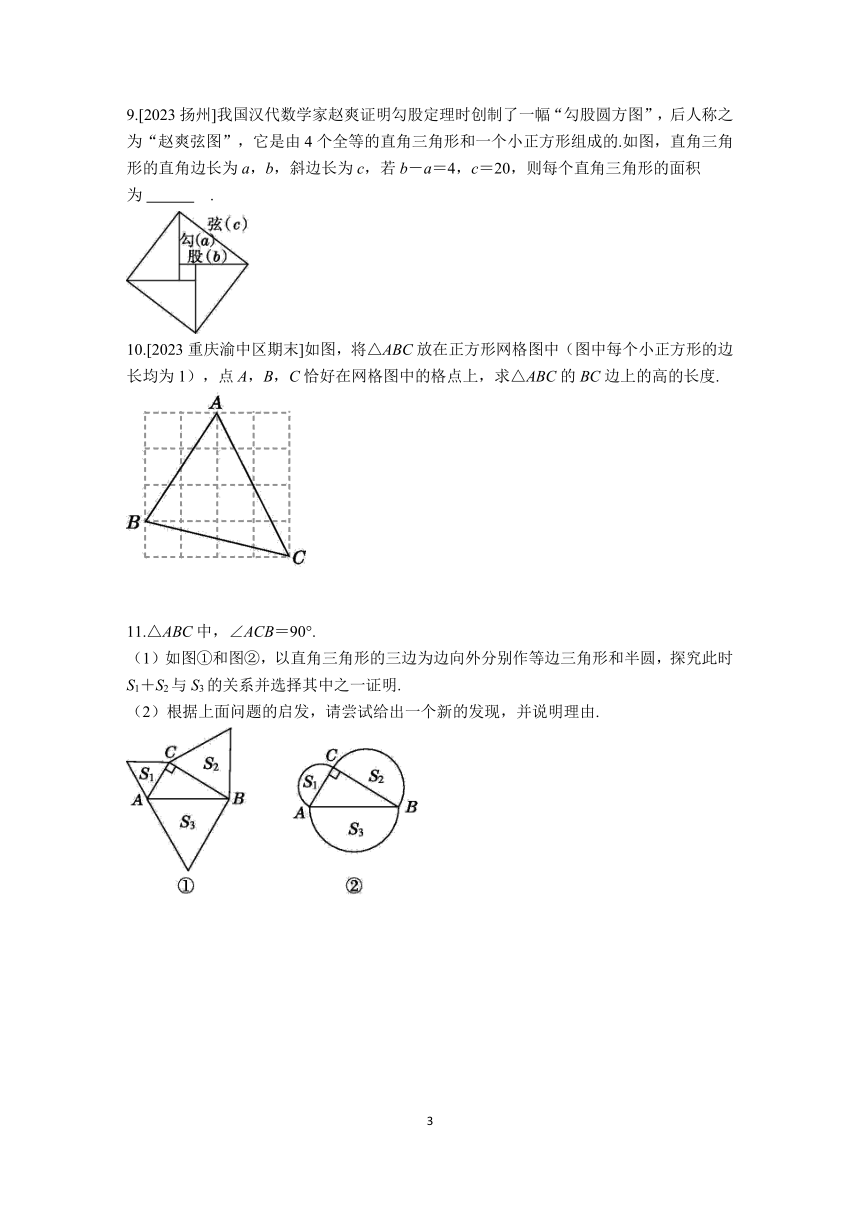
9.[2023扬州]我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成的.如图,直角三角形的直角边长为a,b,斜边长为c,若b-a=4,c=20,则每个直角三角形的面积为 .
10.[2023重庆渝中区期末]如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,求△ABC的BC边上的高的长度.
11.△ABC中,∠ACB=90°.
(1)如图①和图②,以直角三角形的三边为边向外分别作等边三角形和半圆,探究此时S1+S2与S3的关系并选择其中之一证明.
(2)根据上面问题的启发,请尝试给出一个新的发现,并说明理由.
12.[2023南京模拟]如图,在△ACB中,∠ACB=90°,AC=BC,且AB=2,分别以AB,AC,BC为直径画半圆,其中所得两个月形图案AFCD和BGCE(图中阴影部分)的面积之和等于( )
A.8 B.4
C.2 D.4
13.【学科素养 创新意识】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同.其中的“面积法”给了小聪灵感.他发现:当两个全等的直角三角形如图①或图②所示摆放时,都可以用“面积法”来证明.下面是小聪利用图①证明勾股定理的过程:
将两个全等的直角三角形按图①所示的方式摆放,其中∠DAB=90°,
求证:a2+b2=c2.
证明:连接DB, DC,过点D作BC边上的高DF,易得DF= EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=b2+ab,
S四边形ADCB=S△ADB+S△DCB=c2+a(b-a),
∴b2+ab=c2+a(b-a),
∴a2+b2=c2.
请参照上述证法,利用图②完成勾股定理的证明.
6
参考答案
1.A 2.B 3.15;4 4.10 5.8 6.4
7.B 点拨:由题意可知:S1=AB2,S2=BC2,S3=CD2,S4=AD2,连接BD,∵∠DAB=∠BCD=90°,∴BD2=AD2+AB2=CD2+BC2,即S1+S4=S3+S2,因此S4=135-48=87,故选B.
8.B 9.96
10.解:根据图形可得:△ABC的面积为:16-×1×4-×3×2-×2×4=7,
BC==,
设△ABC中BC边上的高是x,则BC·x=7,
∴x=.
11.解:(1)S1+S2=S3.
证明如下:设BC=a,AC=b,AB=c.
在图①中,易得S1=b2,S2=a2,S3=c2,
则S1+S2=(a2+b2),
因为a2+b2=c2,所以S1+S2=S3.
在图②中,S1=πb2,S2=πa2,S3=πc2.
则S1+S2=π(a2+b2),
因为a2+b2=c2,
所以S1+S2=S3.
(2)以直角三角形的三边为斜边向外分别作等腰直角三角形,同样满足S1+S2=S3.
易知S1=AC2,S2=BC2,S3=AB2.
则S1+S2=(AC2+BC2),
因为AC2+BC2=AB2,
所以S1+S2=S3.(答案不唯一)
12.C 点拨:在△ACB中,∠ACB=90°,AC=BC,AB=2,
∴AC2+BC2=AB2=8=2AC2,∴AC=CB=2,
∴S△ACB=AC·BC=2,
∴S阴影=π+S△ACB-π=π+2-π=2,故选C.
13.证明:如图,连接BD,过点B作DE边上的高BF,易得BF=b-a,
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab,S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a,
∴ab+b2+ab=ab+c2+a(b-a),
∴a2+b2=c2.
17.1 勾股定理
第1课时 勾股定理的发现和证明
1.以直角三角形的三边为边向外作正方形,图中字母所代表的正方形的面积为175的选项为( )
2.[2023盘锦盘山期末]如图,点E在正方形ABCD的边AB上,若EB=2,EC=5,则正方形ABCD的面积为( )
A.15 B.17
C.10 D.18
3.如图,在△ABC中,∠C=90°,若a=9,b=12,则c= ;若c=2,则a2+b2= .
4.如图,直线l经过正方形ABCD的顶点B,点A,C到直线l的距离分别是1,3,则正方形ABCD的面积是 .
5.如图是由4个边长为1的正方形构成的“田字格”.只用没有刻度的直尺在这个“田字格”中最多可以作出以格点为端点、长度为的线段 条.
6.[2023重庆B卷]如图,在△ABC中,AB=AC,AD是BC边的中线,若AB=5,BC=6,则AD的长度为 .
7. [2023本溪模拟]如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形ABCD的四条边为边向外作四个正方形,面积分别为S1,S2,S3,S4.若S1=48,S2+S3=135,则S4=( )
A.183 B.87
C.119 D.81
8.意大利著名画家达·芬奇用如图所示的方法证明了勾股定理.若设如图中空白部分的面积为S1,右图中空白部分的面积为S2,则下列表示S1,S2的等式成立的是( )
A.S1=a2+b2+2ab
B.S1=a2+b2+ab
C.S2=c2
D.S2=c2+ab
9.[2023扬州]我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成的.如图,直角三角形的直角边长为a,b,斜边长为c,若b-a=4,c=20,则每个直角三角形的面积为 .
10.[2023重庆渝中区期末]如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,求△ABC的BC边上的高的长度.
11.△ABC中,∠ACB=90°.
(1)如图①和图②,以直角三角形的三边为边向外分别作等边三角形和半圆,探究此时S1+S2与S3的关系并选择其中之一证明.
(2)根据上面问题的启发,请尝试给出一个新的发现,并说明理由.
12.[2023南京模拟]如图,在△ACB中,∠ACB=90°,AC=BC,且AB=2,分别以AB,AC,BC为直径画半圆,其中所得两个月形图案AFCD和BGCE(图中阴影部分)的面积之和等于( )
A.8 B.4
C.2 D.4
13.【学科素养 创新意识】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同.其中的“面积法”给了小聪灵感.他发现:当两个全等的直角三角形如图①或图②所示摆放时,都可以用“面积法”来证明.下面是小聪利用图①证明勾股定理的过程:
将两个全等的直角三角形按图①所示的方式摆放,其中∠DAB=90°,
求证:a2+b2=c2.
证明:连接DB, DC,过点D作BC边上的高DF,易得DF= EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=b2+ab,
S四边形ADCB=S△ADB+S△DCB=c2+a(b-a),
∴b2+ab=c2+a(b-a),
∴a2+b2=c2.
请参照上述证法,利用图②完成勾股定理的证明.
6
参考答案
1.A 2.B 3.15;4 4.10 5.8 6.4
7.B 点拨:由题意可知:S1=AB2,S2=BC2,S3=CD2,S4=AD2,连接BD,∵∠DAB=∠BCD=90°,∴BD2=AD2+AB2=CD2+BC2,即S1+S4=S3+S2,因此S4=135-48=87,故选B.
8.B 9.96
10.解:根据图形可得:△ABC的面积为:16-×1×4-×3×2-×2×4=7,
BC==,
设△ABC中BC边上的高是x,则BC·x=7,
∴x=.
11.解:(1)S1+S2=S3.
证明如下:设BC=a,AC=b,AB=c.
在图①中,易得S1=b2,S2=a2,S3=c2,
则S1+S2=(a2+b2),
因为a2+b2=c2,所以S1+S2=S3.
在图②中,S1=πb2,S2=πa2,S3=πc2.
则S1+S2=π(a2+b2),
因为a2+b2=c2,
所以S1+S2=S3.
(2)以直角三角形的三边为斜边向外分别作等腰直角三角形,同样满足S1+S2=S3.
易知S1=AC2,S2=BC2,S3=AB2.
则S1+S2=(AC2+BC2),
因为AC2+BC2=AB2,
所以S1+S2=S3.(答案不唯一)
12.C 点拨:在△ACB中,∠ACB=90°,AC=BC,AB=2,
∴AC2+BC2=AB2=8=2AC2,∴AC=CB=2,
∴S△ACB=AC·BC=2,
∴S阴影=π+S△ACB-π=π+2-π=2,故选C.
13.证明:如图,连接BD,过点B作DE边上的高BF,易得BF=b-a,
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab,S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a,
∴ab+b2+ab=ab+c2+a(b-a),
∴a2+b2=c2.
