人教版数学八年级下册同步练习17.2 勾股定理的逆定理(含答案)
文档属性
| 名称 | 人教版数学八年级下册同步练习17.2 勾股定理的逆定理(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 91.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-25 09:18:07 | ||
图片预览

文档简介
第十七章 勾股定理
17.2 勾股定理的逆定理
1.(桂林中考)下列各组线段能构成直角三角形的一组是( )
A.30,40,50 B.7,12,13 C.5,9,12 D.3,4,6
2.在△ABC中,AB=12cm,BC=16cm,AC=20cm,则△ABC的面积是( )
A.96cm2 B.120cm2 C.160cm2 D.200cm2
3.已知a、b、c是△ABC的三边长,且满足关系式+|a-b|=0,则△ABC的形状为 .
4.下列各组数据中,是勾股数的为( )
A.1,, B.8,15,17 C.32,42,52 D.,,1
5.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出具有以上规律的第⑥组勾股数 .
6.写出下列各命题的逆命题,并判断逆命题的真假性:
(1)两直线平行,同位角相等;
(2)全等三角形的对应角相等;
(3)线段垂直平分线上的点到线段的两个端点的距离相等;
(4)如果a是偶数,则2a是偶数.
7.下列各组数中,不是勾股数的一组是( )
A.7,24,25 B.4,5,6 C.5,12,13 D.8,15,17
8.a、b、c是△ABC的∠A、∠B、∠C的对边,且a∶b∶c=1∶∶,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
9.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )
10.在△ABC中,a=5,b=6,当c= 时,∠C是直角;当c= 时,∠B是直角.
11.“等腰三角形两腰上的高相等”的逆命题是
,这个命题是 (填“正确”或“错误”)的.
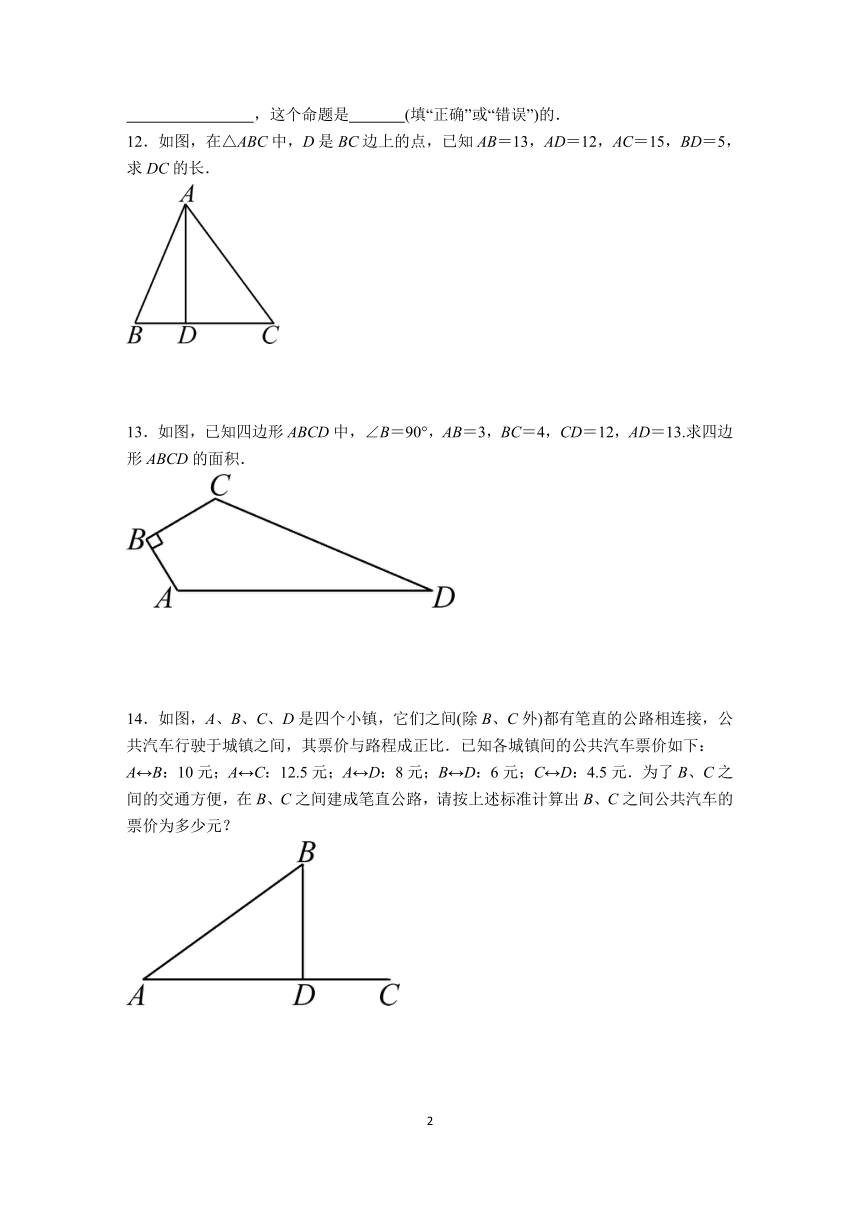
12.如图,在△ABC中,D是BC边上的点,已知AB=13,AD=12,AC=15,BD=5,求DC的长.
13.如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13.求四边形ABCD的面积.
14.如图,A、B、C、D是四个小镇,它们之间(除B、C外)都有笔直的公路相连接,公共汽车行驶于城镇之间,其票价与路程成正比.已知各城镇间的公共汽车票价如下:A B:10元;A C:12.5元;A D:8元;B D:6元;C D:4.5元.为了B、C之间的交通方便,在B、C之间建成笔直公路,请按上述标准计算出B、C之间公共汽车的票价为多少元?
15.(宜昌中考)阅读:能够成为直角三角形三边长的三个正整数a、b、c称为勾股数,世界上第一次给出勾股数通解公式的是我国古代的数学著作《九章算术》,其勾股数组公式为,其中m>n>0,m、n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
4
参考答案
1.A
2.A
3.等腰直角三角形
4.B
5.13,84,85
6.解:(1)同位角相等,两直线平行,真命题;
(2)对应角相等的三角形全等,假命题;
(3)到线段的两个端点的距离相等的点在线段的垂直平分线上,真命题;
(4)如果2a是偶数,则a是偶数,假命题.
7.B
8.B
9.C
10.
11.两边上的高相等的三角形是等腰三角形
正确
12.解:在△ABD中,由122+52=132,可知AD2+BD2=AB2,所以△ABD为直角三角形且∠ADB=90°.在Rt△ADC中,DC==9.
13.解:连接AC.在Rt△ABC中,AB=3,BC=4,∴AC===5.又∵DC=12,AD=13,∴AD2=AC2+CD2,∴△ACD为直角三角形,∴S四边形ABCD=S△ABC+S△ACD=×3×4+×5×12=6+30=36.
14.解:因为票价与路程成正比,故可将票价视为路程来处理.因为AB=10,AD=8,BD=6,所以AD2+BD2=82+62=64+36=100=102=AB2,所以△ABD为直角三角形,且∠ADB=90°.连接BC,在Rt△BDC中,CD=4.5,BD=6,所以BC==7.5.故B、C之间公共汽车的票价为7.5元.
15.解:当n=1时,a=(m2-1),b=m,c=(m2+1),∵直角三角形有一边长为5,∴当a=5时,(m2-1)=5,m=±(舍去);当b=5时,m=5,则a=12,c=13;当c=5时,(m2+1)=5,m=±3,∵m>0,∴m=3,则a=4,b=3.综上所述,直角三角形的另外两条边长分别为12、13或3、4.
17.2 勾股定理的逆定理
1.(桂林中考)下列各组线段能构成直角三角形的一组是( )
A.30,40,50 B.7,12,13 C.5,9,12 D.3,4,6
2.在△ABC中,AB=12cm,BC=16cm,AC=20cm,则△ABC的面积是( )
A.96cm2 B.120cm2 C.160cm2 D.200cm2
3.已知a、b、c是△ABC的三边长,且满足关系式+|a-b|=0,则△ABC的形状为 .
4.下列各组数据中,是勾股数的为( )
A.1,, B.8,15,17 C.32,42,52 D.,,1
5.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出具有以上规律的第⑥组勾股数 .
6.写出下列各命题的逆命题,并判断逆命题的真假性:
(1)两直线平行,同位角相等;
(2)全等三角形的对应角相等;
(3)线段垂直平分线上的点到线段的两个端点的距离相等;
(4)如果a是偶数,则2a是偶数.
7.下列各组数中,不是勾股数的一组是( )
A.7,24,25 B.4,5,6 C.5,12,13 D.8,15,17
8.a、b、c是△ABC的∠A、∠B、∠C的对边,且a∶b∶c=1∶∶,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
9.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )
10.在△ABC中,a=5,b=6,当c= 时,∠C是直角;当c= 时,∠B是直角.
11.“等腰三角形两腰上的高相等”的逆命题是
,这个命题是 (填“正确”或“错误”)的.
12.如图,在△ABC中,D是BC边上的点,已知AB=13,AD=12,AC=15,BD=5,求DC的长.
13.如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13.求四边形ABCD的面积.
14.如图,A、B、C、D是四个小镇,它们之间(除B、C外)都有笔直的公路相连接,公共汽车行驶于城镇之间,其票价与路程成正比.已知各城镇间的公共汽车票价如下:A B:10元;A C:12.5元;A D:8元;B D:6元;C D:4.5元.为了B、C之间的交通方便,在B、C之间建成笔直公路,请按上述标准计算出B、C之间公共汽车的票价为多少元?
15.(宜昌中考)阅读:能够成为直角三角形三边长的三个正整数a、b、c称为勾股数,世界上第一次给出勾股数通解公式的是我国古代的数学著作《九章算术》,其勾股数组公式为,其中m>n>0,m、n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
4
参考答案
1.A
2.A
3.等腰直角三角形
4.B
5.13,84,85
6.解:(1)同位角相等,两直线平行,真命题;
(2)对应角相等的三角形全等,假命题;
(3)到线段的两个端点的距离相等的点在线段的垂直平分线上,真命题;
(4)如果2a是偶数,则a是偶数,假命题.
7.B
8.B
9.C
10.
11.两边上的高相等的三角形是等腰三角形
正确
12.解:在△ABD中,由122+52=132,可知AD2+BD2=AB2,所以△ABD为直角三角形且∠ADB=90°.在Rt△ADC中,DC==9.
13.解:连接AC.在Rt△ABC中,AB=3,BC=4,∴AC===5.又∵DC=12,AD=13,∴AD2=AC2+CD2,∴△ACD为直角三角形,∴S四边形ABCD=S△ABC+S△ACD=×3×4+×5×12=6+30=36.
14.解:因为票价与路程成正比,故可将票价视为路程来处理.因为AB=10,AD=8,BD=6,所以AD2+BD2=82+62=64+36=100=102=AB2,所以△ABD为直角三角形,且∠ADB=90°.连接BC,在Rt△BDC中,CD=4.5,BD=6,所以BC==7.5.故B、C之间公共汽车的票价为7.5元.
15.解:当n=1时,a=(m2-1),b=m,c=(m2+1),∵直角三角形有一边长为5,∴当a=5时,(m2-1)=5,m=±(舍去);当b=5时,m=5,则a=12,c=13;当c=5时,(m2+1)=5,m=±3,∵m>0,∴m=3,则a=4,b=3.综上所述,直角三角形的另外两条边长分别为12、13或3、4.
