2018~2019学年5月湖南长沙天心区明德天心中学初三下学期月考A卷数学试卷(含解析)
文档属性
| 名称 | 2018~2019学年5月湖南长沙天心区明德天心中学初三下学期月考A卷数学试卷(含解析) |  | |
| 格式 | |||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-25 09:46:30 | ||
图片预览



文档简介
2018~2019学年5月湖南长沙天心区明德天心中学初三下学期月考A卷数学
试卷
一、选择题(本大题共12题,每小题3分,共计36分。)
1、 等于( ).
A.
B.
C.
D.
2、下列计算正确的是( ).
A.
B.
C.
D.
3、我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划,“一带一路”地区覆盖总人口
为 人,这个数用科学记数法表示为( ).
A.
B.
C.
D.
4、如图,有一块含有 角的直角三角板的两个顶点放在直尺的对边上,如果 ,那么 的度数是(
).
A.
B.
C.
D.
5、下列说法正确的是( ).
A.“明天降雨的概率为 ”,意味着明天一定有半天都在降雨
B.了解全国快递包裹产生的包装垃圾数量适合采用全面调查(普查)方式
C.掷一枚质地均匀的骰子,骰子停止转动后, 点朝上是必然事件
D.一组数据的方差越大,则这组数据的波动也越大
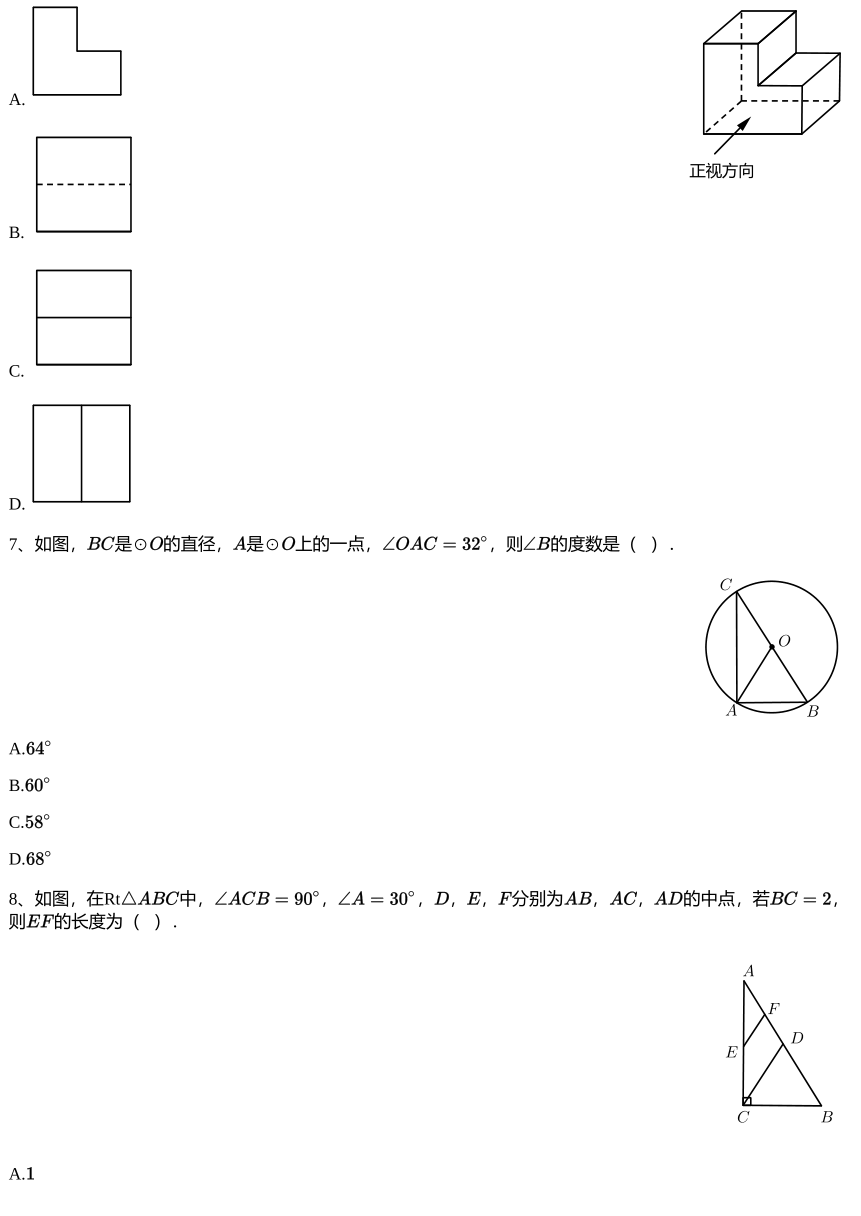
6、如图所示的几何体的左视图是( ).
A.
正视方向
B.
C.
D.
7、如图, 是⊙ 的直径, 是⊙ 上的一点, ,则 的度数是( ).
A.
B.
C.
D.
8、如图,在Rt 中, , , , , 分别为 , , 的中点,若 ,
则 的长度为( ).
A.
B.
C.
D.
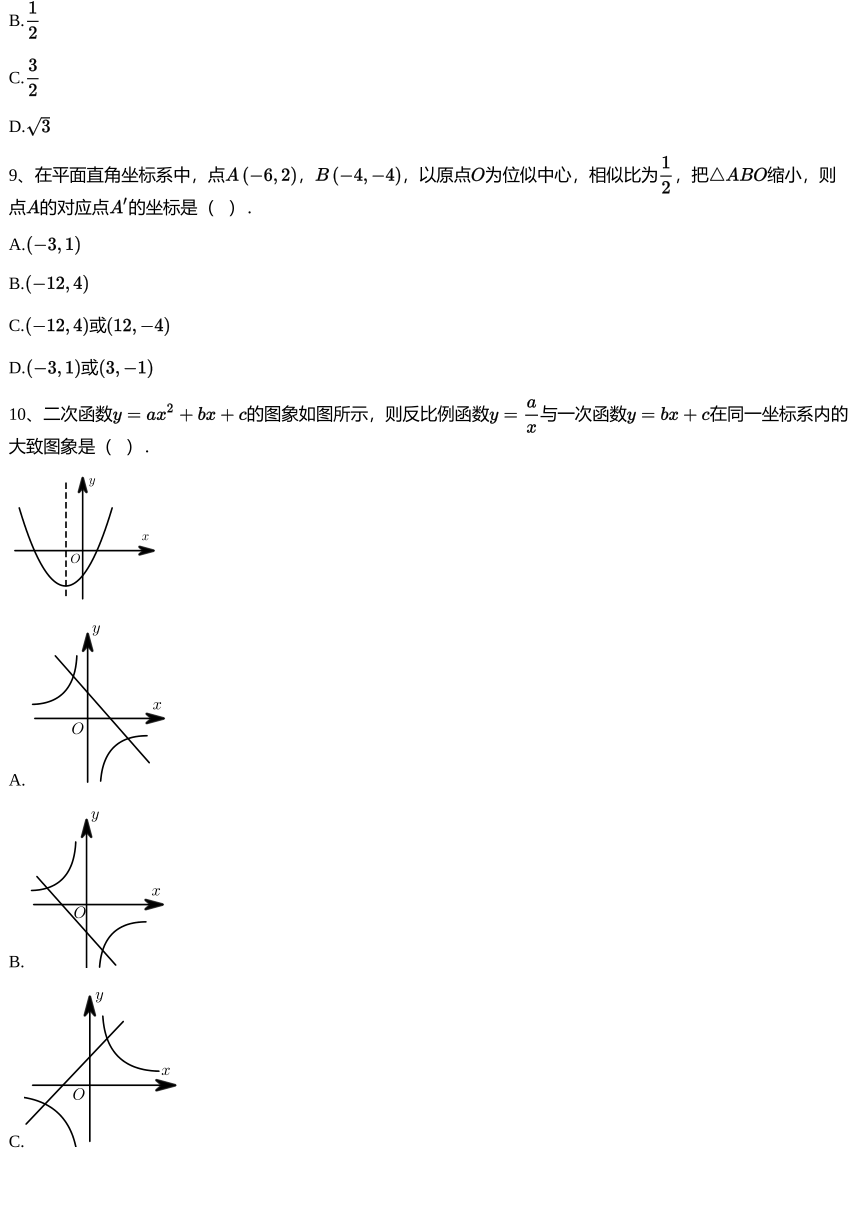
9、在平面直角坐标系中,点 , ,以原点 为位似中心,相似比为 ,把 缩小,则
点 的对应点 的坐标是( ).
A.
B.
C. 或
D. 或
10、二次函数 的图象如图所示,则反比例函数 与一次函数 在同一坐标系内的
大致图象是( ).
A.
B.
C.
D.
11、若点 , , 在双曲线 上,则 , , 的大小关系是( ).
A.
B.
C.
D.
12、如图,在正方形 中, 是等边三角形, 、 的延长线分别交 于点 、 ,连接 、
、 与 相交于点 ,给出下列结论:
① ;② ;③ ;④ ;⑤ ,其中正确
的是( ).
A.①②③④
B.①③④⑤
C.①②④⑤
D.②③④⑤
二、填空题(本大题共6题,每小题3分,共计18分。)
13、已知函数 ,则自变量 的取值范围是 .
14、因式分解: .
15、若正多边形的每一个外角为 ,则这个正多边形的边数是 .
16、圆锥的底面半径为 cm,母线长为 cm,则这个圆锥的侧面积是 .
17、如图,正方形 的边长为 ,点 在边 上, , 两点关于对角线 对称,若 ,则
.
18、如图,反比例函数 的图象经过平行四边形 对角线的交点 ,已知点 , ,
在坐标轴上, ,平行四边形 的面积为 ,则 .
y
O x
三、解答题(本大题共8题,共计66分。)
19、计算: .
20、先化简,再求值: ,请选择一个适当的数代入求值.
21、某中学为了解学生对新闻、体育、娱乐、动画四类电视节目的喜爱情况,进行了统计调查.随机调查了某
班所有同学最喜欢的节目(每名学生必选且只能选择四类节目中的一类)并将调查结果绘成如下不完整的统计
图.,根据两图提供的信息,回答下列问题:
新闻 学生人数
娱乐
体育
动画
新闻 体育 娱乐 动画 节目类型
(1)、最喜欢娱乐类节目的有 人,图中 .
(2)、请补全条形统计图.
(3)、在全班同学中,有甲、乙、丙、丁等同学最喜欢体育类节目,班主任打算从甲、乙、丙、丁 名同学中选
取 人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲、乙两同学的概率.
22、如图,为了测量山坡上一棵树 的高度,小明在点 处利用测角仪测得树顶 的仰角为 ,然后他沿着
正对树 的方向前进 m到达点 处,此时测得树顶 和树底 的仰角分别是 和 ,设 垂直于 ,且
垂足为 .
(1)、求 的度数.
(2)、求树 的高度(结果精确到 m, ).
23、某文具店购进一批纪念册,每本进价为 元,出于营销考虑,要求每本纪念册的售价不低于 元且不高于
元,在销售过程中发现该纪念册每周的销售量 (本)与每本纪念册的售价 (元)之间满足一次函数关系且
为正整数:当销售单价为 元时,销售量为 本;当销售单价为 元时,销售量为 本.
(1)、求出 与 的函数关系式.
(2)、当文具店每周销售这种纪念册获得 元的利润时,每本纪念册的销售单价是多少元?
(3)、设该文具店每周销售这种纪念册所获得的利润为 元,将该纪念册销售单价定为多少元时,才能使文具店
每周销售该纪念册所获利润最大?最大利润是多少?
24、如图, 是⊙ 的直径,点 , 在⊙ 上, ,点 在 的延长线上, .
(1)、求证: 是⊙ 的切线.
(2)、连接 ,求证: .
(3)、若 , ,求⊙ 的半径长.
25、如图,在平面直角坐标系中,分别过曲线段 的两个端点作 轴的垂线交 轴
于点 、 ,我们把线段 叫做曲线段 在 轴上的“射影”,线段 的长
度叫做曲线段 在 轴上的“射影长度”,在 轴上的“射影范围”为点 、 横坐标之间的范围;同理,分别过
曲线段 的两个端点作 轴的垂线交 轴于点 、 ,我们把线段 叫曲线段 在 轴上的“射影”,例
如,若图中 , 在 轴上的“射影”分别 , ,则曲线段 在 轴上的“射影长
度”为 ,在 轴上的“射影范围”为 .
(1)、反比例函数 的部分图像在 轴上的“射影范围”为 ,求此时在 轴上的“射影长度”.
(2)、当 时,若二次函数 的部分图象在 轴的“射影范围”为 时,在 轴上
的“射影”最高点为 ,求 的值.
(3)、二次函数 ,其中 ,与一次函数 的交点为 、 ,求线
段 在 轴上的“射影长度”的取值范围.
26、如图 ,在平面直角坐标系中,抛物线 经过 , , ,顶点为 .
图
(1)、求抛物线的解析式.
(2)、假设点 是直线 上方抛物线上一动点,过点 作 ,求当 取得最大值时,点 的坐标.
(3)、连接 、 、 ,设 沿 轴正方向平移 个单位长度( )时, 与 重叠部
分的面积为 ,求 与 之间的函数关系式,并指出 的取值范围.
备用图 备用图
参考答案
一、选择题
1、
【答案】
A
【分析】
.
故选A.
2、
【答案】
D
【分析】
,A错误;
,B错误;
,C错误;
,D正确;
故选:D.
3、
【答案】
C
【分析】
.
4、
【答案】
B
【分析】
如图:
∵ ,
∴ ,
∵ ,
∴ ,
∴ .
故选:B.
5、
【答案】
D
【分析】
略
6、
【答案】
B
【分析】
从左边观察几何体,能够看到的线用实线,看不到的线用虚线,所以图中几何体左视图应选B.
故选B.
7、
【答案】
C
【分析】
∵ ,
∴ ,
∵ 是直径,
∴ .
故选C.
8、
【答案】
A
【分析】
∵ , 为 的中点,
∴ ,
∵ , ,
∴ ,
∴ 是等边三角形,
∴ ,
∵ , 分别为 , 的中点,
∴ .
故选A.
9、
【答案】
D
【分析】
∵ 的一个顶点 的坐标是 ,
以原点 为位似中心,相似比为 ,
将 缩小得到它的位似图形 ,
∴点 的坐标是 或 ,
即 或 ,
故选D.
10、
【答案】
D
【分析】
∵二次函数的图象开口向上,即 ,
∴反比例函数 的图象必在第一、三象限,故A,B错误,
∵二次函数的图象与 轴交点的纵坐标小于 ,
∴ ,
∴一次函数 的图象与 轴的交点必在 轴下方,故C错误,D正确.
故选D.
11、
【答案】
C
【分析】
∵ ,
∴ 的图象必经过二、四象限.
∵点 , , 在双曲线 上,
∴ , 分布在第二象限,
在第四象限,每个象限内,
随 的增大而增大,
∴ .
故选C.
12、
【答案】
B
【分析】
①∵ 是等边三角形,
∴ , ,
在正方形 中,
∵ , ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,故①正确;
②∵ , ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,故②错误;
③∵ ,
,
又∵ ,
∴ ,
∴ ,故③正确;
④∵ ,
又 ,
∴ ,
∴ ,
∵ ,
∴ ,故④正确;
⑤如图,过 作 , ,设正方形 的边长是 , 为正三角形,
∴ , ,
∴ ,
∴ ,
,
∵ ,
∴ ,
∴ ,
∴
,故⑤正确;
故答案为:①③④⑤.
故选:B.
二、填空题
13、
【答案】
且
【分析】
∵ ,
∴ ,
解得 ,
∴自变量 的取值范围是 且 .
14、
【答案】
【分析】
.
15、
【答案】
【分析】
∵正多边形外角和为 ,
∴正多边形边数为 ,
故答案为: .
16、
【答案】
cm
【分析】
圆锥的侧面积 底面周长 母线长 ,
∵底面半径为 cm,
∴底面周长为 cm,
∴侧面积 cm .
故答案为: cm .
17、
【答案】
【分析】
在正方形 中, ,
∵ ,
∴ ,
∵ , 两点关于对角线 对称,
∴ ,
∵ ,
∴ ,
∵ ,
∴ .
18、
【答案】
【分析】
连接 ,
y
O x
∵四边形 是平行四边形,
∴ , , , ,
∵ ,
∴ ,
∴四边形 是矩形,
∴ ,
∵ 平行四边形 ,
∴ ,
∴ ,
∵ ,
∴ .
故答案为: .
三、解答题
19、
【答案】
.
【分析】
.
20、
【答案】
; 时,原式 .
【分析】
原式
,
∵ ,
∴ ,
把 代入得 .
21、
【答案】
(1)、 ;
(2)、
画图见解析.
(3)、
.
【分析】
(1)、∵被调查的总人数为 (人),
∴最喜欢娱乐类节目的有 (人),
,即 ,
故答案为: , .
(2)、补全条形统计图如下:
学生人数
新闻 体育 娱乐 动画 节目类型
(3)、画树状图得:
开始
甲 乙 丙 丁
乙丙 丁 甲 丙 丁 甲 乙丁 甲 乙 丙
∵共有 种等可能的结果,恰好同时选中甲、乙两位同学的有 种情况,
∴恰好同时选中甲、乙两位同学的概率为 .
22、
【答案】
(1)、
.
(2)、
米.
【分析】
(1)、∵ ,
∴ ,
∵ ,
∴ .
(2)、设 m,
∵ , ,
∴ m, m,
∵ ,
∴ m,
∴ m,
∵ ,
∴ 是等腰直角三角形,
∴ m,
∵ m,
∴ ,
解得: (米),
∴ (米),
故树 的高度约为 米.
23、
【答案】
(1)、
.( , 为整数)
(2)、
.
(3)、
将该纪念册销售单价定为 元时,才能使文具店每周销售该纪念册所获利润最大,最大利润是 元.
【分析】
(1)、设 ,
把 与 代入得: ,
解得: ,
则 .
(2)、设当文具店每周销售这种纪念册获得 元的利润时,每本纪念册的销售单价是 元,
根据题意得: ,
则 ,
整理得: ,
,
解得: , (不合题意舍去),
答:每本纪念册的销售单价是 元.
(3)、由题意可得:
,
此时当 时, 最大,
又 售价不低于 元且不高于 元,
时, 随 的增大而增大,即当 时, 最大 (元).
答:该纪念册销售单价定为 元时,才能使文具店每周销售该纪念册所获利润最大,最大利润是 元.
24、
【答案】
(1)、
证明见解析.
(2)、
证明见解析.
(3)、
.
【分析】
(1)、连接 ,
则 ,
又∵ ,
∴ ,
∵ , ,
∴ ,
∴ ,
又∵ 是直径,
∴ ,
∴ 与 相切.
(2)、连接 , ,
∵ 与 是同弧所对的圆周角,
∴ ,
∵ 是 的直径,
∴ , ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ .
(3)、连接 ,
则 ,
∵ ,
∴ ,
在 和 中,
, ,
∴ ,
∴ ,则 ,
∵ ,
∴ ,
∴ ,
∵ , ,
∴ ,
∴ .
25、
【答案】
(1)、
.
(2)、
.
(3)、
.
【分析】
(1)、反比例函数 在第一象限内随 随 增大而减小,
∴为 时, ,当 时, ,
∴当 时, ,
∴此时在 轴的“射影长度”为 .
(2)、当 时,二次函数 ,
∴二次函数的对称轴为直线 ,
∵二次函数在 轴的“射影范围”为 时,在 轴的“射影”最高点为 ,
∴当 时,二次函数 的最大值为 ,根据题意,分两种情况讨论.
当 时,在 时,二次函数取最大值,即 不成立,
当 时,在 时,二次函数取最大值,即 .
所以, ,解得, , (舍去).
综上可得, .
(3)、设 , 两点坐标分别为 、 ,则 , 是一元二次方程, 的
两个根,
所以, , , , 可知, , , ,
∴ ,
因此, ,
所以 .
设线段 在 轴的“射影长度”为 ,则
.
所以,当 时, .
26、
【答案】
(1)、
.
(2)、
.
(3)、
.
【分析】
(1)、由题意得,设抛物线解析式为 ,
将 代入上式, ,
解得 ,
∴ .
(2)、如图 ,
图
∵ , , ,
∴ ,
即 是等腰直角三角形,且珍惜 的解析式为: ,
过点 作 轴,交 于点 ,则有 轴,
∴ ,
∴ ,
设 ,则 ,
∴ ,
∵ ,
∴当 时, .取得最大值,即 取得最大值,
此时,点 的坐标为 .
(3)、设直线 的解析式为 ,
将 , 代入,得 ,
解得 ,
则直线 的解析式为 ,
过 点作射线 轴交 于点 ,
当 时,得 ,
故 ,
情况一:如图 ,
图
当 时,设 平移到 的位置, 交 于点 , 交 于点 ,
则 ,
过点 作 轴于点 ,交 于点 ,
由 ,得 ,即 ,
解得: ,
∴ 阴
,
情况二:如图 ,
图
当 时,
设 平移到 的位置,
交 于点 ,交 于点 ,
由 ,得 ,即 ,
解得: ,
∴ 阴
,
综上所述: .
试卷
一、选择题(本大题共12题,每小题3分,共计36分。)
1、 等于( ).
A.
B.
C.
D.
2、下列计算正确的是( ).
A.
B.
C.
D.
3、我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划,“一带一路”地区覆盖总人口
为 人,这个数用科学记数法表示为( ).
A.
B.
C.
D.
4、如图,有一块含有 角的直角三角板的两个顶点放在直尺的对边上,如果 ,那么 的度数是(
).
A.
B.
C.
D.
5、下列说法正确的是( ).
A.“明天降雨的概率为 ”,意味着明天一定有半天都在降雨
B.了解全国快递包裹产生的包装垃圾数量适合采用全面调查(普查)方式
C.掷一枚质地均匀的骰子,骰子停止转动后, 点朝上是必然事件
D.一组数据的方差越大,则这组数据的波动也越大
6、如图所示的几何体的左视图是( ).
A.
正视方向
B.
C.
D.
7、如图, 是⊙ 的直径, 是⊙ 上的一点, ,则 的度数是( ).
A.
B.
C.
D.
8、如图,在Rt 中, , , , , 分别为 , , 的中点,若 ,
则 的长度为( ).
A.
B.
C.
D.
9、在平面直角坐标系中,点 , ,以原点 为位似中心,相似比为 ,把 缩小,则
点 的对应点 的坐标是( ).
A.
B.
C. 或
D. 或
10、二次函数 的图象如图所示,则反比例函数 与一次函数 在同一坐标系内的
大致图象是( ).
A.
B.
C.
D.
11、若点 , , 在双曲线 上,则 , , 的大小关系是( ).
A.
B.
C.
D.
12、如图,在正方形 中, 是等边三角形, 、 的延长线分别交 于点 、 ,连接 、
、 与 相交于点 ,给出下列结论:
① ;② ;③ ;④ ;⑤ ,其中正确
的是( ).
A.①②③④
B.①③④⑤
C.①②④⑤
D.②③④⑤
二、填空题(本大题共6题,每小题3分,共计18分。)
13、已知函数 ,则自变量 的取值范围是 .
14、因式分解: .
15、若正多边形的每一个外角为 ,则这个正多边形的边数是 .
16、圆锥的底面半径为 cm,母线长为 cm,则这个圆锥的侧面积是 .
17、如图,正方形 的边长为 ,点 在边 上, , 两点关于对角线 对称,若 ,则
.
18、如图,反比例函数 的图象经过平行四边形 对角线的交点 ,已知点 , ,
在坐标轴上, ,平行四边形 的面积为 ,则 .
y
O x
三、解答题(本大题共8题,共计66分。)
19、计算: .
20、先化简,再求值: ,请选择一个适当的数代入求值.
21、某中学为了解学生对新闻、体育、娱乐、动画四类电视节目的喜爱情况,进行了统计调查.随机调查了某
班所有同学最喜欢的节目(每名学生必选且只能选择四类节目中的一类)并将调查结果绘成如下不完整的统计
图.,根据两图提供的信息,回答下列问题:
新闻 学生人数
娱乐
体育
动画
新闻 体育 娱乐 动画 节目类型
(1)、最喜欢娱乐类节目的有 人,图中 .
(2)、请补全条形统计图.
(3)、在全班同学中,有甲、乙、丙、丁等同学最喜欢体育类节目,班主任打算从甲、乙、丙、丁 名同学中选
取 人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲、乙两同学的概率.
22、如图,为了测量山坡上一棵树 的高度,小明在点 处利用测角仪测得树顶 的仰角为 ,然后他沿着
正对树 的方向前进 m到达点 处,此时测得树顶 和树底 的仰角分别是 和 ,设 垂直于 ,且
垂足为 .
(1)、求 的度数.
(2)、求树 的高度(结果精确到 m, ).
23、某文具店购进一批纪念册,每本进价为 元,出于营销考虑,要求每本纪念册的售价不低于 元且不高于
元,在销售过程中发现该纪念册每周的销售量 (本)与每本纪念册的售价 (元)之间满足一次函数关系且
为正整数:当销售单价为 元时,销售量为 本;当销售单价为 元时,销售量为 本.
(1)、求出 与 的函数关系式.
(2)、当文具店每周销售这种纪念册获得 元的利润时,每本纪念册的销售单价是多少元?
(3)、设该文具店每周销售这种纪念册所获得的利润为 元,将该纪念册销售单价定为多少元时,才能使文具店
每周销售该纪念册所获利润最大?最大利润是多少?
24、如图, 是⊙ 的直径,点 , 在⊙ 上, ,点 在 的延长线上, .
(1)、求证: 是⊙ 的切线.
(2)、连接 ,求证: .
(3)、若 , ,求⊙ 的半径长.
25、如图,在平面直角坐标系中,分别过曲线段 的两个端点作 轴的垂线交 轴
于点 、 ,我们把线段 叫做曲线段 在 轴上的“射影”,线段 的长
度叫做曲线段 在 轴上的“射影长度”,在 轴上的“射影范围”为点 、 横坐标之间的范围;同理,分别过
曲线段 的两个端点作 轴的垂线交 轴于点 、 ,我们把线段 叫曲线段 在 轴上的“射影”,例
如,若图中 , 在 轴上的“射影”分别 , ,则曲线段 在 轴上的“射影长
度”为 ,在 轴上的“射影范围”为 .
(1)、反比例函数 的部分图像在 轴上的“射影范围”为 ,求此时在 轴上的“射影长度”.
(2)、当 时,若二次函数 的部分图象在 轴的“射影范围”为 时,在 轴上
的“射影”最高点为 ,求 的值.
(3)、二次函数 ,其中 ,与一次函数 的交点为 、 ,求线
段 在 轴上的“射影长度”的取值范围.
26、如图 ,在平面直角坐标系中,抛物线 经过 , , ,顶点为 .
图
(1)、求抛物线的解析式.
(2)、假设点 是直线 上方抛物线上一动点,过点 作 ,求当 取得最大值时,点 的坐标.
(3)、连接 、 、 ,设 沿 轴正方向平移 个单位长度( )时, 与 重叠部
分的面积为 ,求 与 之间的函数关系式,并指出 的取值范围.
备用图 备用图
参考答案
一、选择题
1、
【答案】
A
【分析】
.
故选A.
2、
【答案】
D
【分析】
,A错误;
,B错误;
,C错误;
,D正确;
故选:D.
3、
【答案】
C
【分析】
.
4、
【答案】
B
【分析】
如图:
∵ ,
∴ ,
∵ ,
∴ ,
∴ .
故选:B.
5、
【答案】
D
【分析】
略
6、
【答案】
B
【分析】
从左边观察几何体,能够看到的线用实线,看不到的线用虚线,所以图中几何体左视图应选B.
故选B.
7、
【答案】
C
【分析】
∵ ,
∴ ,
∵ 是直径,
∴ .
故选C.
8、
【答案】
A
【分析】
∵ , 为 的中点,
∴ ,
∵ , ,
∴ ,
∴ 是等边三角形,
∴ ,
∵ , 分别为 , 的中点,
∴ .
故选A.
9、
【答案】
D
【分析】
∵ 的一个顶点 的坐标是 ,
以原点 为位似中心,相似比为 ,
将 缩小得到它的位似图形 ,
∴点 的坐标是 或 ,
即 或 ,
故选D.
10、
【答案】
D
【分析】
∵二次函数的图象开口向上,即 ,
∴反比例函数 的图象必在第一、三象限,故A,B错误,
∵二次函数的图象与 轴交点的纵坐标小于 ,
∴ ,
∴一次函数 的图象与 轴的交点必在 轴下方,故C错误,D正确.
故选D.
11、
【答案】
C
【分析】
∵ ,
∴ 的图象必经过二、四象限.
∵点 , , 在双曲线 上,
∴ , 分布在第二象限,
在第四象限,每个象限内,
随 的增大而增大,
∴ .
故选C.
12、
【答案】
B
【分析】
①∵ 是等边三角形,
∴ , ,
在正方形 中,
∵ , ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,故①正确;
②∵ , ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,故②错误;
③∵ ,
,
又∵ ,
∴ ,
∴ ,故③正确;
④∵ ,
又 ,
∴ ,
∴ ,
∵ ,
∴ ,故④正确;
⑤如图,过 作 , ,设正方形 的边长是 , 为正三角形,
∴ , ,
∴ ,
∴ ,
,
∵ ,
∴ ,
∴ ,
∴
,故⑤正确;
故答案为:①③④⑤.
故选:B.
二、填空题
13、
【答案】
且
【分析】
∵ ,
∴ ,
解得 ,
∴自变量 的取值范围是 且 .
14、
【答案】
【分析】
.
15、
【答案】
【分析】
∵正多边形外角和为 ,
∴正多边形边数为 ,
故答案为: .
16、
【答案】
cm
【分析】
圆锥的侧面积 底面周长 母线长 ,
∵底面半径为 cm,
∴底面周长为 cm,
∴侧面积 cm .
故答案为: cm .
17、
【答案】
【分析】
在正方形 中, ,
∵ ,
∴ ,
∵ , 两点关于对角线 对称,
∴ ,
∵ ,
∴ ,
∵ ,
∴ .
18、
【答案】
【分析】
连接 ,
y
O x
∵四边形 是平行四边形,
∴ , , , ,
∵ ,
∴ ,
∴四边形 是矩形,
∴ ,
∵ 平行四边形 ,
∴ ,
∴ ,
∵ ,
∴ .
故答案为: .
三、解答题
19、
【答案】
.
【分析】
.
20、
【答案】
; 时,原式 .
【分析】
原式
,
∵ ,
∴ ,
把 代入得 .
21、
【答案】
(1)、 ;
(2)、
画图见解析.
(3)、
.
【分析】
(1)、∵被调查的总人数为 (人),
∴最喜欢娱乐类节目的有 (人),
,即 ,
故答案为: , .
(2)、补全条形统计图如下:
学生人数
新闻 体育 娱乐 动画 节目类型
(3)、画树状图得:
开始
甲 乙 丙 丁
乙丙 丁 甲 丙 丁 甲 乙丁 甲 乙 丙
∵共有 种等可能的结果,恰好同时选中甲、乙两位同学的有 种情况,
∴恰好同时选中甲、乙两位同学的概率为 .
22、
【答案】
(1)、
.
(2)、
米.
【分析】
(1)、∵ ,
∴ ,
∵ ,
∴ .
(2)、设 m,
∵ , ,
∴ m, m,
∵ ,
∴ m,
∴ m,
∵ ,
∴ 是等腰直角三角形,
∴ m,
∵ m,
∴ ,
解得: (米),
∴ (米),
故树 的高度约为 米.
23、
【答案】
(1)、
.( , 为整数)
(2)、
.
(3)、
将该纪念册销售单价定为 元时,才能使文具店每周销售该纪念册所获利润最大,最大利润是 元.
【分析】
(1)、设 ,
把 与 代入得: ,
解得: ,
则 .
(2)、设当文具店每周销售这种纪念册获得 元的利润时,每本纪念册的销售单价是 元,
根据题意得: ,
则 ,
整理得: ,
,
解得: , (不合题意舍去),
答:每本纪念册的销售单价是 元.
(3)、由题意可得:
,
此时当 时, 最大,
又 售价不低于 元且不高于 元,
时, 随 的增大而增大,即当 时, 最大 (元).
答:该纪念册销售单价定为 元时,才能使文具店每周销售该纪念册所获利润最大,最大利润是 元.
24、
【答案】
(1)、
证明见解析.
(2)、
证明见解析.
(3)、
.
【分析】
(1)、连接 ,
则 ,
又∵ ,
∴ ,
∵ , ,
∴ ,
∴ ,
又∵ 是直径,
∴ ,
∴ 与 相切.
(2)、连接 , ,
∵ 与 是同弧所对的圆周角,
∴ ,
∵ 是 的直径,
∴ , ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ .
(3)、连接 ,
则 ,
∵ ,
∴ ,
在 和 中,
, ,
∴ ,
∴ ,则 ,
∵ ,
∴ ,
∴ ,
∵ , ,
∴ ,
∴ .
25、
【答案】
(1)、
.
(2)、
.
(3)、
.
【分析】
(1)、反比例函数 在第一象限内随 随 增大而减小,
∴为 时, ,当 时, ,
∴当 时, ,
∴此时在 轴的“射影长度”为 .
(2)、当 时,二次函数 ,
∴二次函数的对称轴为直线 ,
∵二次函数在 轴的“射影范围”为 时,在 轴的“射影”最高点为 ,
∴当 时,二次函数 的最大值为 ,根据题意,分两种情况讨论.
当 时,在 时,二次函数取最大值,即 不成立,
当 时,在 时,二次函数取最大值,即 .
所以, ,解得, , (舍去).
综上可得, .
(3)、设 , 两点坐标分别为 、 ,则 , 是一元二次方程, 的
两个根,
所以, , , , 可知, , , ,
∴ ,
因此, ,
所以 .
设线段 在 轴的“射影长度”为 ,则
.
所以,当 时, .
26、
【答案】
(1)、
.
(2)、
.
(3)、
.
【分析】
(1)、由题意得,设抛物线解析式为 ,
将 代入上式, ,
解得 ,
∴ .
(2)、如图 ,
图
∵ , , ,
∴ ,
即 是等腰直角三角形,且珍惜 的解析式为: ,
过点 作 轴,交 于点 ,则有 轴,
∴ ,
∴ ,
设 ,则 ,
∴ ,
∵ ,
∴当 时, .取得最大值,即 取得最大值,
此时,点 的坐标为 .
(3)、设直线 的解析式为 ,
将 , 代入,得 ,
解得 ,
则直线 的解析式为 ,
过 点作射线 轴交 于点 ,
当 时,得 ,
故 ,
情况一:如图 ,
图
当 时,设 平移到 的位置, 交 于点 , 交 于点 ,
则 ,
过点 作 轴于点 ,交 于点 ,
由 ,得 ,即 ,
解得: ,
∴ 阴
,
情况二:如图 ,
图
当 时,
设 平移到 的位置,
交 于点 ,交 于点 ,
由 ,得 ,即 ,
解得: ,
∴ 阴
,
综上所述: .
同课章节目录
