期末易错点检测卷-2023-2024学年数学九年级上册浙教版(含解析)
文档属性
| 名称 | 期末易错点检测卷-2023-2024学年数学九年级上册浙教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 20:29:27 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末易错点检测卷-2023-2024学年数学九年级上册浙教版
一、单选题
1.下列事件中,是必然事件的是( )
A.从一副扑克牌中到红桃 B.打开电视,正在播放新闻
C.两个无理数的积是无理 D.三角形的内角和为
2.下列关于二次函数的图象和性质的说法中,正确的是( )
A.图象开口向上 B.对称轴是直线
C.顶点坐标是 D.在此函数图象上
3.下列函数中,当时,随的增大而减小的是( )
A. B. C. D.
4.如图,将一个含角的直角三角板绕点A顺时针旋转,点C的对应点为点,若点落在延长线上,则旋转角的度数是( )
A. B. C. D.
5.如图,是的弦,是的直径,已知,,连接,若D是的中点,则的长( )
A. B. C. D.
6.如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
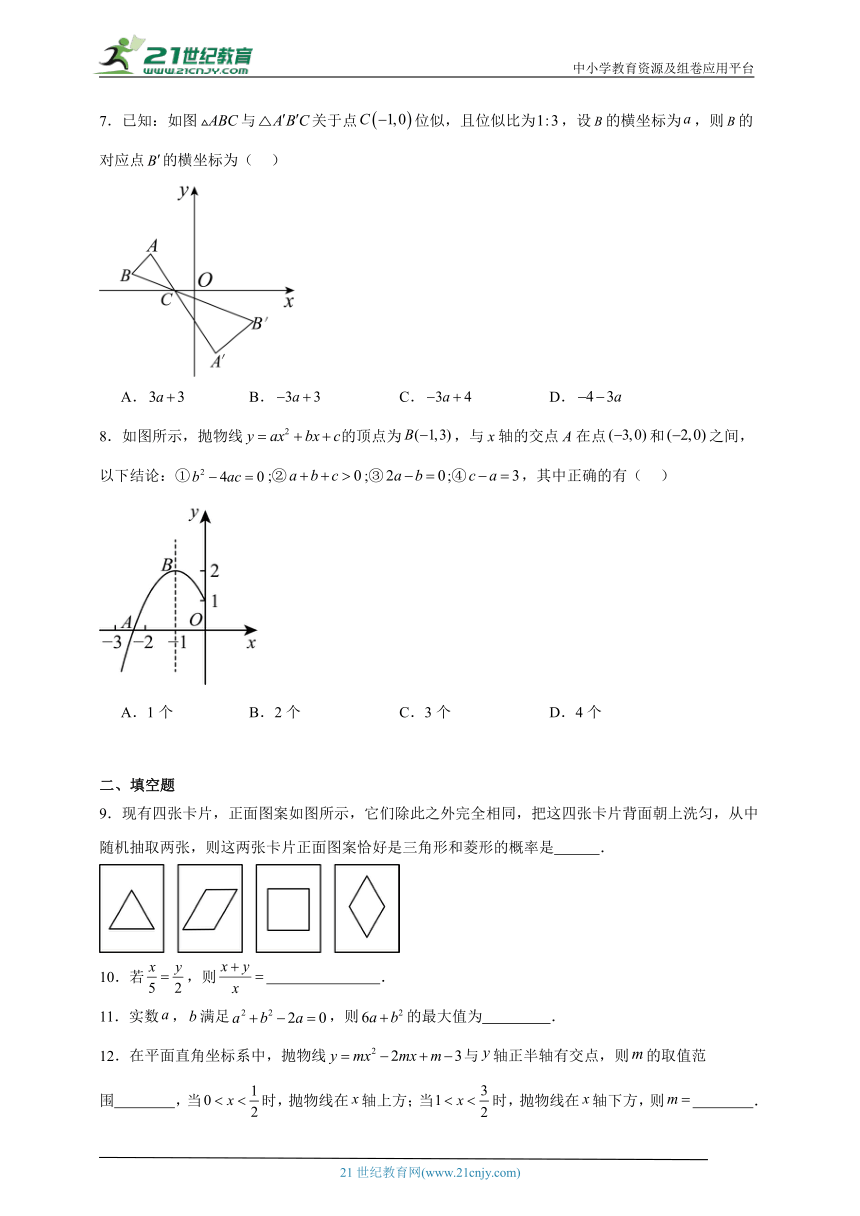
7.已知:如图与关于点位似,且位似比为,设的横坐标为,则的对应点的横坐标为( )
A. B. C. D.
8.如图所示,抛物线的顶点为,与x轴的交点A在点和之间,以下结论:①;②;③;④,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.现有四张卡片,正面图案如图所示,它们除此之外完全相同,把这四张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面图案恰好是三角形和菱形的概率是 .
10.若,则 .
11.实数,满足,则的最大值为 .
12.在平面直角坐标系中,抛物线与轴正半轴有交点,则的取值范围 ,当时,抛物线在轴上方;当时,抛物线在轴下方,则 .
13.如图,二次函数与一次函数的图象相交于两点,则关于的方程的解为 .
14.如图,是的直径,,点M在上,,N是弧的中点,P是直径上的一动点.若,则周长的最小值为 .
15.如图,在矩形中,,,是的中点,连接,P是边上一动点,过点P的直线将矩形折叠,使点D落在上的处,当是以为腰的等腰三角形时,
16.如图,扇形中,,,点C为上一点,将扇形沿折叠,使点B的对应点落在射线上,则图中阴影部分的面积为 .
三、解答题
17.“这么近,那么美,周末到河北.”越来越多的外地游客利用假期来领略河北优美的自然风光和厚重的历史文化.保定市莲池区某中学组建了一支学生讲解员队伍,到下面四个景区志愿服务.
景区有:直隶总督署—用A表示;古莲花池—用B表示;淮军公所—用C表示;保定军校博物馆—用D表示,
将编号A,B,C,D分别写在四张卡片上,每名同学随机抽取一张后放回,并到其抽到的景区志愿服务.
(1)小明抽到“直隶总督署”志愿服务的概率是__________.
(2)小明和小亮是同班同学,求他们抽到同一景区志愿服务的概率.(请用树状图或列表的方法写出分析过程)
18.在平面直角坐标系中,有抛物线.
(1)若点在抛物线上,
①求抛物线的对称轴;
②若点也在抛物线上,求a的取值范围;
(2)当时,有已知点,若抛物线与线段只有一个公共点,结合函数图象,求b的取值范围.
19.如图,四边形内接于,E为延长线上一点,连接,若.求证:平分.
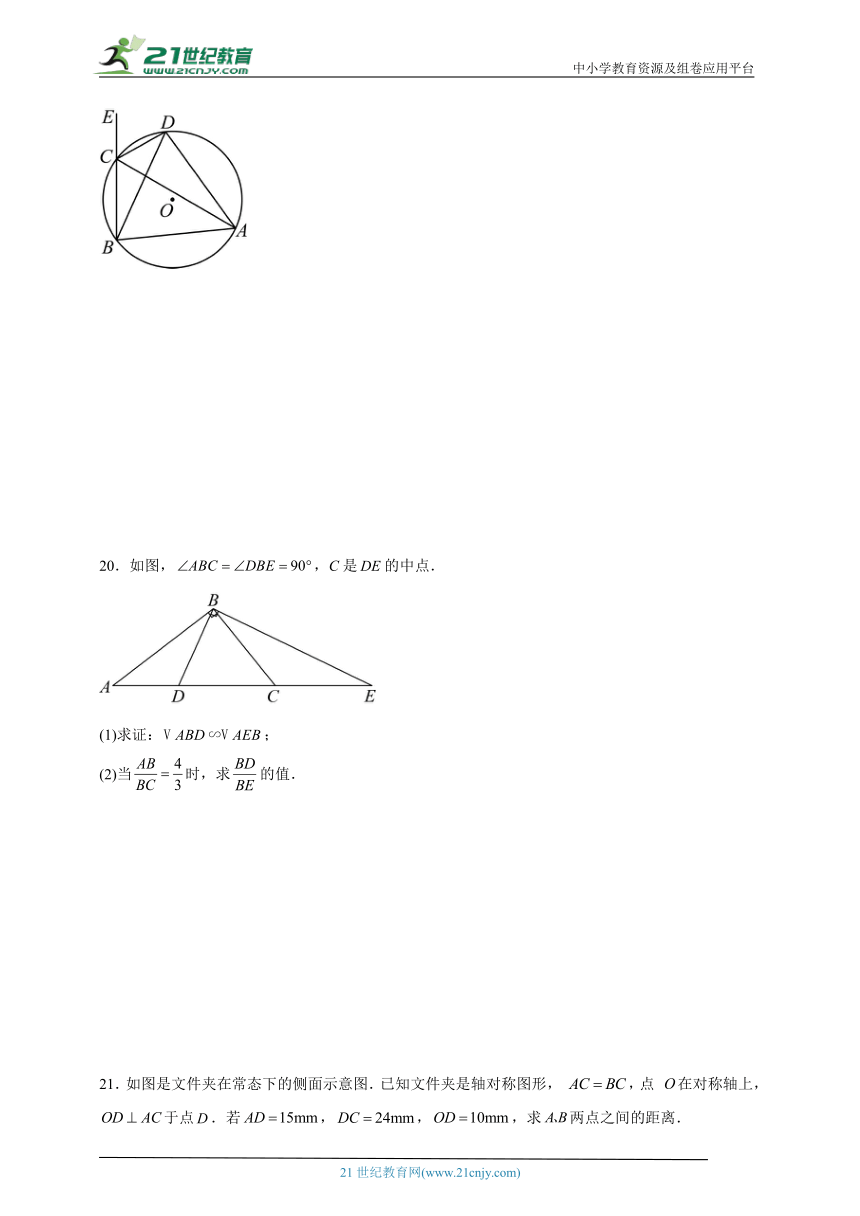
20.如图,,C是的中点.
(1)求证:;
(2)当时,求的值.
21.如图是文件夹在常态下的侧面示意图.已知文件夹是轴对称图形, ,点 在对称轴上,于点.若,,,求两点之间的距离.
22.二次函数的图象如图所示,根据图象解答下列问题.
(1)写出方程的两个根
(2)写出不等式的解集
(3)写出随的增大而减小的自变量的取值范围.
(4)若方程有两个不相等的实数根,直接写出的取值范围.
23.已知,在中,弦、相交于E,点C是的中点.
(1)如图1,当是直径时,求证:;
(2)如图2,当时,求证:;
(3)如图3,在(2)的条件下,连接,作直径,连接并延长交的延长线于G,,,求的半径长.
24.已知点M为二次函数图象的顶点,直线与轴、轴交于两点.
(1)如图1,若二次函数的图象也过点,
①求抛物线的解析式;
②若,根据图象直接写出x的范围;
(2)判断顶点M是否在直线上,并说明理由;
(3)如图2,点A的坐标为点M在内,若点都在二次函数图象上,试比较与的大小.
参考答案:
1.D
【分析】本题考查了必然事件和随机事件的定义,无理数的乘积,三角形内角和定理,理解“对于一个事件,有可能发生也有可能不发生,这个事件叫做随机事件;对于一个事件,一定会发生,这个事件叫做必然事件.”是解题的关键.
【详解】解:A.从一副扑克牌中到红桃是随机事件,不符合题意;
B.打开电视,正在播放新闻是随机事件,不符合题意;
C.两个无理数的积是无理是随机事件,不符合题意;
D.三角形的内角和为是必然事件,故符合题意;
故选:D.
2.D
【分析】本题考查了二次函数的图象与性质,熟练掌握二次函数的图象与性质是解答本题的关键.
根据二次函数的图象与性质对每一个选项进行分析,只有选项符合题意.
【详解】解:根据题意得:
、,图像开口向下,本选项说法不正确,故不符合题意;
、,对称轴是直线,本选项说法不正确,故不符合题意;
、,,顶点坐标为,本选项说法不正确,故不符合题意;
、当时,,在此函数图象上,本选项说法正确,故符合题意.
故选:.
3.B
【分析】本题主要考查反比例函数、二次函数、正比例函数图像的性质,根据各函数的解析式,逐项分析判断,即可求解.
【详解】解:A、正比例函数的图像,随的增大而增大,
故此选项不符合题意;
B、反比例函数的图像,当时,随的增大而减小,
故此选项符合题意;
C、二次函数的图像,开口向上,对称轴为轴,
当时,y随x的增大而增大,故此选项不符合题意;
D、反比例函数的图像,,当时,随的增大而增大,故此选项不符合题意;
故选:B.
4.D
【分析】本题主要考查旋转的性质,根据旋转角的定义,两对应边的夹角就是旋转角,即可求解.
【详解】解:∵将一个含角的直角三角板绕点A逆时针旋转,点C的对应点为点,若点落在BA延长线上,
∴旋转角是.
故选:D.
5.B
【分析】本题考查圆周角定理,含角的直角三角形的性质,三角形的中位线定理,证明为的中位线是解题的关键,属于中考常考题型.
由直径所对的圆周角是直角得,根据含角的直角三角形的性质得,证明是的中位线,由三角形的中位线定理即可求解.
【详解】解:∵是的直径,
是的中点,
是的中位线,
故选:B.
6.C
【分析】本题考查相似三角形的判定定理,熟悉掌握判定定理是解决本题的关键.
【详解】解:∵,
∴,
A. 添加,可得到相似,不符合题意;
B. 添加,可得到相似,不符合题意;
C.添加 ,不能得到相似,符合题意;
D. 添加,可得到相似,不符合题意;
故选C.
7.D
【分析】本题考查了位似三角形的性质,相似三角形的判定与性质,熟练掌握位似三角形的性质和相似三角形的判定与性质是解答本题的关键,分别过点,作轴于点,轴于点,证明,结合与关于点位似,得到,从而求得点的横坐标.
【详解】如图,分别过点,作轴于点,轴于点,
,
,
,
与关于点位似,且位似比为,
,
,
,
,
点的横坐标为,
故选:D.
8.B
【分析】本题主要考查了二次函数的图象和性质,根据图象与x轴的交点个数,即可判断①;根据抛物线的对称性可得与x轴的另一交点在点和之间,即可判断②;根据函数的对称轴,即可判断③;将点代入即可判断④.
【详解】解:由图象可得:抛物线与x轴有两个交点,
∴有两个不同的根,
∴,故①错误;
∵抛物线的顶点为,与x轴的交点A在点和之间,
∴与x轴的另一交点在点和之间,
∴时,,故②错误;
∵抛物线的顶点为,
∴,即,故③正确;
当时,,
故④正确;
故选:B.
9.
【分析】本题主要考查了求概率,根据题意画出树状图表示出所有结果,再找出两张卡片正面图案恰好是三角形和菱形的种数,利用即可解题.
【详解】解:根据题意,可画树状图如下:
由图可知,总共有12种结果,其中两张卡片正面图案恰好是三角形和菱形的有2种,所以两张卡片正面图案恰好是三角形和菱形的概率是.
故答案为:.
10.
【分析】本题考查了比例的性质,代数式求值.熟练掌握比例的性质,代数式求值是解题的关键.
由,可得,根据,计算求解即可.
【详解】解:∵,
∴,
∴,
故答案为:.
11.
【分析】本题考查了二次函数的性质;根据条件变形为,确定出a的取值范围,将转化为即可.
【详解】∵,
∴,,
∴,
∵,
∴,
∴,
∴,
∵,
∴当时,式子的值随的增大而增大,
∴当时,的最大值为.
故答案为.
12. 12
【分析】本题主要考查了二次函数与y轴的交点问题,二次函数的对称性等等,抛物线与轴正半轴有交点,则,解得;先求出对称轴为直线,进而由对称性得到当时,抛物线在轴下方,再由当时,抛物线在轴上方,可得当时,,则,解方程即可得到答案.
【详解】解:∵在平面直角坐标系中,抛物线与轴正半轴有交点,
∴,
∴;
∵抛物线解析式为,
∴抛物线对称轴为直线,
∵当时,抛物线在轴下方,
∴当时,抛物线在轴下方,
又∵当时,抛物线在轴上方,
∴当时,,
∴,
∴;
故答案为:;12.
13.或
【分析】本题考查了二次函数与一次函数的交点问题、二次函数与一元二次方程,由图象可知,、图象的交点的横坐标为和,则当或时,,由此即可得到答案,采用数形结合的思想是解此题的关键.
【详解】解:由图象可知,、图象的交点的横坐标为和,
当或时,,
关于的方程的解为或,
故答案为:或.
14.
【分析】作点N关于的对称点,则点在上,连接交于P,此时的值最小,最小值为的长,连接,,,求出,证明是正三角形,可得,然后可得答案.
【详解】解:如图,作点N关于的对称点,则点在上,连接交于P,此时的值最小,最小值为的长,连接,,,
∵N是弧的中点,
∴,
∵,
∴,
∴,
∴,
∵,
∴是正三角形,
∴,
又∵,
∴周长的最小值为,
故答案为:.
【点睛】本题考查了圆周角定理,圆心角、弧、弦的关系,利用轴对称求最短路径,等边三角形的判定和性质,作出辅助线,确定出取最小值时点P的位置是解题的关键.
15.3或/或/或/或
【分析】本题考查了翻折变换(折叠问题),矩形的性质,相似三角形的判定和性质,勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题.
【详解】解:在矩形中,
∵,,
∴,,
∵E是的中点,
∴,
∴,
当时,过点作于H.设,则,,
∵,
∴
又∵,
∴,
∵,
∴,
∴;
当时,
.
综上所述,满足条件的的值为3或.
16.
【分析】本题考查了扇形面积,勾股定理和折叠问题.解题关键是利用参数构建方程解决问题.
连接,由勾股定理求出由折叠可得出,设,则 ,在中,由勾股定理建立关于x方程求解,根据即可求解.
【详解】解:连接,
,,
,
在中,由勾股定理,得
,
由折叠可得,,
,
设则,
则根据勾股定理,
解得,
∴阴影部分的面积是:.
17.(1)
(2)
【分析】本题考查了简单的概率计算,列举法求概率.熟练掌握简单的概率计算,列举法求概率是解题的关键.
(1)利用概率公式计算概率即可;
(2)根据题意列表,然后求概率即可.
【详解】(1)解:由题意知,小明抽到“直隶总督署”志愿服务的概率是,
故答案为:;
(2)解:由题意列表如下:
小亮 小明
共有16种等可能的结果,小明和小亮抽到同一景区志愿服务的结果有4种,
∴(抽到同一景区志愿服务),
∴他们抽到同一景区志愿服务的概率为.
18.(1)①;②或
(2)或
【分析】本题主要考查了二次函数的图象和性质,熟练掌握二次函数的图象和性质,利用二次函数的性质解决问题是解题的关键.
(1)①由点在抛物线上,可得,从而得出,可得抛物线的对称轴为直线;②由抛物线的对称轴为直线,可得,从而得出抛物线顶点坐标为,再由二次函数的性质得出a的取值范围;
(2)由当时,,可得点A在抛物线与x轴围成的图象的内部,再分当时及当时两种情况进行讨论,求出b的取值范围;
【详解】(1)①∵点在抛物线上,
∴,
∴,
∴抛物线的对称轴为直线;
②∵抛物线的对称轴为直线,
∴,
∴抛物线顶点坐标为,
∵点在抛物线上,
∴当时,,解得;
当时,,解得
综上所述,或.
(2)当时,,
∴点A在抛物线与x轴围成的图象的内部,
∵当时,,
当时,点A在第一象限内,
∴点A在抛物线与x轴围成的图象的内部,
∴线段只有和在左侧的抛物线相交,
∵抛物线与线段恰有一个公共点,
∴,
∴或,
∵,
∴,
当时,点A在第一象限内,
∴点A在抛物线与x轴围成的图象的内部,
∴线段只有和在右侧的抛物线相交,
∵抛物线与线段恰有一个公共点,
∴,
∴或,
∵,
∴,
即满足条件的m的范围为或.
19.见解析
【分析】本题主要考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解题的关键.先根据圆内接四边形的性质得出,再根据,圆周角定理证明,即可得出结论.
【详解】证明:四边形内接于,
.
又,
.
,
,
,
,
,即平分.
20.(1)见解析
(2)
【分析】本题考查了三角形相似的判定和性质,勾股定理,直角三角形斜边的中线等于斜边的一半.
(1)根据,C是的中点,得到,,证明即可.
(2)根据相似三角形的性质计算即可.
【详解】(1)∵,C是的中点,
∴,,
∴,,
∴,
∴.
(2)∵,
∴,
∵,
设,则,
根据勾股定理,得,
∴,
∴.
21.
【分析】本题考查了相似三角形的判定和性质,勾股定理,等腰三角形的性质,由等腰三角形的性质可得,,进而证明,得到,由线段的和差和勾股定理得到,,把数据代入比例式即可求解,掌握相似三角形的判定和性质是解题的关键.
【详解】解:如图,连接,与的延长线交于点,
由题意可得,,,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,,,
∴,,
∴,
解得,
∴,
答:两点之间的距离为.
22.(1)1或3
(2)或
(3)
(4)
【分析】本题考查了抛物线与x轴的交点:把求二次函数(a,b,c是常数,)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质.
(1)看二次函数与x轴交点的横坐标即可;
(2)看x轴下方的二次函数的图象相对应的x的范围即可;
(3)在对称轴的右侧即为y随x的增大而减小;
(4)得到相对应的函数看是怎么平移得到的即可.
【详解】(1)解:∵二次函数的图象与x轴的交点为,,
∴方程的两个根为;
(2)∵由图象可知或时,二次函数的图象在x轴下方,
∴不等式的解集为或;
(3)∵抛物线的对称轴为直线,开口向下,
∴当y随x的增大而减小时,自变量x的取值范围是;
(4)∵由图象可知二次函数图象的顶点坐标为,
当直线在的下方时,一定与抛物线有两个不同的交点,
∴当时,方程有两个不相等的实数根.
23.(1)见解析
(2)见解析
(3)
【分析】(1)连接、,,根据同弧或等弧所对的圆周角相等,圆心角是圆周角的2倍,推导出,,,,得到,即可证明;
(2)连接,在上截取,延长交圆于点N,连接,可得是等腰三角形,再由弧的关系得到,则,得到,即可证明;
(3)连接,作的平分线交于点K,过K点作交于点L,根据弧的关系得到,设,则,在中,,解得,分别可求,在中,,解得,,求出,再由A、F、D、C四点共圆,推导出,得到,求出,圆O的半径为.
【详解】(1)证明:连接、,,
∵,
∴,
∵,
∴,
∴,
∵C是的中点,
∴,
∴
,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴;
(2)证明:连接,在上截取,延长交圆于点N,连接,
∵,,
∴是等腰三角形,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴;
(3)解:连接,作的平分线交于点K,过K点作交于点L,
∵是圆的直径,
∴,
∵,,
∴,
∴,
∴,
设,则,
∵,
∴,
∵,
在中,,
解得,
∴,
∵,,,
∴,
∴,
在中,,
解得,
∴,
∴,
∵A、F、D、C四点共圆,
∴,
∴,
∴,
∴,
∴,
∴圆O的半径为.
【点睛】本题考查圆的综合应用,熟练掌握圆周角与圆心角定理,四点共圆的性质,等腰三角形的性质,垂径定理是解题的关键.
24.(1)①;②
(2)在,见解析
(3)当时,;当时,;当,
【分析】(1)①求出点B的坐标,代入二次函数解析式求出b的值即可;②根据①的解析式求出A点坐标,再根据图象得出结论;
(2)由抛物线解析式求出顶点坐标,将顶点坐标代入直线解析式求解;
(3)根据抛物线的顶点在的内部,确定b的取值范围,由于抛物线的对称轴为,再根据点,点的横坐标与对称轴的距离和抛物线的增减性进行判断.
【详解】(1)解:①直线分别交y轴于点B,
当时,,
因此,
把点代入二次函数关系式得:,
解得:
∴二次函数解析式为;
②由①知,二次函数解析式为,
当时,,
解得
,
由图象,得当时,
x的取值范围是;
(2)点M在直线上,理由:
∵点M为二次函数图象的顶点,
∴M的坐标是,
把代入,
得,
故答案为:点M在直线上;
(3)
二次函数图象的顶点在内部,
,
解得:,
由抛物线的对称轴为,
①当时,点,根据抛物线的对称性和增减性可得:,
②当时,点,根据抛物线的对称性和增减性可得: ,
③当时,点,根据抛物线的对称性和增减性可得:,
故答案为:当时,;当时,;当时,.
【点睛】本题考查二次函数与不等式(组)之间的关系、二次函数的性质,解题关键是掌握二次函数与方程及不等式的关系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末易错点检测卷-2023-2024学年数学九年级上册浙教版
一、单选题
1.下列事件中,是必然事件的是( )
A.从一副扑克牌中到红桃 B.打开电视,正在播放新闻
C.两个无理数的积是无理 D.三角形的内角和为
2.下列关于二次函数的图象和性质的说法中,正确的是( )
A.图象开口向上 B.对称轴是直线
C.顶点坐标是 D.在此函数图象上
3.下列函数中,当时,随的增大而减小的是( )
A. B. C. D.
4.如图,将一个含角的直角三角板绕点A顺时针旋转,点C的对应点为点,若点落在延长线上,则旋转角的度数是( )
A. B. C. D.
5.如图,是的弦,是的直径,已知,,连接,若D是的中点,则的长( )
A. B. C. D.
6.如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
7.已知:如图与关于点位似,且位似比为,设的横坐标为,则的对应点的横坐标为( )
A. B. C. D.
8.如图所示,抛物线的顶点为,与x轴的交点A在点和之间,以下结论:①;②;③;④,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.现有四张卡片,正面图案如图所示,它们除此之外完全相同,把这四张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面图案恰好是三角形和菱形的概率是 .
10.若,则 .
11.实数,满足,则的最大值为 .
12.在平面直角坐标系中,抛物线与轴正半轴有交点,则的取值范围 ,当时,抛物线在轴上方;当时,抛物线在轴下方,则 .
13.如图,二次函数与一次函数的图象相交于两点,则关于的方程的解为 .
14.如图,是的直径,,点M在上,,N是弧的中点,P是直径上的一动点.若,则周长的最小值为 .
15.如图,在矩形中,,,是的中点,连接,P是边上一动点,过点P的直线将矩形折叠,使点D落在上的处,当是以为腰的等腰三角形时,
16.如图,扇形中,,,点C为上一点,将扇形沿折叠,使点B的对应点落在射线上,则图中阴影部分的面积为 .
三、解答题
17.“这么近,那么美,周末到河北.”越来越多的外地游客利用假期来领略河北优美的自然风光和厚重的历史文化.保定市莲池区某中学组建了一支学生讲解员队伍,到下面四个景区志愿服务.
景区有:直隶总督署—用A表示;古莲花池—用B表示;淮军公所—用C表示;保定军校博物馆—用D表示,
将编号A,B,C,D分别写在四张卡片上,每名同学随机抽取一张后放回,并到其抽到的景区志愿服务.
(1)小明抽到“直隶总督署”志愿服务的概率是__________.
(2)小明和小亮是同班同学,求他们抽到同一景区志愿服务的概率.(请用树状图或列表的方法写出分析过程)
18.在平面直角坐标系中,有抛物线.
(1)若点在抛物线上,
①求抛物线的对称轴;
②若点也在抛物线上,求a的取值范围;
(2)当时,有已知点,若抛物线与线段只有一个公共点,结合函数图象,求b的取值范围.
19.如图,四边形内接于,E为延长线上一点,连接,若.求证:平分.
20.如图,,C是的中点.
(1)求证:;
(2)当时,求的值.
21.如图是文件夹在常态下的侧面示意图.已知文件夹是轴对称图形, ,点 在对称轴上,于点.若,,,求两点之间的距离.
22.二次函数的图象如图所示,根据图象解答下列问题.
(1)写出方程的两个根
(2)写出不等式的解集
(3)写出随的增大而减小的自变量的取值范围.
(4)若方程有两个不相等的实数根,直接写出的取值范围.
23.已知,在中,弦、相交于E,点C是的中点.
(1)如图1,当是直径时,求证:;
(2)如图2,当时,求证:;
(3)如图3,在(2)的条件下,连接,作直径,连接并延长交的延长线于G,,,求的半径长.
24.已知点M为二次函数图象的顶点,直线与轴、轴交于两点.
(1)如图1,若二次函数的图象也过点,
①求抛物线的解析式;
②若,根据图象直接写出x的范围;
(2)判断顶点M是否在直线上,并说明理由;
(3)如图2,点A的坐标为点M在内,若点都在二次函数图象上,试比较与的大小.
参考答案:
1.D
【分析】本题考查了必然事件和随机事件的定义,无理数的乘积,三角形内角和定理,理解“对于一个事件,有可能发生也有可能不发生,这个事件叫做随机事件;对于一个事件,一定会发生,这个事件叫做必然事件.”是解题的关键.
【详解】解:A.从一副扑克牌中到红桃是随机事件,不符合题意;
B.打开电视,正在播放新闻是随机事件,不符合题意;
C.两个无理数的积是无理是随机事件,不符合题意;
D.三角形的内角和为是必然事件,故符合题意;
故选:D.
2.D
【分析】本题考查了二次函数的图象与性质,熟练掌握二次函数的图象与性质是解答本题的关键.
根据二次函数的图象与性质对每一个选项进行分析,只有选项符合题意.
【详解】解:根据题意得:
、,图像开口向下,本选项说法不正确,故不符合题意;
、,对称轴是直线,本选项说法不正确,故不符合题意;
、,,顶点坐标为,本选项说法不正确,故不符合题意;
、当时,,在此函数图象上,本选项说法正确,故符合题意.
故选:.
3.B
【分析】本题主要考查反比例函数、二次函数、正比例函数图像的性质,根据各函数的解析式,逐项分析判断,即可求解.
【详解】解:A、正比例函数的图像,随的增大而增大,
故此选项不符合题意;
B、反比例函数的图像,当时,随的增大而减小,
故此选项符合题意;
C、二次函数的图像,开口向上,对称轴为轴,
当时,y随x的增大而增大,故此选项不符合题意;
D、反比例函数的图像,,当时,随的增大而增大,故此选项不符合题意;
故选:B.
4.D
【分析】本题主要考查旋转的性质,根据旋转角的定义,两对应边的夹角就是旋转角,即可求解.
【详解】解:∵将一个含角的直角三角板绕点A逆时针旋转,点C的对应点为点,若点落在BA延长线上,
∴旋转角是.
故选:D.
5.B
【分析】本题考查圆周角定理,含角的直角三角形的性质,三角形的中位线定理,证明为的中位线是解题的关键,属于中考常考题型.
由直径所对的圆周角是直角得,根据含角的直角三角形的性质得,证明是的中位线,由三角形的中位线定理即可求解.
【详解】解:∵是的直径,
是的中点,
是的中位线,
故选:B.
6.C
【分析】本题考查相似三角形的判定定理,熟悉掌握判定定理是解决本题的关键.
【详解】解:∵,
∴,
A. 添加,可得到相似,不符合题意;
B. 添加,可得到相似,不符合题意;
C.添加 ,不能得到相似,符合题意;
D. 添加,可得到相似,不符合题意;
故选C.
7.D
【分析】本题考查了位似三角形的性质,相似三角形的判定与性质,熟练掌握位似三角形的性质和相似三角形的判定与性质是解答本题的关键,分别过点,作轴于点,轴于点,证明,结合与关于点位似,得到,从而求得点的横坐标.
【详解】如图,分别过点,作轴于点,轴于点,
,
,
,
与关于点位似,且位似比为,
,
,
,
,
点的横坐标为,
故选:D.
8.B
【分析】本题主要考查了二次函数的图象和性质,根据图象与x轴的交点个数,即可判断①;根据抛物线的对称性可得与x轴的另一交点在点和之间,即可判断②;根据函数的对称轴,即可判断③;将点代入即可判断④.
【详解】解:由图象可得:抛物线与x轴有两个交点,
∴有两个不同的根,
∴,故①错误;
∵抛物线的顶点为,与x轴的交点A在点和之间,
∴与x轴的另一交点在点和之间,
∴时,,故②错误;
∵抛物线的顶点为,
∴,即,故③正确;
当时,,
故④正确;
故选:B.
9.
【分析】本题主要考查了求概率,根据题意画出树状图表示出所有结果,再找出两张卡片正面图案恰好是三角形和菱形的种数,利用即可解题.
【详解】解:根据题意,可画树状图如下:
由图可知,总共有12种结果,其中两张卡片正面图案恰好是三角形和菱形的有2种,所以两张卡片正面图案恰好是三角形和菱形的概率是.
故答案为:.
10.
【分析】本题考查了比例的性质,代数式求值.熟练掌握比例的性质,代数式求值是解题的关键.
由,可得,根据,计算求解即可.
【详解】解:∵,
∴,
∴,
故答案为:.
11.
【分析】本题考查了二次函数的性质;根据条件变形为,确定出a的取值范围,将转化为即可.
【详解】∵,
∴,,
∴,
∵,
∴,
∴,
∴,
∵,
∴当时,式子的值随的增大而增大,
∴当时,的最大值为.
故答案为.
12. 12
【分析】本题主要考查了二次函数与y轴的交点问题,二次函数的对称性等等,抛物线与轴正半轴有交点,则,解得;先求出对称轴为直线,进而由对称性得到当时,抛物线在轴下方,再由当时,抛物线在轴上方,可得当时,,则,解方程即可得到答案.
【详解】解:∵在平面直角坐标系中,抛物线与轴正半轴有交点,
∴,
∴;
∵抛物线解析式为,
∴抛物线对称轴为直线,
∵当时,抛物线在轴下方,
∴当时,抛物线在轴下方,
又∵当时,抛物线在轴上方,
∴当时,,
∴,
∴;
故答案为:;12.
13.或
【分析】本题考查了二次函数与一次函数的交点问题、二次函数与一元二次方程,由图象可知,、图象的交点的横坐标为和,则当或时,,由此即可得到答案,采用数形结合的思想是解此题的关键.
【详解】解:由图象可知,、图象的交点的横坐标为和,
当或时,,
关于的方程的解为或,
故答案为:或.
14.
【分析】作点N关于的对称点,则点在上,连接交于P,此时的值最小,最小值为的长,连接,,,求出,证明是正三角形,可得,然后可得答案.
【详解】解:如图,作点N关于的对称点,则点在上,连接交于P,此时的值最小,最小值为的长,连接,,,
∵N是弧的中点,
∴,
∵,
∴,
∴,
∴,
∵,
∴是正三角形,
∴,
又∵,
∴周长的最小值为,
故答案为:.
【点睛】本题考查了圆周角定理,圆心角、弧、弦的关系,利用轴对称求最短路径,等边三角形的判定和性质,作出辅助线,确定出取最小值时点P的位置是解题的关键.
15.3或/或/或/或
【分析】本题考查了翻折变换(折叠问题),矩形的性质,相似三角形的判定和性质,勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题.
【详解】解:在矩形中,
∵,,
∴,,
∵E是的中点,
∴,
∴,
当时,过点作于H.设,则,,
∵,
∴
又∵,
∴,
∵,
∴,
∴;
当时,
.
综上所述,满足条件的的值为3或.
16.
【分析】本题考查了扇形面积,勾股定理和折叠问题.解题关键是利用参数构建方程解决问题.
连接,由勾股定理求出由折叠可得出,设,则 ,在中,由勾股定理建立关于x方程求解,根据即可求解.
【详解】解:连接,
,,
,
在中,由勾股定理,得
,
由折叠可得,,
,
设则,
则根据勾股定理,
解得,
∴阴影部分的面积是:.
17.(1)
(2)
【分析】本题考查了简单的概率计算,列举法求概率.熟练掌握简单的概率计算,列举法求概率是解题的关键.
(1)利用概率公式计算概率即可;
(2)根据题意列表,然后求概率即可.
【详解】(1)解:由题意知,小明抽到“直隶总督署”志愿服务的概率是,
故答案为:;
(2)解:由题意列表如下:
小亮 小明
共有16种等可能的结果,小明和小亮抽到同一景区志愿服务的结果有4种,
∴(抽到同一景区志愿服务),
∴他们抽到同一景区志愿服务的概率为.
18.(1)①;②或
(2)或
【分析】本题主要考查了二次函数的图象和性质,熟练掌握二次函数的图象和性质,利用二次函数的性质解决问题是解题的关键.
(1)①由点在抛物线上,可得,从而得出,可得抛物线的对称轴为直线;②由抛物线的对称轴为直线,可得,从而得出抛物线顶点坐标为,再由二次函数的性质得出a的取值范围;
(2)由当时,,可得点A在抛物线与x轴围成的图象的内部,再分当时及当时两种情况进行讨论,求出b的取值范围;
【详解】(1)①∵点在抛物线上,
∴,
∴,
∴抛物线的对称轴为直线;
②∵抛物线的对称轴为直线,
∴,
∴抛物线顶点坐标为,
∵点在抛物线上,
∴当时,,解得;
当时,,解得
综上所述,或.
(2)当时,,
∴点A在抛物线与x轴围成的图象的内部,
∵当时,,
当时,点A在第一象限内,
∴点A在抛物线与x轴围成的图象的内部,
∴线段只有和在左侧的抛物线相交,
∵抛物线与线段恰有一个公共点,
∴,
∴或,
∵,
∴,
当时,点A在第一象限内,
∴点A在抛物线与x轴围成的图象的内部,
∴线段只有和在右侧的抛物线相交,
∵抛物线与线段恰有一个公共点,
∴,
∴或,
∵,
∴,
即满足条件的m的范围为或.
19.见解析
【分析】本题主要考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解题的关键.先根据圆内接四边形的性质得出,再根据,圆周角定理证明,即可得出结论.
【详解】证明:四边形内接于,
.
又,
.
,
,
,
,
,即平分.
20.(1)见解析
(2)
【分析】本题考查了三角形相似的判定和性质,勾股定理,直角三角形斜边的中线等于斜边的一半.
(1)根据,C是的中点,得到,,证明即可.
(2)根据相似三角形的性质计算即可.
【详解】(1)∵,C是的中点,
∴,,
∴,,
∴,
∴.
(2)∵,
∴,
∵,
设,则,
根据勾股定理,得,
∴,
∴.
21.
【分析】本题考查了相似三角形的判定和性质,勾股定理,等腰三角形的性质,由等腰三角形的性质可得,,进而证明,得到,由线段的和差和勾股定理得到,,把数据代入比例式即可求解,掌握相似三角形的判定和性质是解题的关键.
【详解】解:如图,连接,与的延长线交于点,
由题意可得,,,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,,,
∴,,
∴,
解得,
∴,
答:两点之间的距离为.
22.(1)1或3
(2)或
(3)
(4)
【分析】本题考查了抛物线与x轴的交点:把求二次函数(a,b,c是常数,)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质.
(1)看二次函数与x轴交点的横坐标即可;
(2)看x轴下方的二次函数的图象相对应的x的范围即可;
(3)在对称轴的右侧即为y随x的增大而减小;
(4)得到相对应的函数看是怎么平移得到的即可.
【详解】(1)解:∵二次函数的图象与x轴的交点为,,
∴方程的两个根为;
(2)∵由图象可知或时,二次函数的图象在x轴下方,
∴不等式的解集为或;
(3)∵抛物线的对称轴为直线,开口向下,
∴当y随x的增大而减小时,自变量x的取值范围是;
(4)∵由图象可知二次函数图象的顶点坐标为,
当直线在的下方时,一定与抛物线有两个不同的交点,
∴当时,方程有两个不相等的实数根.
23.(1)见解析
(2)见解析
(3)
【分析】(1)连接、,,根据同弧或等弧所对的圆周角相等,圆心角是圆周角的2倍,推导出,,,,得到,即可证明;
(2)连接,在上截取,延长交圆于点N,连接,可得是等腰三角形,再由弧的关系得到,则,得到,即可证明;
(3)连接,作的平分线交于点K,过K点作交于点L,根据弧的关系得到,设,则,在中,,解得,分别可求,在中,,解得,,求出,再由A、F、D、C四点共圆,推导出,得到,求出,圆O的半径为.
【详解】(1)证明:连接、,,
∵,
∴,
∵,
∴,
∴,
∵C是的中点,
∴,
∴
,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴;
(2)证明:连接,在上截取,延长交圆于点N,连接,
∵,,
∴是等腰三角形,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴;
(3)解:连接,作的平分线交于点K,过K点作交于点L,
∵是圆的直径,
∴,
∵,,
∴,
∴,
∴,
设,则,
∵,
∴,
∵,
在中,,
解得,
∴,
∵,,,
∴,
∴,
在中,,
解得,
∴,
∴,
∵A、F、D、C四点共圆,
∴,
∴,
∴,
∴,
∴,
∴圆O的半径为.
【点睛】本题考查圆的综合应用,熟练掌握圆周角与圆心角定理,四点共圆的性质,等腰三角形的性质,垂径定理是解题的关键.
24.(1)①;②
(2)在,见解析
(3)当时,;当时,;当,
【分析】(1)①求出点B的坐标,代入二次函数解析式求出b的值即可;②根据①的解析式求出A点坐标,再根据图象得出结论;
(2)由抛物线解析式求出顶点坐标,将顶点坐标代入直线解析式求解;
(3)根据抛物线的顶点在的内部,确定b的取值范围,由于抛物线的对称轴为,再根据点,点的横坐标与对称轴的距离和抛物线的增减性进行判断.
【详解】(1)解:①直线分别交y轴于点B,
当时,,
因此,
把点代入二次函数关系式得:,
解得:
∴二次函数解析式为;
②由①知,二次函数解析式为,
当时,,
解得
,
由图象,得当时,
x的取值范围是;
(2)点M在直线上,理由:
∵点M为二次函数图象的顶点,
∴M的坐标是,
把代入,
得,
故答案为:点M在直线上;
(3)
二次函数图象的顶点在内部,
,
解得:,
由抛物线的对称轴为,
①当时,点,根据抛物线的对称性和增减性可得:,
②当时,点,根据抛物线的对称性和增减性可得: ,
③当时,点,根据抛物线的对称性和增减性可得:,
故答案为:当时,;当时,;当时,.
【点睛】本题考查二次函数与不等式(组)之间的关系、二次函数的性质,解题关键是掌握二次函数与方程及不等式的关系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
