期末易错精选题-2023-2024学年数学九年级上册苏科版(含解析)
文档属性
| 名称 | 期末易错精选题-2023-2024学年数学九年级上册苏科版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 06:56:24 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末易错精选题-2023-2024学年数学九年级上册苏科版
一、单选题
1.下列方程是一元二次方程的是( )
A. B. C. D.
2.某学校开设了劳动教育课程,小康从感兴趣的“手工”“种植”“烹饪”“陶艺”“木工”5门课程中随机选择一门课程学习,假设每门课程被选中的可能性相等,则小康恰好选中“陶艺”的概率为( )
A. B. C. D.
3.已知关于x的一元二次方程的一个根为,则m的值为( )
A.-2 B.0 C.2 D.4
4.某农家前年水蜜桃亩产量为800千克,今年的亩产量为1250千克,设从前年到今年的年平均增长率为x,则可列方程( )
A. B.
C. D.
5.习近平总书记指出:“扶贫先扶志,扶贫必扶智”,某企业扶贫小组准备为贫困户送温暖活动,该企业对扶贫对象的年龄结构进行了随机抽样调查,调查所得的一组数据的方差公式是,则这组数据的平均数和样本容量分别是( )
A.50,45 B.50,28 C.45,50 D.45,36
6.如图,是的直径,,是上的两点,若,则的大小为( )
A. B. C. D.
7.如图,在扇形中,,点为弦上一动点(不与两点重合),连接并延长交于点,当为最大值时,的长为( )
A. B. C. D.
8.如图,的内切圆分别与,,相切于点D,E,F,且,,则的周长为( )
A.16 B.14 C.12 D.10
二、填空题
9.一元二次方程化成一般形式后的常数项是 .
10.一组数据有个数,它们的平方和是,平均数是,则这组数据的方差是 .
11.在直角坐标系中,的圆心P的坐标为,半径为2,当与直线相切时m的值为 .
12.平面内有5个点A,B,C,D,E,直线与直线正好相交于点E,在这5个点中,过其中3个点能确定一个圆的概率是 .
13.小涵同学家开了一家超市,9月份盈利元,月份盈利达到元,每月盈利的平均增长率都相同,设每月盈利的平均增长率为x,则可列方程为 .
14.如图,是的直径,是上一点,若,则 .
15.如图,P为外一点,与相切于点A,交于点B,交于点C,,,则的半径为 .
16.杭州亚运会开幕式出现一座古今交汇拱底桥,桥面呈拱形.该桥的中间拱洞可以看成一种特殊的圆拱桥,此圆拱桥的跨径(桥拱圆弧所对的弦的长)约为,拱高(桥拱圆弧的中点到弦的距离)约为,则此桥拱的半径是 .
三、解答题
17.解方程:
(1)
(2)
18.小明和小亮用如图所示的同一个转盘进行“配紫色”游戏.游戏规则如下:连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色),则小明得1分,否则小亮得1分.你认为这个游戏对双方公平吗?请说明理由.若不公平,请你修改规则使游戏对双方公平.
19.已知关于的一元二次方程.
(1)求证:对于任意实数,该方程总有实数根;
(2)若这个一元二次方程的一根大于2,求的取值范围.
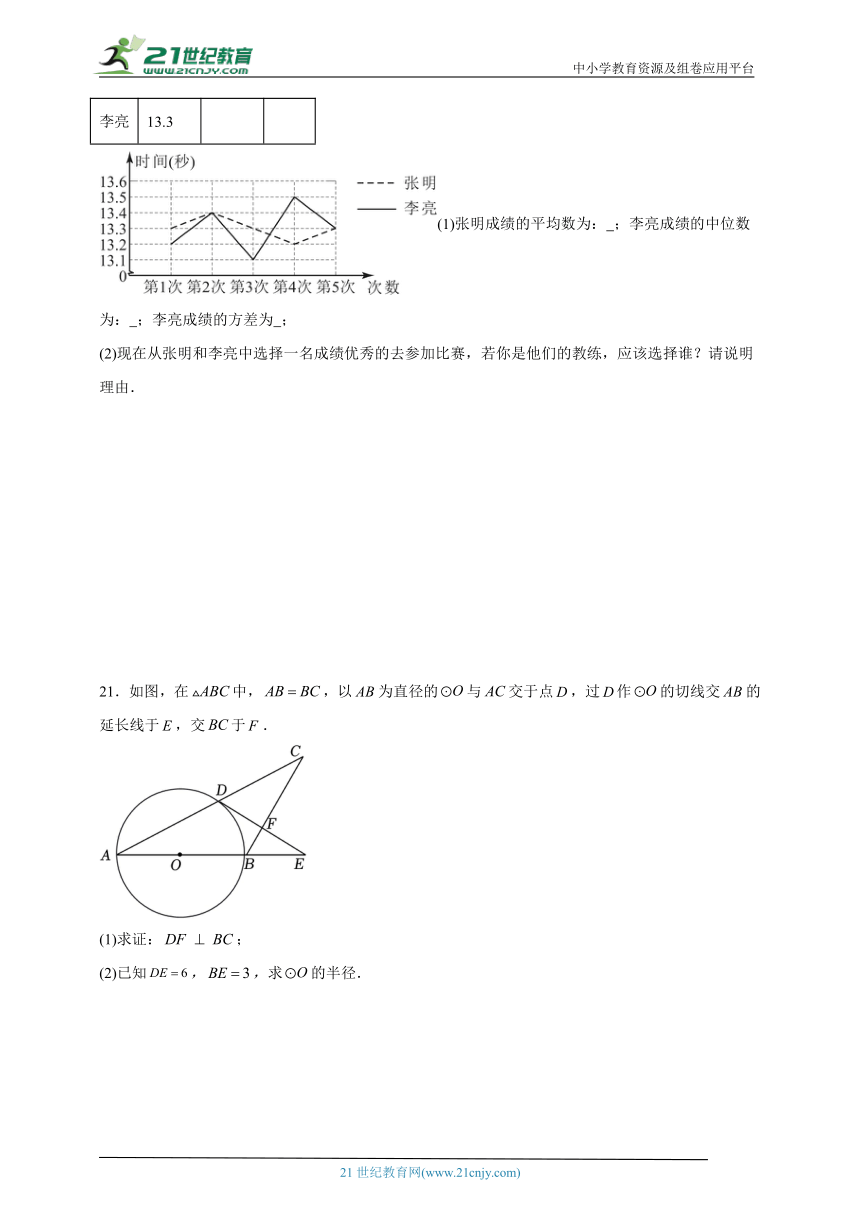
20.学校为了让同学们走向操场、积极参加体育锻炼,启动了“学生阳光体育运动”,张明和李亮在体育运动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
平均数 中位数 方差
张明 13.3 0.004
李亮 13.3
(1)张明成绩的平均数为: ;李亮成绩的中位数为: ;李亮成绩的方差为 ;
(2)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.
21.如图,在中,,以为直径的与交于点,过作的切线交的延长线于,交于.
(1)求证:;
(2)已知,,求的半径.
22.如1图是一款利用曲边三角形制造的扫地机. 如2 图是一个曲边三角形,它可按照如下方法作出:作等边三角形,分别以点A,B,C为圆心, 以的长为半径作,,,三段弧所围成的图形就是曲边三角形. 若这个曲边三角形的周长为,求它的面积(结果保留π).
23.如图,已知弓形的弦长,弓高,(,并经过圆心).
(1)请利用尺规作图的方法找到圆心;(保留作图痕迹,不必写作法)
(2)求弓形所在的半径的长.
参考答案:
1.C
【分析】根据一元二次方程的定义逐项判断即可得出答案.
【详解】解:中含有两个未知数,因此不是一元二次方程,故A选项不合题意;
不是整式方程,因此不是一元二次方程,故B选项不合题意;
中只含有一个未知数,未知数的最高次数是2,并且是整式方程,因此是一元二次方程,故C选项符合题意;
中含有两个未知数,因此不是一元二次方程,故D选项不合题意;
故选C.
【点睛】本题考查一元二次方程的识别,解题的关键是掌握定义,即通过化简后,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的整式方程,叫做一元二次方程.
2.B
【分析】本题考查了简单的概率计算.熟练掌握概率公式计算概率是解题的关键.
根据概率公式计算求解即可.
【详解】解:由题意知,小康恰好选中“陶艺”的概率为,
故选:B.
3.C
【分析】本题主要考查解一元二次方程的根,将代入方程即可求解,掌握解一元二次方程的根的计算方法是解题的关键.
【详解】解:根据题意,将代入方程得,
,
解得,,
故选:.
4.D
【分析】本题考查由实际问题抽象出一元二次方程的知识,可先表示出去年水蜜桃的亩产量,那么去年水蜜桃的亩产量,把相应数值代入即可求解.
【详解】解:去年水蜜桃的亩产量为,今年水蜜桃的亩产量在去年水蜜桃的亩产量的基础上增加x,为,
则列出的方程是,
故选:D.
5.C
【分析】本题主要考查平均数和样本容量的定义及方差,熟练掌握平均数和样本容量的定义及方差是解题的关键.
根据平均数的概念和样本容量指的是一个样本中所包含的单位数及方差公式的意义可直接进行求解.
【详解】解:∵一组数据的方差公式是
∴这组数据的平均数为45,样本容量为50.
故选C.
6.C
【分析】根据直径对的圆周角为直角得到,再根据同圆中同弧对的圆周角相等得到,即可求出.
此题主要考查了圆周角定理.熟练掌握直径所对的圆周角是直角,同圆中同弧所对的圆周角相等,是解决问题的关键.
【详解】∵为⊙O的直径,
∴,
∵,
∴.
故选:C.
7.B
【分析】本题考查的是垂线段最短的应用,垂径定理的应用,求解弧长,先过作交于,交弧于,可得此时最短,则最长,即为的位置,为的位置,再结合垂径定理与弧长公式可得答案.
【详解】解:如图,过作交于,交弧于,
此时最短,则最长,即为的位置,为的位置,
∴,,
∵,
∴的长度为:,
即的长度为:;
故选B
8.A
【分析】本题考查切线长定理,熟练掌握切线长定理是解题的关键.根据切线长定理得到,,,根据即可得到的周长.
【详解】解:∵的内切圆分别与,,相切于点D,E,F,且,
∴,,,
∵,
∴,
∴的周长,
故选:A.
9.
【分析】本题考查了一元二次方程的一般形式;
移项后将一元二次方程化为一般形式,然后可得答案.
【详解】解:将方程化为一般形式为,
其常数项为.
故答案为:.
10.
【分析】此题主要考查了方差的求法,解决问题的关键是对方差公式的正确应用.根据已知条件个数据的平方和是,平均数是,可知应该应用求方差公式推导出代入求出即可.
【详解】解:根据求方差公式:
,
故答案为:.
11.或
【分析】本题主要考查坐标与图形,切线的性质,一次函数图象与性质等知识,作轴于点E,交直线于点F,切点为点G,直线与y轴交点为Q,求得,证明,,由勾股定理得从而可求出点P在第三象限内的坐标,根据对称性可求出点P在第四象限的坐标.
【详解】解:如图,当点P在第三象限时,
对于,当时,则
作轴于点E,交直线于点F,则
解得,
∴,
∵与相切,
∴
又
∴,
∴
在中,由勾股定理得,,
∴点P的坐标为
∴;
同理可得,点P在第四象限内点的坐标为
∴,
综上,m的值为或
故答案为:或.
12.
【分析】此题考查确定圆的条件:经过不在同一条直线上的三个点确定一个圆;概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种可能,那么事件A的概率.
首先求出五个点任意选取3个点有10种情况,然后根据不在同一条直线上的三个点确定一个圆,所以过其中3个点能确定一个圆的情况有8种,由此求出概率.
【详解】解答:解:平面内有五个点A、B、C、D、E,任选3点有10种情况::A、E、B;A、E、C;A、E、D;A、B、C;A、B、D;C、D、E;B、E、C;B、E、D;A、D、C;B、D、C,
在这五个点中,过其中3个点能确定一个圆的情况是:A、E、C;A、E、D;A、B、C;A、B、D;B、E、C;B、E、D;A、D、C;B、D、C,共8种;
∴概率为:.
故答案为:.
13.
【分析】本题考查了一元二次方程的应用.根据题意正确的列方程是解题的关键.
由题意知,月份盈利,月份盈利,依题意可列方程,然后作答即可.
【详解】解:依题意得,,
故答案为:.
14.
【分析】本题考查圆周角定理,根据“同弧所对的圆周角是圆心角的一半”直接求解即可得到答案,熟记圆周角定理是解决问题的关键.
【详解】解:,
,
故答案为:.
15.6
【分析】本题主要考查了切线的性质得性质与判定,切线长定理,勾股定理,连接,先证明是的切线,进而由切线长定理得到,再由切线的性质得到,利用勾股定理求出,则,设的半径为r,则,在中,由勾股定理得,解方程即可得到答案.
【详解】解:如图所示,连接,
∵,是的半径,
∴是的切线,
∵与相切于点A,
∴,,
在中,由勾股定理得,
∴,
设的半径为r,则,
在中,由勾股定理得,
∴,
解得,
∴的半径为6,
故答案为:6.
16.
【分析】本题主要考查了垂径定理、勾股定理及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.设圆心为,作于点的延长线交圆弧为点,设半径为,根据垂径定理得,,由勾股定理得∶,即可求出答案.
【详解】解:如图,设圆心为,作于点的延长线交圆弧为点,则为优弧的中点,设半径为,
由勾股定理得∶,
解得∶,
故答案为:.
17.(1)
(2)
【分析】本题考查求解一元二次方程.掌握各类求解方法是解题关键.
(1)利用因式分解法即可求解;
(2)利用配方法即可求解.
【详解】(1)解:
,
,;
(2)解:
,
18.游戏不公平,如若两次转出颜色相同或配成紫色.则小明得4分.否则小亮得5分
【分析】本题考查的是概率,熟记概率等于所求情况数与总情况数之比是解题关键.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平﹒游戏是否公平,关键要看是否游戏双方赢的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
【详解】列表如下:
第一次 第二次 红 黄 蓝
红 (红,红) (红,黄) (红,蓝)
黄 (黄,红) (黄,黄) (黄.蓝)
蓝 (蓝,红) (蓝.黄) (蓝,蓝)
由表知,P(小明获胜),P(小亮获胜).
小明的得分为;小亮的得分为.
,
∴游戏不公平.如若两次转出颜色相同或配成紫色.则小明得4分.否则小亮得5分.
19.(1)见解析;
(2).
【分析】本题考查了根的判别式及解一元二次方程,正确运用判别式是解题的关键:
(1)根据一元二次方程判别式为,即可解答;
(2)解方程,求得,,根据题意得到,解不等式即可.
【详解】(1)证明:∵关于x的一元二次方程,
∴,
∴对于任意实数m,该方程总有实数根;
(2)解:设方程的两个实数根为,,
,
∴,,
∵这个一元二次方程的一根大于2,
∴,
解得:,
∴m的取值范围.
20.(1)13.3,13.3,0.02
(2)选择张明参加比赛,理由见解析
【分析】本题考查了平均数,中位数,方差的意义:
(1)利用平均数的计算公式可得出张明成绩的平均数;先将李亮的成绩按照从小到大排列,然后即可得到这组数据的中位数;
(2)在平均数、中位数相同的情况下,再根据方差越小数据越稳定,即可得出答案.
【详解】(1)解:张明成绩的平均数为:(秒);
李亮的成绩是:13.2,13.4,13.1,13.5,13.3,
把这些数从小到大排列为:13.1,13.2,13.3,13.4,13.5,
则李亮成绩的中位数是:13.3秒;
李亮的方差为:
故答案为:13.3,13.3,0.02;
(2)解: 选择张明参加比赛,理由如下:
因为张明和李亮成绩的平均数、中位数都相同,但张明成绩的方差小于李亮成绩的方差,张明成绩比李亮成绩稳定.
21.(1)见解析
(2)
【分析】本题考查的是切线的性质、勾股定理的应用,掌握圆的切线垂直于经过切点的半径是解题的关键.
(1)连接,根据切线的性质可得,再由,,可得,从而得到,即可;
(2)设的半径为r,在中,根据勾股定理,即可求解.
【详解】(1)证明:如图,连接,
∵是的切线,
∴,即,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
(2)设的半径为r,则,
∵,
∴,
在中,,,
∴,
解得:,
即的半径为.
22.
【分析】本题考查扇形面积的计算、等边三角形的性质、弧长的计算,根据题意和图形,可以计算出的长,然后根据扇形面积公式和三角形的面积,可以求得曲边三角形的面积.
【详解】解:由题意可得,
,,
∴,
解得,,
∵是等边三角形,
∵,
作交于点D,
∴,
∴,
∴,
∴一个曲边三角形的面积是:.
23.(1)详见解析
(2)10
【分析】本题考查作图-复杂作图,垂径定理,解直角三角形等知识,解题的关键是理解题意,学会利用参数构建方程解决问题,属于中考常考题型.
(1)作线段的垂直平分线交直线于点O,点O即为所求.
(2)连接,利用垂径定理和勾股定理即可求出.
【详解】(1)解:如图所示,作线段的垂直平分线交直线于点O,点即是圆心;
(2)连接,
,并经过圆心,,
,在中,由勾股定理得:
解得,,
答:的半径的长为10.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末易错精选题-2023-2024学年数学九年级上册苏科版
一、单选题
1.下列方程是一元二次方程的是( )
A. B. C. D.
2.某学校开设了劳动教育课程,小康从感兴趣的“手工”“种植”“烹饪”“陶艺”“木工”5门课程中随机选择一门课程学习,假设每门课程被选中的可能性相等,则小康恰好选中“陶艺”的概率为( )
A. B. C. D.
3.已知关于x的一元二次方程的一个根为,则m的值为( )
A.-2 B.0 C.2 D.4
4.某农家前年水蜜桃亩产量为800千克,今年的亩产量为1250千克,设从前年到今年的年平均增长率为x,则可列方程( )
A. B.
C. D.
5.习近平总书记指出:“扶贫先扶志,扶贫必扶智”,某企业扶贫小组准备为贫困户送温暖活动,该企业对扶贫对象的年龄结构进行了随机抽样调查,调查所得的一组数据的方差公式是,则这组数据的平均数和样本容量分别是( )
A.50,45 B.50,28 C.45,50 D.45,36
6.如图,是的直径,,是上的两点,若,则的大小为( )
A. B. C. D.
7.如图,在扇形中,,点为弦上一动点(不与两点重合),连接并延长交于点,当为最大值时,的长为( )
A. B. C. D.
8.如图,的内切圆分别与,,相切于点D,E,F,且,,则的周长为( )
A.16 B.14 C.12 D.10
二、填空题
9.一元二次方程化成一般形式后的常数项是 .
10.一组数据有个数,它们的平方和是,平均数是,则这组数据的方差是 .
11.在直角坐标系中,的圆心P的坐标为,半径为2,当与直线相切时m的值为 .
12.平面内有5个点A,B,C,D,E,直线与直线正好相交于点E,在这5个点中,过其中3个点能确定一个圆的概率是 .
13.小涵同学家开了一家超市,9月份盈利元,月份盈利达到元,每月盈利的平均增长率都相同,设每月盈利的平均增长率为x,则可列方程为 .
14.如图,是的直径,是上一点,若,则 .
15.如图,P为外一点,与相切于点A,交于点B,交于点C,,,则的半径为 .
16.杭州亚运会开幕式出现一座古今交汇拱底桥,桥面呈拱形.该桥的中间拱洞可以看成一种特殊的圆拱桥,此圆拱桥的跨径(桥拱圆弧所对的弦的长)约为,拱高(桥拱圆弧的中点到弦的距离)约为,则此桥拱的半径是 .
三、解答题
17.解方程:
(1)
(2)
18.小明和小亮用如图所示的同一个转盘进行“配紫色”游戏.游戏规则如下:连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色),则小明得1分,否则小亮得1分.你认为这个游戏对双方公平吗?请说明理由.若不公平,请你修改规则使游戏对双方公平.
19.已知关于的一元二次方程.
(1)求证:对于任意实数,该方程总有实数根;
(2)若这个一元二次方程的一根大于2,求的取值范围.
20.学校为了让同学们走向操场、积极参加体育锻炼,启动了“学生阳光体育运动”,张明和李亮在体育运动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
平均数 中位数 方差
张明 13.3 0.004
李亮 13.3
(1)张明成绩的平均数为: ;李亮成绩的中位数为: ;李亮成绩的方差为 ;
(2)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.
21.如图,在中,,以为直径的与交于点,过作的切线交的延长线于,交于.
(1)求证:;
(2)已知,,求的半径.
22.如1图是一款利用曲边三角形制造的扫地机. 如2 图是一个曲边三角形,它可按照如下方法作出:作等边三角形,分别以点A,B,C为圆心, 以的长为半径作,,,三段弧所围成的图形就是曲边三角形. 若这个曲边三角形的周长为,求它的面积(结果保留π).
23.如图,已知弓形的弦长,弓高,(,并经过圆心).
(1)请利用尺规作图的方法找到圆心;(保留作图痕迹,不必写作法)
(2)求弓形所在的半径的长.
参考答案:
1.C
【分析】根据一元二次方程的定义逐项判断即可得出答案.
【详解】解:中含有两个未知数,因此不是一元二次方程,故A选项不合题意;
不是整式方程,因此不是一元二次方程,故B选项不合题意;
中只含有一个未知数,未知数的最高次数是2,并且是整式方程,因此是一元二次方程,故C选项符合题意;
中含有两个未知数,因此不是一元二次方程,故D选项不合题意;
故选C.
【点睛】本题考查一元二次方程的识别,解题的关键是掌握定义,即通过化简后,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的整式方程,叫做一元二次方程.
2.B
【分析】本题考查了简单的概率计算.熟练掌握概率公式计算概率是解题的关键.
根据概率公式计算求解即可.
【详解】解:由题意知,小康恰好选中“陶艺”的概率为,
故选:B.
3.C
【分析】本题主要考查解一元二次方程的根,将代入方程即可求解,掌握解一元二次方程的根的计算方法是解题的关键.
【详解】解:根据题意,将代入方程得,
,
解得,,
故选:.
4.D
【分析】本题考查由实际问题抽象出一元二次方程的知识,可先表示出去年水蜜桃的亩产量,那么去年水蜜桃的亩产量,把相应数值代入即可求解.
【详解】解:去年水蜜桃的亩产量为,今年水蜜桃的亩产量在去年水蜜桃的亩产量的基础上增加x,为,
则列出的方程是,
故选:D.
5.C
【分析】本题主要考查平均数和样本容量的定义及方差,熟练掌握平均数和样本容量的定义及方差是解题的关键.
根据平均数的概念和样本容量指的是一个样本中所包含的单位数及方差公式的意义可直接进行求解.
【详解】解:∵一组数据的方差公式是
∴这组数据的平均数为45,样本容量为50.
故选C.
6.C
【分析】根据直径对的圆周角为直角得到,再根据同圆中同弧对的圆周角相等得到,即可求出.
此题主要考查了圆周角定理.熟练掌握直径所对的圆周角是直角,同圆中同弧所对的圆周角相等,是解决问题的关键.
【详解】∵为⊙O的直径,
∴,
∵,
∴.
故选:C.
7.B
【分析】本题考查的是垂线段最短的应用,垂径定理的应用,求解弧长,先过作交于,交弧于,可得此时最短,则最长,即为的位置,为的位置,再结合垂径定理与弧长公式可得答案.
【详解】解:如图,过作交于,交弧于,
此时最短,则最长,即为的位置,为的位置,
∴,,
∵,
∴的长度为:,
即的长度为:;
故选B
8.A
【分析】本题考查切线长定理,熟练掌握切线长定理是解题的关键.根据切线长定理得到,,,根据即可得到的周长.
【详解】解:∵的内切圆分别与,,相切于点D,E,F,且,
∴,,,
∵,
∴,
∴的周长,
故选:A.
9.
【分析】本题考查了一元二次方程的一般形式;
移项后将一元二次方程化为一般形式,然后可得答案.
【详解】解:将方程化为一般形式为,
其常数项为.
故答案为:.
10.
【分析】此题主要考查了方差的求法,解决问题的关键是对方差公式的正确应用.根据已知条件个数据的平方和是,平均数是,可知应该应用求方差公式推导出代入求出即可.
【详解】解:根据求方差公式:
,
故答案为:.
11.或
【分析】本题主要考查坐标与图形,切线的性质,一次函数图象与性质等知识,作轴于点E,交直线于点F,切点为点G,直线与y轴交点为Q,求得,证明,,由勾股定理得从而可求出点P在第三象限内的坐标,根据对称性可求出点P在第四象限的坐标.
【详解】解:如图,当点P在第三象限时,
对于,当时,则
作轴于点E,交直线于点F,则
解得,
∴,
∵与相切,
∴
又
∴,
∴
在中,由勾股定理得,,
∴点P的坐标为
∴;
同理可得,点P在第四象限内点的坐标为
∴,
综上,m的值为或
故答案为:或.
12.
【分析】此题考查确定圆的条件:经过不在同一条直线上的三个点确定一个圆;概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种可能,那么事件A的概率.
首先求出五个点任意选取3个点有10种情况,然后根据不在同一条直线上的三个点确定一个圆,所以过其中3个点能确定一个圆的情况有8种,由此求出概率.
【详解】解答:解:平面内有五个点A、B、C、D、E,任选3点有10种情况::A、E、B;A、E、C;A、E、D;A、B、C;A、B、D;C、D、E;B、E、C;B、E、D;A、D、C;B、D、C,
在这五个点中,过其中3个点能确定一个圆的情况是:A、E、C;A、E、D;A、B、C;A、B、D;B、E、C;B、E、D;A、D、C;B、D、C,共8种;
∴概率为:.
故答案为:.
13.
【分析】本题考查了一元二次方程的应用.根据题意正确的列方程是解题的关键.
由题意知,月份盈利,月份盈利,依题意可列方程,然后作答即可.
【详解】解:依题意得,,
故答案为:.
14.
【分析】本题考查圆周角定理,根据“同弧所对的圆周角是圆心角的一半”直接求解即可得到答案,熟记圆周角定理是解决问题的关键.
【详解】解:,
,
故答案为:.
15.6
【分析】本题主要考查了切线的性质得性质与判定,切线长定理,勾股定理,连接,先证明是的切线,进而由切线长定理得到,再由切线的性质得到,利用勾股定理求出,则,设的半径为r,则,在中,由勾股定理得,解方程即可得到答案.
【详解】解:如图所示,连接,
∵,是的半径,
∴是的切线,
∵与相切于点A,
∴,,
在中,由勾股定理得,
∴,
设的半径为r,则,
在中,由勾股定理得,
∴,
解得,
∴的半径为6,
故答案为:6.
16.
【分析】本题主要考查了垂径定理、勾股定理及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.设圆心为,作于点的延长线交圆弧为点,设半径为,根据垂径定理得,,由勾股定理得∶,即可求出答案.
【详解】解:如图,设圆心为,作于点的延长线交圆弧为点,则为优弧的中点,设半径为,
由勾股定理得∶,
解得∶,
故答案为:.
17.(1)
(2)
【分析】本题考查求解一元二次方程.掌握各类求解方法是解题关键.
(1)利用因式分解法即可求解;
(2)利用配方法即可求解.
【详解】(1)解:
,
,;
(2)解:
,
18.游戏不公平,如若两次转出颜色相同或配成紫色.则小明得4分.否则小亮得5分
【分析】本题考查的是概率,熟记概率等于所求情况数与总情况数之比是解题关键.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平﹒游戏是否公平,关键要看是否游戏双方赢的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
【详解】列表如下:
第一次 第二次 红 黄 蓝
红 (红,红) (红,黄) (红,蓝)
黄 (黄,红) (黄,黄) (黄.蓝)
蓝 (蓝,红) (蓝.黄) (蓝,蓝)
由表知,P(小明获胜),P(小亮获胜).
小明的得分为;小亮的得分为.
,
∴游戏不公平.如若两次转出颜色相同或配成紫色.则小明得4分.否则小亮得5分.
19.(1)见解析;
(2).
【分析】本题考查了根的判别式及解一元二次方程,正确运用判别式是解题的关键:
(1)根据一元二次方程判别式为,即可解答;
(2)解方程,求得,,根据题意得到,解不等式即可.
【详解】(1)证明:∵关于x的一元二次方程,
∴,
∴对于任意实数m,该方程总有实数根;
(2)解:设方程的两个实数根为,,
,
∴,,
∵这个一元二次方程的一根大于2,
∴,
解得:,
∴m的取值范围.
20.(1)13.3,13.3,0.02
(2)选择张明参加比赛,理由见解析
【分析】本题考查了平均数,中位数,方差的意义:
(1)利用平均数的计算公式可得出张明成绩的平均数;先将李亮的成绩按照从小到大排列,然后即可得到这组数据的中位数;
(2)在平均数、中位数相同的情况下,再根据方差越小数据越稳定,即可得出答案.
【详解】(1)解:张明成绩的平均数为:(秒);
李亮的成绩是:13.2,13.4,13.1,13.5,13.3,
把这些数从小到大排列为:13.1,13.2,13.3,13.4,13.5,
则李亮成绩的中位数是:13.3秒;
李亮的方差为:
故答案为:13.3,13.3,0.02;
(2)解: 选择张明参加比赛,理由如下:
因为张明和李亮成绩的平均数、中位数都相同,但张明成绩的方差小于李亮成绩的方差,张明成绩比李亮成绩稳定.
21.(1)见解析
(2)
【分析】本题考查的是切线的性质、勾股定理的应用,掌握圆的切线垂直于经过切点的半径是解题的关键.
(1)连接,根据切线的性质可得,再由,,可得,从而得到,即可;
(2)设的半径为r,在中,根据勾股定理,即可求解.
【详解】(1)证明:如图,连接,
∵是的切线,
∴,即,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
(2)设的半径为r,则,
∵,
∴,
在中,,,
∴,
解得:,
即的半径为.
22.
【分析】本题考查扇形面积的计算、等边三角形的性质、弧长的计算,根据题意和图形,可以计算出的长,然后根据扇形面积公式和三角形的面积,可以求得曲边三角形的面积.
【详解】解:由题意可得,
,,
∴,
解得,,
∵是等边三角形,
∵,
作交于点D,
∴,
∴,
∴,
∴一个曲边三角形的面积是:.
23.(1)详见解析
(2)10
【分析】本题考查作图-复杂作图,垂径定理,解直角三角形等知识,解题的关键是理解题意,学会利用参数构建方程解决问题,属于中考常考题型.
(1)作线段的垂直平分线交直线于点O,点O即为所求.
(2)连接,利用垂径定理和勾股定理即可求出.
【详解】(1)解:如图所示,作线段的垂直平分线交直线于点O,点即是圆心;
(2)连接,
,并经过圆心,,
,在中,由勾股定理得:
解得,,
答:的半径的长为10.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
