期末易错精选题-2023-2024学年数学八年级上册苏科版(含解析)
文档属性
| 名称 | 期末易错精选题-2023-2024学年数学八年级上册苏科版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 20:48:29 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末易错精选题-2023-2024学年数学八年级上册苏科版
一、单选题
1.点A,B的坐标分别为,,点P在x轴上,的值最小时,点P的坐标为( ).
A. B. C. D.
2.已知一次函数的图象不过第三象限,则的取值范围是( )
A. B. C. D.
3.已知点和点都在直线上,若,则的关系( )
A. B. C. D.不能比较
4.如图,和中,,,添加下列哪一个条件无法证明( )
A. B. C. D.
5.如图,在中,的垂直平分线交于点,边的垂直平分线交于点.已知的周长为,则的长为( )
A. B. C. D.
6.将个面积都是的正方形按如图所示的方法摆放,点、……分别是各正方形的中心,则个这样的正方形重叠部分(阴影部分)的面积和为( )
A. B. C. D.
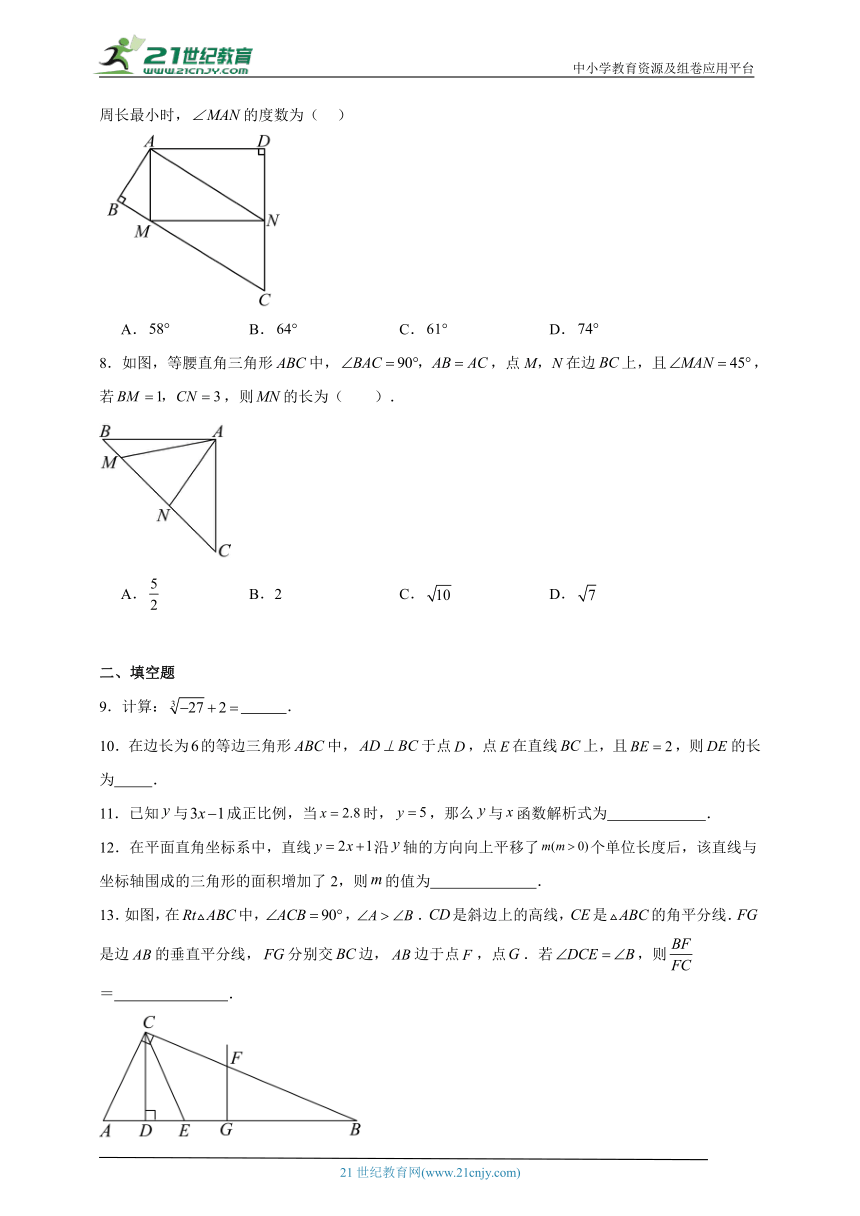
7.四边形中,,,在上分别找一点M、N,当的周长最小时,的度数为( )
A. B. C. D.
8.如图,等腰直角三角形中,,点M,N在边上,且,若,则的长为( ).
A. B.2 C. D.
二、填空题
9.计算: .
10.在边长为的等边三角形中,于点,点在直线上,且,则的长为 .
11.已知与成正比例,当时,,那么与函数解析式为 .
12.在平面直角坐标系中,直线沿轴的方向向上平移了个单位长度后,该直线与坐标轴围成的三角形的面积增加了2,则的值为 .
13.如图,在中,,.是斜边上的高线,是的角平分线.是边的垂直平分线,分别交边,边于点,点.若,则= .
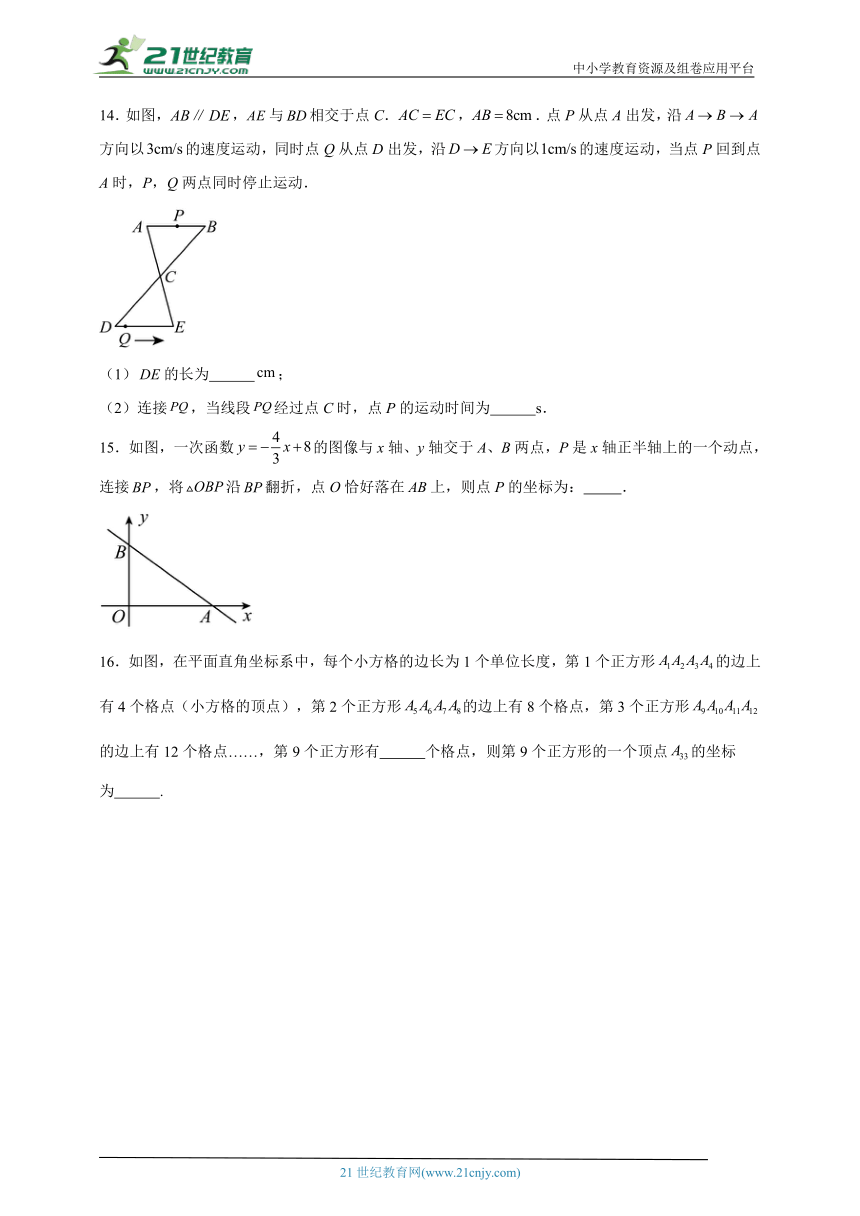
14.如图,,与相交于点C.,.点P从点A出发,沿方向以的速度运动,同时点Q从点D出发,沿方向以的速度运动,当点P回到点A时,P,Q两点同时停止运动.
(1)的长为 ;
(2)连接,当线段经过点C时,点P的运动时间为 s.
15.如图,一次函数的图像与x轴、y轴交于A、B两点,P是x轴正半轴上的一个动点,连接,将沿翻折,点O恰好落在上,则点P的坐标为: .
16.如图,在平面直角坐标系中,每个小方格的边长为1个单位长度,第1个正方形的边上有4个格点(小方格的顶点),第2个正方形的边上有8个格点,第3个正方形的边上有12个格点……,第9个正方形有 个格点,则第9个正方形的一个顶点的坐标为 .
三、解答题
17.已知:的立方根是3,的算术平方根是2,c的平方根是它本身.
(1)求a,b,c的值;
(2)求的平方根.
18.在中,,,点M为的中点,连接,点D为线段上一动点,过点D作,且,(点E在的上方),连接,过点E作的垂线交边于点F.
(1)如图1,当点D为的中点时,
①依题意补全图形;
②直接写出和的数量关系为______;
(2)当点D在图2的位置时,用等式表示线段和之间的数量关系,并证明.
19.在学习等腰三角形的性质时,林林进一步探究发现:三角形一个角的平分线与其对边的高重合时,这个三角形是等腰三角形,他通过证明三角形全等得到结论,请根据他的思路完成以下作图与填空:
(1)用直尺和圆规,作的角平分线交于D.(只保留作图痕迹)
(2)已知:如图:在中,是的角平分线,.
求证:.
证明:是的角平分线,
①___________.
,
②____________,
,
③__________.
林林根据垂直平分线的性质进一步发现:三角形一边上的④________________重合时,这个三角形是等腰三角形.
20.如图,在平面直角坐标系中,的三个顶点的坐标分别为 .
(1)画出关于x轴对称的;
(2)点的坐标为 ,点的坐标为 ;
(3)点与点Q关于y轴对称,若,求点P的坐标.
21.荡秋千(图1)是中国古代北方少数民族创造的一种运动. 有一天,赵彬在公园里游玩,如图2,他发现秋千静止时,踏板离地的垂直高度 ,将它往前推送 (水平距离 )时,秋千的踏板离地的垂直高度,秋千的绳索始终拉得很直,求绳索的长度.
22.如图①,在中,,G为三角形外一点,且为等边三角形.
(1)求证:直线垂直平分;
(2)以为一边作等边三角形(如图②),连接,.若,,求的长.
23.如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,已知点,点,直线经过点.
(1)请计算的面积.
(2)求直线的解析式.
(3)若在x轴上有一动点,当线段的长度最小时,求此时点的坐标.
24.如图,直线与x轴、y轴分别交于点A、点B,点P是射线上的动点,过点B作直线的垂线交x轴于点Q,垂足为点C,连接.
(1)当点P在线段上时,
①求证:;
②若点P为的中点,求的面积.
(2)在点P的运动过程中,是否存在某一位置,使得成为等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.
参考答案:
1.C
【分析】考查最短路线问题,得到点A关于x轴的对称点的坐标,可得到直线的解析式,求得与x轴的交点即为所求点的坐标.
【详解】解:∵点,
∴点A关于x轴的对称点的坐标为,
设直线的解析式为
,
解得
∴
∴P的坐标为.
故选:C.
2.D
【分析】本题主要考查了一次函数图象与系数的关系,要熟练掌握,根据一次函数的图象不经过第三象限,可得,据此求出m的取值范围即可.
【详解】解:∵一次函数的图象不经过第三象限,
∴,
解得:,故D正确.
故选:D.
3.C
【分析】本题主要考查了比较一次函数值的大小,根据一次函数解析式可得在中y随x增大而增大,据此可得答案.
【详解】解:∵在中,,
∴在中y随x增大而增大,
∵点和点都在直线上,且,
∴,
故选C.
4.C
【分析】本题考查了全等三角形的判定,平行线的性质,熟练掌握三角形全等的判定方法是解题的关键.根据全等三角形的判定方法对各选项分析判断即可得解.
【详解】解:A、可以求出,符合“” 能证明,故A选项不符合题意;
B、时符合“”能证明;故B选项不符合题意;
C、是“”,不能证明,故C选项符合题意;
D、由可得,符合“”,能证明,故D选项不符合题意.
故选:C.
5.D
【分析】本题主要考查了线段垂直平分线的性质,利用线段垂直平分线的性质可得,,然后利用等量代换可得的周长,即可解答.
【详解】解:∵是的垂直平分线,
∴,
∵是的垂直平分线,
∴,
∵的周长,
∴,
∴,
∴,
∴的长为;
故选D.
6.D
【分析】本题考查了正方形中的规律,根据每个阴影面积是正方形面积的即,根据规律一共有n个,计算即可.
【详解】如图,设第一个正方形的一个顶点为F,两个正方形的边的交点分别为点D和点E,过点作于点B,作于点C,
∵是正方形的中心,且每个大正方形的面积都是2,
∴,四边形是正方形,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,
∵两个正方形构成一个1阴影,3个正方形构成2个阴影,4个正方形构成3个阴影,
∴个正方形构成n个阴影,
∴它们的和为,
故选:D.
7.B
【分析】本题考查对称的性质、线段垂直平分线的性质、三角形内角和定理等知识,利用对称作辅助线是解决最短的关键.
延长到使得,延长到使得,连接与分别交于点M、N,此时周长最小,推出,进而得出的度数.
【详解】解:如图,延长到使得,延长到使得,连接与分别交于点M、N.
,
关于对称,关于对称,
此时的周长最小,
,
,
同理:,
,
,
,
,
,
.
,
故选:B.
8.C
【分析】本题考查了等腰直角三角形的性质,全等三角形的判定与性质,勾股定理的运用,把沿翻折至,连接,则,,,,再证明得到, ,接着证明,则,.
【详解】解:把沿翻折至,连接,
∴,,,,
又∵,
∴,
∵,
,
∴,
又∵,
∴,
∴, ,
∴,
在中, ,
,
故选:C.
9.
【分析】本题考查了实数的混合运算,先求出立方根,再计算加减即可,熟练掌握实数的混合运算法则是解此题的关键.
【详解】解:,
故答案为:.
10.或
【分析】本题考查了等边三角形的性质和线段和差,由等腰三角形“三线合一”可得,再通过线段和差即可求解,解题的关键是熟练掌握等边三角形的性质的应用.
【详解】解:∵是等边三角形,,
∴,
∴或,
故答案为:或.
11.
【分析】此题考查了待定系数法求一次函数解析式;设出关系式,将,代入求出的值,即可确定出解析式,即可求解.
【详解】解:依题意,设,将,代入
,
解得:
∴
故答案为:.
12.2
【分析】本题考查一次函数的平移,一次函数的图象与坐标轴的交点问题.根据平移,得到新的函数解析式为,根据直线与坐标轴围成的三角形的面积增加了2,列出方程求解即可.
【详解】解:∵,
∴当时,,当时,,
∴直线与坐标轴的交点坐标为:,
∴直线与坐标轴围成的三角形的面积为;
把直线沿轴的方向向上平移了个单位长度后,得到的新函数解析式为:,
当时,,当时,,
∴∴直线与坐标轴的交点坐标为:,
∴直线与坐标轴围成的三角形的面积为;
∴,
∴,
∴或(不合题意,舍去);
故答案为:2.
13.
【分析】连接,根据是斜边上的高线,易证.由角平分线定义可求出,即可得出.由是边的垂直平分线,即可得出,从而可得出,再由三角形外角性质可求出,即证明为等腰直角三角形,结合勾股定理即得出.
【详解】如图,连接,
∵是斜边上的高线,
∴.
∵,
∴,
∴,
∴.
∵是的平分线,
∴,
∴,
∴.
∵是边的垂直平分线,
∴,
∴,
∴,
∴为等腰直角三角形,
∴,即.
故答案为:.
【点睛】本题考查角平分线定义,线段垂直平分线的性质,三角形外角性质,等腰直角三角形的判定和性质以及勾股定理.连接常用的辅助线是解题关键.
14. 8 2或4
【分析】本题考查全等三角形的判定与性质,解题的关键是注意分情况讨论.
(1)证,可得答案;
(2)当线段经过点C时,证明,推出,分点P沿方向运动和沿方向运动两种情况,分别列式求解.
【详解】解:(1)∵,
∴,
在和中,
,
,
,
(2)当线段经过点C时,如下图所示:
在和中,
,
,
,
当点P沿方向运动时,,,
,
,
解得;
当点P沿方向运动时,,,
,
,
解得;
综上可知,t的值为或,
故答案为:(1)8;(2)2或4.
15.
【分析】此题主要考查了翻折的性质,勾股定理,一次函数与坐标轴的交点及应用,正确掌握各知识点是解题的关键.根据一次函数的解析式求出点A,B的坐标,根据勾股定理求出,由翻折的性质得到,,设,根据勾股定理,列方程求出,得到.
【详解】解:令中,得;令,得,
∴,
∴,
根据勾股定理得,
∵将沿翻折,点恰好落在上的点D处,
∴,,
∴,
设,则,
根据勾股定理,
∴,
解得,
∴.
故答案为:.
16. 36
【分析】本题考查了点的坐标的规律的探究,观察图形并得出点的坐标的特点是解题关键.每个正方形上有4个顶点,由正方向边上格点数得到规律,再判断顶点应为,根据顶点规律即可得出答案.
【详解】解:由题可知,第1个正方形的边上有4个格点;第2个正方形的边上有8个格点;第3个正方形的边上有12个格点;则第个正方形的边上有个格点,
∴第9个正方形有个格点;
∵点的坐标为,点的坐标为,点的坐标为,
∴第9个正方形的一个顶点的坐标为.
故答案为:36;.
17.(1),,
(2)
【分析】(1)根据立方根,算术平方根,平方根的概念即可求出答案;
(2)根据(1)中所求,,的值代入代数式中即可求出答案.
【详解】(1)解:根据题意可得:,,,
,,;
(2),,
,
∴的平方根为,
即的平方根为.
【点睛】本题主要考查了立方根、平方根、算术平方根及代数式的求值,熟练掌握相关概念进行求解是解决本题的关键.
18.(1)①见解析;②
(2)当点D在图2位置时,仍满足,见解析
【分析】(1)①根据题意补全图形即可;②分别证明,是等腰直角三角形,利用等腰直角三角形的性质即可证明;
(2)设与交于点N,连接,证明,利用等腰三角形的性质即可证明.
【详解】(1)解:①补图.
②如图1,过点E作的垂线交边于点F.
,,点M为的中点,
,,
,
是等腰直角三角形,
点M,F重合,
,
,
是等腰直角三角形,
,且,
,
,
故答案为:;
(2)解:当点D在图2位置时,仍满足,
证明:如图,设与交于点N,连接,
∵,,M为中点,
∴,,
∵,,
∴,
在与中,
,
∴,
∴,
∵在和中,,,,
∴(即),
∴,
∴,
∵,
∴,
∵,
∴.
【点睛】本题是三角形综合题目,考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的性质等知识;本题综合性强,熟练掌握等腰直角三角形的判定与性质,证明三角形全等是解题的关键.
19.(1)详见解析;
(2)高与中线.
【分析】本题考查了作图 基本作图,等腰三角形判定与性质,全等三角形的判定与性质等知识点,
(1)根据角平分线的基本作法作出图形即可;
(2)根据证明即可得出结论;
证明是解题的关键.
【详解】(1)如图所示;
(2)∵是的角平分线,
∴,
∵,
∴,
∵
∴.
∴.
林林根据垂直平分线的性质进一步发现:三角形一边上的高与中线重合时,这个三角形是等腰三角形,
故答案为:高与中线.
20.(1)图见解析
(2),
(3)点P的坐标为(4,2)或(﹣4,﹣6)
【分析】本题主要考查了坐标与图形变化—轴对称,熟知关于x轴对称,关于y轴对称的点的坐标特征是解题的关键.
(1)首先确定,,三点关于轴对称点的位置,然后依次连接即可;
(2)根据(1)所画图形写出对应点坐标即可;
(3)根据点关于关于轴对称的点的坐标为,即可确定点的坐标,再由,求出a的值,进而确定点的坐标.
【详解】(1)解:如图所示,即为所求;
(2)解:由图可知,,,
故答案为:,;
(3)解:∵点与点关于轴对称,
∴点的坐标为,
又∵,
∴,
∴或,
∴当时,;当时,,
∴点的坐标为或.
21.
【分析】本题考查了勾股定理的应用,设绳索的长度为,则,在中,由勾股定理得出方程,解方程即可.由勾股定理得出方程是解题的关键.
【详解】解:由题意得:,
在中,由勾股定理得:,
设绳索的长度为,则,
∴,
解得:,
答:绳索的长度是.
22.(1)证明见解析
(2)4
【分析】本题主要考查了全等三角形的判定和性质,等边三角形的性质以及勾股定理,熟练掌握全等三角形的判定和性质是解题的关键.
(1)由,证明即可;
(2)证明,由全等三角形的性质证明,由勾股定理计算即可.
【详解】(1)证明:为等边三角形,
,
点G在的垂直平分线上,
又,
点A在垂直平分线上,
直线垂直平分;
(2)解:和为等边三角形,
,
,
在和中,
,
,
,
,
,
,
,
.
23.(1)3
(2)
(3)
【分析】本题是一次函数的综合题,涉及最短路径问题,待定系数法求函数解析式,坐标轴上点的坐标特征,解题的关键是掌握待定系数法求一次函数的解析式.
(1)由点得,由点得的边上的高为,利用三角形的面积公式即可求解;
(2)利用待定系数法可求得直线的解析式;
(3)作点关于轴的对称点,则点的坐标,连接与轴交于点,根据最短路径问题得:此时,线段的长度最小,由直线经过点得点,利用待定系数法可求得直线的解析式,根据轴上点的坐标特征求出点的坐标.
【详解】(1)解:,点.
,的边上的高为,
;
(2)直线与轴交于点,与轴交于点,已知点,点,
,
解得,
直线的解析式为;
(3)作点关于轴的对称点,连接与轴交于点,此时,线段的长度最小,
,
点的坐标,
直线经过点.
,
点,
设直线的解析式为,
则,
解得,
直线的解析式为,
点在轴上,当时,,
点的坐标为.
24.(1)①见解析,②
(2)或或
【分析】本题考查了一次函数与几何图形综合,熟练掌握全等三角形的性质与判定,坐标与图形是解题的关键.
(1)①根据一次函数解析式得出,根据垂直关系以及等角的余角相等,得出,进而证明;
②由①知:,则,直线的解析式为:,同理可得:直线的解析式为:,联立得出,进而根据三角形面积公式即可求解;
(2)分当点在线段上时,当点在的延长线上时,根据等腰三角形的定义,即可求解.
【详解】(1)①证明:当时,,
,
当时,,
,
,
,
,
,
,
,
,
,
,
;
②解:,点是 的中点,
,
由①知:,
,
,
设直线的解析式为:,
,
,
同理可得:直线的解析式为:,
由得,
,
,
;
(2)解:如图1,
当点在线段上时,
若,由于,则有,
即当时,是等腰三角形;,
若,由于,则有,
过点C作轴于点H,显然,
即不可能,
当是等腰三角形时,只有,
,
,
,,
,
,
,
,
,
,
如图2,
当点在的延长线上时,
同理可得:,
综上所述:或或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末易错精选题-2023-2024学年数学八年级上册苏科版
一、单选题
1.点A,B的坐标分别为,,点P在x轴上,的值最小时,点P的坐标为( ).
A. B. C. D.
2.已知一次函数的图象不过第三象限,则的取值范围是( )
A. B. C. D.
3.已知点和点都在直线上,若,则的关系( )
A. B. C. D.不能比较
4.如图,和中,,,添加下列哪一个条件无法证明( )
A. B. C. D.
5.如图,在中,的垂直平分线交于点,边的垂直平分线交于点.已知的周长为,则的长为( )
A. B. C. D.
6.将个面积都是的正方形按如图所示的方法摆放,点、……分别是各正方形的中心,则个这样的正方形重叠部分(阴影部分)的面积和为( )
A. B. C. D.
7.四边形中,,,在上分别找一点M、N,当的周长最小时,的度数为( )
A. B. C. D.
8.如图,等腰直角三角形中,,点M,N在边上,且,若,则的长为( ).
A. B.2 C. D.
二、填空题
9.计算: .
10.在边长为的等边三角形中,于点,点在直线上,且,则的长为 .
11.已知与成正比例,当时,,那么与函数解析式为 .
12.在平面直角坐标系中,直线沿轴的方向向上平移了个单位长度后,该直线与坐标轴围成的三角形的面积增加了2,则的值为 .
13.如图,在中,,.是斜边上的高线,是的角平分线.是边的垂直平分线,分别交边,边于点,点.若,则= .
14.如图,,与相交于点C.,.点P从点A出发,沿方向以的速度运动,同时点Q从点D出发,沿方向以的速度运动,当点P回到点A时,P,Q两点同时停止运动.
(1)的长为 ;
(2)连接,当线段经过点C时,点P的运动时间为 s.
15.如图,一次函数的图像与x轴、y轴交于A、B两点,P是x轴正半轴上的一个动点,连接,将沿翻折,点O恰好落在上,则点P的坐标为: .
16.如图,在平面直角坐标系中,每个小方格的边长为1个单位长度,第1个正方形的边上有4个格点(小方格的顶点),第2个正方形的边上有8个格点,第3个正方形的边上有12个格点……,第9个正方形有 个格点,则第9个正方形的一个顶点的坐标为 .
三、解答题
17.已知:的立方根是3,的算术平方根是2,c的平方根是它本身.
(1)求a,b,c的值;
(2)求的平方根.
18.在中,,,点M为的中点,连接,点D为线段上一动点,过点D作,且,(点E在的上方),连接,过点E作的垂线交边于点F.
(1)如图1,当点D为的中点时,
①依题意补全图形;
②直接写出和的数量关系为______;
(2)当点D在图2的位置时,用等式表示线段和之间的数量关系,并证明.
19.在学习等腰三角形的性质时,林林进一步探究发现:三角形一个角的平分线与其对边的高重合时,这个三角形是等腰三角形,他通过证明三角形全等得到结论,请根据他的思路完成以下作图与填空:
(1)用直尺和圆规,作的角平分线交于D.(只保留作图痕迹)
(2)已知:如图:在中,是的角平分线,.
求证:.
证明:是的角平分线,
①___________.
,
②____________,
,
③__________.
林林根据垂直平分线的性质进一步发现:三角形一边上的④________________重合时,这个三角形是等腰三角形.
20.如图,在平面直角坐标系中,的三个顶点的坐标分别为 .
(1)画出关于x轴对称的;
(2)点的坐标为 ,点的坐标为 ;
(3)点与点Q关于y轴对称,若,求点P的坐标.
21.荡秋千(图1)是中国古代北方少数民族创造的一种运动. 有一天,赵彬在公园里游玩,如图2,他发现秋千静止时,踏板离地的垂直高度 ,将它往前推送 (水平距离 )时,秋千的踏板离地的垂直高度,秋千的绳索始终拉得很直,求绳索的长度.
22.如图①,在中,,G为三角形外一点,且为等边三角形.
(1)求证:直线垂直平分;
(2)以为一边作等边三角形(如图②),连接,.若,,求的长.
23.如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,已知点,点,直线经过点.
(1)请计算的面积.
(2)求直线的解析式.
(3)若在x轴上有一动点,当线段的长度最小时,求此时点的坐标.
24.如图,直线与x轴、y轴分别交于点A、点B,点P是射线上的动点,过点B作直线的垂线交x轴于点Q,垂足为点C,连接.
(1)当点P在线段上时,
①求证:;
②若点P为的中点,求的面积.
(2)在点P的运动过程中,是否存在某一位置,使得成为等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.
参考答案:
1.C
【分析】考查最短路线问题,得到点A关于x轴的对称点的坐标,可得到直线的解析式,求得与x轴的交点即为所求点的坐标.
【详解】解:∵点,
∴点A关于x轴的对称点的坐标为,
设直线的解析式为
,
解得
∴
∴P的坐标为.
故选:C.
2.D
【分析】本题主要考查了一次函数图象与系数的关系,要熟练掌握,根据一次函数的图象不经过第三象限,可得,据此求出m的取值范围即可.
【详解】解:∵一次函数的图象不经过第三象限,
∴,
解得:,故D正确.
故选:D.
3.C
【分析】本题主要考查了比较一次函数值的大小,根据一次函数解析式可得在中y随x增大而增大,据此可得答案.
【详解】解:∵在中,,
∴在中y随x增大而增大,
∵点和点都在直线上,且,
∴,
故选C.
4.C
【分析】本题考查了全等三角形的判定,平行线的性质,熟练掌握三角形全等的判定方法是解题的关键.根据全等三角形的判定方法对各选项分析判断即可得解.
【详解】解:A、可以求出,符合“” 能证明,故A选项不符合题意;
B、时符合“”能证明;故B选项不符合题意;
C、是“”,不能证明,故C选项符合题意;
D、由可得,符合“”,能证明,故D选项不符合题意.
故选:C.
5.D
【分析】本题主要考查了线段垂直平分线的性质,利用线段垂直平分线的性质可得,,然后利用等量代换可得的周长,即可解答.
【详解】解:∵是的垂直平分线,
∴,
∵是的垂直平分线,
∴,
∵的周长,
∴,
∴,
∴,
∴的长为;
故选D.
6.D
【分析】本题考查了正方形中的规律,根据每个阴影面积是正方形面积的即,根据规律一共有n个,计算即可.
【详解】如图,设第一个正方形的一个顶点为F,两个正方形的边的交点分别为点D和点E,过点作于点B,作于点C,
∵是正方形的中心,且每个大正方形的面积都是2,
∴,四边形是正方形,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,
∵两个正方形构成一个1阴影,3个正方形构成2个阴影,4个正方形构成3个阴影,
∴个正方形构成n个阴影,
∴它们的和为,
故选:D.
7.B
【分析】本题考查对称的性质、线段垂直平分线的性质、三角形内角和定理等知识,利用对称作辅助线是解决最短的关键.
延长到使得,延长到使得,连接与分别交于点M、N,此时周长最小,推出,进而得出的度数.
【详解】解:如图,延长到使得,延长到使得,连接与分别交于点M、N.
,
关于对称,关于对称,
此时的周长最小,
,
,
同理:,
,
,
,
,
,
.
,
故选:B.
8.C
【分析】本题考查了等腰直角三角形的性质,全等三角形的判定与性质,勾股定理的运用,把沿翻折至,连接,则,,,,再证明得到, ,接着证明,则,.
【详解】解:把沿翻折至,连接,
∴,,,,
又∵,
∴,
∵,
,
∴,
又∵,
∴,
∴, ,
∴,
在中, ,
,
故选:C.
9.
【分析】本题考查了实数的混合运算,先求出立方根,再计算加减即可,熟练掌握实数的混合运算法则是解此题的关键.
【详解】解:,
故答案为:.
10.或
【分析】本题考查了等边三角形的性质和线段和差,由等腰三角形“三线合一”可得,再通过线段和差即可求解,解题的关键是熟练掌握等边三角形的性质的应用.
【详解】解:∵是等边三角形,,
∴,
∴或,
故答案为:或.
11.
【分析】此题考查了待定系数法求一次函数解析式;设出关系式,将,代入求出的值,即可确定出解析式,即可求解.
【详解】解:依题意,设,将,代入
,
解得:
∴
故答案为:.
12.2
【分析】本题考查一次函数的平移,一次函数的图象与坐标轴的交点问题.根据平移,得到新的函数解析式为,根据直线与坐标轴围成的三角形的面积增加了2,列出方程求解即可.
【详解】解:∵,
∴当时,,当时,,
∴直线与坐标轴的交点坐标为:,
∴直线与坐标轴围成的三角形的面积为;
把直线沿轴的方向向上平移了个单位长度后,得到的新函数解析式为:,
当时,,当时,,
∴∴直线与坐标轴的交点坐标为:,
∴直线与坐标轴围成的三角形的面积为;
∴,
∴,
∴或(不合题意,舍去);
故答案为:2.
13.
【分析】连接,根据是斜边上的高线,易证.由角平分线定义可求出,即可得出.由是边的垂直平分线,即可得出,从而可得出,再由三角形外角性质可求出,即证明为等腰直角三角形,结合勾股定理即得出.
【详解】如图,连接,
∵是斜边上的高线,
∴.
∵,
∴,
∴,
∴.
∵是的平分线,
∴,
∴,
∴.
∵是边的垂直平分线,
∴,
∴,
∴,
∴为等腰直角三角形,
∴,即.
故答案为:.
【点睛】本题考查角平分线定义,线段垂直平分线的性质,三角形外角性质,等腰直角三角形的判定和性质以及勾股定理.连接常用的辅助线是解题关键.
14. 8 2或4
【分析】本题考查全等三角形的判定与性质,解题的关键是注意分情况讨论.
(1)证,可得答案;
(2)当线段经过点C时,证明,推出,分点P沿方向运动和沿方向运动两种情况,分别列式求解.
【详解】解:(1)∵,
∴,
在和中,
,
,
,
(2)当线段经过点C时,如下图所示:
在和中,
,
,
,
当点P沿方向运动时,,,
,
,
解得;
当点P沿方向运动时,,,
,
,
解得;
综上可知,t的值为或,
故答案为:(1)8;(2)2或4.
15.
【分析】此题主要考查了翻折的性质,勾股定理,一次函数与坐标轴的交点及应用,正确掌握各知识点是解题的关键.根据一次函数的解析式求出点A,B的坐标,根据勾股定理求出,由翻折的性质得到,,设,根据勾股定理,列方程求出,得到.
【详解】解:令中,得;令,得,
∴,
∴,
根据勾股定理得,
∵将沿翻折,点恰好落在上的点D处,
∴,,
∴,
设,则,
根据勾股定理,
∴,
解得,
∴.
故答案为:.
16. 36
【分析】本题考查了点的坐标的规律的探究,观察图形并得出点的坐标的特点是解题关键.每个正方形上有4个顶点,由正方向边上格点数得到规律,再判断顶点应为,根据顶点规律即可得出答案.
【详解】解:由题可知,第1个正方形的边上有4个格点;第2个正方形的边上有8个格点;第3个正方形的边上有12个格点;则第个正方形的边上有个格点,
∴第9个正方形有个格点;
∵点的坐标为,点的坐标为,点的坐标为,
∴第9个正方形的一个顶点的坐标为.
故答案为:36;.
17.(1),,
(2)
【分析】(1)根据立方根,算术平方根,平方根的概念即可求出答案;
(2)根据(1)中所求,,的值代入代数式中即可求出答案.
【详解】(1)解:根据题意可得:,,,
,,;
(2),,
,
∴的平方根为,
即的平方根为.
【点睛】本题主要考查了立方根、平方根、算术平方根及代数式的求值,熟练掌握相关概念进行求解是解决本题的关键.
18.(1)①见解析;②
(2)当点D在图2位置时,仍满足,见解析
【分析】(1)①根据题意补全图形即可;②分别证明,是等腰直角三角形,利用等腰直角三角形的性质即可证明;
(2)设与交于点N,连接,证明,利用等腰三角形的性质即可证明.
【详解】(1)解:①补图.
②如图1,过点E作的垂线交边于点F.
,,点M为的中点,
,,
,
是等腰直角三角形,
点M,F重合,
,
,
是等腰直角三角形,
,且,
,
,
故答案为:;
(2)解:当点D在图2位置时,仍满足,
证明:如图,设与交于点N,连接,
∵,,M为中点,
∴,,
∵,,
∴,
在与中,
,
∴,
∴,
∵在和中,,,,
∴(即),
∴,
∴,
∵,
∴,
∵,
∴.
【点睛】本题是三角形综合题目,考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的性质等知识;本题综合性强,熟练掌握等腰直角三角形的判定与性质,证明三角形全等是解题的关键.
19.(1)详见解析;
(2)高与中线.
【分析】本题考查了作图 基本作图,等腰三角形判定与性质,全等三角形的判定与性质等知识点,
(1)根据角平分线的基本作法作出图形即可;
(2)根据证明即可得出结论;
证明是解题的关键.
【详解】(1)如图所示;
(2)∵是的角平分线,
∴,
∵,
∴,
∵
∴.
∴.
林林根据垂直平分线的性质进一步发现:三角形一边上的高与中线重合时,这个三角形是等腰三角形,
故答案为:高与中线.
20.(1)图见解析
(2),
(3)点P的坐标为(4,2)或(﹣4,﹣6)
【分析】本题主要考查了坐标与图形变化—轴对称,熟知关于x轴对称,关于y轴对称的点的坐标特征是解题的关键.
(1)首先确定,,三点关于轴对称点的位置,然后依次连接即可;
(2)根据(1)所画图形写出对应点坐标即可;
(3)根据点关于关于轴对称的点的坐标为,即可确定点的坐标,再由,求出a的值,进而确定点的坐标.
【详解】(1)解:如图所示,即为所求;
(2)解:由图可知,,,
故答案为:,;
(3)解:∵点与点关于轴对称,
∴点的坐标为,
又∵,
∴,
∴或,
∴当时,;当时,,
∴点的坐标为或.
21.
【分析】本题考查了勾股定理的应用,设绳索的长度为,则,在中,由勾股定理得出方程,解方程即可.由勾股定理得出方程是解题的关键.
【详解】解:由题意得:,
在中,由勾股定理得:,
设绳索的长度为,则,
∴,
解得:,
答:绳索的长度是.
22.(1)证明见解析
(2)4
【分析】本题主要考查了全等三角形的判定和性质,等边三角形的性质以及勾股定理,熟练掌握全等三角形的判定和性质是解题的关键.
(1)由,证明即可;
(2)证明,由全等三角形的性质证明,由勾股定理计算即可.
【详解】(1)证明:为等边三角形,
,
点G在的垂直平分线上,
又,
点A在垂直平分线上,
直线垂直平分;
(2)解:和为等边三角形,
,
,
在和中,
,
,
,
,
,
,
,
.
23.(1)3
(2)
(3)
【分析】本题是一次函数的综合题,涉及最短路径问题,待定系数法求函数解析式,坐标轴上点的坐标特征,解题的关键是掌握待定系数法求一次函数的解析式.
(1)由点得,由点得的边上的高为,利用三角形的面积公式即可求解;
(2)利用待定系数法可求得直线的解析式;
(3)作点关于轴的对称点,则点的坐标,连接与轴交于点,根据最短路径问题得:此时,线段的长度最小,由直线经过点得点,利用待定系数法可求得直线的解析式,根据轴上点的坐标特征求出点的坐标.
【详解】(1)解:,点.
,的边上的高为,
;
(2)直线与轴交于点,与轴交于点,已知点,点,
,
解得,
直线的解析式为;
(3)作点关于轴的对称点,连接与轴交于点,此时,线段的长度最小,
,
点的坐标,
直线经过点.
,
点,
设直线的解析式为,
则,
解得,
直线的解析式为,
点在轴上,当时,,
点的坐标为.
24.(1)①见解析,②
(2)或或
【分析】本题考查了一次函数与几何图形综合,熟练掌握全等三角形的性质与判定,坐标与图形是解题的关键.
(1)①根据一次函数解析式得出,根据垂直关系以及等角的余角相等,得出,进而证明;
②由①知:,则,直线的解析式为:,同理可得:直线的解析式为:,联立得出,进而根据三角形面积公式即可求解;
(2)分当点在线段上时,当点在的延长线上时,根据等腰三角形的定义,即可求解.
【详解】(1)①证明:当时,,
,
当时,,
,
,
,
,
,
,
,
,
,
,
;
②解:,点是 的中点,
,
由①知:,
,
,
设直线的解析式为:,
,
,
同理可得:直线的解析式为:,
由得,
,
,
;
(2)解:如图1,
当点在线段上时,
若,由于,则有,
即当时,是等腰三角形;,
若,由于,则有,
过点C作轴于点H,显然,
即不可能,
当是等腰三角形时,只有,
,
,
,,
,
,
,
,
,
,
如图2,
当点在的延长线上时,
同理可得:,
综上所述:或或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
