定积分的概念(二)

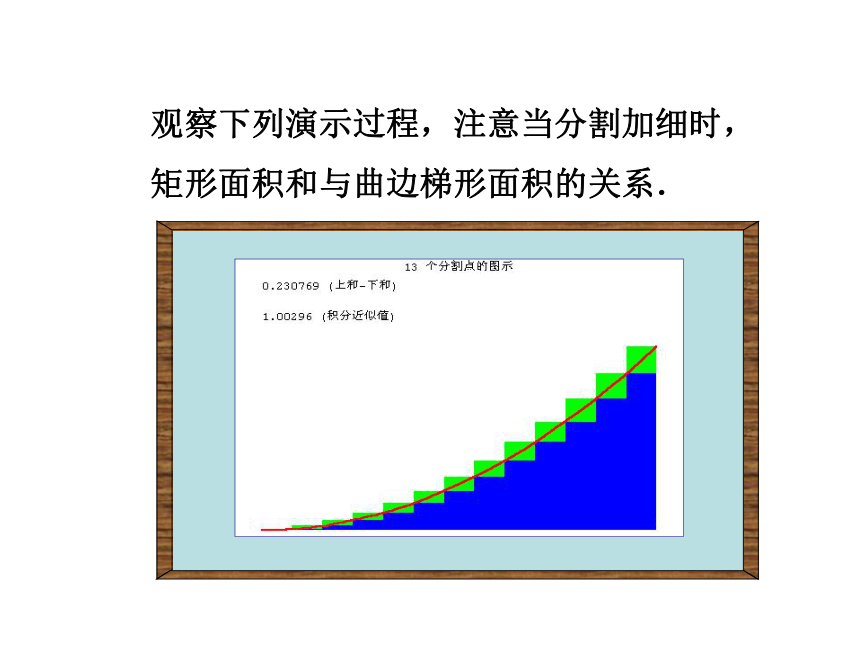
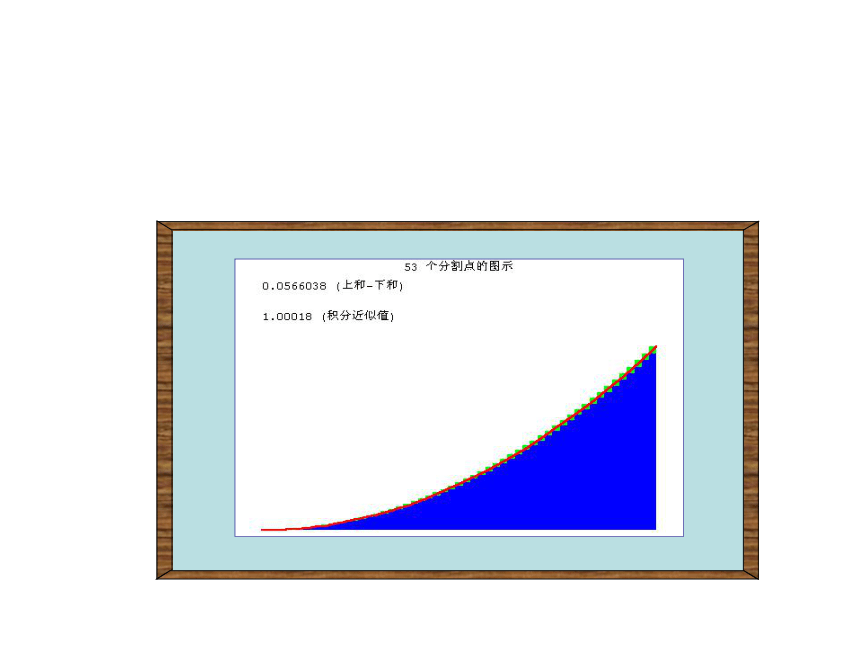
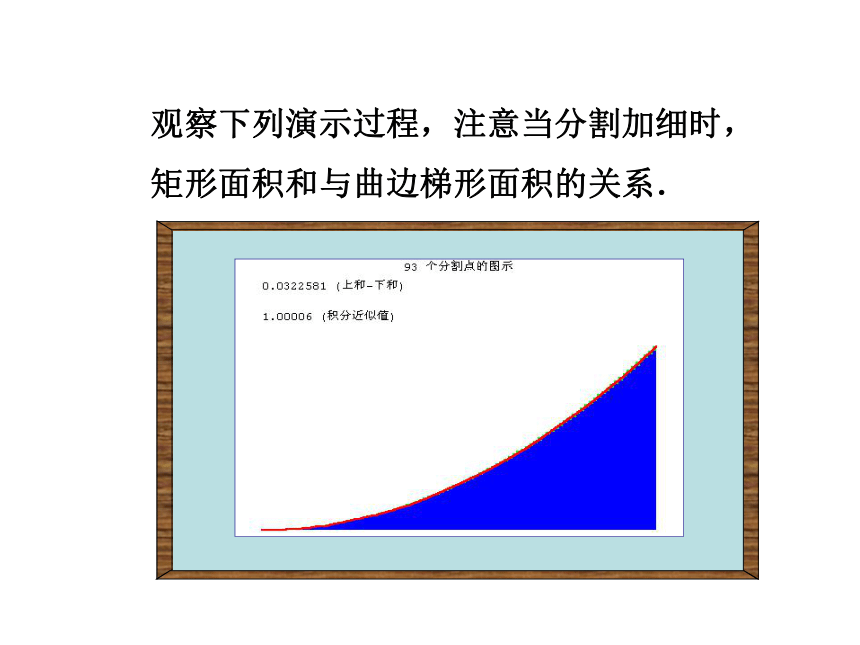
课件31张PPT。1.5.3 定积分的概念观察下列演示过程，注意当分割加细时，
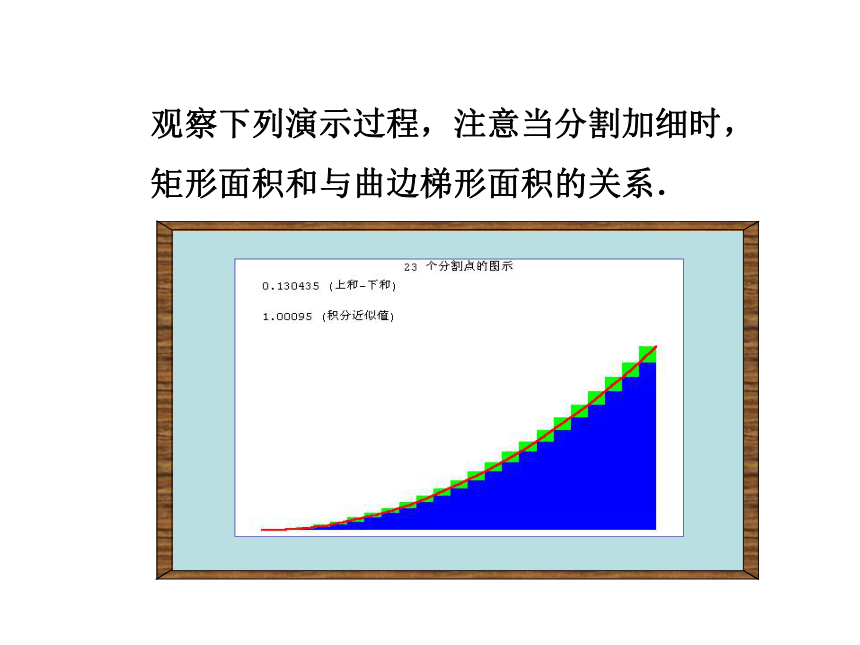
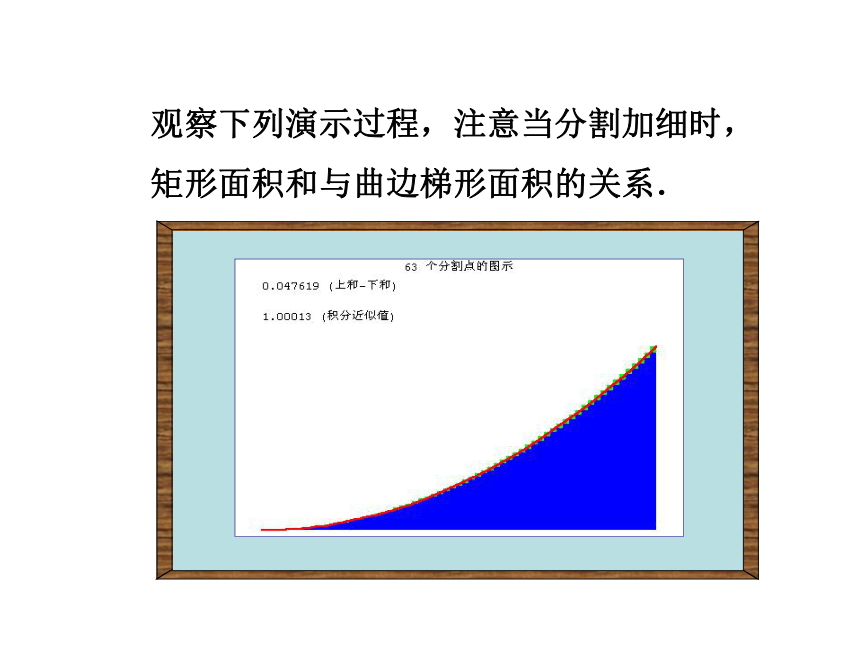
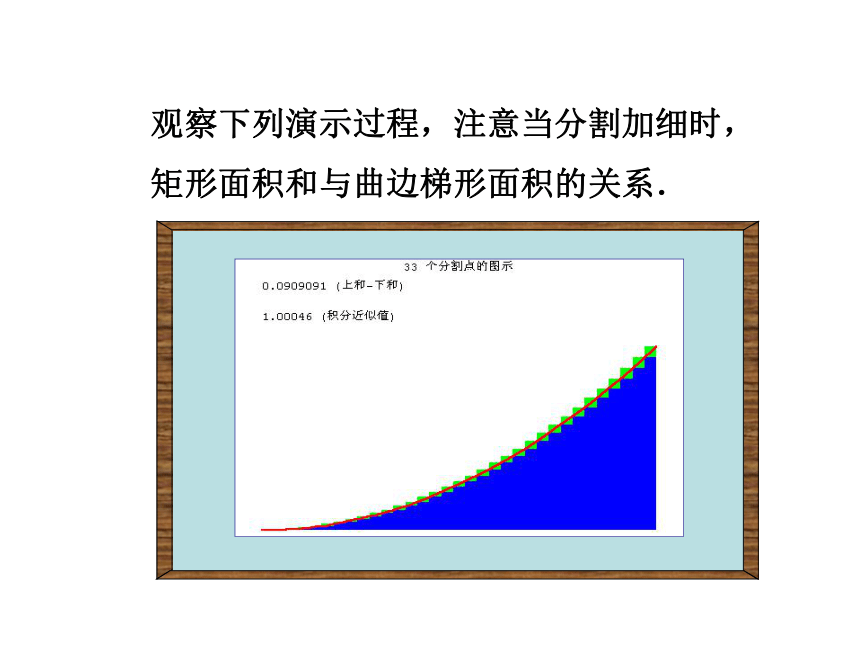
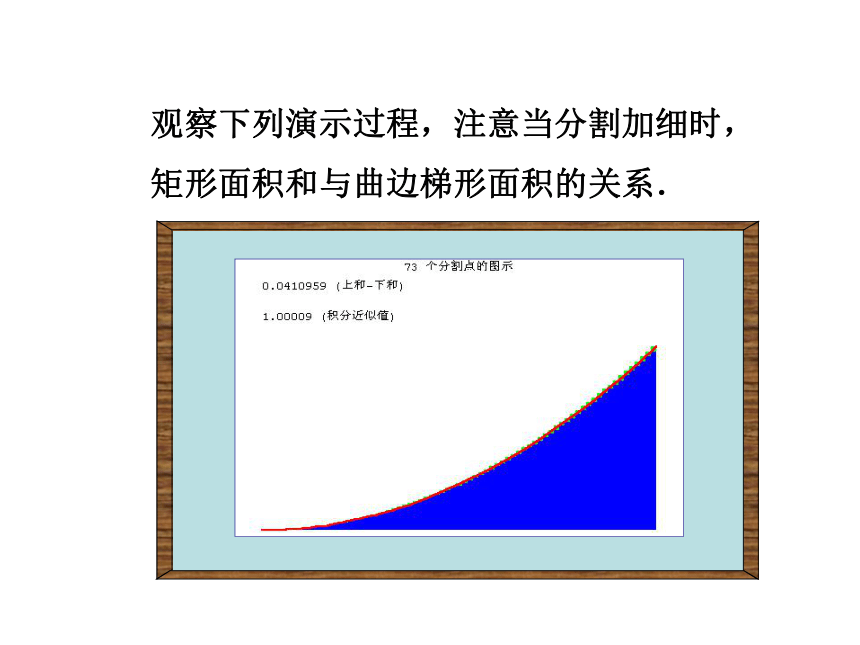
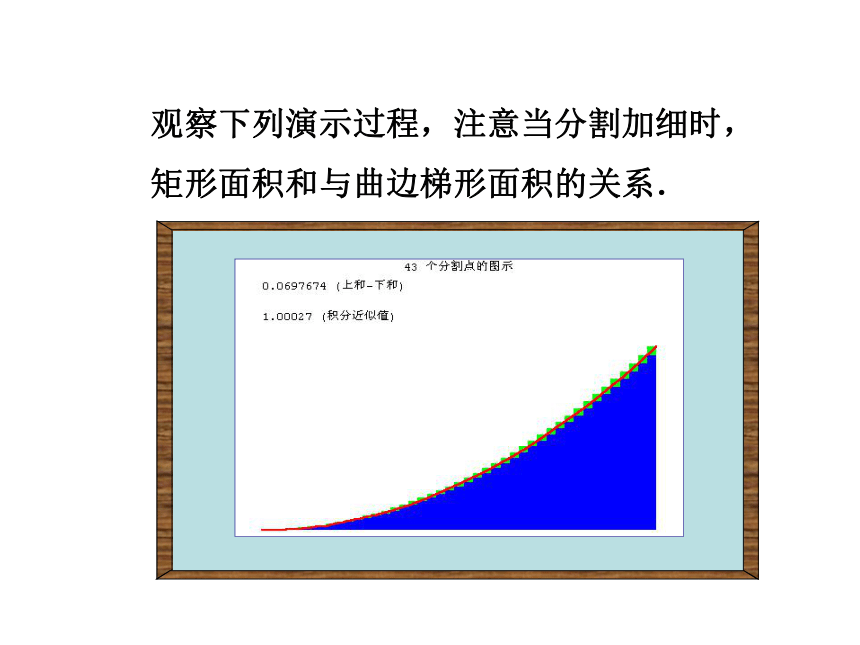
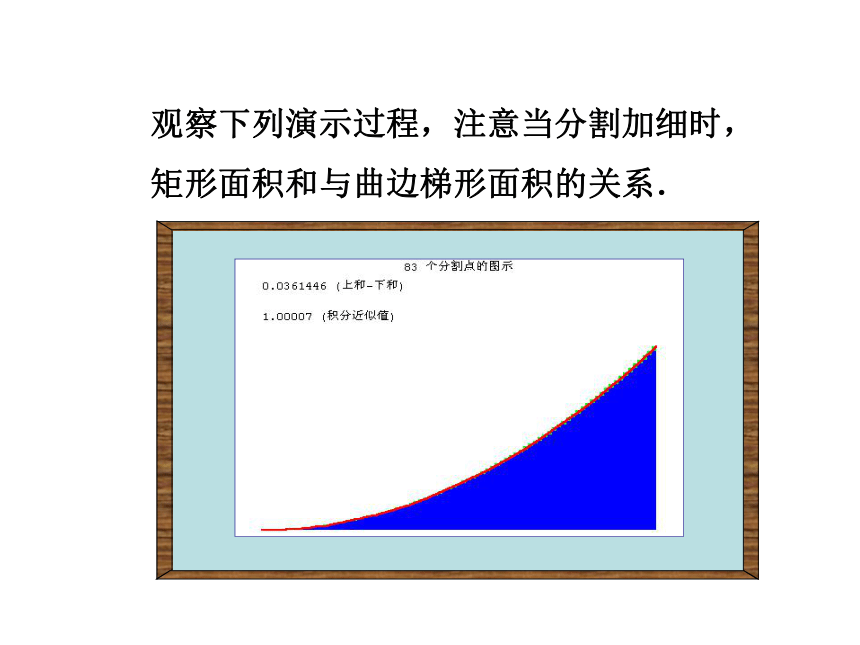
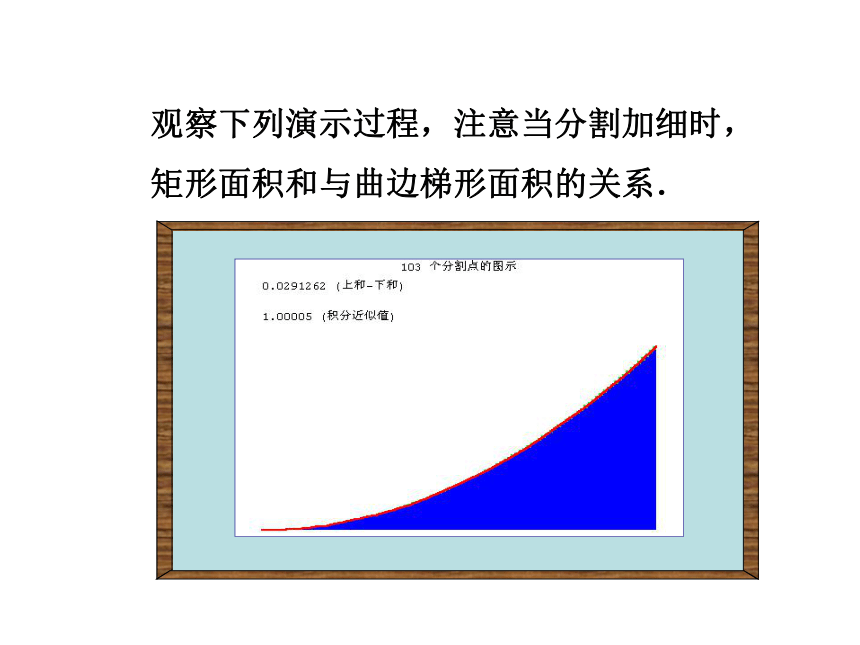
矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，
矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，
矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，
矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，
矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，
矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，
矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，
矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，
矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，
矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，
矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，
矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，
矩形面积和与曲边梯形面积的关系．求由连续曲线y=f(x)对应的曲边梯形面积的方法 (2)取近似求和:任取xi?[xi-1, xi]，第i个小曲边梯形的面积用高为f(xi)而宽为Dx的小矩形面积
f(xi)Dx近似之。 (3)取极限:，所求曲边梯形的面积S为 取n个小矩形面积的和作为曲边梯形面积S的近似值：xixi+1xi一、定积分的定义 如果当n?∞时，S 的无限接近某个常数，这个常数为函数f(x)在区间[a, b]上的定积分，记作从求曲边梯形面积S的过程中可以看出,通过“四步曲”:
分割---近似代替----求和------取极限得到解决.定积分的定义：定积分的相关名称：
? ———叫做积分号，
f(x) ——叫做被积函数，
f(x)dx —叫做被积表达式，
x ———叫做积分变量，
a ———叫做积分下限，
b ———叫做积分上限，
[a, b] —叫做积分区间。积分下限积分上限 按定积分的定义，有
(1) 由连续曲线y=f(x) (f(x)?0) ，直线x=a、x=b及x轴所围成的曲边梯形的面积为 (2) 设物体运动的速度v=v(t)，则此物体在时间区间[a, b]内运动的距离s为定积分的定义：1 说明：
(1) 定积分是一个数值,
它只与被积函数及积分区间有关，
而与积分变量的记法无关，即(2)定积分的几何意义： x=a、x=b与 x轴所围成的曲边梯形的面积。 当f(x)?0时，由y?f (x)、x?a、x?b 与 x 轴所围成的曲边梯形位于 x 轴的下方，上述曲边梯形面积的负值。 定积分的几何意义：探究:
根据定积分的几何意义,如何用定积分表示图中阴影部分的面积?三: 定积分的基本性质 性质1. 性质2. 三: 定积分的基本性质 定积分关于积分区间具有可加性性质3. 性质 3 不论a，b，c的相对位置如何都有 例1：利用定积分的定义,计算
的值.
作业：Ｐ５６Ａ组５（４）Ｂ组２
练习：Ｐ５５-５６Ａ组３，４Ｂ组１，４，３