相交线
图片预览



文档简介
5.1.1 相交线
教学目标
1.通过动手观察、操作、推断、交流等数学活动,进一步发展空间观念,培养识图能力、推理能力和有条理表达能力.毛
2.在具体情境中了解邻补角、对顶角, 能找出图形中的一个角的邻补角和对顶角,理解对顶角相等,并能运用它解决一些问题.
重点、难点
重点:邻补角、对顶角的概念,对顶角性质与应用.
难点:理解对顶角相等的性质的探索.
教学过程
一、自主学习
1.观察剪刀剪布的过程,引入两条相交直线所成的角
小组内表演剪刀剪布过程,观察、思考,得出:
握紧把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角边相应变__. 如果改变用力方向,随着两个把手之间的角逐渐变大,剪刀刃之间的角也相应变__.
如果把剪刀的构造看作两条相交的直线,以上就关系到两条相交直线所成的角的问题,本节课就是探讨两条相交线所成的角及其特征.
2.认识邻补角和对顶角,探索对顶角性质
(1).画直线AB、CD相交于点O,并说出图中4个角。两两相配共能组成几对角 各对角的位置关系如何 根据不同的位置怎么将它们分类 学生思考并在小组内交流.
(2).用量角器分别量一量各个角的度数,以发现各类角的度数有什么关系,学生得出有“相邻”关系的两角互补,“对顶”关系的两角相等.
(3).学生根据观察和度量完成下表:
两直线相交 所形成的角 分类 位置关系 数量关系
如果改变∠AOC的大小, 会改变它与其它角的位置关系和数量关系吗_________________________________________________
3.概括形成邻补角、对顶角概念.
_______________________________叫做邻补角.
__________________________________叫对顶角.
4. ①邻补角的“邻”就是___,就是它们有一条___,“补”就是___,就是这两角的另一条边________.
②邻补角可看成是平角被过它顶点的____分成的___角.
③邻补角是互补的两个角,互补的两个角也是邻补角吗 ________
5.对顶角性质.
(1)在图(1)中,∠AOC的邻补角是__和___,所以∠AOC与___互补,∠AOC 与__互补,根据“同角的补角相等”,可以得出__=___,类似地有___=___.
(2)对顶角性质:______.
(3)对顶角的概念是确定二角的___关系,对顶角性质是确定为对顶角的两角的__关系.
(3)利用对顶角相等这条性质解释剪刀剪布过程中所看到的现象.___________
二、合作探究
(一)、判断题:
1.如果两个角有公共顶点和一条公共边,而且这两角互为补角, 那么它们互为邻补角. ( )
2.两条直线相交,如果它们所成的邻补角相等,那么一对对顶角就互补. ( )
(二)、填空题:
1.如图1,直线AB、CD、EF相交于点O,∠BOE的对顶角是_______,∠COF 的邻补角是________.若∠AOC:∠AOE=2:3,∠EOD=130°,则∠BOC=_________.
(1) (2)
2.如图2,直线AB、CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°, 则∠EOF=________.
三、巩固运用
1.例:如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数.
2.判断下列图中是否存在对顶角.
3.如图,直线AB、CD相交于点O.
(1)若∠AOC+∠BOD=100°,求各角的度数.
(2)若∠BOC比∠AOC的2倍多33°,求各角的度数.毛
4.两条直线相交,如果它们所成的一对对顶角互补, 那么它的所成的各角的度数是多少
5.1.2 垂线(第一课时)
教学目标
1.经历观察、操作、想像、归纳概括、交流等活动,进一步发展空间观念,用几何语言准确表达能力.毛
2.了解垂直概念,能说出垂线的性质“经过一点,能画出已知直线的一条垂线, 并且只能画出一条垂线”,会用三角尺或量角器过一点画一条直线的垂线.
教学重点
两条直线互相垂直的概念、性质和画法.
教学过程
一、自主学习
1.学生观察教室里的课桌面、黑板面相邻的两条边, 方格纸的横线和竖线……,思考这些给大家什么印象 _____________________
2.小组分析讨论:固定木条a,转动木条b, 当b的位置变化时,a、b所成的角a是如何变化的 其中会有特殊情况出现吗 当这种情况出现时,a、b所成的四个角有什么特殊关系
当b的位置变化时,角a从锐角变为___,其中∠a是__角是特殊情况.其特殊之处还在于:当∠a是直角时,它的邻补角,对顶角都是__角,即a、b所成的四个角都是__角,都___.
3.分清“互相垂直”与“垂线”的区别与联系:“互相垂直”指两条直线的___关系;“垂线”是指其中____对_____的命名。 如果说两条直线“互相垂直”时,其中一条必定是另一条的____, 如果一条直线是另一条直线的“垂线”,则它们必定_____。
4.垂直的表示法.
垂直用符号___来表示, “直线AB垂直于直线CD, 垂足为O”,则记为____,垂足为_,并在图中任意一个角处作上直角记号,如图.
5.学生用三角尺或量角器画已知直线L的垂线.
(1)已知直线L,画出直线L的垂线.还能画出L的垂线吗 ___能画几条 ___明确直线L的垂线有无数多条,即存在,但有不确定性.怎样才能确定直线L的垂线位置?在直线L上取一点,过点A画L的垂线.
结论:经过直线上一点_________与已知直线垂直.
(2)经过直线L外一点B画直线L的垂线,这样的垂线能画出__条
结论:经过直线外一点_________与已知直线垂直.
垂线性质1:______________________
二、合作探究
(一)判断以下两条直线是否垂直:
①两条直线相交所成的四个角中有一个是直角;
②两条直线相交所成的四个角相等;
③两条直线相交,有一组邻补角相等;
④两条直线相交,对顶角互补.
(二).变式训练,巩固垂线的概念和画法,如图根据下列语句画图:
(1)过点P画射线MN的垂线,Q为垂足;
(2)过点P画射线BN的垂线,交射线BN反向延长线于Q点;
(3)过点P画线段AB的垂线,交线AB延长线于Q点.
画一条射线或线段的垂线, 就是画它们所在___线的垂线.
(三)、判断题.
1.两条直线互相垂直,则所有的邻补角都相等.( )
2.一条直线不可能与两条相交直线都垂直.( )
3.两条直线相交所成的四个角中,如果有三个角相等,那么这两条直线互为垂直.( )
(四)、填空题.
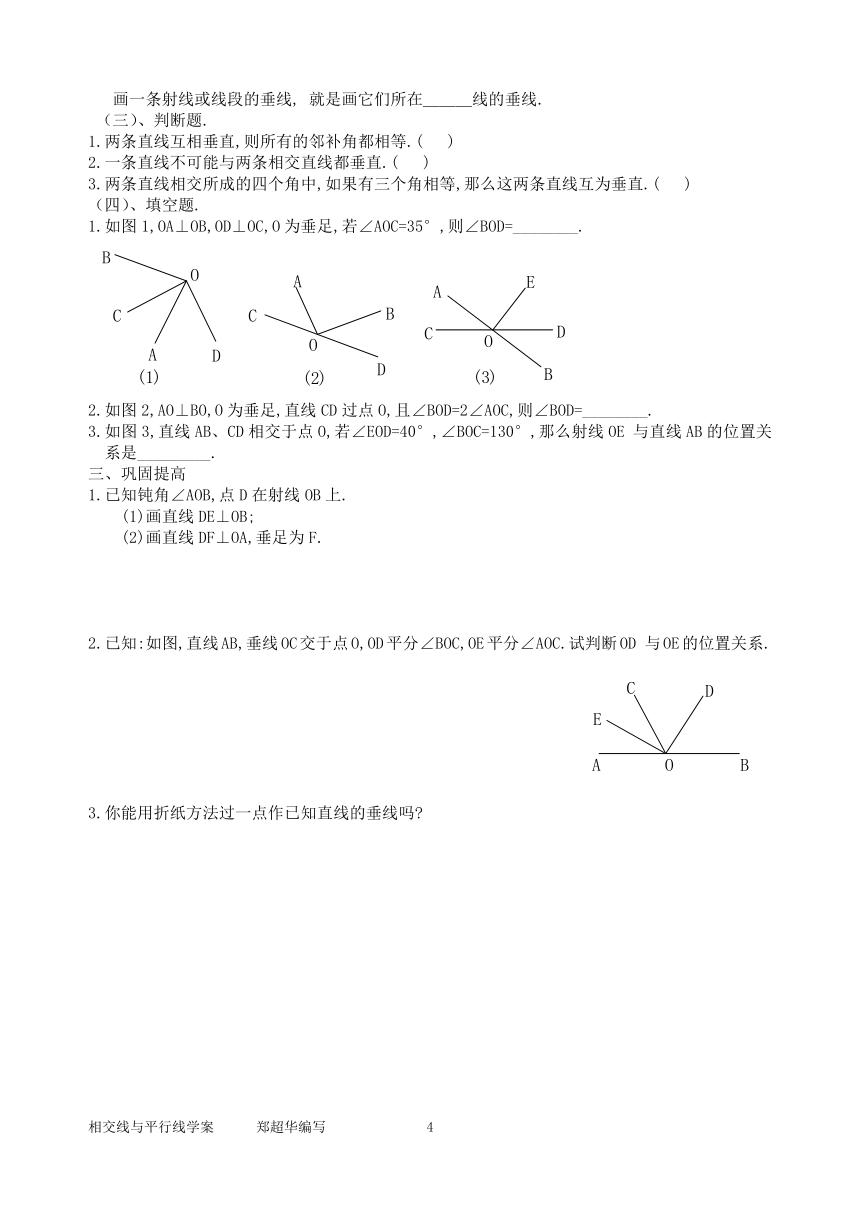
1.如图1,OA⊥OB,OD⊥OC,O为垂足,若∠AOC=35°,则∠BOD=________.
2.如图2,AO⊥BO,O为垂足,直线CD过点O,且∠BOD=2∠AOC,则∠BOD=________.
3.如图3,直线AB、CD相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE 与直线AB的位置关系是_________.
三、巩固提高
1.已知钝角∠AOB,点D在射线OB上.
(1)画直线DE⊥OB;
(2)画直线DF⊥OA,垂足为F.
2.已知:如图,直线AB,垂线OC交于点O,OD平分∠BOC,OE平分∠AOC.试判断OD 与OE的位置关系.
3.你能用折纸方法过一点作已知直线的垂线吗
5.1.2垂线(第2课时)
教学目标
1.经历观察、操作、想像、归纳概括、交流等活动,进一步发展空间观念,用几何语言准确表达能力。毛
2.了解垂线段的概念,了解垂线段最短的性质,体会点到直线的距离的意义, 并会度量点到直线的距离.
重点、难点
重点:“垂线段最短”的性质,点到直线的距离的概念及其简单应用.
难点:对点到直线的距离的概念的理解.
教学过程
一、自主学习
1.观察课本图5.1-8,问题:要把河中的水引到农田P处, 如何挖渠能使渠道最短
(1)问题1,上学期我们曾经学过什么最短的知识,还记得吗 ___________
(2)问题2,如果把渠道看成是线段,它的一个端点自然是P,那么另一个端点的位置呢 ____________________
2.教师演示教具,给学生直观的感受.
教具如图:在硬纸板上固定木条L,L外一点P,转动的木条a一端固定在点P. 使木条L与a相交,左右摆动木条a,L与a的交点A随之变化,线段PA 长度也随之变化.PA最短时,a与L的位置关系如何 _____用三角尺检验.
3.学生画图操作,得出结论.
(1)画出直线L,L外一点P; (2)过P点出PO⊥L,垂足为O;
(3)点A1,A2,A3……在L上,连接PA、PA2、PA3……;
(4)用叠合法或度量法比较PO、PA1、PA2、PA3……长短.
得出垂线的另一条性质.________________________
简单说成:_____________.
4思考:
(1)垂线段与垂线的区别联系.___________________
(2)垂线段与线段的区别与联系.__________________
5.结合课本图形(图5.1-9),深入认识垂线段PO:PO⊥L,∠POA=90°,O为垂足,垂线段PO的长度比其他线段PA1、PA2……中是最短的.得
________________________叫做点到直线的距离.
在图5.1-9中,___的____是点P到直线L的距离,其余结论PA、PA2……长度都不是点P到L的距离.
二、合作探究
1:已知直线a、b,过点a上一点A作AB⊥a,交b于点B,过B作BC⊥b交a 上于点C.请说出哪一条线段的长是哪一点到哪一条直线的距离 并且用刻度尺测量这个距离.
2:课本中水渠该怎么挖 在图上画出来.如果图中比例尺为1:100000, 水渠大约要挖多长
3:判断正确与错误,如果正确,请说明理由,若错误,请订正.
(1)直线外一点与直线上的一点间的线段的长度是这一点到这条直线的距离.
(2)如图,线段AE是点A到直线BC的距离.
(3)如图,线段CD的长是点C到直线AB的距离.
4.如图,AC⊥BC,C为垂足,CD⊥AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6,那么点C到AB的距离是_______,点A到BC的距离是________,点B到CD 的距离是_____,A、B两点的距离是_________.
2.如图,在线段AB、AC、AD、AE、AF中AD最短.小明说垂线段最短, 因此线段AD的长是点A到BF的距离,对小明的说法,你认为_________________.
三、巩固提高
1.(1)用三角尺画一个是30°的∠AOB,在边OA上任取一点P,过P作PQ⊥OB, 垂足为Q,量一量OP的长,你发现点P到OB的距离与OP长的关系吗
(2)若所画的∠AOB为60°角,重复上述的作图和测量,你能发现什么
2.如图,分别画出点A、B、C到BC、AC、AB的垂线段,再量出A到BC、点B到AC、 点C到AB的距离.
同位角内错角同旁内角
[教学目标]
1.能说出同位角、内错角和同旁内角的意义。
2.会识别图形(包括变式图形和比较复杂的图形)中的同位角、内错角和同旁内角。
此外,这种训练过程中,不断提高学生排除变式图形中的非本质现象。复杂图形中“背景”干扰的能力。
一、自主学习
1.复习两条直线相交得到的四个角的位置关系及性质;(口答)
2.展示图形,如图2.3-1。
(1)问题1:如图,怎样描述直线AB、CD和EF的位置关系?_______________________
(2)问题2:如图,直线AB、CD被EF所截得到八个角,这其中有哪些我们已经学过的有特殊位置关系的角?_______________________________
(3)问题3:观察图中的∠1和∠5,它们的位置关系有什么特点?_____________________
像这样位置相同的一对角叫做____角。 图2.3-1
(4)问题4:你还能在图中找出其他的同位角吗?___一共有几对?_____
(5)问题5:你能看出两个同位角的边与边之间有什么关系吗?________
(互为同位角的两个角没有公共顶点和公共边,但有一条边在同一条直线上,然后将上述互为同位角的两个角,从图2.3-1中分解出来,画出如图2.3-2的草图,从这些简单图形中容易识别出∠1和∠2都是同位角。可顺便指出,形如“F”的图形中有同位角。)
图2.3-2
(6)问题6:图2.3-3中的∠1和∠2是同位角吗?为什么?
图2.3-3
(7)问题7:图2.3-1中的∠3和∠5的位置关系是怎样的?∠3和∠5在直线AB、CD___,并且分别在直线EF的___。“像这样的一对角叫做内错角”。其中“错”为“交错”的意思。
(8)问题8:图2.3—l中还有哪些角是内错角?
(9)问题9:你会从图2.3-1中“分解”出这些内错角吗?这些(分解后的内错角)图形像哪一个英文字母?___
(10)说出图2.3-l中的内错角是哪两条直线被哪一条直线截得的。_______
(11)问题10:图2.3-4中的∠1和∠2是内错角吗?为什么?
图2.3-4
(12)问题11:观察图2.3-1中的∠4和∠5有什么位置关系?
∠4和∠5都在直线__、__之间,但它们在直线___的同一侧,像这样的一对角叫______。
(13)问题12:图2.3-1中还有哪些同旁内角?并说出它们是哪两条直线被哪一条直线截得的?______________________________
(14)问题13:图2.3-5中的∠1和∠2是同旁内角吗?为什么?________
二、合作探究:教材第7页例
三、巩固提高:教材第7页练习1、2题
PAGE
8
相交线与平行线学案 郑超华编写
教学目标
1.通过动手观察、操作、推断、交流等数学活动,进一步发展空间观念,培养识图能力、推理能力和有条理表达能力.毛
2.在具体情境中了解邻补角、对顶角, 能找出图形中的一个角的邻补角和对顶角,理解对顶角相等,并能运用它解决一些问题.
重点、难点
重点:邻补角、对顶角的概念,对顶角性质与应用.
难点:理解对顶角相等的性质的探索.
教学过程
一、自主学习
1.观察剪刀剪布的过程,引入两条相交直线所成的角
小组内表演剪刀剪布过程,观察、思考,得出:
握紧把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角边相应变__. 如果改变用力方向,随着两个把手之间的角逐渐变大,剪刀刃之间的角也相应变__.
如果把剪刀的构造看作两条相交的直线,以上就关系到两条相交直线所成的角的问题,本节课就是探讨两条相交线所成的角及其特征.
2.认识邻补角和对顶角,探索对顶角性质
(1).画直线AB、CD相交于点O,并说出图中4个角。两两相配共能组成几对角 各对角的位置关系如何 根据不同的位置怎么将它们分类 学生思考并在小组内交流.
(2).用量角器分别量一量各个角的度数,以发现各类角的度数有什么关系,学生得出有“相邻”关系的两角互补,“对顶”关系的两角相等.
(3).学生根据观察和度量完成下表:
两直线相交 所形成的角 分类 位置关系 数量关系
如果改变∠AOC的大小, 会改变它与其它角的位置关系和数量关系吗_________________________________________________
3.概括形成邻补角、对顶角概念.
_______________________________叫做邻补角.
__________________________________叫对顶角.
4. ①邻补角的“邻”就是___,就是它们有一条___,“补”就是___,就是这两角的另一条边________.
②邻补角可看成是平角被过它顶点的____分成的___角.
③邻补角是互补的两个角,互补的两个角也是邻补角吗 ________
5.对顶角性质.
(1)在图(1)中,∠AOC的邻补角是__和___,所以∠AOC与___互补,∠AOC 与__互补,根据“同角的补角相等”,可以得出__=___,类似地有___=___.
(2)对顶角性质:______.
(3)对顶角的概念是确定二角的___关系,对顶角性质是确定为对顶角的两角的__关系.
(3)利用对顶角相等这条性质解释剪刀剪布过程中所看到的现象.___________
二、合作探究
(一)、判断题:
1.如果两个角有公共顶点和一条公共边,而且这两角互为补角, 那么它们互为邻补角. ( )
2.两条直线相交,如果它们所成的邻补角相等,那么一对对顶角就互补. ( )
(二)、填空题:
1.如图1,直线AB、CD、EF相交于点O,∠BOE的对顶角是_______,∠COF 的邻补角是________.若∠AOC:∠AOE=2:3,∠EOD=130°,则∠BOC=_________.
(1) (2)
2.如图2,直线AB、CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°, 则∠EOF=________.
三、巩固运用
1.例:如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数.
2.判断下列图中是否存在对顶角.
3.如图,直线AB、CD相交于点O.
(1)若∠AOC+∠BOD=100°,求各角的度数.
(2)若∠BOC比∠AOC的2倍多33°,求各角的度数.毛
4.两条直线相交,如果它们所成的一对对顶角互补, 那么它的所成的各角的度数是多少
5.1.2 垂线(第一课时)
教学目标
1.经历观察、操作、想像、归纳概括、交流等活动,进一步发展空间观念,用几何语言准确表达能力.毛
2.了解垂直概念,能说出垂线的性质“经过一点,能画出已知直线的一条垂线, 并且只能画出一条垂线”,会用三角尺或量角器过一点画一条直线的垂线.
教学重点
两条直线互相垂直的概念、性质和画法.
教学过程
一、自主学习
1.学生观察教室里的课桌面、黑板面相邻的两条边, 方格纸的横线和竖线……,思考这些给大家什么印象 _____________________
2.小组分析讨论:固定木条a,转动木条b, 当b的位置变化时,a、b所成的角a是如何变化的 其中会有特殊情况出现吗 当这种情况出现时,a、b所成的四个角有什么特殊关系
当b的位置变化时,角a从锐角变为___,其中∠a是__角是特殊情况.其特殊之处还在于:当∠a是直角时,它的邻补角,对顶角都是__角,即a、b所成的四个角都是__角,都___.
3.分清“互相垂直”与“垂线”的区别与联系:“互相垂直”指两条直线的___关系;“垂线”是指其中____对_____的命名。 如果说两条直线“互相垂直”时,其中一条必定是另一条的____, 如果一条直线是另一条直线的“垂线”,则它们必定_____。
4.垂直的表示法.
垂直用符号___来表示, “直线AB垂直于直线CD, 垂足为O”,则记为____,垂足为_,并在图中任意一个角处作上直角记号,如图.
5.学生用三角尺或量角器画已知直线L的垂线.
(1)已知直线L,画出直线L的垂线.还能画出L的垂线吗 ___能画几条 ___明确直线L的垂线有无数多条,即存在,但有不确定性.怎样才能确定直线L的垂线位置?在直线L上取一点,过点A画L的垂线.
结论:经过直线上一点_________与已知直线垂直.
(2)经过直线L外一点B画直线L的垂线,这样的垂线能画出__条
结论:经过直线外一点_________与已知直线垂直.
垂线性质1:______________________
二、合作探究
(一)判断以下两条直线是否垂直:
①两条直线相交所成的四个角中有一个是直角;
②两条直线相交所成的四个角相等;
③两条直线相交,有一组邻补角相等;
④两条直线相交,对顶角互补.
(二).变式训练,巩固垂线的概念和画法,如图根据下列语句画图:
(1)过点P画射线MN的垂线,Q为垂足;
(2)过点P画射线BN的垂线,交射线BN反向延长线于Q点;
(3)过点P画线段AB的垂线,交线AB延长线于Q点.
画一条射线或线段的垂线, 就是画它们所在___线的垂线.
(三)、判断题.
1.两条直线互相垂直,则所有的邻补角都相等.( )
2.一条直线不可能与两条相交直线都垂直.( )
3.两条直线相交所成的四个角中,如果有三个角相等,那么这两条直线互为垂直.( )
(四)、填空题.
1.如图1,OA⊥OB,OD⊥OC,O为垂足,若∠AOC=35°,则∠BOD=________.
2.如图2,AO⊥BO,O为垂足,直线CD过点O,且∠BOD=2∠AOC,则∠BOD=________.
3.如图3,直线AB、CD相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE 与直线AB的位置关系是_________.
三、巩固提高
1.已知钝角∠AOB,点D在射线OB上.
(1)画直线DE⊥OB;
(2)画直线DF⊥OA,垂足为F.
2.已知:如图,直线AB,垂线OC交于点O,OD平分∠BOC,OE平分∠AOC.试判断OD 与OE的位置关系.
3.你能用折纸方法过一点作已知直线的垂线吗
5.1.2垂线(第2课时)
教学目标
1.经历观察、操作、想像、归纳概括、交流等活动,进一步发展空间观念,用几何语言准确表达能力。毛
2.了解垂线段的概念,了解垂线段最短的性质,体会点到直线的距离的意义, 并会度量点到直线的距离.
重点、难点
重点:“垂线段最短”的性质,点到直线的距离的概念及其简单应用.
难点:对点到直线的距离的概念的理解.
教学过程
一、自主学习
1.观察课本图5.1-8,问题:要把河中的水引到农田P处, 如何挖渠能使渠道最短
(1)问题1,上学期我们曾经学过什么最短的知识,还记得吗 ___________
(2)问题2,如果把渠道看成是线段,它的一个端点自然是P,那么另一个端点的位置呢 ____________________
2.教师演示教具,给学生直观的感受.
教具如图:在硬纸板上固定木条L,L外一点P,转动的木条a一端固定在点P. 使木条L与a相交,左右摆动木条a,L与a的交点A随之变化,线段PA 长度也随之变化.PA最短时,a与L的位置关系如何 _____用三角尺检验.
3.学生画图操作,得出结论.
(1)画出直线L,L外一点P; (2)过P点出PO⊥L,垂足为O;
(3)点A1,A2,A3……在L上,连接PA、PA2、PA3……;
(4)用叠合法或度量法比较PO、PA1、PA2、PA3……长短.
得出垂线的另一条性质.________________________
简单说成:_____________.
4思考:
(1)垂线段与垂线的区别联系.___________________
(2)垂线段与线段的区别与联系.__________________
5.结合课本图形(图5.1-9),深入认识垂线段PO:PO⊥L,∠POA=90°,O为垂足,垂线段PO的长度比其他线段PA1、PA2……中是最短的.得
________________________叫做点到直线的距离.
在图5.1-9中,___的____是点P到直线L的距离,其余结论PA、PA2……长度都不是点P到L的距离.
二、合作探究
1:已知直线a、b,过点a上一点A作AB⊥a,交b于点B,过B作BC⊥b交a 上于点C.请说出哪一条线段的长是哪一点到哪一条直线的距离 并且用刻度尺测量这个距离.
2:课本中水渠该怎么挖 在图上画出来.如果图中比例尺为1:100000, 水渠大约要挖多长
3:判断正确与错误,如果正确,请说明理由,若错误,请订正.
(1)直线外一点与直线上的一点间的线段的长度是这一点到这条直线的距离.
(2)如图,线段AE是点A到直线BC的距离.
(3)如图,线段CD的长是点C到直线AB的距离.
4.如图,AC⊥BC,C为垂足,CD⊥AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6,那么点C到AB的距离是_______,点A到BC的距离是________,点B到CD 的距离是_____,A、B两点的距离是_________.
2.如图,在线段AB、AC、AD、AE、AF中AD最短.小明说垂线段最短, 因此线段AD的长是点A到BF的距离,对小明的说法,你认为_________________.
三、巩固提高
1.(1)用三角尺画一个是30°的∠AOB,在边OA上任取一点P,过P作PQ⊥OB, 垂足为Q,量一量OP的长,你发现点P到OB的距离与OP长的关系吗
(2)若所画的∠AOB为60°角,重复上述的作图和测量,你能发现什么
2.如图,分别画出点A、B、C到BC、AC、AB的垂线段,再量出A到BC、点B到AC、 点C到AB的距离.
同位角内错角同旁内角
[教学目标]
1.能说出同位角、内错角和同旁内角的意义。
2.会识别图形(包括变式图形和比较复杂的图形)中的同位角、内错角和同旁内角。
此外,这种训练过程中,不断提高学生排除变式图形中的非本质现象。复杂图形中“背景”干扰的能力。
一、自主学习
1.复习两条直线相交得到的四个角的位置关系及性质;(口答)
2.展示图形,如图2.3-1。
(1)问题1:如图,怎样描述直线AB、CD和EF的位置关系?_______________________
(2)问题2:如图,直线AB、CD被EF所截得到八个角,这其中有哪些我们已经学过的有特殊位置关系的角?_______________________________
(3)问题3:观察图中的∠1和∠5,它们的位置关系有什么特点?_____________________
像这样位置相同的一对角叫做____角。 图2.3-1
(4)问题4:你还能在图中找出其他的同位角吗?___一共有几对?_____
(5)问题5:你能看出两个同位角的边与边之间有什么关系吗?________
(互为同位角的两个角没有公共顶点和公共边,但有一条边在同一条直线上,然后将上述互为同位角的两个角,从图2.3-1中分解出来,画出如图2.3-2的草图,从这些简单图形中容易识别出∠1和∠2都是同位角。可顺便指出,形如“F”的图形中有同位角。)
图2.3-2
(6)问题6:图2.3-3中的∠1和∠2是同位角吗?为什么?
图2.3-3
(7)问题7:图2.3-1中的∠3和∠5的位置关系是怎样的?∠3和∠5在直线AB、CD___,并且分别在直线EF的___。“像这样的一对角叫做内错角”。其中“错”为“交错”的意思。
(8)问题8:图2.3—l中还有哪些角是内错角?
(9)问题9:你会从图2.3-1中“分解”出这些内错角吗?这些(分解后的内错角)图形像哪一个英文字母?___
(10)说出图2.3-l中的内错角是哪两条直线被哪一条直线截得的。_______
(11)问题10:图2.3-4中的∠1和∠2是内错角吗?为什么?
图2.3-4
(12)问题11:观察图2.3-1中的∠4和∠5有什么位置关系?
∠4和∠5都在直线__、__之间,但它们在直线___的同一侧,像这样的一对角叫______。
(13)问题12:图2.3-1中还有哪些同旁内角?并说出它们是哪两条直线被哪一条直线截得的?______________________________
(14)问题13:图2.3-5中的∠1和∠2是同旁内角吗?为什么?________
二、合作探究:教材第7页例
三、巩固提高:教材第7页练习1、2题
PAGE
8
相交线与平行线学案 郑超华编写
