相似三角形的判定(1)`
文档属性
| 名称 | 相似三角形的判定(1)` |  | |
| 格式 | rar | ||
| 文件大小 | 358.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-10 20:39:00 | ||
图片预览






文档简介
课件25张PPT。27.2.1 相似三角形的判定(1)
教学目标:
1、经历三角形相似的判定方法“预备定理”的探索过程.
2、掌握“预备定理” 证明两个三角形相似的判定方法.
教学重点:
相似三角形的判定方法“预备定理” 及其应用.
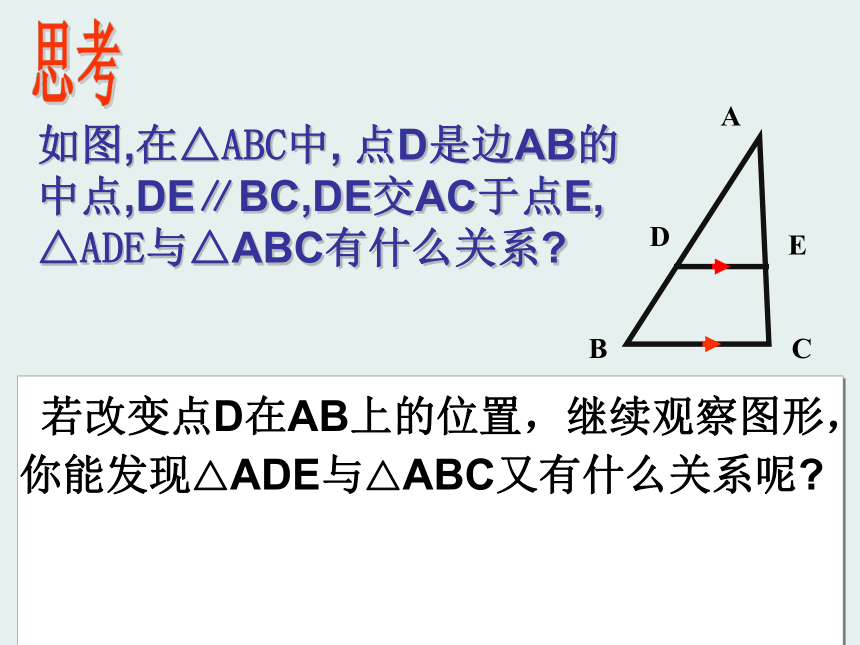
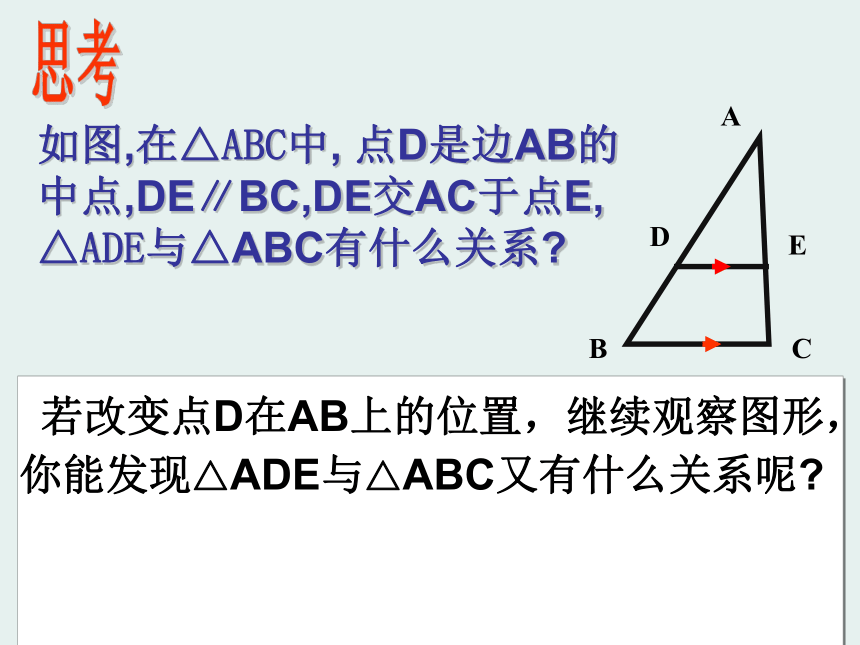
教学重点: 根据计算结果来判断两个三角形的三边是否对应成比例,需要学生有一定的分析、判断和计算能力,是本节教学的难点.一、复习引入。1、相似三角形的定义是什么? 如果那么ΔABC∽ΔA/B/C/ 2、相似三角形与全等三角形有什么内在的联系呢? 全等三角形是相似比为1的特殊的相似三角形。 如图,在△ABC中, 点D是边AB的中点,DE∥BC,DE交AC于点E, △ADE与△ABC有什么关系? 思考 若改变点D在AB上的位置,继续观察图形,你能发现△ADE与△ABC又有什么关系呢?
平行线分线段成比例定理:
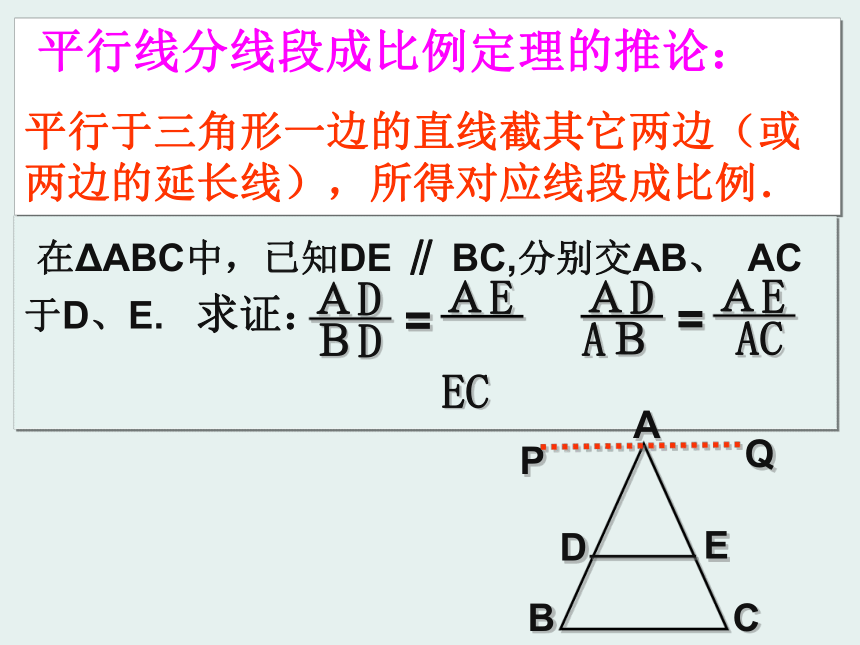
三条平行线截两条直线,所得的对应线段成比例. 平行线分线段成比例定理的推论:
平行于三角形一边的直线截其它两边(或两边的延长线),所得对应线段成比例. 在ΔABC中,已知DE ∥ BC,分别交AB、 AC于D、E. 求证:
如图,在△ABC中, 点D是边AB的中点,DE∥BC,DE交AC于点E, △ADE与△ABC有什么关系? 思考 若改变点D在AB上的位置,继续观察图形,你能发现△ADE与△ABC又有什么关系呢?
1、如果△ABC与△A'B'C'三边对应成比例,那么它们相似吗?探 索三边对应成比例的两个三角形相似。
结 论量一量它们的三对角相等吗? 2。 两边对应成比例且夹角相等的两个三角形相似吗? 两边对应成比例且夹角相等的两个三角形相似.结 论请同学们画两个这样的三角形
并量一量看是否符合相似的条件? 上述判定方法中的“角”一定是两对应边的夹角吗?50°)4AB21.650°)看看演示你有疑问吗 ?3.23.2返回4页7 下面每组的两个三角形是否相似? 请说说你的理由:CACB45⑴⑵ 你会做了吗?运用: 如图,△ABC与△ A’ B’ C’ 相似吗?你有哪些判断方法?再看看你的能力 例1.判断图中△AEB和△FEC是否相似?解 ∵∠AEB=∠FEC(对顶角相等),
= =1.5(已知)
= =1.5(已知)
=
∴ △AEB∽△FEC(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.) 例2.下列每个图形中,是否存在相似三角形?若存在,用字母表示出来,并写出对应的比例式。 有一池塘, 周围都是空地. 如果要测量池塘两端A、B间的距离, 你能利用本节所学的知识解决这个问题吗???AB学 以 致 用★ 探讨了相似三角形的另两种判定方法:★ 数学活动充满着探索与创新,请同学们利用所学知识解决生活中的实际问题. 说说你的 收 获 !想一想 你能用所学的知识说说这样做的理由吗?ABCDF
教学目标:
1、经历三角形相似的判定方法“预备定理”的探索过程.
2、掌握“预备定理” 证明两个三角形相似的判定方法.
教学重点:
相似三角形的判定方法“预备定理” 及其应用.
教学重点: 根据计算结果来判断两个三角形的三边是否对应成比例,需要学生有一定的分析、判断和计算能力,是本节教学的难点.一、复习引入。1、相似三角形的定义是什么? 如果那么ΔABC∽ΔA/B/C/ 2、相似三角形与全等三角形有什么内在的联系呢? 全等三角形是相似比为1的特殊的相似三角形。 如图,在△ABC中, 点D是边AB的中点,DE∥BC,DE交AC于点E, △ADE与△ABC有什么关系? 思考 若改变点D在AB上的位置,继续观察图形,你能发现△ADE与△ABC又有什么关系呢?
平行线分线段成比例定理:
三条平行线截两条直线,所得的对应线段成比例. 平行线分线段成比例定理的推论:
平行于三角形一边的直线截其它两边(或两边的延长线),所得对应线段成比例. 在ΔABC中,已知DE ∥ BC,分别交AB、 AC于D、E. 求证:
如图,在△ABC中, 点D是边AB的中点,DE∥BC,DE交AC于点E, △ADE与△ABC有什么关系? 思考 若改变点D在AB上的位置,继续观察图形,你能发现△ADE与△ABC又有什么关系呢?
1、如果△ABC与△A'B'C'三边对应成比例,那么它们相似吗?探 索三边对应成比例的两个三角形相似。
结 论量一量它们的三对角相等吗? 2。 两边对应成比例且夹角相等的两个三角形相似吗? 两边对应成比例且夹角相等的两个三角形相似.结 论请同学们画两个这样的三角形
并量一量看是否符合相似的条件? 上述判定方法中的“角”一定是两对应边的夹角吗?50°)4AB21.650°)看看演示你有疑问吗 ?3.23.2返回4页7 下面每组的两个三角形是否相似? 请说说你的理由:CACB45⑴⑵ 你会做了吗?运用: 如图,△ABC与△ A’ B’ C’ 相似吗?你有哪些判断方法?再看看你的能力 例1.判断图中△AEB和△FEC是否相似?解 ∵∠AEB=∠FEC(对顶角相等),
= =1.5(已知)
= =1.5(已知)
=
∴ △AEB∽△FEC(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.) 例2.下列每个图形中,是否存在相似三角形?若存在,用字母表示出来,并写出对应的比例式。 有一池塘, 周围都是空地. 如果要测量池塘两端A、B间的距离, 你能利用本节所学的知识解决这个问题吗???AB学 以 致 用★ 探讨了相似三角形的另两种判定方法:★ 数学活动充满着探索与创新,请同学们利用所学知识解决生活中的实际问题. 说说你的 收 获 !想一想 你能用所学的知识说说这样做的理由吗?ABCDF
