第四章 基本平面图形(测能力)(含解析)——2023-2024学年北师大版数学七年级上册单元闯关双测卷
文档属性
| 名称 | 第四章 基本平面图形(测能力)(含解析)——2023-2024学年北师大版数学七年级上册单元闯关双测卷 |

|
|
| 格式 | docx | ||
| 文件大小 | 790.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 00:00:00 | ||
图片预览




文档简介
第四章 基本平面图形(测能力)——2023-2024学年北师大版数学七年级上册单元闯关双测卷
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.木兰溪是莆田的母亲河,过去水患频繁.1999年,时任福建省委副书记、代省长的习近平同志参与木兰溪水患治理工作,通过把河道裁弯取直解决了行洪不畅问题.如图,把弯曲的河道改直,还能够缩短航程,根据的道理是( )
A.两点之间,直线最短 B.两点确定一条直线
C.两点之间,线段最短 D.两点确定一条线段
2.若是锐角,是钝角,则计算的结果可能是( )
A. B. C. D.
3.如图,A、B、C是同一平面内不在同一直线上的三点画射线、射线和射线.按上述要求作图后的图形中小于平角的角有( )
A.4个 B.5个 C.6个 D.7个
4.下列语句中:正确的个数有( )
① 画直线;
② 连接点A与点B的线段,叫做A、B两点之间的距离;
③ 两条射线组成的图形叫角;
④ 任何一个有理数都可以用数轴上的一个点来表示.
A.0 B.1 C.2 D.3
5.下列说法正确的是( )
A.各边相等的多边形是正多边形
B.若,则点C是线段的中点
C.顶点在圆上的角叫做圆心角
D.钟表显示9点30分,此时时针与分针的夹角是105°
6.如图,点C是AB的中点,点D是BC的中点,则下列等式中成立的有( )
①;
②;
③;
④
A.①② B.②③ C.①③ D.②④
7.如图,已知,,OM平分,ON平分,则的度数为( )
A.45° B.50° C.55° D.60°
8.已知点M是线段AB上一点,若,点N是直线AB上的一动点,且,则的( )
A. B. C.1或 D.或2
9.如图,O是直线AB上一点,OD平分,,若,则为( )
A.15° B.20° C.30° D.45°
10.定义:从的顶点出发,在角的内部引一条射线,把分成的两部分,射线叫做的三等分线.若在中,射线是的三等分线,射线是的三等分线,设,则用含x的代数式表示为( )
A.或或 B.或或
C.或或 D.或或
二、填空题(每小题4分,共20分)
11.计算:__________;__________°;当时钟指向时间为时,钟表上的时针与分针的夹角为__________度.
12.如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,,若,则AC等于_________.
13.如图,,,OE平分,则_________.
14.如图,已知A,B,C三点在一条直线上.
(1)若点D在线段AB上,则__________;
(2)已知,,若点D在直线AB上,且,则__________.
15.我们把有公共顶点和一条公共边的两个角称为“共边角”.
(1)当两个“共边角”为和时,它们非公共边的两边的夹角为__________°;
(2)若两个“共边角”非公共边的两边所成的角是直角,则这两个角的平分线的夹角度数为__________°.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,
(1)用不同的方法表示图中以D为顶点的角;
(2)写出以B为顶点的角与边;
(3)画出,使成平角,写出它的边.
17.(8分)如图,已知线段,,点M是AC的中点.
(1)求线段AM的长;
(2)在CB上取一点N,使得,求线段MN的长.
18.(10分)探究归纳题:
(1)试验分析:
如图1,经过一个顶点(如点A)可以作___________条对角线,它把四边形分为_________个三角形;
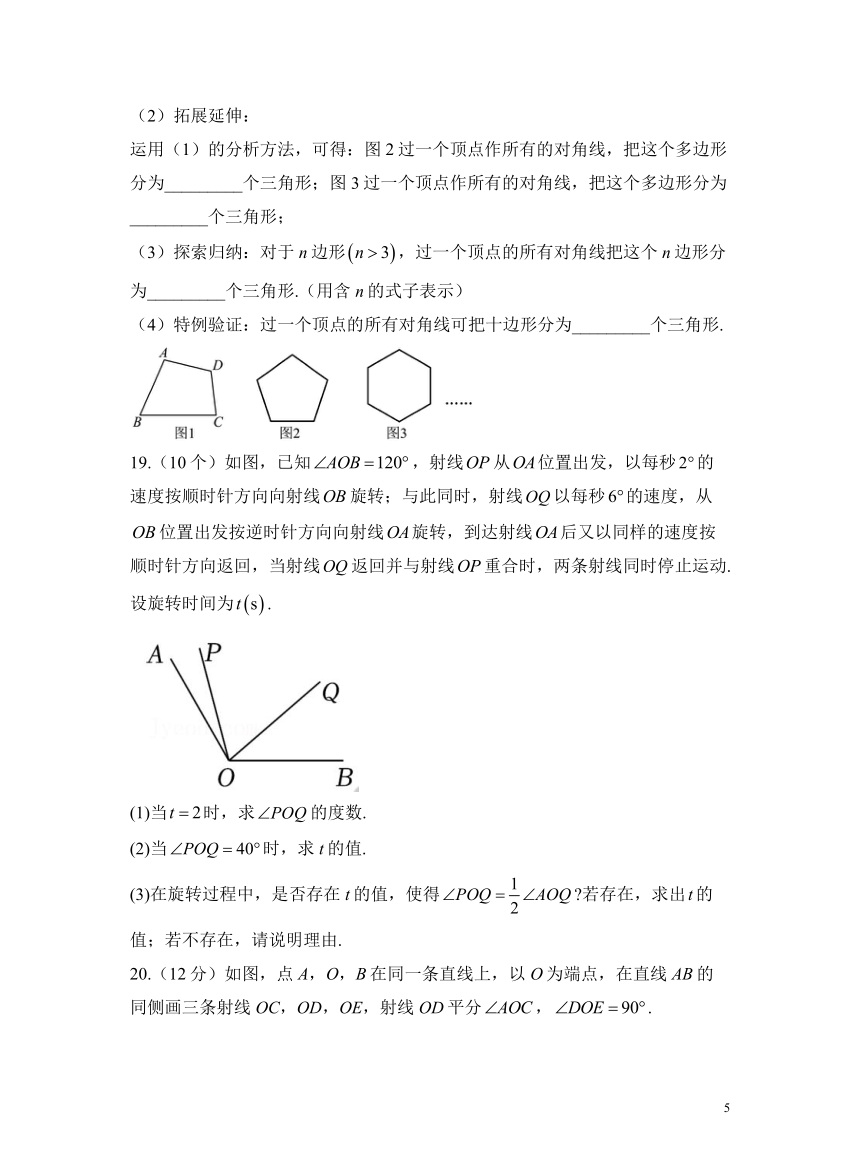
(2)拓展延伸:
运用(1)的分析方法,可得:图2过一个顶点作所有的对角线,把这个多边形分为_________个三角形;图3过一个顶点作所有的对角线,把这个多边形分为_________个三角形;
(3)探索归纳:对于n边形,过一个顶点的所有对角线把这个n边形分为_________个三角形.(用含n的式子表示)
(4)特例验证:过一个顶点的所有对角线可把十边形分为_________个三角形.
19.(10个)如图,已知,射线从位置出发,以每秒的速度按顺时针方向向射线旋转;与此同时,射线以每秒的速度,从位置出发按逆时针方向向射线旋转,到达射线后又以同样的速度按顺时针方向返回,当射线返回并与射线重合时,两条射线同时停止运动.设旋转时间为.
(1)当时,求的度数.
(2)当时,求t的值.
(3)在旋转过程中,是否存在t的值,使得 若存在,求出的值;若不存在,请说明理由.
20.(12分)如图,点A,O,B在同一条直线上,以O为端点,在直线AB的同侧画三条射线OC,OD,OE,射线OD平分,.
(1)射线OE平分吗?为什么?
(2)若,求的度数.
21.(12分)已知,射线BD在的内部,按要求完成下列各小题.
尝试探究:如图1,已知,当BD是的平分线时,的度数为________;
初步应用:如图2,已知,若BD不是的平分线,求的度数;
拓展提升:如图3,若时,试判断与之间的数量关系,并说明理由.
答案以及解析
1.答案:C
解析:因为两点之间线段最短,把弯曲的河道改直,能够缩短航程.故选C.
2.答案:B
解析:由题意可知,
,
,
,
,故选B.
3.答案:C
解析:作图如下:
由图可知:图形中小于平角的角有6个.
故选:C.
4.答案:B
解析:① 直线不可以度量,所以画直线是错误的;
②连接点A与点B的线段的长度,叫做A、B两点之间的距离,原说法错误;
③具有公共端点的两条射线组成的图形叫角,原说法错误;
④任何一个有理数都可以用数轴上的点来表示,原说法正确;
故正确答案有1个.
故选:B.
5.答案:D
解析:A.各边相等,各角都相等的多边形是正多边形,故选项错误,不符合题意;
B.若,点C不一定在线段AB上,故选项错误,不符合题意;
C.顶点在圆心,两条边与圆有交点所形成的角叫做圆心角,故选项错误,不符合题意;
D.钟表显示9点30分,此时时针与分针的夹角是105°,故选项正确,符合题意.
故选:D.
6.答案:B
解析:由图形可得,
,而与不一定相等,
不一定等于,
故①错误,不符合题意;
点C是AB的中点,
,
,
,
故②正确,符合题意;
点D是BC的中点,
,
,
故③正确,符合题意;
,
故④错误,不符合题意,
综上所述,成立的有:②③.
故选:B.
7.答案:B
解析:OM平分,ON平分,
,
,
,
,
即,
,
,
则,
故选:B.
8.答案:C
解析:当N在射线BA上时,,不合题意
当N在射线AB上时,,此时,
当N在线段AB上时,
由图可知,,
,
,
,
,
,
,
故选:C.
9.答案:B
解析:O是直线AB上一点,
,
,
,
平分,
,
,,
.
故选:B.
10.答案:C
解析:如图:射线是的三等分线,射线是的三等分线,
则,,
;
如图:射线是的三等分线,射线是的三等分线,
则,,
;
如图:射线是的三等分线,射线是的三等分线,
则,,
;
如图:射线是的三等分线,射线是的三等分线,
则,,
;
综上,为或或,
故选:C.
11.答案:;;
解析:①,
故答案为:;
②,
,
,
,
故答案为:;
③当时钟指向时间为时,时针走过小时,分钟走过分钟,
时针与0点的夹角为,
分针与0点的夹角为,
钟表上的时针与分针的夹角为,
故答案为:.
12.答案:8
解析:D,B,E三点依次在线段AC上,
,
,,
,.
点B为线段AC的中点,
.
13.答案:110°
解析:因为OE平分,所以.设.因为,所以,所以,所以.故答案为110°.
14.答案:(1)AD
(2)1或3
解析:(1)点D在线段AB上,如图:
,
故答案为:AD;
(2),,且,
当点D在线段AB上,如图:
;
当点D在线段BC上,如图:
;
故答案为:1或3.
15.答案:(1)30或90
(2)45或135
解析:(1)如图1,,,
则;
如图2,,,
则;
故答案为:30或90;
(2),分别是,的平分线,,
如图3,
,分别是,的平分线,
,,
,
,
;
如图4,
,分别是,的平分线,
,,
,
,
;
故答案为:45或135.
16.答案:(1)或或
(2)角为(或或),边是,
(3)图见解析,边是,
解析:(1)由图可得:
用三个字母表示以D为顶点的角为:,
用一个字母表示以D为顶点的角为:,
用数字表示以D为顶点的角为:,
故答案为:或或.
(2)由图可得:
用三个字母表示以B为顶点的角为:,
用一个字母表示以B为顶点的角为:,
用数字表示以B为顶点的角为:,
以B为顶点边是,,
故答案为:角为(或或),边是,.
(3)如图,是射线的反向延长线,
则成平角,的边是,.
17.答案:(1)4
(2)9
解析:(1)线段,,
,
又点M是AC的中点,
,即线段AM的长度是4;
(2),,
,
又点M是AC的中点,,
,
,即MN的长度是9.
18.答案:(1)1,2
(2)3,4
(3)
(4)8
解析:(1)如下图:
经过A点可以做1条对角线,它把四边形分为2个三角形,
故答案为:1,2;
(2)拓展延伸:
运用(1)的分析方法,可得:
图2过一个顶点,共有2条对角线,将这个多边形分为3个三角形;
图3过一个顶点,共有3条对角线,将这个多边形分为4个三角形;
故答案为:3,4;
(3)对于n边形,过一个顶点的所有对角线把这个n边形分为个三角形,
故答案为:;
(4)过一个顶点的所有对角线可把十边形分为个三角形,
故答案为:8.
19.答案:(1)
(2)当时,t的值为10或20
(3)存在或或,使得
解析:(1)当时,,,
(2)与相遇时间为(秒),
与重合时间为(秒),
与停止运动的时间为(秒),
①当时,
根据题意,得,
解得;
②当时,
根据题意,得,
解得;
③当时,
根据题意,得,
解得(不合题意,舍去)
综上所述,当时,t的值为10或20;
(3)①当时,
根据题意,得,
解得;
②当时,
根据题意,得,
解得;
③当时,
根据题意,得,
解得.
综上所述,存在或或,使得.
20.答案:(1)射线OE平分,理由见解析
(2)
解析:(1)设,
因为射线OD平分,
所以,
因为,
所以
因为点A,O,B在同一条直线上,
所以,
所以,
所以,
所以,
所以射线OE平分;
(2)因为,由(1)知,
所以,
解得,
所以.
21.答案:
解析:尝试探究:,BD平分,
所以,
因为,
所以.
所以.
初步应用:因为,
所以.
答:的度数为.
拓展提升:.
理由:因为,
所以.
1
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.木兰溪是莆田的母亲河,过去水患频繁.1999年,时任福建省委副书记、代省长的习近平同志参与木兰溪水患治理工作,通过把河道裁弯取直解决了行洪不畅问题.如图,把弯曲的河道改直,还能够缩短航程,根据的道理是( )
A.两点之间,直线最短 B.两点确定一条直线
C.两点之间,线段最短 D.两点确定一条线段
2.若是锐角,是钝角,则计算的结果可能是( )
A. B. C. D.
3.如图,A、B、C是同一平面内不在同一直线上的三点画射线、射线和射线.按上述要求作图后的图形中小于平角的角有( )
A.4个 B.5个 C.6个 D.7个
4.下列语句中:正确的个数有( )
① 画直线;
② 连接点A与点B的线段,叫做A、B两点之间的距离;
③ 两条射线组成的图形叫角;
④ 任何一个有理数都可以用数轴上的一个点来表示.
A.0 B.1 C.2 D.3
5.下列说法正确的是( )
A.各边相等的多边形是正多边形
B.若,则点C是线段的中点
C.顶点在圆上的角叫做圆心角
D.钟表显示9点30分,此时时针与分针的夹角是105°
6.如图,点C是AB的中点,点D是BC的中点,则下列等式中成立的有( )
①;
②;
③;
④
A.①② B.②③ C.①③ D.②④
7.如图,已知,,OM平分,ON平分,则的度数为( )
A.45° B.50° C.55° D.60°
8.已知点M是线段AB上一点,若,点N是直线AB上的一动点,且,则的( )
A. B. C.1或 D.或2
9.如图,O是直线AB上一点,OD平分,,若,则为( )
A.15° B.20° C.30° D.45°
10.定义:从的顶点出发,在角的内部引一条射线,把分成的两部分,射线叫做的三等分线.若在中,射线是的三等分线,射线是的三等分线,设,则用含x的代数式表示为( )
A.或或 B.或或
C.或或 D.或或
二、填空题(每小题4分,共20分)
11.计算:__________;__________°;当时钟指向时间为时,钟表上的时针与分针的夹角为__________度.
12.如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,,若,则AC等于_________.
13.如图,,,OE平分,则_________.
14.如图,已知A,B,C三点在一条直线上.
(1)若点D在线段AB上,则__________;
(2)已知,,若点D在直线AB上,且,则__________.
15.我们把有公共顶点和一条公共边的两个角称为“共边角”.
(1)当两个“共边角”为和时,它们非公共边的两边的夹角为__________°;
(2)若两个“共边角”非公共边的两边所成的角是直角,则这两个角的平分线的夹角度数为__________°.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,
(1)用不同的方法表示图中以D为顶点的角;
(2)写出以B为顶点的角与边;
(3)画出,使成平角,写出它的边.
17.(8分)如图,已知线段,,点M是AC的中点.
(1)求线段AM的长;
(2)在CB上取一点N,使得,求线段MN的长.
18.(10分)探究归纳题:
(1)试验分析:
如图1,经过一个顶点(如点A)可以作___________条对角线,它把四边形分为_________个三角形;
(2)拓展延伸:
运用(1)的分析方法,可得:图2过一个顶点作所有的对角线,把这个多边形分为_________个三角形;图3过一个顶点作所有的对角线,把这个多边形分为_________个三角形;
(3)探索归纳:对于n边形,过一个顶点的所有对角线把这个n边形分为_________个三角形.(用含n的式子表示)
(4)特例验证:过一个顶点的所有对角线可把十边形分为_________个三角形.
19.(10个)如图,已知,射线从位置出发,以每秒的速度按顺时针方向向射线旋转;与此同时,射线以每秒的速度,从位置出发按逆时针方向向射线旋转,到达射线后又以同样的速度按顺时针方向返回,当射线返回并与射线重合时,两条射线同时停止运动.设旋转时间为.
(1)当时,求的度数.
(2)当时,求t的值.
(3)在旋转过程中,是否存在t的值,使得 若存在,求出的值;若不存在,请说明理由.
20.(12分)如图,点A,O,B在同一条直线上,以O为端点,在直线AB的同侧画三条射线OC,OD,OE,射线OD平分,.
(1)射线OE平分吗?为什么?
(2)若,求的度数.
21.(12分)已知,射线BD在的内部,按要求完成下列各小题.
尝试探究:如图1,已知,当BD是的平分线时,的度数为________;
初步应用:如图2,已知,若BD不是的平分线,求的度数;
拓展提升:如图3,若时,试判断与之间的数量关系,并说明理由.
答案以及解析
1.答案:C
解析:因为两点之间线段最短,把弯曲的河道改直,能够缩短航程.故选C.
2.答案:B
解析:由题意可知,
,
,
,
,故选B.
3.答案:C
解析:作图如下:
由图可知:图形中小于平角的角有6个.
故选:C.
4.答案:B
解析:① 直线不可以度量,所以画直线是错误的;
②连接点A与点B的线段的长度,叫做A、B两点之间的距离,原说法错误;
③具有公共端点的两条射线组成的图形叫角,原说法错误;
④任何一个有理数都可以用数轴上的点来表示,原说法正确;
故正确答案有1个.
故选:B.
5.答案:D
解析:A.各边相等,各角都相等的多边形是正多边形,故选项错误,不符合题意;
B.若,点C不一定在线段AB上,故选项错误,不符合题意;
C.顶点在圆心,两条边与圆有交点所形成的角叫做圆心角,故选项错误,不符合题意;
D.钟表显示9点30分,此时时针与分针的夹角是105°,故选项正确,符合题意.
故选:D.
6.答案:B
解析:由图形可得,
,而与不一定相等,
不一定等于,
故①错误,不符合题意;
点C是AB的中点,
,
,
,
故②正确,符合题意;
点D是BC的中点,
,
,
故③正确,符合题意;
,
故④错误,不符合题意,
综上所述,成立的有:②③.
故选:B.
7.答案:B
解析:OM平分,ON平分,
,
,
,
,
即,
,
,
则,
故选:B.
8.答案:C
解析:当N在射线BA上时,,不合题意
当N在射线AB上时,,此时,
当N在线段AB上时,
由图可知,,
,
,
,
,
,
,
故选:C.
9.答案:B
解析:O是直线AB上一点,
,
,
,
平分,
,
,,
.
故选:B.
10.答案:C
解析:如图:射线是的三等分线,射线是的三等分线,
则,,
;
如图:射线是的三等分线,射线是的三等分线,
则,,
;
如图:射线是的三等分线,射线是的三等分线,
则,,
;
如图:射线是的三等分线,射线是的三等分线,
则,,
;
综上,为或或,
故选:C.
11.答案:;;
解析:①,
故答案为:;
②,
,
,
,
故答案为:;
③当时钟指向时间为时,时针走过小时,分钟走过分钟,
时针与0点的夹角为,
分针与0点的夹角为,
钟表上的时针与分针的夹角为,
故答案为:.
12.答案:8
解析:D,B,E三点依次在线段AC上,
,
,,
,.
点B为线段AC的中点,
.
13.答案:110°
解析:因为OE平分,所以.设.因为,所以,所以,所以.故答案为110°.
14.答案:(1)AD
(2)1或3
解析:(1)点D在线段AB上,如图:
,
故答案为:AD;
(2),,且,
当点D在线段AB上,如图:
;
当点D在线段BC上,如图:
;
故答案为:1或3.
15.答案:(1)30或90
(2)45或135
解析:(1)如图1,,,
则;
如图2,,,
则;
故答案为:30或90;
(2),分别是,的平分线,,
如图3,
,分别是,的平分线,
,,
,
,
;
如图4,
,分别是,的平分线,
,,
,
,
;
故答案为:45或135.
16.答案:(1)或或
(2)角为(或或),边是,
(3)图见解析,边是,
解析:(1)由图可得:
用三个字母表示以D为顶点的角为:,
用一个字母表示以D为顶点的角为:,
用数字表示以D为顶点的角为:,
故答案为:或或.
(2)由图可得:
用三个字母表示以B为顶点的角为:,
用一个字母表示以B为顶点的角为:,
用数字表示以B为顶点的角为:,
以B为顶点边是,,
故答案为:角为(或或),边是,.
(3)如图,是射线的反向延长线,
则成平角,的边是,.
17.答案:(1)4
(2)9
解析:(1)线段,,
,
又点M是AC的中点,
,即线段AM的长度是4;
(2),,
,
又点M是AC的中点,,
,
,即MN的长度是9.
18.答案:(1)1,2
(2)3,4
(3)
(4)8
解析:(1)如下图:
经过A点可以做1条对角线,它把四边形分为2个三角形,
故答案为:1,2;
(2)拓展延伸:
运用(1)的分析方法,可得:
图2过一个顶点,共有2条对角线,将这个多边形分为3个三角形;
图3过一个顶点,共有3条对角线,将这个多边形分为4个三角形;
故答案为:3,4;
(3)对于n边形,过一个顶点的所有对角线把这个n边形分为个三角形,
故答案为:;
(4)过一个顶点的所有对角线可把十边形分为个三角形,
故答案为:8.
19.答案:(1)
(2)当时,t的值为10或20
(3)存在或或,使得
解析:(1)当时,,,
(2)与相遇时间为(秒),
与重合时间为(秒),
与停止运动的时间为(秒),
①当时,
根据题意,得,
解得;
②当时,
根据题意,得,
解得;
③当时,
根据题意,得,
解得(不合题意,舍去)
综上所述,当时,t的值为10或20;
(3)①当时,
根据题意,得,
解得;
②当时,
根据题意,得,
解得;
③当时,
根据题意,得,
解得.
综上所述,存在或或,使得.
20.答案:(1)射线OE平分,理由见解析
(2)
解析:(1)设,
因为射线OD平分,
所以,
因为,
所以
因为点A,O,B在同一条直线上,
所以,
所以,
所以,
所以,
所以射线OE平分;
(2)因为,由(1)知,
所以,
解得,
所以.
21.答案:
解析:尝试探究:,BD平分,
所以,
因为,
所以.
所以.
初步应用:因为,
所以.
答:的度数为.
拓展提升:.
理由:因为,
所以.
1
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
