第四章 图形的相似(测能力)(含解析)——2023-2024学年北师大版数学九年级上册单元闯关双测卷
文档属性
| 名称 | 第四章 图形的相似(测能力)(含解析)——2023-2024学年北师大版数学九年级上册单元闯关双测卷 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 22:28:17 | ||
图片预览




文档简介
第四章 图形的相似(测能力)——2023-2024学年北师大版数学九年级上册单元闯关双测卷
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.如图所示,下列条件中能单独判断的个数是( )个.
①;
②;
③;
④.
A.1 B.2 C.3 D.4
2.如图,在中,D、E分别为、边的中点,连接,点F为边上一点,,连接交于点N,则下列结论中错误的是( )
A. B. C. D.
3.如图,在中,,,,点O是AB的中点,将沿射线CO平移,得到.当和重叠部分的面积是面积的一半时,平移的距离为( )
A. B. C. D.
4.已知,则( )
A.-3 B.3 C. D.
5.如图,在中,,,,点E是边CB上一动点,过点E作交AB于点F,D为线段EF的中点,按下列步骤作图:
①以C为圆心,适当长为半径画弧交CB,CA于点M,点N;
②分别以M,N为圆心,适当长为半径画弧,两弧的交点为G;
③作射线CG,若射线CG经过点D,则CE的长度为( )
A. B. C. D.
6.如图,在平面直角坐标系中,等边三角形的顶点,,已知与位似,位似中心是原点O,且的面积是面积的4倍,则点A对应点的坐标为( )
A.或 B.或
C.或 D.或
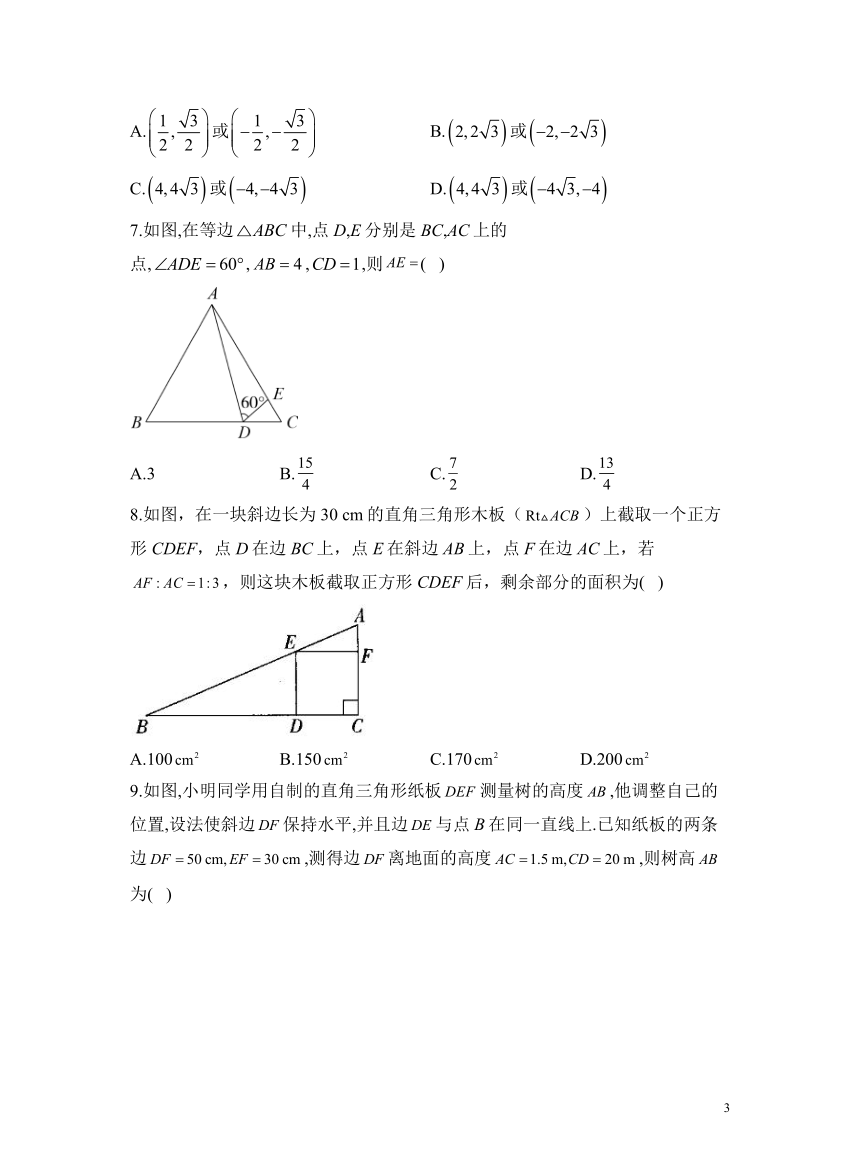
7.如图,在等边中,点D,E分别是BC,AC上的点,,,,则( )
A.3 B. C. D.
8.如图,在一块斜边长为30 cm的直角三角形木板()上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A.100 B.150 C.170 D.200
9.如图,小明同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.已知纸板的两条边,测得边离地面的高度,则树高为( )
A.12m B.13.5m C.15m D.16.5m
10.如图,四边形为矩形,且,,点E为上一点且,连接、,且,,连接,则的长为( )
A.10 B. C. D.
二、填空题(每小题4分,共20分)
11.已知,则的值为_________.
12.如图,在中,E为CD上一点,连接AE,BD交于点F,,则__________.
13.如图,已知在中,点分别是边上的点,,且,那么等于____________.
14.如图,在中,,,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q同时从点B开始沿BC边运动,速度为3cm/s的速度,当P,Q运动________时,与相似.
15.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木 ”用今天的话说,大意是:如图,是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于的中点,南门K位于的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在上) 请你计算的长为__________步.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,并给出了格点(顶点为网格线的交点).
(1)画出关于y轴对称的;
(2)以点O为位似中心,将作位似变换得到,使得,画出位似变换后的,此时点坐标为________;
(3)和之间的位置关系为________.
17.(8分)请阅读以下材料,并完成相应的问题:
角平分线分线段成比例定理,如图1,在中,AD平分,则.
下面是这个定理的部分证明过程.
证明:如图2,过点C作.交BA的延长线于点E.
任务:
(1)请按照上面的证明思路,写出该证明过程的剩余部分;
(2)如图3,已知中,,,,AD平分,求的周长.
18.(10分)如图,在平行四边形ABCD,F是边BC上一点,连接DF并延长,交AB的延长线于E,且.
(1)求证:;
(2)如果,,,求BE的长.
19.(10分)小优和小莉住在同一小区, 小区内有两栋高度均为40m 的楼AB,CD, 如图, 他们打算用学过的数学 知识测量这两栋楼之间的距离BD. 他们在BD 上确定一点E, 并在E 处的地面上放置一个小平面镜 (大小忽略不计), 小优沿着 BE方向移动, 当移动到点G 处时, 他刚好在小平面镜内看到楼AB 的顶 端A 的像, 此时测得, 小优眼睛与地面的距离; 他们又在BD 上的点 M处坚立起 一个高 的标杆MH, 小莉沿着DM 方向移动, 当移动到点P 处时, 她恰好看到标杆顶端H 与楼CD 的顶端C 重合, 此时测得小莉眼睛与地面的距离,,. 已知AB, FG,NP,HM,CD均与BD 垂直, 所有点在同一平面内. 请根据以上信息, 求这两栋楼之间的距离BD.
20.(12分)如图,已知中,CD为AB边上的中线,点G在AC的延长线上,且.
(1)沿AC方向平移,得到,使得点C与点G重合,点A的对应点为点E,点B的对应点为点F.(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,设EF与CD,BC分别交于点M,N,求证:M,N为线段EF的三等分点.
21.(12分)已知在中,,,,D为BC边上的一点.过点D作射线,分别交边AB,AC于点E,F.
(1)当D为BC的中点,且,时,如图①,______.
(2)①若D为BC的中点,将绕点D旋转到图②位置时,______.
②若改变点D的位置,且时,求的值,请就图③的情形写出解答过程.
(3)如图③连接EF,当______时,与相似.
答案以及解析
1.答案:C
解析:有三个,
①,再加上为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
②,再加上为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
③中不是已知的比例线段的夹角,不正确
④可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定;
故选C.
2.答案:C
解析:D、E分别为、边的中点,
.
.
,,.
.
,
.
.
所以A,B,D正确,C错误;
故选:C.
3.答案:C
解析:,,,.
点O是AB的中点,.如图,由平移易知,点O是DE的中点,,,,.
4.答案:C
解析:,,,,;故选C.
5.答案:C
解析:,,,
,
由作法得CD平分,
,
,
,
,
,
D点为EF的中点,
,
设,则,,
,
,
,即,解得,
即CE的长为.
故选:C.
6.答案:B
解析:等边三角形的顶点,,
,
过A作轴于C,
是等边三角形,
,,
,
与位似,位似中心是原点O,且的面积是面积的4倍,
与位似为2比1,
点A的对应点的坐标是或,即或,
故选:B.
7.答案:D
解析:,
,
,
,
又,
,
,
等边中,,,设,
,,
,
,
;
故选:D.
8.答案:A
解析:设cm,则cm,四边形CDEF为正方形, cm,,,, cm,在中,,即,解得(舍负),cm, cm, cm,剩余部分的面积(),故选A.
9.答案:D
解析:,
,
.
在中,,由勾股定理得.
又,
,解得,
.故选D.
10.答案:C
解析:过点F作于点G,如图所示:
四边形为矩形,
,,,
,
,
,
,
,
,
设,则,
则,
即,
整理得:,
解得:,,
,
,
,
,
,,
,
设,则,
,
,
解得:,(舍去),
,
,
,
,
,
,
,,
,
,故C正确.
故选:C.
11.答案:/
解析:,
,
,
故答案为:.
12.答案:2:3
解析:四边形ABCD为平行四边形,
,,
,,
,
,
即,
,
则,
故答案为2:3
13.答案:
解析:,
,即.
设,则.
.
14.答案:S或S
解析:,,,
,
当时,,即,解得,
当时,,即,解得,
当时,,即,解得,
即当S或S时,由P,B,Q三点连成的三角形与相似.
故答案为:或.
15.答案:
解析:∵四边形是正方形,
,
.
,
.
又,
,则,
分别为的中点,
步,
,解得步.
16.答案:(1)见解析;
(2)图见解析,;
(3)
解析:(1)如图,即为所求.
(2)如图,即为所求,点坐标为.
(3).
故答案为:.
17.答案:(1)见解析
(2)
解析:(1)证明:如图2,过C作.交BA的延长线于E,
,
,,,
,
,
,
.
(2)如图3,,,,
,
AD平分,
,即,
,
,
的周长.
18.答案:(1)见解析
(2)5
解析:(1)证明:四边形ABCD是平行四边形,
,,
,
,
,
;
(2),
,
即,
,
,
,
,
即,
又,
.
19.答案:60m
解析:由题意知 ,
,
即
如图, 过点N 作CD 的垂线, 分别交 HM,CD于点O, Q ,
则易知,,,
,
,
,,
,
,
即,
,
20.答案:(1)见解析
(2)证明见解析
解析:(1)如图,即为所求.(作法不唯一)
(2)证明:由平移的性质可得,,,.
,,
,
即.
,
,
.
同理可得,
.
是AB边上的中线,
,,
,即M,N是线段EF的三等分点.
21.答案:(1)3
(2)①3;
②
(3)或
解析:(1),,,
,,
点D是BC的中点,
,DF是的中位线,
,,
,
故答案为:3;
(2)①过点D作于点M,于点N,如图所示:
则,
四边形AMDN是矩形,
,
即,
,
,
即,
,
,
,
同(1)得:,
故答案为:3;
②过点P作于点P,于点Q,如图所示:
,
四边形APDQ是矩形,
,,
,,,
,
,,
,,
,,
,,
,,
与①同理得:,
(3)如图,在中,
由勾股定理得:
,
与相似分两种情况:
①,则,
即,整理得:,
,
;
(2),则,
即,
整理得:,
,
;
综上所述,当或时,与相似;
故答案为:或.
1
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.如图所示,下列条件中能单独判断的个数是( )个.
①;
②;
③;
④.
A.1 B.2 C.3 D.4
2.如图,在中,D、E分别为、边的中点,连接,点F为边上一点,,连接交于点N,则下列结论中错误的是( )
A. B. C. D.
3.如图,在中,,,,点O是AB的中点,将沿射线CO平移,得到.当和重叠部分的面积是面积的一半时,平移的距离为( )
A. B. C. D.
4.已知,则( )
A.-3 B.3 C. D.
5.如图,在中,,,,点E是边CB上一动点,过点E作交AB于点F,D为线段EF的中点,按下列步骤作图:
①以C为圆心,适当长为半径画弧交CB,CA于点M,点N;
②分别以M,N为圆心,适当长为半径画弧,两弧的交点为G;
③作射线CG,若射线CG经过点D,则CE的长度为( )
A. B. C. D.
6.如图,在平面直角坐标系中,等边三角形的顶点,,已知与位似,位似中心是原点O,且的面积是面积的4倍,则点A对应点的坐标为( )
A.或 B.或
C.或 D.或
7.如图,在等边中,点D,E分别是BC,AC上的点,,,,则( )
A.3 B. C. D.
8.如图,在一块斜边长为30 cm的直角三角形木板()上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A.100 B.150 C.170 D.200
9.如图,小明同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.已知纸板的两条边,测得边离地面的高度,则树高为( )
A.12m B.13.5m C.15m D.16.5m
10.如图,四边形为矩形,且,,点E为上一点且,连接、,且,,连接,则的长为( )
A.10 B. C. D.
二、填空题(每小题4分,共20分)
11.已知,则的值为_________.
12.如图,在中,E为CD上一点,连接AE,BD交于点F,,则__________.
13.如图,已知在中,点分别是边上的点,,且,那么等于____________.
14.如图,在中,,,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q同时从点B开始沿BC边运动,速度为3cm/s的速度,当P,Q运动________时,与相似.
15.《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木 ”用今天的话说,大意是:如图,是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于的中点,南门K位于的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在上) 请你计算的长为__________步.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,并给出了格点(顶点为网格线的交点).
(1)画出关于y轴对称的;
(2)以点O为位似中心,将作位似变换得到,使得,画出位似变换后的,此时点坐标为________;
(3)和之间的位置关系为________.
17.(8分)请阅读以下材料,并完成相应的问题:
角平分线分线段成比例定理,如图1,在中,AD平分,则.
下面是这个定理的部分证明过程.
证明:如图2,过点C作.交BA的延长线于点E.
任务:
(1)请按照上面的证明思路,写出该证明过程的剩余部分;
(2)如图3,已知中,,,,AD平分,求的周长.
18.(10分)如图,在平行四边形ABCD,F是边BC上一点,连接DF并延长,交AB的延长线于E,且.
(1)求证:;
(2)如果,,,求BE的长.
19.(10分)小优和小莉住在同一小区, 小区内有两栋高度均为40m 的楼AB,CD, 如图, 他们打算用学过的数学 知识测量这两栋楼之间的距离BD. 他们在BD 上确定一点E, 并在E 处的地面上放置一个小平面镜 (大小忽略不计), 小优沿着 BE方向移动, 当移动到点G 处时, 他刚好在小平面镜内看到楼AB 的顶 端A 的像, 此时测得, 小优眼睛与地面的距离; 他们又在BD 上的点 M处坚立起 一个高 的标杆MH, 小莉沿着DM 方向移动, 当移动到点P 处时, 她恰好看到标杆顶端H 与楼CD 的顶端C 重合, 此时测得小莉眼睛与地面的距离,,. 已知AB, FG,NP,HM,CD均与BD 垂直, 所有点在同一平面内. 请根据以上信息, 求这两栋楼之间的距离BD.
20.(12分)如图,已知中,CD为AB边上的中线,点G在AC的延长线上,且.
(1)沿AC方向平移,得到,使得点C与点G重合,点A的对应点为点E,点B的对应点为点F.(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,设EF与CD,BC分别交于点M,N,求证:M,N为线段EF的三等分点.
21.(12分)已知在中,,,,D为BC边上的一点.过点D作射线,分别交边AB,AC于点E,F.
(1)当D为BC的中点,且,时,如图①,______.
(2)①若D为BC的中点,将绕点D旋转到图②位置时,______.
②若改变点D的位置,且时,求的值,请就图③的情形写出解答过程.
(3)如图③连接EF,当______时,与相似.
答案以及解析
1.答案:C
解析:有三个,
①,再加上为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
②,再加上为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
③中不是已知的比例线段的夹角,不正确
④可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定;
故选C.
2.答案:C
解析:D、E分别为、边的中点,
.
.
,,.
.
,
.
.
所以A,B,D正确,C错误;
故选:C.
3.答案:C
解析:,,,.
点O是AB的中点,.如图,由平移易知,点O是DE的中点,,,,.
4.答案:C
解析:,,,,;故选C.
5.答案:C
解析:,,,
,
由作法得CD平分,
,
,
,
,
,
D点为EF的中点,
,
设,则,,
,
,
,即,解得,
即CE的长为.
故选:C.
6.答案:B
解析:等边三角形的顶点,,
,
过A作轴于C,
是等边三角形,
,,
,
与位似,位似中心是原点O,且的面积是面积的4倍,
与位似为2比1,
点A的对应点的坐标是或,即或,
故选:B.
7.答案:D
解析:,
,
,
,
又,
,
,
等边中,,,设,
,,
,
,
;
故选:D.
8.答案:A
解析:设cm,则cm,四边形CDEF为正方形, cm,,,, cm,在中,,即,解得(舍负),cm, cm, cm,剩余部分的面积(),故选A.
9.答案:D
解析:,
,
.
在中,,由勾股定理得.
又,
,解得,
.故选D.
10.答案:C
解析:过点F作于点G,如图所示:
四边形为矩形,
,,,
,
,
,
,
,
,
设,则,
则,
即,
整理得:,
解得:,,
,
,
,
,
,,
,
设,则,
,
,
解得:,(舍去),
,
,
,
,
,
,
,,
,
,故C正确.
故选:C.
11.答案:/
解析:,
,
,
故答案为:.
12.答案:2:3
解析:四边形ABCD为平行四边形,
,,
,,
,
,
即,
,
则,
故答案为2:3
13.答案:
解析:,
,即.
设,则.
.
14.答案:S或S
解析:,,,
,
当时,,即,解得,
当时,,即,解得,
当时,,即,解得,
即当S或S时,由P,B,Q三点连成的三角形与相似.
故答案为:或.
15.答案:
解析:∵四边形是正方形,
,
.
,
.
又,
,则,
分别为的中点,
步,
,解得步.
16.答案:(1)见解析;
(2)图见解析,;
(3)
解析:(1)如图,即为所求.
(2)如图,即为所求,点坐标为.
(3).
故答案为:.
17.答案:(1)见解析
(2)
解析:(1)证明:如图2,过C作.交BA的延长线于E,
,
,,,
,
,
,
.
(2)如图3,,,,
,
AD平分,
,即,
,
,
的周长.
18.答案:(1)见解析
(2)5
解析:(1)证明:四边形ABCD是平行四边形,
,,
,
,
,
;
(2),
,
即,
,
,
,
,
即,
又,
.
19.答案:60m
解析:由题意知 ,
,
即
如图, 过点N 作CD 的垂线, 分别交 HM,CD于点O, Q ,
则易知,,,
,
,
,,
,
,
即,
,
20.答案:(1)见解析
(2)证明见解析
解析:(1)如图,即为所求.(作法不唯一)
(2)证明:由平移的性质可得,,,.
,,
,
即.
,
,
.
同理可得,
.
是AB边上的中线,
,,
,即M,N是线段EF的三等分点.
21.答案:(1)3
(2)①3;
②
(3)或
解析:(1),,,
,,
点D是BC的中点,
,DF是的中位线,
,,
,
故答案为:3;
(2)①过点D作于点M,于点N,如图所示:
则,
四边形AMDN是矩形,
,
即,
,
,
即,
,
,
,
同(1)得:,
故答案为:3;
②过点P作于点P,于点Q,如图所示:
,
四边形APDQ是矩形,
,,
,,,
,
,,
,,
,,
,,
,,
与①同理得:,
(3)如图,在中,
由勾股定理得:
,
与相似分两种情况:
①,则,
即,整理得:,
,
;
(2),则,
即,
整理得:,
,
;
综上所述,当或时,与相似;
故答案为:或.
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
