第五章 投影与视图(测基础)(含解析)——2023-2024学年北师大版数学九年级上册单元闯关双测卷
文档属性
| 名称 | 第五章 投影与视图(测基础)(含解析)——2023-2024学年北师大版数学九年级上册单元闯关双测卷 |  | |
| 格式 | docx | ||
| 文件大小 | 586.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 22:29:14 | ||
图片预览


文档简介
第五章 投影与视图(测基础)——2023-2024学年北师大版数学九年级上册单元闯关双测卷
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.下列光线所形成的投影是平行投影的是( )
A.太阳光线 B.台灯的光线 C.手电筒的光线 D.路灯的光线
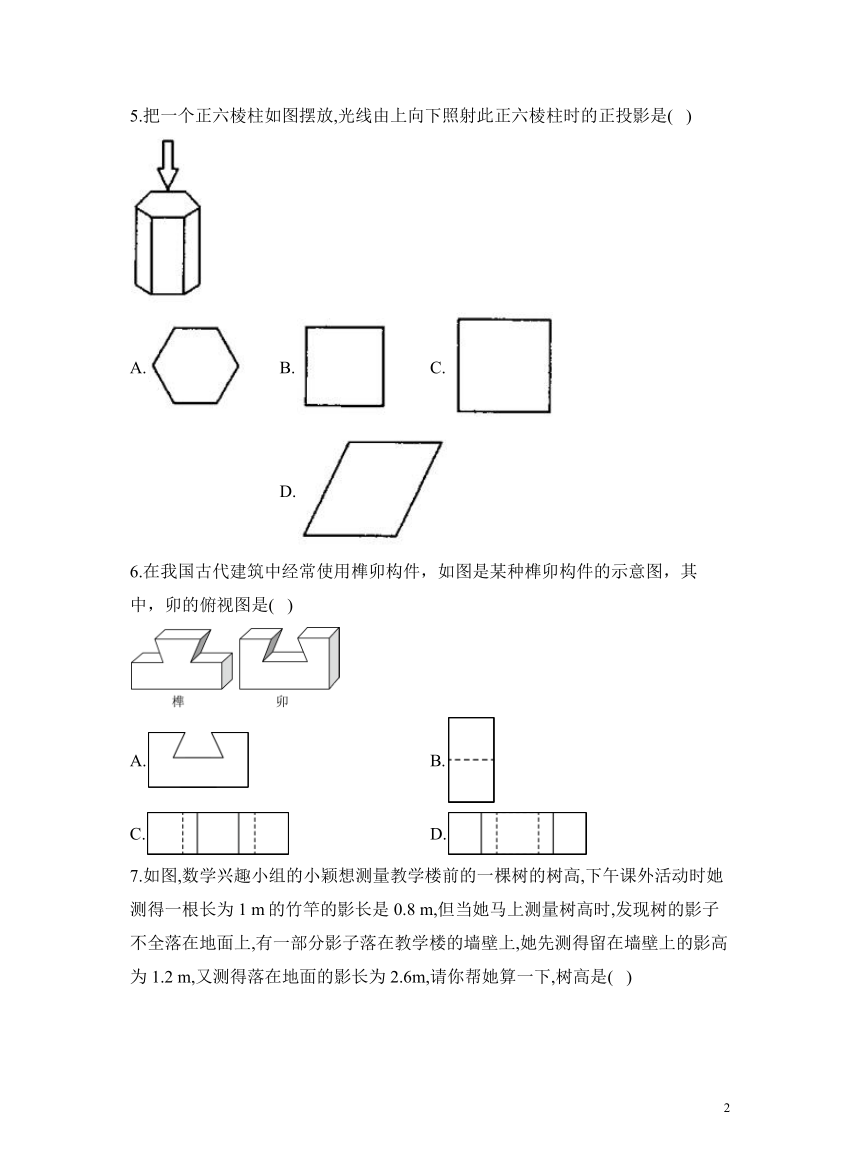
2.如图所示的几何体的主视图是( )
A. B. C. D.
3.在下列四幅图形中,能表示两棵小树在同一时刻阳光下影子的图形的可能是( )
A. B.
C. D.
4.榫卯是我国古代建筑、家具的一种结构方式,它通过两个构件上凹凸部位相结合来将不同构件组合在一起,如图是其中一种榫,其主视图是( )
A. B. C. D.
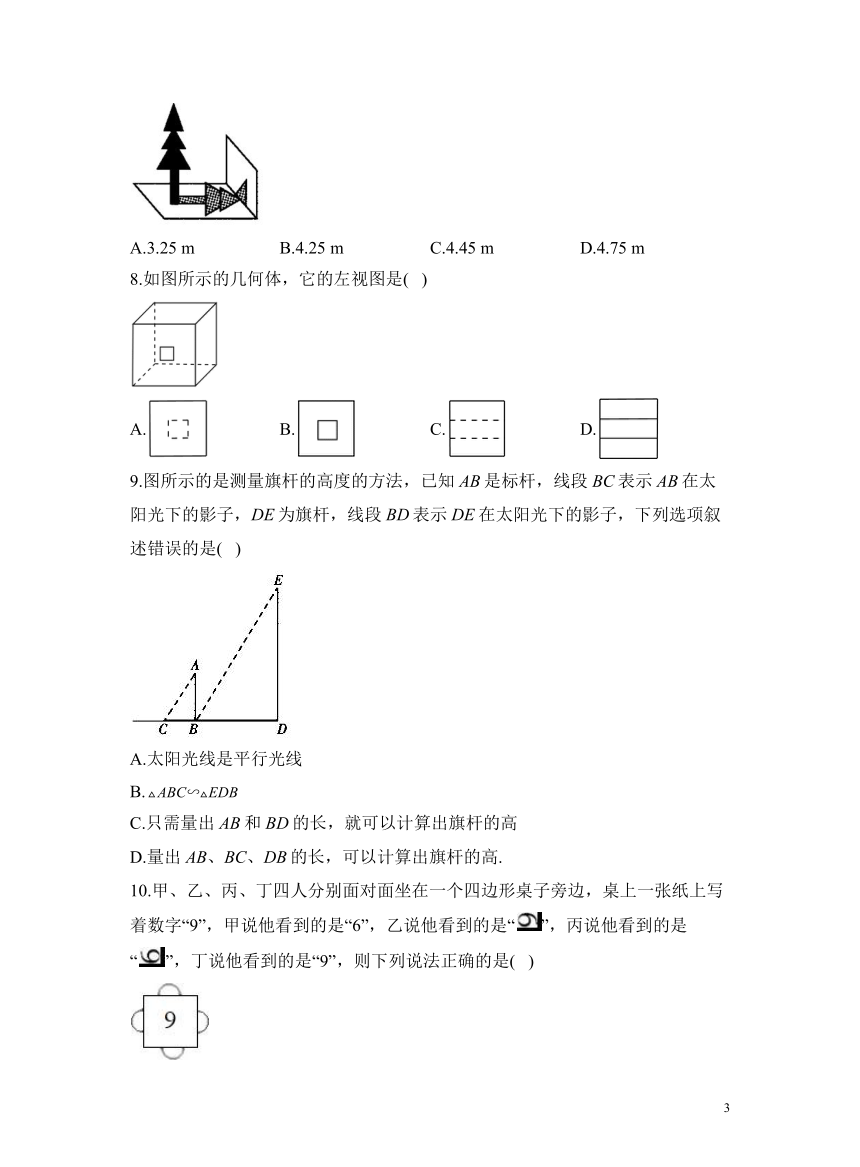
5.把一个正六棱柱如图摆放,光线由上向下照射此正六棱柱时的正投影是( )
A. B. C. D.
6.在我国古代建筑中经常使用榫卯构件,如图是某种榫卯构件的示意图,其中,卯的俯视图是( )
A. B.
C. D.
7.如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1 m的竹竿的影长是0.8 m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,她先测得留在墙壁上的影高为1.2 m,又测得落在地面的影长为2.6m,请你帮她算一下,树高是( )
A.3.25 m B.4.25 m C.4.45 m D.4.75 m
8.如图所示的几何体,它的左视图是( )
A. B. C. D.
9.图所示的是测量旗杆的高度的方法,已知AB是标杆,线段BC表示AB在太阳光下的影子,DE为旗杆,线段BD表示DE在太阳光下的影子,下列选项叙述错误的是( )
A.太阳光线是平行光线
B.
C.只需量出AB和BD的长,就可以计算出旗杆的高
D.量出AB、BC、DB的长,可以计算出旗杆的高.
10.甲、乙、丙、丁四人分别面对面坐在一个四边形桌子旁边,桌上一张纸上写着数字“9”,甲说他看到的是“6”,乙说他看到的是“”,丙说他看到的是“”,丁说他看到的是“9”,则下列说法正确的是( )
A.甲在丁的对面,乙在甲的左边,丙在丁的右边
B.丙在乙的对面,丙的左边是甲,右边是乙
C.甲在乙的对面,甲的右边是丙,左边是丁
D.甲在丁的对面,乙在甲的右边,丙在丁的右边
二、填空题(每小题4分,共20分)
11.图所示的几何体中,主视图的轮廓是三角形的是_____________.
12.古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长3米,它的影长FD是6米,同一时刻测得OA是286米,则金字塔的高度OB是_______米.
13.如图,小明在A时测得某树的影长为8m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为____________.
14.如图,一块直角三角尺,,测得边的中心投影的长为24 cm,则的长为___________cm.
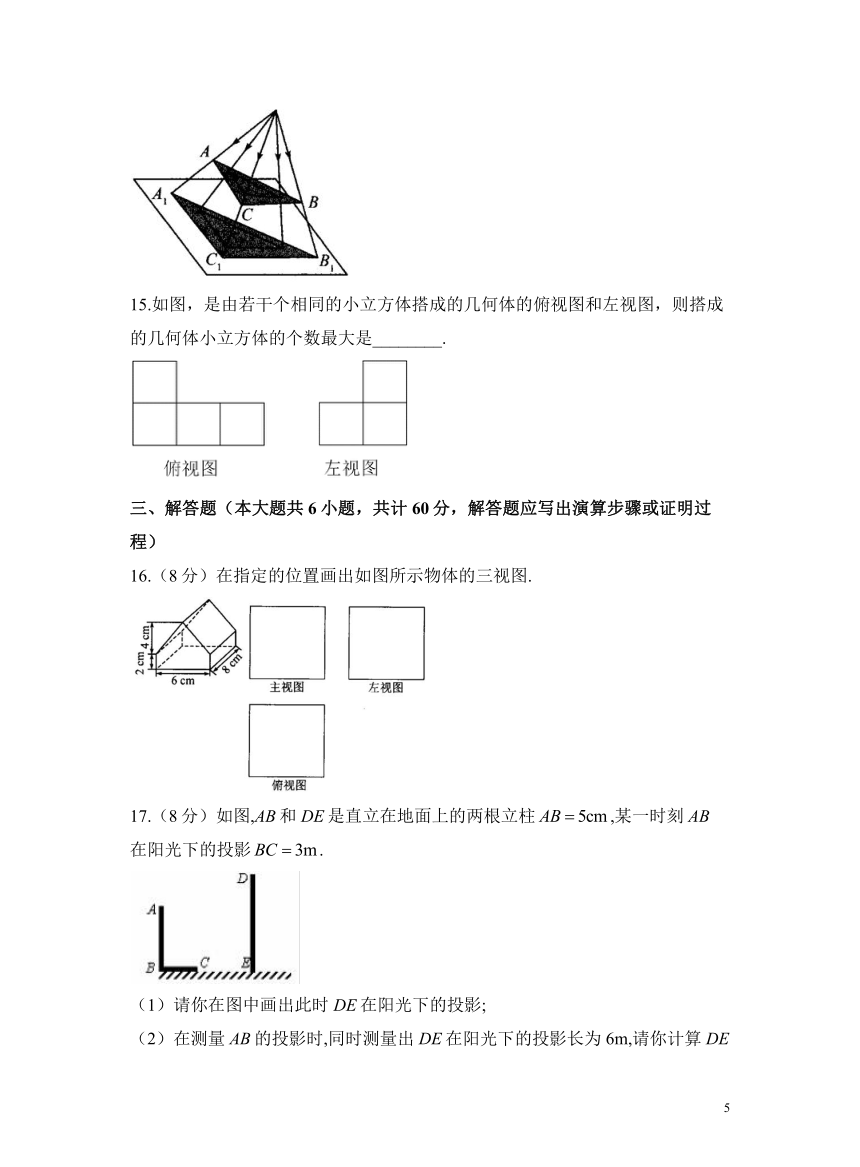
15.如图,是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则搭成的几何体小立方体的个数最大是________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)在指定的位置画出如图所示物体的三视图.
17.(8分)如图,AB和DE是直立在地面上的两根立柱,某一时刻AB在阳光下的投影.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
18.(10分)如图①,一个工件是由大长方体上面中间部位挖去一个小长方体后形成的,主视图是凹字形的轴对称图形.
(1)请在图②中合适的位置补画该工件的俯视图;
(2)若该工件表面需涂油漆,根据图中尺寸(单位:cm),计算需涂油漆的面积.
19.(10分)小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图所示,此时测得地面上的影长为8米,坡面上的影长为4米已知斜坡的坡角为30°,同一时刻,一根长为1米,垂直于地面放置的标杆在地面上的影长为2米,请计算出树的高度.
20.(12分)由几个相同的棱长为1的小正方体搭成的几何体的俯视图如图(1)所示,格中的数字表示该位置的小正方体的个数.
(1)请在图(2)中分别画出这个几何体的主视图和左视图;
(2)根据三视图,求这个组合几何体的表面积.(包括底面积)
(3)若用上述小正方体搭成的几何体的俯视图不变,各位置的小正方体个数可以改变(总数目不变),要使搭成的组合几何体的表面积最大(包括底面积),应该怎么搭,请仿照图(1),将数字填写在图(3)的正方形中.
21.(12分)学习投影后,小红、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6 m的小红()的影子的长是3,而小颖()刚好在路灯灯泡的正下方H点,并测得.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度;
(3)如果小红沿线段向小颖()走去,当小红走到中点处时,求其影子的长;当小红继续走剩下路程的到处时,求其影子的长;当小红继续走剩下路程的到处,…,按此规律继续走下去,当小红走剩下路程的到处时,其影子的长为__________m(直接用n的代数式表示).
答案以及解析
1.答案:A
解析:四个选项中只有太阳光可认为是平行光线;故太阳光线下形成的投影是平行投影.故选A.
2.答案:B
解析:从正面看,是一个矩形,矩形的中间有一条纵向的实线.故选B.
3.答案:D
解析:A.影子的方向不相同,故本选项错误;
B.影子的方向不相同,故本选项错误;
C.相同树高与影子是成正比的,较高的树的影子长度小于较低的树的影子,故本选项错误;
D.影子平行,且较高的树的影子长度大于较低的树的影子,故本选项正确;故选D.
4.答案:B
解析:该几何体的主视图是:
故选:B.
5.答案:A
解析:光线由上向下照射此正六棱柱时的正投影是从上向下看该几何体得到的平面图形,应为.
6.答案:C
解析:卯的俯视图是,故选C.
7.答案:C
解析:如图,设是在地面上的影子,树高为,
∵一根长为1 m的竹竿的影长是0.8 m,,
,即.
∴树在地面上的实际影长是0.96+2.6=3.56(m).
根据竹竿的高与其影子的比值和树高与其影子的比值相同,得,解得.
∴树高是4.45 m.
8.答案:C
解析:该几何体的左视图如选项C所示,故选C.
9.答案:C
解析:由太阳光线是平行光线,可得,又,,,,即已知AB、BC、DB的长,可以计算出旗杆的高,故A,B,D中叙述正确,不符合题意;C中,只量出AB和BD的长,不知道BC的长,不能求出旗杆的高,故C中叙述错误,符合题意.故选C.
10.答案:D
解析:由题意可得,甲说他看到的是“6,丁说他看到的是“9”,
说明两人坐对面,乙和丙坐对面,
又乙说他看到的是“”,
乙在甲右边,则丙在丁右边.
故选D.
11.答案:②③
解析:①的主视图的轮廓是矩形;②的主视图的轮廓是三角形,③的主视图的轮廓是等腰三角形,故答案是②③.
12.答案:143
解析:据相同时刻的物高与影长成比例,
设金字塔的高度BO为x米,则可列比例为,
解得:,
经检验,是原方程的解,
.
故答案为:143.
13.答案:
解析:根据题意,作 ,树高为CD ,且 ,
,
,
,
,即 ,解得.
故答案为: 4 .
14.答案:
解析:,.,,.
15.答案:7
解析:由俯视图易得最底层有4个立方体,由左视图易得第二层最多有3个立方体和最少有1个立方体,
那么小立方体的个数可能是5个或6个或7个.
故答案为:7.
16.答案:
解析:该物体的三视图如图所示
17.解析:(1)连接AC,过点D作,交直线BC于点F,线段EF即为DE的投影.
(2),
.
,
.
,
(m).
18.答案:(1)俯视图如图所示.
(2).
答:需涂油漆的面积为.
19.答案:如图,延长AC交直线BD于点F,过点C作于点E.
在中,米,,则米,所以米.
根据同一时刻物高与影长对应成比例,得,则米,
所以米.
又,所以米,所以树的高度为米.
20.答案:(1)这个几何体的主视图和左视图如图所示:
(2)由俯视图知,上表面共有3个小正方形,下表面共有3个小正方形;由左视图知,左表面共有4个小正方形,右表面共有4个小正方形;由主视图知,前表面共有5个小正方形,后表面共有5个小正方形.
每个小正方形的面积为1,故这个组合几何体的表面积为.
(3)(答案不唯一)要使表面积最大,则需满足两个小正方体重合的面最少,此时俯视图如下:
21.解析:(1)如图所示.
(2),
.
,
.
(3)同(2)得,
.
设长为,则,
解得,即.
同理,,
解得.
,
解得.
1
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.下列光线所形成的投影是平行投影的是( )
A.太阳光线 B.台灯的光线 C.手电筒的光线 D.路灯的光线
2.如图所示的几何体的主视图是( )
A. B. C. D.
3.在下列四幅图形中,能表示两棵小树在同一时刻阳光下影子的图形的可能是( )
A. B.
C. D.
4.榫卯是我国古代建筑、家具的一种结构方式,它通过两个构件上凹凸部位相结合来将不同构件组合在一起,如图是其中一种榫,其主视图是( )
A. B. C. D.
5.把一个正六棱柱如图摆放,光线由上向下照射此正六棱柱时的正投影是( )
A. B. C. D.
6.在我国古代建筑中经常使用榫卯构件,如图是某种榫卯构件的示意图,其中,卯的俯视图是( )
A. B.
C. D.
7.如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1 m的竹竿的影长是0.8 m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,她先测得留在墙壁上的影高为1.2 m,又测得落在地面的影长为2.6m,请你帮她算一下,树高是( )
A.3.25 m B.4.25 m C.4.45 m D.4.75 m
8.如图所示的几何体,它的左视图是( )
A. B. C. D.
9.图所示的是测量旗杆的高度的方法,已知AB是标杆,线段BC表示AB在太阳光下的影子,DE为旗杆,线段BD表示DE在太阳光下的影子,下列选项叙述错误的是( )
A.太阳光线是平行光线
B.
C.只需量出AB和BD的长,就可以计算出旗杆的高
D.量出AB、BC、DB的长,可以计算出旗杆的高.
10.甲、乙、丙、丁四人分别面对面坐在一个四边形桌子旁边,桌上一张纸上写着数字“9”,甲说他看到的是“6”,乙说他看到的是“”,丙说他看到的是“”,丁说他看到的是“9”,则下列说法正确的是( )
A.甲在丁的对面,乙在甲的左边,丙在丁的右边
B.丙在乙的对面,丙的左边是甲,右边是乙
C.甲在乙的对面,甲的右边是丙,左边是丁
D.甲在丁的对面,乙在甲的右边,丙在丁的右边
二、填空题(每小题4分,共20分)
11.图所示的几何体中,主视图的轮廓是三角形的是_____________.
12.古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长3米,它的影长FD是6米,同一时刻测得OA是286米,则金字塔的高度OB是_______米.
13.如图,小明在A时测得某树的影长为8m,B时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为____________.
14.如图,一块直角三角尺,,测得边的中心投影的长为24 cm,则的长为___________cm.
15.如图,是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则搭成的几何体小立方体的个数最大是________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)在指定的位置画出如图所示物体的三视图.
17.(8分)如图,AB和DE是直立在地面上的两根立柱,某一时刻AB在阳光下的投影.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
18.(10分)如图①,一个工件是由大长方体上面中间部位挖去一个小长方体后形成的,主视图是凹字形的轴对称图形.
(1)请在图②中合适的位置补画该工件的俯视图;
(2)若该工件表面需涂油漆,根据图中尺寸(单位:cm),计算需涂油漆的面积.
19.(10分)小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图所示,此时测得地面上的影长为8米,坡面上的影长为4米已知斜坡的坡角为30°,同一时刻,一根长为1米,垂直于地面放置的标杆在地面上的影长为2米,请计算出树的高度.
20.(12分)由几个相同的棱长为1的小正方体搭成的几何体的俯视图如图(1)所示,格中的数字表示该位置的小正方体的个数.
(1)请在图(2)中分别画出这个几何体的主视图和左视图;
(2)根据三视图,求这个组合几何体的表面积.(包括底面积)
(3)若用上述小正方体搭成的几何体的俯视图不变,各位置的小正方体个数可以改变(总数目不变),要使搭成的组合几何体的表面积最大(包括底面积),应该怎么搭,请仿照图(1),将数字填写在图(3)的正方形中.
21.(12分)学习投影后,小红、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6 m的小红()的影子的长是3,而小颖()刚好在路灯灯泡的正下方H点,并测得.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度;
(3)如果小红沿线段向小颖()走去,当小红走到中点处时,求其影子的长;当小红继续走剩下路程的到处时,求其影子的长;当小红继续走剩下路程的到处,…,按此规律继续走下去,当小红走剩下路程的到处时,其影子的长为__________m(直接用n的代数式表示).
答案以及解析
1.答案:A
解析:四个选项中只有太阳光可认为是平行光线;故太阳光线下形成的投影是平行投影.故选A.
2.答案:B
解析:从正面看,是一个矩形,矩形的中间有一条纵向的实线.故选B.
3.答案:D
解析:A.影子的方向不相同,故本选项错误;
B.影子的方向不相同,故本选项错误;
C.相同树高与影子是成正比的,较高的树的影子长度小于较低的树的影子,故本选项错误;
D.影子平行,且较高的树的影子长度大于较低的树的影子,故本选项正确;故选D.
4.答案:B
解析:该几何体的主视图是:
故选:B.
5.答案:A
解析:光线由上向下照射此正六棱柱时的正投影是从上向下看该几何体得到的平面图形,应为.
6.答案:C
解析:卯的俯视图是,故选C.
7.答案:C
解析:如图,设是在地面上的影子,树高为,
∵一根长为1 m的竹竿的影长是0.8 m,,
,即.
∴树在地面上的实际影长是0.96+2.6=3.56(m).
根据竹竿的高与其影子的比值和树高与其影子的比值相同,得,解得.
∴树高是4.45 m.
8.答案:C
解析:该几何体的左视图如选项C所示,故选C.
9.答案:C
解析:由太阳光线是平行光线,可得,又,,,,即已知AB、BC、DB的长,可以计算出旗杆的高,故A,B,D中叙述正确,不符合题意;C中,只量出AB和BD的长,不知道BC的长,不能求出旗杆的高,故C中叙述错误,符合题意.故选C.
10.答案:D
解析:由题意可得,甲说他看到的是“6,丁说他看到的是“9”,
说明两人坐对面,乙和丙坐对面,
又乙说他看到的是“”,
乙在甲右边,则丙在丁右边.
故选D.
11.答案:②③
解析:①的主视图的轮廓是矩形;②的主视图的轮廓是三角形,③的主视图的轮廓是等腰三角形,故答案是②③.
12.答案:143
解析:据相同时刻的物高与影长成比例,
设金字塔的高度BO为x米,则可列比例为,
解得:,
经检验,是原方程的解,
.
故答案为:143.
13.答案:
解析:根据题意,作 ,树高为CD ,且 ,
,
,
,
,即 ,解得.
故答案为: 4 .
14.答案:
解析:,.,,.
15.答案:7
解析:由俯视图易得最底层有4个立方体,由左视图易得第二层最多有3个立方体和最少有1个立方体,
那么小立方体的个数可能是5个或6个或7个.
故答案为:7.
16.答案:
解析:该物体的三视图如图所示
17.解析:(1)连接AC,过点D作,交直线BC于点F,线段EF即为DE的投影.
(2),
.
,
.
,
(m).
18.答案:(1)俯视图如图所示.
(2).
答:需涂油漆的面积为.
19.答案:如图,延长AC交直线BD于点F,过点C作于点E.
在中,米,,则米,所以米.
根据同一时刻物高与影长对应成比例,得,则米,
所以米.
又,所以米,所以树的高度为米.
20.答案:(1)这个几何体的主视图和左视图如图所示:
(2)由俯视图知,上表面共有3个小正方形,下表面共有3个小正方形;由左视图知,左表面共有4个小正方形,右表面共有4个小正方形;由主视图知,前表面共有5个小正方形,后表面共有5个小正方形.
每个小正方形的面积为1,故这个组合几何体的表面积为.
(3)(答案不唯一)要使表面积最大,则需满足两个小正方体重合的面最少,此时俯视图如下:
21.解析:(1)如图所示.
(2),
.
,
.
(3)同(2)得,
.
设长为,则,
解得,即.
同理,,
解得.
,
解得.
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
