第五章 投影与视图(测能力)(含解析)——2023-2024学年北师大版数学九年级上册单元闯关双测卷
文档属性
| 名称 | 第五章 投影与视图(测能力)(含解析)——2023-2024学年北师大版数学九年级上册单元闯关双测卷 |

|
|
| 格式 | docx | ||
| 文件大小 | 519.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 00:00:00 | ||
图片预览


文档简介
第五章 投影与视图(测能力)——2023-2024学年北师大版数学九年级上册单元闯关双测卷
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.下列各种现象属于中心投影现象的是( )
A.早上升旗时地面上旗杆的影子 B.上午人走在路上的影子
C.中午用来乘凉的树影 D.晚上人走在路灯下的影子
2.甲和乙两个几何体都是由大小相同的小立方块搭成,它们的俯视图如图,小正方形中数字表示该位置上的小立方块个数( )
A.甲和乙左视图相同,主视图相同 B.甲和乙左视图不相同,主视图不相同
C.甲和乙左视图相同,主视图不相同 D.甲和乙左视图不相同,主视图相同
3.一个正方形的正投影不可能是( )
A.正方形 B.矩形 C.线段 D.点
4.如图所示的几何体,其俯视图是( )
A. B.
C. D.
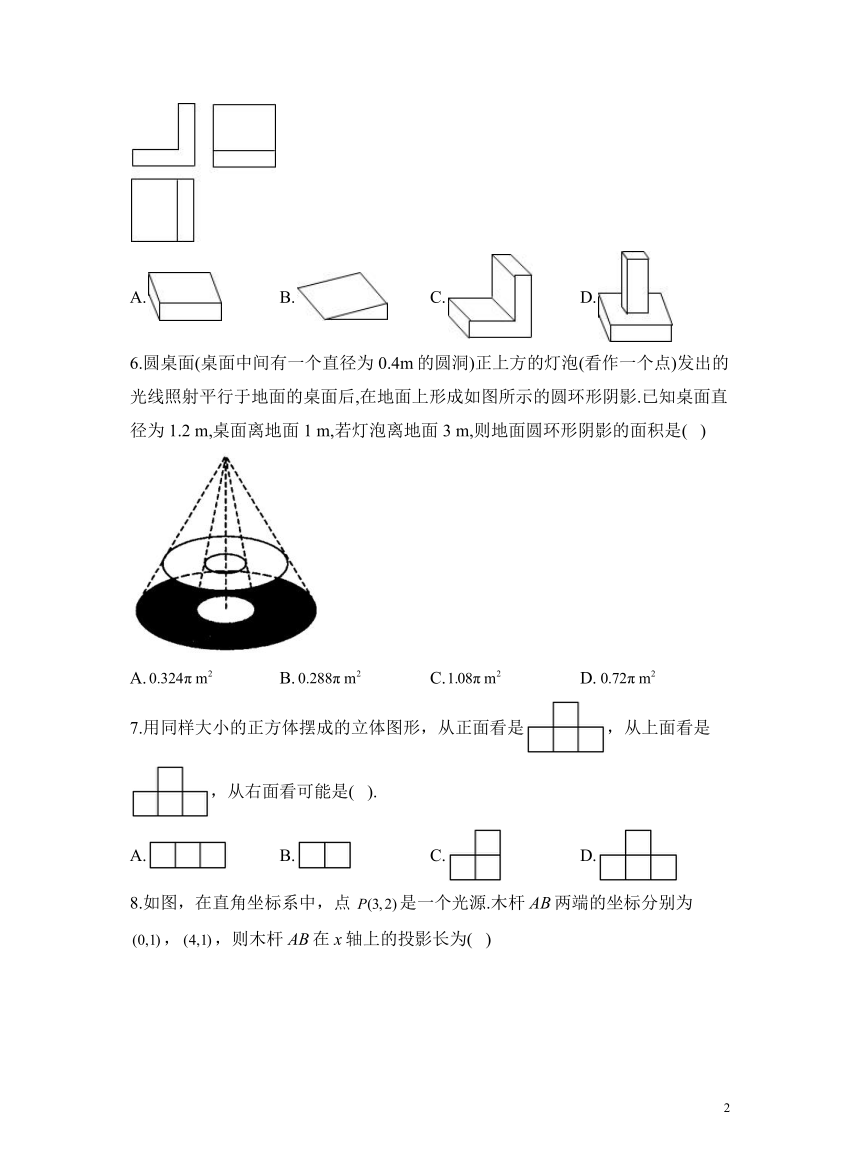
5.几何体的三视图如图所示,这个几何体是( )
A. B. C. D.
6.圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2 m,桌面离地面1 m,若灯泡离地面3 m,则地面圆环形阴影的面积是( )
A. B. C. D.
7.用同样大小的正方体摆成的立体图形,从正面看是,从上面看是,从右面看可能是( ).
A. B. C. D.
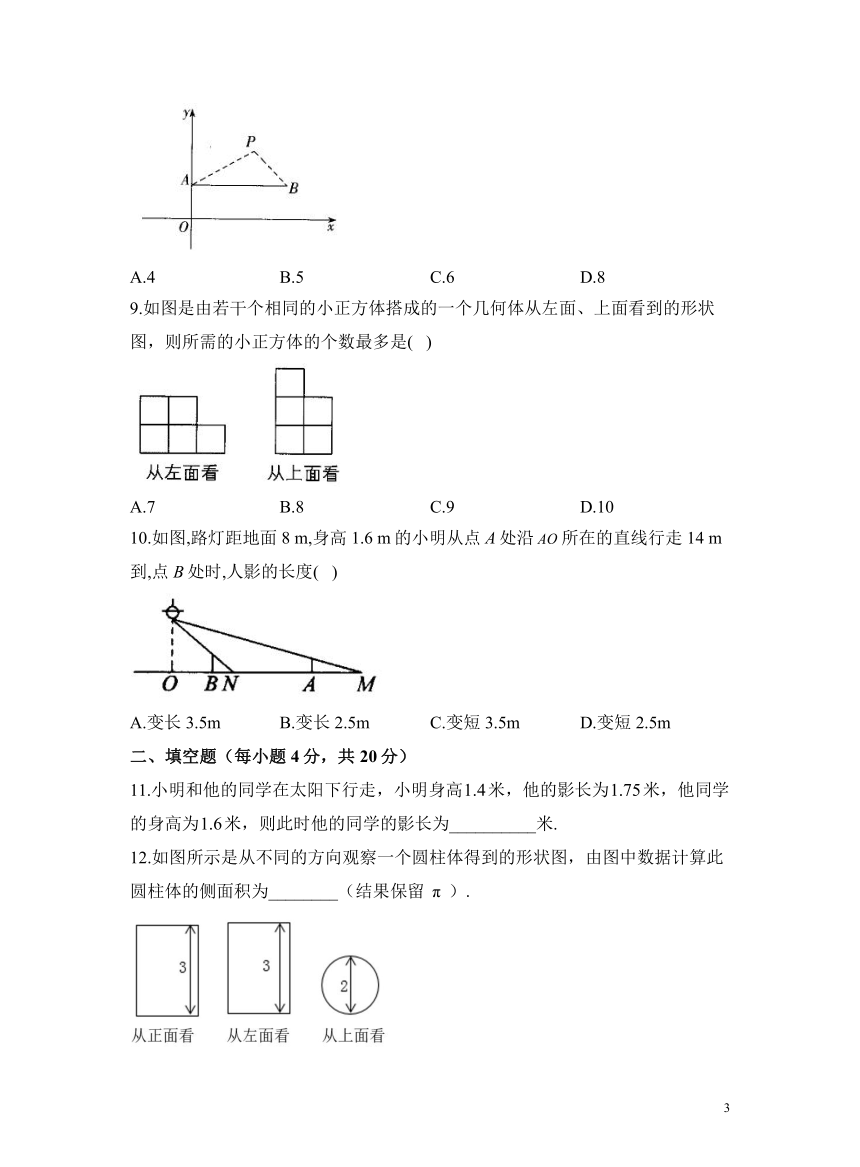
8.如图,在直角坐标系中,点是一个光源.木杆AB两端的坐标分别为,,则木杆AB在x轴上的投影长为( )
A.4 B.5 C.6 D.8
9.如图是由若干个相同的小正方体搭成的一个几何体从左面、上面看到的形状图,则所需的小正方体的个数最多是( )
A.7 B.8 C.9 D.10
10.如图,路灯距地面8 m,身高1.6 m的小明从点A处沿所在的直线行走14 m到,点B处时,人影的长度( )
A.变长3.5m B.变长2.5m C.变短3.5m D.变短2.5m
二、填空题(每小题4分,共20分)
11.小明和他的同学在太阳下行走,小明身高米,他的影长为米,他同学的身高为米,则此时他的同学的影长为__________米.
12.如图所示是从不同的方向观察一个圆柱体得到的形状图,由图中数据计算此圆柱体的侧面积为________(结果保留).
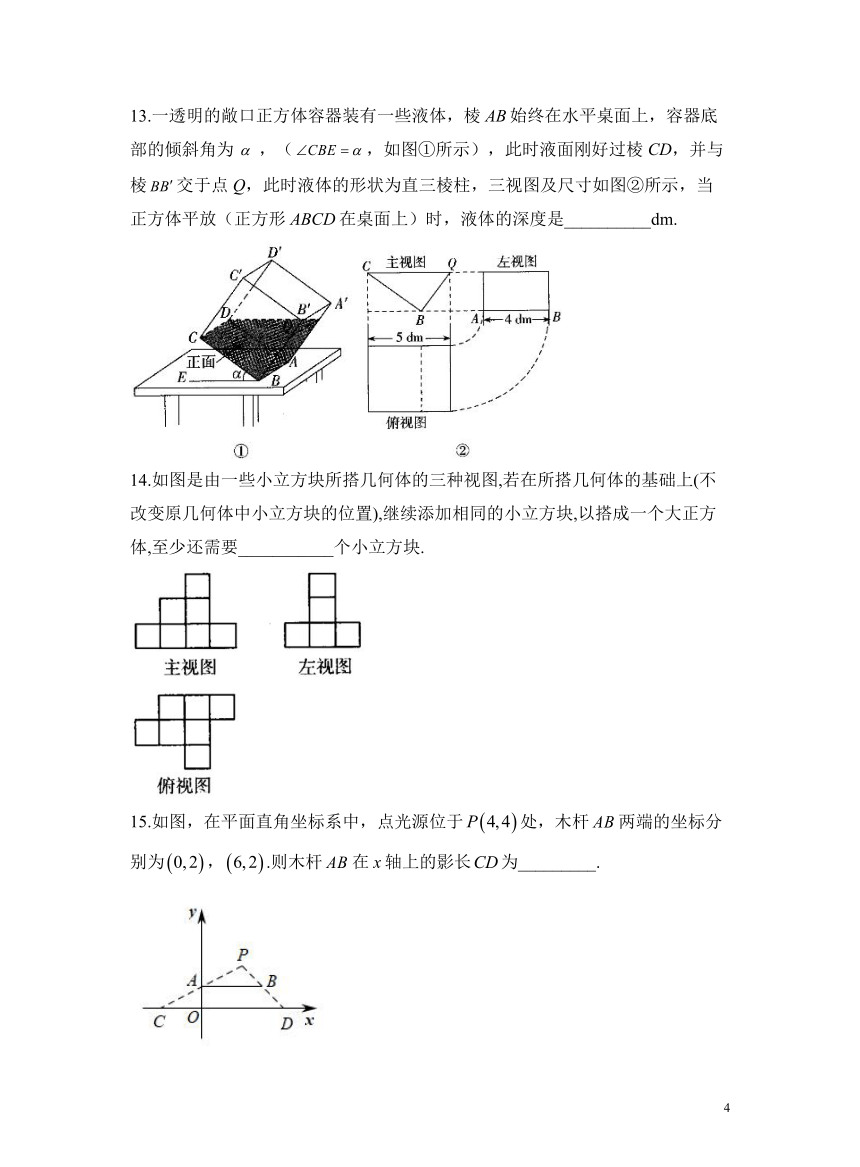
13.一透明的敞口正方体容器装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为,(,如图①所示),此时液面刚好过棱CD,并与棱交于点Q,此时液体的形状为直三棱柱,三视图及尺寸如图②所示,当正方体平放(正方形ABCD在桌面上)时,液体的深度是__________dm.
14.如图是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要___________个小立方块.
15.如图,在平面直角坐标系中,点光源位于处,木杆两端的坐标分别为,.则木杆在x轴上的影长为_________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图是一个几何体的三视图,其中俯视图为正三角形.
(1)这个几何体的名称为______.
(2)求该几何体的左视图中a的值.
17.(8分)古希腊数学家泰勒斯曾利用立杆测影的方法, 在金字塔影子的 顶部直立一根木杆, 借助太阳光测金字塔的高度. 如图, 木杆EF 长 2 米, 它的影长FD是 4 米, 同一 时刻测得OA 是 268 米,则
(1) AB与ED是否平行 _______(填“是”或“否”).
(2)金字塔的高度BO是________米.
18.(10分)为了开展趣味学习活动,张教师带领学生们在操场上利用所学的知识测量一棵树的高度如图,某一时刻树AB在太阳光照下,一部分影子NP落在了墙MN上,另一部分树影BN落在了地面上,张老师在树另一侧的地面C点放置一平面镜,在平面镜左侧点S处竖直放置了一根木杆,秦飞同学在平面镜右侧的点T处刚好可从平面镜中观察到木杆的顶端与此同时,秦飞发现木杆影子的顶端恰好落在平面镜C点处现测得木杆高2米,秦飞的眼睛距地面为1米,ST长为9米,树影NP为5米,BN为21米,求树AB的高平面镜大小忽略不计
19.(10分)如图,是由若干个完全相同的棱长为1的小正方体组成的一个几何体.
(1)请画出这个几何体的三视图;
(2)该几何体的表面积(含下底面)为;
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和左视图不变,那么最多可以再添加个小正方体.
20.(12分)如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗户距地面的高度,窗高,并测得,,求围墙AB的高度.
21.(12分)某兴趣小组开展课外活动,两地相距12米,小明从点A出发沿方向匀速前进,2秒后到达点D,此时他()在某一灯光下的影长为,继续按原速行走2秒到达点F,此时他()在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他()在同一灯光下的影长为(点在一条直线上).
(1)请在图中画出光源O点的位置,并画出位于点F时在这个灯光下的影长(不写画法);
(2)求小明原来的速度.
答案以及解析
1.答案:D
解析:中心投影的灯源为灯光,平行投影的光源为阳光与月光,
故选:D.
2.答案:D
解析:由甲俯视图知,其左视图为,由乙俯视图知,其左视图为,故它们的左 视图不相同,但它们两个的主视图相同,都是.
故选:D.
3.答案:D
解析:在同一时刻,平行物体的投影仍旧平行.得到的应是平行四边形或特殊的平行四边形.
故正方形纸的正投影不可能是点,故选D.
4.答案:C
解析:几何体的俯视图是:
故选C.
5.答案:C
解析:根据A,B,C,D三个选项的物体的主视图可知,与题图有吻合的只有C选项,故选C.
6.答案:D
解析:如图所示,,
,即,
解得.
又同理可得,
.
7.答案:C
解析:根据从上面看到的图形,可知几何体一共有两行,故排除A,D,
根据从正面看到的图形,可知几何体一共有两层,故排除A、B,
故选:C.
8.答案:D
解析:延长PA,PB分别交x轴于、,过点P作轴于E,交AB于D,如图.
的坐标为,A的坐标为,B的坐标为,
,,.
,.
,即,.故选D.
9.答案:B
解析:正方形中的数字表示该位置小正方体的个数,最多的情形如图所示,则.故选B.
10.答案:C
解析:设小明在A处时影长为长为,在B处时的影长为如图,
,
,
,
则,
,
,故人影的长度变短3.5 m.
11.答案:2
解析:设他的同学的影长为x m,
同一时刻物高与影长成比例,
,
解得,,
经检验,是原方程的解,
他的同学的影长为2 m,
故答案为:2.
12.答案:
解析:由图可知,圆柱体的底面直径为2,高为3,
所以,侧面积.
故答案为:.
13.答案:1.5
解析:由三视图可以判断,正方体的棱长.
.
液体的体积为,
当正方体平放时,液体的深度是.
14.答案:54
解析:由俯视图易得最底层有7个小立方块,第二层有2个小立方块,第三层有1个小立方块,那么共有7+2+1=10(个)小立方块组成.若搭成一个大正方体,共需4×4×4=64(个)小立方块,所以还需64-10=54(个)小立方块.
15.答案:12
解析:解:过P作轴于E,交于M,如图,
,,.
,,,
,
,
,
,
;
故答案为:12.
16.答案:(1)正三棱柱
(2)
解析:(1)略
(2)如图,过点C作于M.
是正三角形,,
,
,
左视图中a的值为.
17.答案:(1)是
(2)134
解析:(1)略
(2)由题意可知 ,, 即, 解得(米).
18.答案:12米
解析:如图所示,过点P做,再令木杆顶点为点E,秦飞的眼睛为点F,
由平面镜反射定律可知.
,
.
设,则,.
,
解得.
又由太阳光线同时刻平行得,
,即,
,
,
米,
答:树AB的高为12米.
19.解析:(1)如图所示:
(2)
故答案为:28.
(3)由分析可知,最多可以再添加2个小正方体,如图,
故答案为:2
20.答案:如图,连接CD,由题意知O、D、C在一条直线上.
,.,,.
,,.
设,,,.
.,即.
解得.
经检验是原分式方程的解,且符合题意.
答:围墙AB的高度是4.4 m.
21.答案:(1)
(2)1.5米/秒
解析: (1)延长相交于点O,延长交于点M,如图,则点即为所作.
(2)设小明原来的速度为x米/秒,
则米,米,
米,米.
,
,
,
,即,
,
解得(不合题意,舍去).
经检验,是原方程的解,
∴小明原来的速度为1.5米/秒.
1
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.下列各种现象属于中心投影现象的是( )
A.早上升旗时地面上旗杆的影子 B.上午人走在路上的影子
C.中午用来乘凉的树影 D.晚上人走在路灯下的影子
2.甲和乙两个几何体都是由大小相同的小立方块搭成,它们的俯视图如图,小正方形中数字表示该位置上的小立方块个数( )
A.甲和乙左视图相同,主视图相同 B.甲和乙左视图不相同,主视图不相同
C.甲和乙左视图相同,主视图不相同 D.甲和乙左视图不相同,主视图相同
3.一个正方形的正投影不可能是( )
A.正方形 B.矩形 C.线段 D.点
4.如图所示的几何体,其俯视图是( )
A. B.
C. D.
5.几何体的三视图如图所示,这个几何体是( )
A. B. C. D.
6.圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2 m,桌面离地面1 m,若灯泡离地面3 m,则地面圆环形阴影的面积是( )
A. B. C. D.
7.用同样大小的正方体摆成的立体图形,从正面看是,从上面看是,从右面看可能是( ).
A. B. C. D.
8.如图,在直角坐标系中,点是一个光源.木杆AB两端的坐标分别为,,则木杆AB在x轴上的投影长为( )
A.4 B.5 C.6 D.8
9.如图是由若干个相同的小正方体搭成的一个几何体从左面、上面看到的形状图,则所需的小正方体的个数最多是( )
A.7 B.8 C.9 D.10
10.如图,路灯距地面8 m,身高1.6 m的小明从点A处沿所在的直线行走14 m到,点B处时,人影的长度( )
A.变长3.5m B.变长2.5m C.变短3.5m D.变短2.5m
二、填空题(每小题4分,共20分)
11.小明和他的同学在太阳下行走,小明身高米,他的影长为米,他同学的身高为米,则此时他的同学的影长为__________米.
12.如图所示是从不同的方向观察一个圆柱体得到的形状图,由图中数据计算此圆柱体的侧面积为________(结果保留).
13.一透明的敞口正方体容器装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为,(,如图①所示),此时液面刚好过棱CD,并与棱交于点Q,此时液体的形状为直三棱柱,三视图及尺寸如图②所示,当正方体平放(正方形ABCD在桌面上)时,液体的深度是__________dm.
14.如图是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要___________个小立方块.
15.如图,在平面直角坐标系中,点光源位于处,木杆两端的坐标分别为,.则木杆在x轴上的影长为_________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图是一个几何体的三视图,其中俯视图为正三角形.
(1)这个几何体的名称为______.
(2)求该几何体的左视图中a的值.
17.(8分)古希腊数学家泰勒斯曾利用立杆测影的方法, 在金字塔影子的 顶部直立一根木杆, 借助太阳光测金字塔的高度. 如图, 木杆EF 长 2 米, 它的影长FD是 4 米, 同一 时刻测得OA 是 268 米,则
(1) AB与ED是否平行 _______(填“是”或“否”).
(2)金字塔的高度BO是________米.
18.(10分)为了开展趣味学习活动,张教师带领学生们在操场上利用所学的知识测量一棵树的高度如图,某一时刻树AB在太阳光照下,一部分影子NP落在了墙MN上,另一部分树影BN落在了地面上,张老师在树另一侧的地面C点放置一平面镜,在平面镜左侧点S处竖直放置了一根木杆,秦飞同学在平面镜右侧的点T处刚好可从平面镜中观察到木杆的顶端与此同时,秦飞发现木杆影子的顶端恰好落在平面镜C点处现测得木杆高2米,秦飞的眼睛距地面为1米,ST长为9米,树影NP为5米,BN为21米,求树AB的高平面镜大小忽略不计
19.(10分)如图,是由若干个完全相同的棱长为1的小正方体组成的一个几何体.
(1)请画出这个几何体的三视图;
(2)该几何体的表面积(含下底面)为;
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和左视图不变,那么最多可以再添加个小正方体.
20.(12分)如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗户距地面的高度,窗高,并测得,,求围墙AB的高度.
21.(12分)某兴趣小组开展课外活动,两地相距12米,小明从点A出发沿方向匀速前进,2秒后到达点D,此时他()在某一灯光下的影长为,继续按原速行走2秒到达点F,此时他()在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他()在同一灯光下的影长为(点在一条直线上).
(1)请在图中画出光源O点的位置,并画出位于点F时在这个灯光下的影长(不写画法);
(2)求小明原来的速度.
答案以及解析
1.答案:D
解析:中心投影的灯源为灯光,平行投影的光源为阳光与月光,
故选:D.
2.答案:D
解析:由甲俯视图知,其左视图为,由乙俯视图知,其左视图为,故它们的左 视图不相同,但它们两个的主视图相同,都是.
故选:D.
3.答案:D
解析:在同一时刻,平行物体的投影仍旧平行.得到的应是平行四边形或特殊的平行四边形.
故正方形纸的正投影不可能是点,故选D.
4.答案:C
解析:几何体的俯视图是:
故选C.
5.答案:C
解析:根据A,B,C,D三个选项的物体的主视图可知,与题图有吻合的只有C选项,故选C.
6.答案:D
解析:如图所示,,
,即,
解得.
又同理可得,
.
7.答案:C
解析:根据从上面看到的图形,可知几何体一共有两行,故排除A,D,
根据从正面看到的图形,可知几何体一共有两层,故排除A、B,
故选:C.
8.答案:D
解析:延长PA,PB分别交x轴于、,过点P作轴于E,交AB于D,如图.
的坐标为,A的坐标为,B的坐标为,
,,.
,.
,即,.故选D.
9.答案:B
解析:正方形中的数字表示该位置小正方体的个数,最多的情形如图所示,则.故选B.
10.答案:C
解析:设小明在A处时影长为长为,在B处时的影长为如图,
,
,
,
则,
,
,故人影的长度变短3.5 m.
11.答案:2
解析:设他的同学的影长为x m,
同一时刻物高与影长成比例,
,
解得,,
经检验,是原方程的解,
他的同学的影长为2 m,
故答案为:2.
12.答案:
解析:由图可知,圆柱体的底面直径为2,高为3,
所以,侧面积.
故答案为:.
13.答案:1.5
解析:由三视图可以判断,正方体的棱长.
.
液体的体积为,
当正方体平放时,液体的深度是.
14.答案:54
解析:由俯视图易得最底层有7个小立方块,第二层有2个小立方块,第三层有1个小立方块,那么共有7+2+1=10(个)小立方块组成.若搭成一个大正方体,共需4×4×4=64(个)小立方块,所以还需64-10=54(个)小立方块.
15.答案:12
解析:解:过P作轴于E,交于M,如图,
,,.
,,,
,
,
,
,
;
故答案为:12.
16.答案:(1)正三棱柱
(2)
解析:(1)略
(2)如图,过点C作于M.
是正三角形,,
,
,
左视图中a的值为.
17.答案:(1)是
(2)134
解析:(1)略
(2)由题意可知 ,, 即, 解得(米).
18.答案:12米
解析:如图所示,过点P做,再令木杆顶点为点E,秦飞的眼睛为点F,
由平面镜反射定律可知.
,
.
设,则,.
,
解得.
又由太阳光线同时刻平行得,
,即,
,
,
米,
答:树AB的高为12米.
19.解析:(1)如图所示:
(2)
故答案为:28.
(3)由分析可知,最多可以再添加2个小正方体,如图,
故答案为:2
20.答案:如图,连接CD,由题意知O、D、C在一条直线上.
,.,,.
,,.
设,,,.
.,即.
解得.
经检验是原分式方程的解,且符合题意.
答:围墙AB的高度是4.4 m.
21.答案:(1)
(2)1.5米/秒
解析: (1)延长相交于点O,延长交于点M,如图,则点即为所作.
(2)设小明原来的速度为x米/秒,
则米,米,
米,米.
,
,
,
,即,
,
解得(不合题意,舍去).
经检验,是原方程的解,
∴小明原来的速度为1.5米/秒.
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
