第二章 实数(测能力)(含解析)——2023-2024学年北师大版数学八年级上册单元闯关双测卷
文档属性
| 名称 | 第二章 实数(测能力)(含解析)——2023-2024学年北师大版数学八年级上册单元闯关双测卷 |  | |
| 格式 | docx | ||
| 文件大小 | 649.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 22:33:30 | ||
图片预览



文档简介
第二章 实数(测能力)——2023-2024学年北师大版数学八年级上册单元闯关双测卷
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.有下列各数:0,,0.3131131113…(相邻两个3之间1的个数逐次增加1),,,,3.14,其中无理数的个数为( )
A.1 B.2 C.3 D.4
2.对于所有实数a,b,下列等式从左到右一定成立的是( )
A. B. C. D.
3.下列计算正确的是( )
A. B. C. D.
4.某校要举办国庆联欢会,主持人站在舞台中轴线AB的黄金分割点C处(如图1)最自然得体.即,在数轴(如题图2)上最接近的点是( )
A.P B.Q C.M D.N
5.实数a在数轴上的位置如图所示,则化简后为( )
A.9 B. C. D.
6.下列说法正确的有几个( )
①两个无理数的和可能是有理数;
②任意一个无理数都可以用数轴上的点表示;
③一定没有平方根;
④实数包括有理数、无理数和零;
⑤立方根等于本身的数是1.
A.1个 B.2个 C.3个 D.4个
7.已知,,,则下列大小关系正确的是( )
A. B. C. D.
8.若2022的两个平方根是m和n,则的值是( )
A.0 B.2022 C. D.4044
9.在一个正方形的内部按照如图方式放置大小不同的两个小正方形,其中较大的正方形面积为12,重叠部分的面积为3,空白部分的面积为,则较小的正方形面积为( )
A.11 B.10 C.9 D.8
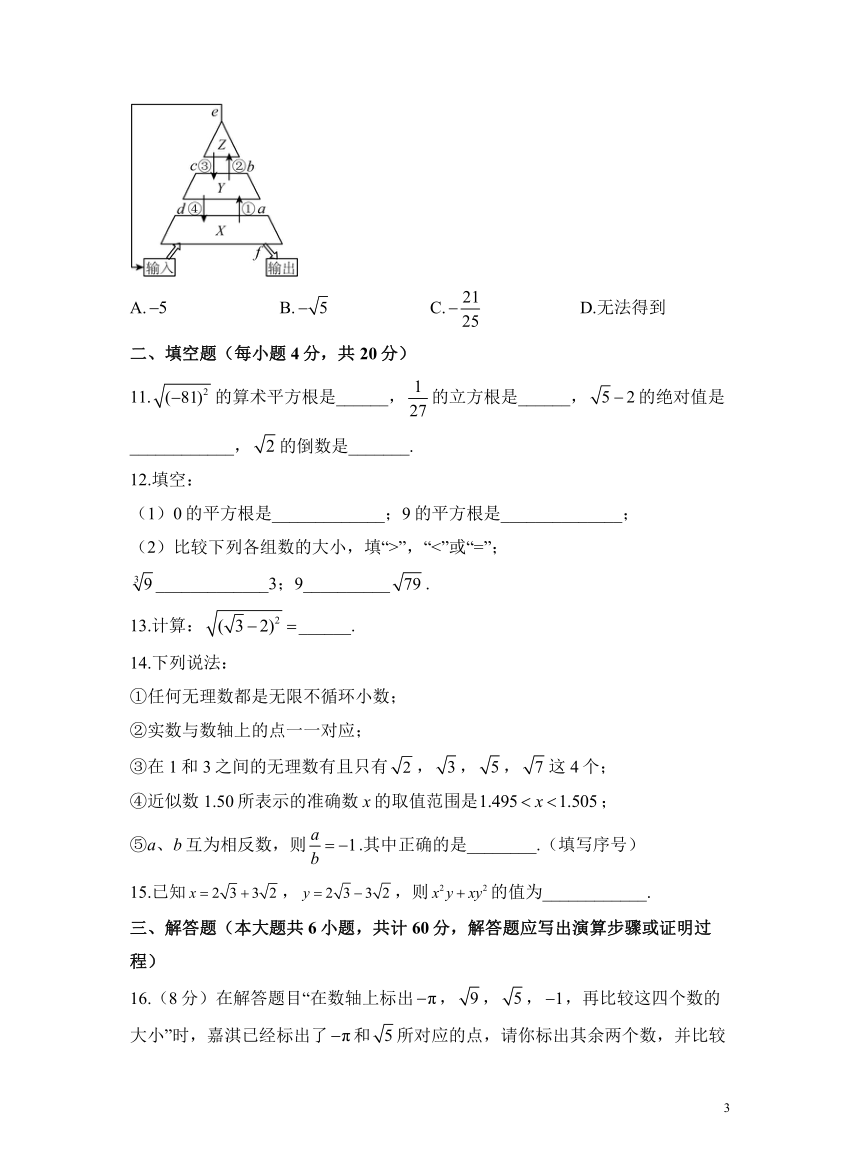
10.如图所示为一金字塔运算程序,其中箭头为数字的移动方向,字母表示限制条件,序号为运算方式,已知a:;
①:;b:;
②:;c:;
③:;d:;
④:;e:;f:,
若某层中的数字达到限制条件,就可以通过相应的运算方式进入新一层,安安将输入的数字定为2,则最后输出的结果为( )
A. B. C. D.无法得到
二、填空题(每小题4分,共20分)
11.的算术平方根是______,的立方根是______,的绝对值是____________,的倒数是_______.
12.填空:
(1)0的平方根是_____________;9的平方根是______________;
(2)比较下列各组数的大小,填“>”,“<”或“=”;
_____________3;9__________.
13.计算:______.
14.下列说法:
①任何无理数都是无限不循环小数;
②实数与数轴上的点一一对应;
③在1和3之间的无理数有且只有,,,这4个;
④近似数1.50所表示的准确数x的取值范围是;
⑤a、b互为相反数,则.其中正确的是________.(填写序号)
15.已知,,则的值为____________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)在解答题目“在数轴上标出,,,,再比较这四个数的大小”时,嘉淇已经标出了和所对应的点,请你标出其余两个数,并比较这四个数的大小.
17.(8分)阅读下面的文字,解答问题:
大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:,即,的整数部分为2,小数部分为.
请解答:
(1)的整数部分是__________,小数部分是__________.
(2)如果的小数部分为a,的整数部分为b,求的值;
18.(10分)已知a满足,b满足,若.
(1)求m的立方根;
(2)若,求n的值.
19.(10分)【阅读材料】像,,两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如,与,与,与等都是互为有理化因式.进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
【解决问题】
(1)填空:的有理化因式为________;
(2)化简:;
(3)已知正整数a,b满足,求a,b的值.
20.(12分)观察下列规律回答问题:,,,,,….
(1)则________;__________;按上述规律,已知数a小数点的移动与它的立方根的小数点移动间有何规律?
(2)已知,若,用含x的代数式表示y,则_________;
(3)根据规律写出与a的大小情况.
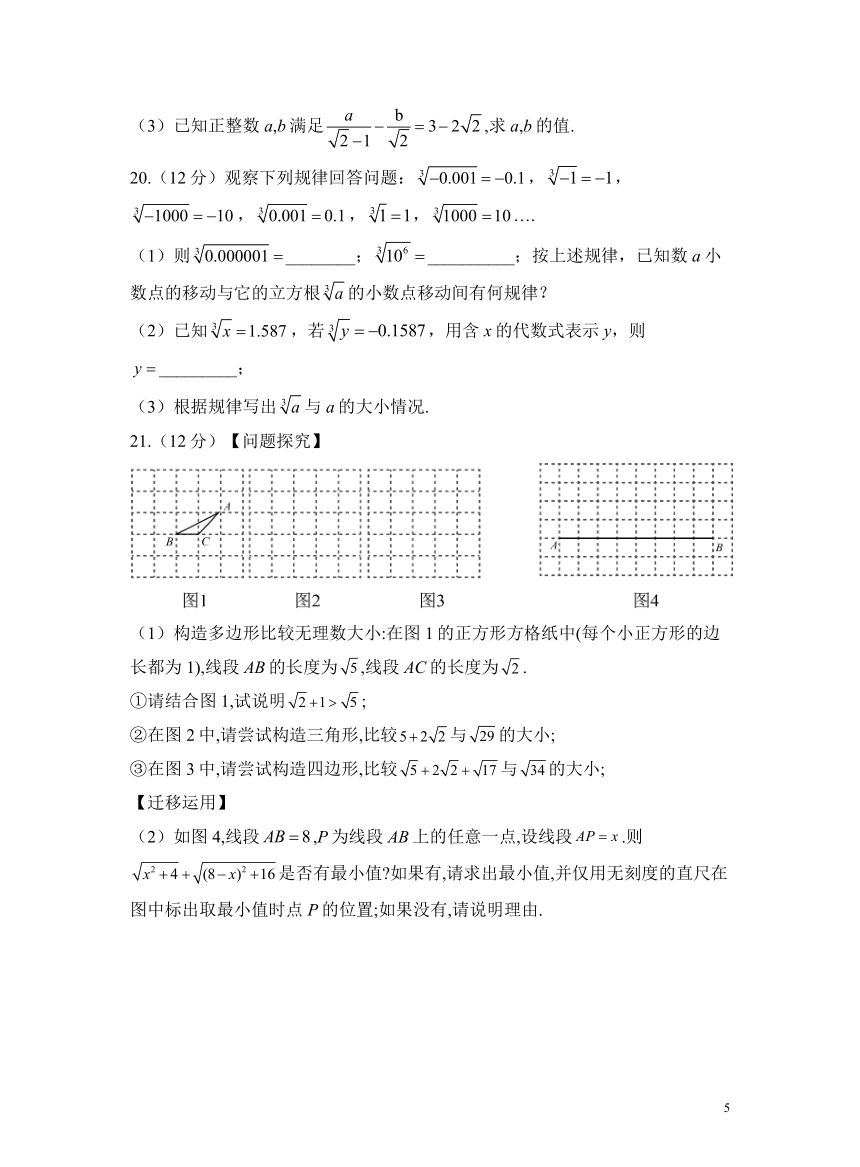
21.(12分)【问题探究】
(1)构造多边形比较无理数大小:在图1的正方形方格纸中(每个小正方形的边长都为1),线段AB的长度为,线段AC的长度为.
①请结合图1,试说明;
②在图2中,请尝试构造三角形,比较与的大小;
③在图3中,请尝试构造四边形,比较与的大小;
【迁移运用】
(2)如图4,线段,P为线段AB上的任意一点,设线段.则是否有最小值 如果有,请求出最小值,并仅用无刻度的直尺在图中标出取最小值时点P的位置;如果没有,请说明理由.
答案以及解析
1.答案:B
解析:在0,,0.3131131113…(相邻两个3之间1的个数逐次增加1),,,,3.14中,无理数有0.3131131113…(相邻两个3之间1的个数逐次增加1),,共2个;
故选B.
2.答案:D
解析:当时,,当时,,故A不一定成立;
当a,b都小于0时,,故B不一定成立;
,故C不成立;
,故D成立,
故选:D.
3.答案:C
解析:A、,本选项不符合题意;
B、,本选项不符合题意;
C、,本选项符合题意;
D、,本选项不符合题意;
故选:C.
4.答案:C
解析:,
,
而点M对应的数在0和1之间,
所以,最接近的点是M,
故选:C.
5.答案:A
解析:,
原式
.
故选:A.
6.答案:B
解析:①两个无理数的和可能是有理数,正确;
②任意一个无理数都可以用数轴上的点表示,正确;
③当时,有平方根,故原说法错误;
④实数包括有理数、无理数,故原说法错误;
⑤立方根等于本身的数是和0,故原说法错误;
综上,说法正确的有①②,共2个.
故选:B.
7.答案:A
解析:,.,..故选A.
8.答案:C
解析:2022的两个平方根是m和n,
,,
,
故选:C
9.答案:B
解析:观察可知,两个空白部分的长相等,宽也相等,
重叠部分也为正方形,
空白部分的面积为,
一个空白长方形面积,
大正方形面积为12,重叠部分面积为3,
大正方形边长,重叠部分边长,
空白部分的长,
设空白部分宽为x,可得:,解得:,
小正方形的边长=空白部分的宽+阴影部分边长,
小正方形面积,
故选:B.
10.答案:D
解析:输入是数字是,符合条件a:,进入第二层,
由①得,则,符合条件b:,进入第三层,
由②得,,符合条件e:,回到第一层,
第二次输入的数字是,符合条件a:,进入第二层,
则,符合条件b:,进入第三层
由②得,,符合条件c:,返回第二层,
由③得,,,进入第三层
由②得,,符合条件c:,返回第二层,
由③得,,,进入第三层
由②得,,符合条件c:,返回第二层,
由③得,,,进入第三层
……
观察发现,数字越来越大,在第二、三层循环,
故选:D.
11.答案:9,,,
解析:
的算术平方根为9;
的立方根为;
,
的绝对值是,
的倒数是.
故答案为9,, ,.
12.答案:(1)0;
(2)<;>
解析:(1)0的平方根是0;9的平方根是;
故答案为:0;;
(2),,
,,
故答案为:<;>.
13.答案:
解析:原式
.
故答案为.
14.答案:①②
解析:①任何无理数都是无限不循环小数,说法正确;
②实数与数轴上的点一一对应,说法正确;
③在1和3之间的无理数有无数个,原说法错误;
④近似数1.50所表示的准确数x的取值范围是,原说法错误;
⑤a、b互为相反数,当时,无意义,原说法错误;
综上,正确的是:①②;
故答案为:①②.
15.答案:
解析:因为,,所以,,所以.
16.答案:,数轴见解析
解析:,
,
结合,,可知,在数轴上如下图所示:
由,,,在数轴上的位置可知:.
17.(1)答案:3;
解析:的整数部分是3,
小数部分是:;
(2)答案:4
解析:,
的小数部分为:,
,
的整数部分为:,
.
18.答案:(1)4
(2)51
解析:(1),
,
,
,解得:,
把,代入得:,
m的立方根是;
(2)由(1)可得:,
,
,
,
解得:.
19.答案:(1)
(2)
(3)10
解析:(1)的有理化因式为;
(2)原式;
(3)原式可化为,
,
,
,,
.
20.答案:(1)、
(2)
(3)当或时,;当或时,;当或时,
解析:(1);;
按上述规律,被开方数小数点向右(或左)移三位,则所得数的小数点向右(或左)移一位,
故答案为:、;
(2)由(1)中规律可得,已知,若,
则y的绝对值是x的且符号相反;
用含x的代数式表示y,则,
故答案为:;
(3),,,,,
与a的大小情况为:
当或时,;
当或时,;
当或时,.
21.答案:(1)①见解析;
②图见解析,;
③图见解析,
(2)有最小值,最小值为10
解析:(1)①在图1的正方形方格纸中(每个小正方形的边长都为),线段AB的长度为,线段AC的长度为.
故在中,,即;
②如图:在正方形方格纸中构建,,,
故在中,,即;
③如图:在正方形方格纸中构建,,,,连接BD,
故在中,,则,
在中,,故,
即;
(2)有最小值;
理由如下:设,则,如图:
,
当C,P,D三点共线时,的值最小,
的最小值,
即的最小值为10.
1
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.有下列各数:0,,0.3131131113…(相邻两个3之间1的个数逐次增加1),,,,3.14,其中无理数的个数为( )
A.1 B.2 C.3 D.4
2.对于所有实数a,b,下列等式从左到右一定成立的是( )
A. B. C. D.
3.下列计算正确的是( )
A. B. C. D.
4.某校要举办国庆联欢会,主持人站在舞台中轴线AB的黄金分割点C处(如图1)最自然得体.即,在数轴(如题图2)上最接近的点是( )
A.P B.Q C.M D.N
5.实数a在数轴上的位置如图所示,则化简后为( )
A.9 B. C. D.
6.下列说法正确的有几个( )
①两个无理数的和可能是有理数;
②任意一个无理数都可以用数轴上的点表示;
③一定没有平方根;
④实数包括有理数、无理数和零;
⑤立方根等于本身的数是1.
A.1个 B.2个 C.3个 D.4个
7.已知,,,则下列大小关系正确的是( )
A. B. C. D.
8.若2022的两个平方根是m和n,则的值是( )
A.0 B.2022 C. D.4044
9.在一个正方形的内部按照如图方式放置大小不同的两个小正方形,其中较大的正方形面积为12,重叠部分的面积为3,空白部分的面积为,则较小的正方形面积为( )
A.11 B.10 C.9 D.8
10.如图所示为一金字塔运算程序,其中箭头为数字的移动方向,字母表示限制条件,序号为运算方式,已知a:;
①:;b:;
②:;c:;
③:;d:;
④:;e:;f:,
若某层中的数字达到限制条件,就可以通过相应的运算方式进入新一层,安安将输入的数字定为2,则最后输出的结果为( )
A. B. C. D.无法得到
二、填空题(每小题4分,共20分)
11.的算术平方根是______,的立方根是______,的绝对值是____________,的倒数是_______.
12.填空:
(1)0的平方根是_____________;9的平方根是______________;
(2)比较下列各组数的大小,填“>”,“<”或“=”;
_____________3;9__________.
13.计算:______.
14.下列说法:
①任何无理数都是无限不循环小数;
②实数与数轴上的点一一对应;
③在1和3之间的无理数有且只有,,,这4个;
④近似数1.50所表示的准确数x的取值范围是;
⑤a、b互为相反数,则.其中正确的是________.(填写序号)
15.已知,,则的值为____________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)在解答题目“在数轴上标出,,,,再比较这四个数的大小”时,嘉淇已经标出了和所对应的点,请你标出其余两个数,并比较这四个数的大小.
17.(8分)阅读下面的文字,解答问题:
大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:,即,的整数部分为2,小数部分为.
请解答:
(1)的整数部分是__________,小数部分是__________.
(2)如果的小数部分为a,的整数部分为b,求的值;
18.(10分)已知a满足,b满足,若.
(1)求m的立方根;
(2)若,求n的值.
19.(10分)【阅读材料】像,,两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如,与,与,与等都是互为有理化因式.进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
【解决问题】
(1)填空:的有理化因式为________;
(2)化简:;
(3)已知正整数a,b满足,求a,b的值.
20.(12分)观察下列规律回答问题:,,,,,….
(1)则________;__________;按上述规律,已知数a小数点的移动与它的立方根的小数点移动间有何规律?
(2)已知,若,用含x的代数式表示y,则_________;
(3)根据规律写出与a的大小情况.
21.(12分)【问题探究】
(1)构造多边形比较无理数大小:在图1的正方形方格纸中(每个小正方形的边长都为1),线段AB的长度为,线段AC的长度为.
①请结合图1,试说明;
②在图2中,请尝试构造三角形,比较与的大小;
③在图3中,请尝试构造四边形,比较与的大小;
【迁移运用】
(2)如图4,线段,P为线段AB上的任意一点,设线段.则是否有最小值 如果有,请求出最小值,并仅用无刻度的直尺在图中标出取最小值时点P的位置;如果没有,请说明理由.
答案以及解析
1.答案:B
解析:在0,,0.3131131113…(相邻两个3之间1的个数逐次增加1),,,,3.14中,无理数有0.3131131113…(相邻两个3之间1的个数逐次增加1),,共2个;
故选B.
2.答案:D
解析:当时,,当时,,故A不一定成立;
当a,b都小于0时,,故B不一定成立;
,故C不成立;
,故D成立,
故选:D.
3.答案:C
解析:A、,本选项不符合题意;
B、,本选项不符合题意;
C、,本选项符合题意;
D、,本选项不符合题意;
故选:C.
4.答案:C
解析:,
,
而点M对应的数在0和1之间,
所以,最接近的点是M,
故选:C.
5.答案:A
解析:,
原式
.
故选:A.
6.答案:B
解析:①两个无理数的和可能是有理数,正确;
②任意一个无理数都可以用数轴上的点表示,正确;
③当时,有平方根,故原说法错误;
④实数包括有理数、无理数,故原说法错误;
⑤立方根等于本身的数是和0,故原说法错误;
综上,说法正确的有①②,共2个.
故选:B.
7.答案:A
解析:,.,..故选A.
8.答案:C
解析:2022的两个平方根是m和n,
,,
,
故选:C
9.答案:B
解析:观察可知,两个空白部分的长相等,宽也相等,
重叠部分也为正方形,
空白部分的面积为,
一个空白长方形面积,
大正方形面积为12,重叠部分面积为3,
大正方形边长,重叠部分边长,
空白部分的长,
设空白部分宽为x,可得:,解得:,
小正方形的边长=空白部分的宽+阴影部分边长,
小正方形面积,
故选:B.
10.答案:D
解析:输入是数字是,符合条件a:,进入第二层,
由①得,则,符合条件b:,进入第三层,
由②得,,符合条件e:,回到第一层,
第二次输入的数字是,符合条件a:,进入第二层,
则,符合条件b:,进入第三层
由②得,,符合条件c:,返回第二层,
由③得,,,进入第三层
由②得,,符合条件c:,返回第二层,
由③得,,,进入第三层
由②得,,符合条件c:,返回第二层,
由③得,,,进入第三层
……
观察发现,数字越来越大,在第二、三层循环,
故选:D.
11.答案:9,,,
解析:
的算术平方根为9;
的立方根为;
,
的绝对值是,
的倒数是.
故答案为9,, ,.
12.答案:(1)0;
(2)<;>
解析:(1)0的平方根是0;9的平方根是;
故答案为:0;;
(2),,
,,
故答案为:<;>.
13.答案:
解析:原式
.
故答案为.
14.答案:①②
解析:①任何无理数都是无限不循环小数,说法正确;
②实数与数轴上的点一一对应,说法正确;
③在1和3之间的无理数有无数个,原说法错误;
④近似数1.50所表示的准确数x的取值范围是,原说法错误;
⑤a、b互为相反数,当时,无意义,原说法错误;
综上,正确的是:①②;
故答案为:①②.
15.答案:
解析:因为,,所以,,所以.
16.答案:,数轴见解析
解析:,
,
结合,,可知,在数轴上如下图所示:
由,,,在数轴上的位置可知:.
17.(1)答案:3;
解析:的整数部分是3,
小数部分是:;
(2)答案:4
解析:,
的小数部分为:,
,
的整数部分为:,
.
18.答案:(1)4
(2)51
解析:(1),
,
,
,解得:,
把,代入得:,
m的立方根是;
(2)由(1)可得:,
,
,
,
解得:.
19.答案:(1)
(2)
(3)10
解析:(1)的有理化因式为;
(2)原式;
(3)原式可化为,
,
,
,,
.
20.答案:(1)、
(2)
(3)当或时,;当或时,;当或时,
解析:(1);;
按上述规律,被开方数小数点向右(或左)移三位,则所得数的小数点向右(或左)移一位,
故答案为:、;
(2)由(1)中规律可得,已知,若,
则y的绝对值是x的且符号相反;
用含x的代数式表示y,则,
故答案为:;
(3),,,,,
与a的大小情况为:
当或时,;
当或时,;
当或时,.
21.答案:(1)①见解析;
②图见解析,;
③图见解析,
(2)有最小值,最小值为10
解析:(1)①在图1的正方形方格纸中(每个小正方形的边长都为),线段AB的长度为,线段AC的长度为.
故在中,,即;
②如图:在正方形方格纸中构建,,,
故在中,,即;
③如图:在正方形方格纸中构建,,,,连接BD,
故在中,,则,
在中,,故,
即;
(2)有最小值;
理由如下:设,则,如图:
,
当C,P,D三点共线时,的值最小,
的最小值,
即的最小值为10.
1
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
