第二章 一元二次方程(测能力)(含解析)——2023-2024学年北师大版数学九年级上册单元闯关双测卷
文档属性
| 名称 | 第二章 一元二次方程(测能力)(含解析)——2023-2024学年北师大版数学九年级上册单元闯关双测卷 |  | |
| 格式 | docx | ||
| 文件大小 | 551.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 22:34:35 | ||
图片预览




文档简介
第二章 一元二次方程(测能力)——2023-2024学年北师大版数学九年级上册单元闯关双测卷
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.若关于x的一元二次方程的常数项为0,则a的值等于( )
A.1 B.2 C.1或2 D.0
2.用配方法解方程的过程中,应将此方程化为( )
A. B. C. D.
3.方程的根为( )
A., B., C. D.
4.若,则一元二次方程必有一根是( )
A.0 B.无法确定 C.-2 D.2
5.如图,在中,,cm,cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从顶点C出发,沿线段CB向点B方向运动,如果点P的速度是2cm/s,点Q的速度是1cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动,当P,Q两点运动( )秒时,的面积等于.
A.1 B.3 C.3或5 D.1或5
6.新定义,若关于x的一元二次方程:与,称为“同族二次方程”.如与是“同族二次方程”.现有关于x的一元二次方程:与是“同族二次方程”.那么代数式能取的最小值是( )
A.2015 B.2017 C.2022 D.2027
7.已知是关于x的方程的实数根.下列说法:
①此方程有两个不相等的实数根;
②当时,一定有;
③b是此方程的根;
④此方程有两个相等的实数根.上述说法中,正确的有( )
A.①② B.②③ C.①③ D.③④
8.若关于x的一元二次方程的两根分别为,1,则关于x的一元二次方程的两根分别为( )
A., B.,
C., D.,
9.甲、乙两人同驾一辆车出游,各匀速驾驶一半路程,共用3小时,到达目的地后,甲对乙说:“我用你所花的时间,可以行驶”乙对甲说:“我用你所花的时间,只能行驶”.从他们的交谈中可以判断,乙驾车的时长为( )
A.1.2小时 B.1.6小时 C.1.8小时 D.2小时
10.若关于x的一元二次方程有两个实数根,,且,则( )
A.2或6 B.2或8 C.2 D.6
二、填空题(每小题4分,共20分)
11.网上流行一个游戏,发起游戏的人首先发出一个“祝福”链接,将这个“祝福”链接发给n个人,收到链接的人也需把链接发给相同数量的新人,经过两轮传播后,共有91人参与了这个“祝福”链接的传播,则n的值为________.
12.已知,则的值等于________.
13.在2022年7月的日历表上用一个方框圈出4个数(如图所示),若圈出的4个数中,最小数与最大数的乘积为180,则这个最小数为__________.
14.如图,数轴上点A代表的数为,点B代表的数为,已知,且点A在数轴的负半轴上,则x的值为__________.
15.如图,正方形ABCD和正方形EFGH分别由两张相同的长方形纸片无缝拼接而成,现将其摆放在桌面上,如图所示,重合部分为甲、乙、丙,其中乙为正方形,记甲、丙的面积分别为,,若,且桌面被所有纸片覆盖区域的面积为,则乙的面积为_______________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)关于x的一元二次方程有实数根.
(1)求k的取值范围:
(2)如果k是符合条件的最大整数,且一元二次方程与方程有一个相同的根,求此时m的值.
17.(8分)新学期开始时.某校九年级一班的同学为了增添教室绿色文化,准备到一家植物种植基地购买A,B两种花苗,据了解,购买A种花苗3盆,B种花苗5盆,需210元;购买A种花苗4盆,B种花苗10盆,需380元.
(1)求A,B两种花苗的单价分别是多少元;
(2)经九年级一班班委会商定,决定购买A,B两种花苗共12盆进行搭配装扮教室.种植基地销售人员为了支持本次活动,为该班同学提供以下优惠:购买多少盆B种花苗,B种花苗每盆就降价多少元.若九年级一班的同学本次购买花苗共花费了256元,请计算出本次购买了A,B两种花苗各多少盆.
18.(10分)用适当的方法解下列方程:
(1);
(2);
(3).
19.(10分)已知关于x的一元二次方程.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为,,且满足,求实数m的值.
20.(12分)某淘宝网店销售台灯,成本为每个30元.销售大数据分析表明:当每个台灯售价为40元时,平均每月售出600个;若售价每下降1元,其月销售量就增加200个.
(1)若售价下降1元,每月能售出_______个台灯,若售价下降x元(),每月能售出____个台灯.
(2)为迎接“双十一”,该网店决定降价促销,在库存为1210个台灯的情况下,若预计月获利恰好为8400元,求每个台灯的售价.
(3)月获利能否达到9600元,说明理由.
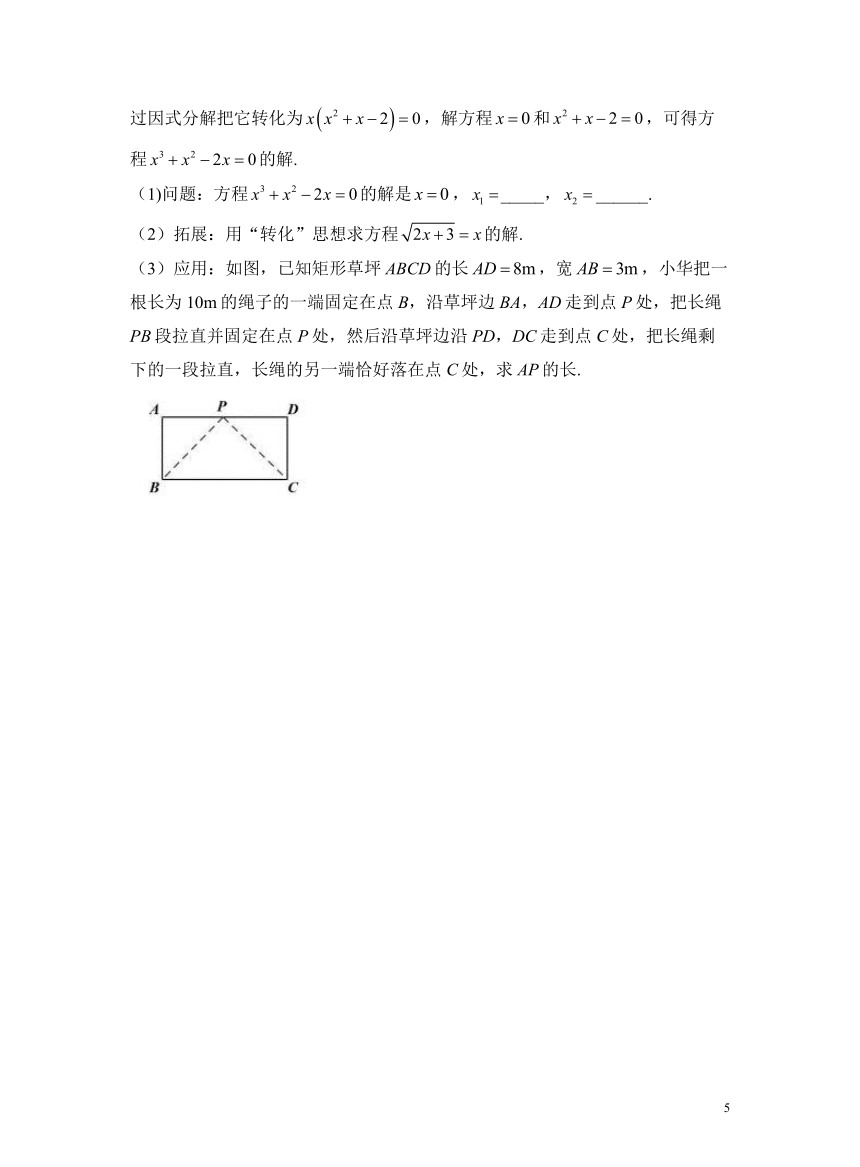
21.(12分)求解一元一次方程,根据等式的基本性质,把方程转化为的形式.求解二元一次方程组,把它转化为一元一次方程来解.类似地,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想—一转化思想,把未知转化为已知.用转化的数学思想,我们还可以解一些新的方程.例如,一元三次方程,可以通过因式分解把它转化为,解方程和,可得方程的解.
(1)问题:方程的解是,_____,______.
(2)拓展:用“转化”思想求方程的解.
(3)应用:如图,已知矩形草坪ABCD的长,宽,小华把一根长为10m的绳子的一端固定在点B,沿草坪边BA,AD走到点P处,把长绳PB段拉直并固定在点P处,然后沿草坪边沿PD,DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C处,求AP的长.
答案以及解析
1.答案:B
解析:一元二次方程程的常数项为0,
,
,
解得,
故选:B.
2.答案:A
解析:,
,
,
,
故选:A.
3.答案:B
解析:,
,
,
,,
,.
故选:B.
4.答案:D
解析:,,方程必有一根为2.
5.答案:D
解析:设运动的时间为ts,
由题意得:,,
,
解得:,,
即当或时,的面积等于.故选D.
6.答案:B
解析:与是“同族二次方程”,
,
,
,
,
最小值为0,
最小值为2017,
即最小值为2017.
故选B.
7.答案:C
解析:是关于x的方程的实数根,
,
整理得,
,
,
,即;
①,
此方程有两个不相等的实数根,故①说法正确;
②,
当时,一定有,故②说法错误;
③是关于x的方程的实数根.且,
b也是关于x的方程的实数根.故③说法正确;
④此方程有两个不相等的实数根,故④说法错误;
所以,正确的结论是①③,
故选:C.
8.答案:B
解析:把关于x的一元二次方程看作为关于的一元二次方程,关于x的一元二次方程的两根分别为,1,或,解得,,即关于x的一元二次方程的两根分别为,.
9.答案:C
解析:设乙驾车的时长为x小时,则甲驾车的时长为小时,
由题知甲的速度为,乙的速度为,
可得方程
解得,(不合题意,舍去),
经检验,是原方程的解,
故选:C.
10.答案:A
解析:关于x的一元二次方程有两个实数根,,,即,且,.,,即,,即,解得或.故选A.
11.答案:9
解析:由题意得,
解得,(舍去),
n的值为9.
12.答案:3
解析:设,
原方程化为:,
解得,,
,
.
故答案为:3.
13.答案:10
解析:设这个最小数为x,则最大数为,根据题意得,整理得,解得,(不合题意,舍去),所以这个最小数为10.
14.答案:-2
解析:根据题意得,整理得,,或,所以,.当时,,舍去,所以x的值为-2.
15.答案:4
解析:设乙的边长为2a,
正方形ABCD和正方形EFGH分别由两张相同的长方形纸片无缝拼接而成,
,,
,,
,,
正方形EFGH的边长为,正方形ABCD的边长为,
,
解得(负值舍去),
,
故答案为:4.
16.答案:(1)
(2)
解析:(1)根据题意得,解得;
(2)k的最大整数为2,
方程可化为,
解此方程得,.
一元二次方程与方程有一个相同的根,
当时,,解得;
当时,,解得,
,即,
m的值为.
17.答案:(1)A种花苗的单价为20元,B种花苗的单价为30元
(2)购买了A种花苗10盆,B种花苗2盆或购买了A种花苗4盆,B种花苗8盆.
解析:(1)设A种花苗的单价为x元,B种花苗的单价为y元,依题意得,
解得
答:A种花苗的单价为20元,B种花苗的单价为30元.
(2)设购买B种花苗m盆,则购买A种花苗盆.依题意得.
整理得,
解得,,
当时,;
当时,,
答:购买了A种花苗10盆,B种花苗2盆或购买了A种花苗4盆,B种花苗8盆.
18.答案:(1),
(2)方程无实数根
(3),
解析:(1)移项,得,
因式分解,得,
解得,.
(2)移项,得.
因为,,,
所以,
所以方程无实数根.
(3)把看成一个整体,
因式分解,得,
整理,得,
解得,.
19.答案:(1)
(2)2
解析:(1)关于x的一元二次方程有实数根,
,
解得:,
即m的取值范围是;
(2),,
,
,
,即,
解得或.
;
.
故m的值为2.
20.答案:(1)800;;(2)每个台灯的售价为37元;(3)月获利不能达到9600元,理由见解析.
解析:(1)售价每下降1元,其月销售量就增加200个,
若售价下降1元,每月能售出个台灯,若售价下降x元(),每月能售出个台灯;
(2)设每个台灯的售价为x元,
由题意得:,
解得:,,
当时,(舍去),
当时,(符合题意),
答:每个台灯的售价为37元;
(3)月获利不能达到9600元,
理由:设每个台灯的售价为x元,
由题意得:,
整理得:,
,
方程无实数根,即月获利不能达到9600元.
21.答案:(1)-2;1
(2)
(3)4m
解析:(1)略
(2)方程的两边平方,得,
整理,得,
因式分解,得,
或,
,,
当时,,
不是原方程的解,
方程的解是;
(3)四边形ABCD是矩形,
,,
设,则,
,,,
,
,
两边平方,得,
整理,得,
两边平方并整理,得,即,
解得.
经检验,是方程的解。
答:AP的长为4m.
1
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.若关于x的一元二次方程的常数项为0,则a的值等于( )
A.1 B.2 C.1或2 D.0
2.用配方法解方程的过程中,应将此方程化为( )
A. B. C. D.
3.方程的根为( )
A., B., C. D.
4.若,则一元二次方程必有一根是( )
A.0 B.无法确定 C.-2 D.2
5.如图,在中,,cm,cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从顶点C出发,沿线段CB向点B方向运动,如果点P的速度是2cm/s,点Q的速度是1cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动,当P,Q两点运动( )秒时,的面积等于.
A.1 B.3 C.3或5 D.1或5
6.新定义,若关于x的一元二次方程:与,称为“同族二次方程”.如与是“同族二次方程”.现有关于x的一元二次方程:与是“同族二次方程”.那么代数式能取的最小值是( )
A.2015 B.2017 C.2022 D.2027
7.已知是关于x的方程的实数根.下列说法:
①此方程有两个不相等的实数根;
②当时,一定有;
③b是此方程的根;
④此方程有两个相等的实数根.上述说法中,正确的有( )
A.①② B.②③ C.①③ D.③④
8.若关于x的一元二次方程的两根分别为,1,则关于x的一元二次方程的两根分别为( )
A., B.,
C., D.,
9.甲、乙两人同驾一辆车出游,各匀速驾驶一半路程,共用3小时,到达目的地后,甲对乙说:“我用你所花的时间,可以行驶”乙对甲说:“我用你所花的时间,只能行驶”.从他们的交谈中可以判断,乙驾车的时长为( )
A.1.2小时 B.1.6小时 C.1.8小时 D.2小时
10.若关于x的一元二次方程有两个实数根,,且,则( )
A.2或6 B.2或8 C.2 D.6
二、填空题(每小题4分,共20分)
11.网上流行一个游戏,发起游戏的人首先发出一个“祝福”链接,将这个“祝福”链接发给n个人,收到链接的人也需把链接发给相同数量的新人,经过两轮传播后,共有91人参与了这个“祝福”链接的传播,则n的值为________.
12.已知,则的值等于________.
13.在2022年7月的日历表上用一个方框圈出4个数(如图所示),若圈出的4个数中,最小数与最大数的乘积为180,则这个最小数为__________.
14.如图,数轴上点A代表的数为,点B代表的数为,已知,且点A在数轴的负半轴上,则x的值为__________.
15.如图,正方形ABCD和正方形EFGH分别由两张相同的长方形纸片无缝拼接而成,现将其摆放在桌面上,如图所示,重合部分为甲、乙、丙,其中乙为正方形,记甲、丙的面积分别为,,若,且桌面被所有纸片覆盖区域的面积为,则乙的面积为_______________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)关于x的一元二次方程有实数根.
(1)求k的取值范围:
(2)如果k是符合条件的最大整数,且一元二次方程与方程有一个相同的根,求此时m的值.
17.(8分)新学期开始时.某校九年级一班的同学为了增添教室绿色文化,准备到一家植物种植基地购买A,B两种花苗,据了解,购买A种花苗3盆,B种花苗5盆,需210元;购买A种花苗4盆,B种花苗10盆,需380元.
(1)求A,B两种花苗的单价分别是多少元;
(2)经九年级一班班委会商定,决定购买A,B两种花苗共12盆进行搭配装扮教室.种植基地销售人员为了支持本次活动,为该班同学提供以下优惠:购买多少盆B种花苗,B种花苗每盆就降价多少元.若九年级一班的同学本次购买花苗共花费了256元,请计算出本次购买了A,B两种花苗各多少盆.
18.(10分)用适当的方法解下列方程:
(1);
(2);
(3).
19.(10分)已知关于x的一元二次方程.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为,,且满足,求实数m的值.
20.(12分)某淘宝网店销售台灯,成本为每个30元.销售大数据分析表明:当每个台灯售价为40元时,平均每月售出600个;若售价每下降1元,其月销售量就增加200个.
(1)若售价下降1元,每月能售出_______个台灯,若售价下降x元(),每月能售出____个台灯.
(2)为迎接“双十一”,该网店决定降价促销,在库存为1210个台灯的情况下,若预计月获利恰好为8400元,求每个台灯的售价.
(3)月获利能否达到9600元,说明理由.
21.(12分)求解一元一次方程,根据等式的基本性质,把方程转化为的形式.求解二元一次方程组,把它转化为一元一次方程来解.类似地,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想—一转化思想,把未知转化为已知.用转化的数学思想,我们还可以解一些新的方程.例如,一元三次方程,可以通过因式分解把它转化为,解方程和,可得方程的解.
(1)问题:方程的解是,_____,______.
(2)拓展:用“转化”思想求方程的解.
(3)应用:如图,已知矩形草坪ABCD的长,宽,小华把一根长为10m的绳子的一端固定在点B,沿草坪边BA,AD走到点P处,把长绳PB段拉直并固定在点P处,然后沿草坪边沿PD,DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C处,求AP的长.
答案以及解析
1.答案:B
解析:一元二次方程程的常数项为0,
,
,
解得,
故选:B.
2.答案:A
解析:,
,
,
,
故选:A.
3.答案:B
解析:,
,
,
,,
,.
故选:B.
4.答案:D
解析:,,方程必有一根为2.
5.答案:D
解析:设运动的时间为ts,
由题意得:,,
,
解得:,,
即当或时,的面积等于.故选D.
6.答案:B
解析:与是“同族二次方程”,
,
,
,
,
最小值为0,
最小值为2017,
即最小值为2017.
故选B.
7.答案:C
解析:是关于x的方程的实数根,
,
整理得,
,
,
,即;
①,
此方程有两个不相等的实数根,故①说法正确;
②,
当时,一定有,故②说法错误;
③是关于x的方程的实数根.且,
b也是关于x的方程的实数根.故③说法正确;
④此方程有两个不相等的实数根,故④说法错误;
所以,正确的结论是①③,
故选:C.
8.答案:B
解析:把关于x的一元二次方程看作为关于的一元二次方程,关于x的一元二次方程的两根分别为,1,或,解得,,即关于x的一元二次方程的两根分别为,.
9.答案:C
解析:设乙驾车的时长为x小时,则甲驾车的时长为小时,
由题知甲的速度为,乙的速度为,
可得方程
解得,(不合题意,舍去),
经检验,是原方程的解,
故选:C.
10.答案:A
解析:关于x的一元二次方程有两个实数根,,,即,且,.,,即,,即,解得或.故选A.
11.答案:9
解析:由题意得,
解得,(舍去),
n的值为9.
12.答案:3
解析:设,
原方程化为:,
解得,,
,
.
故答案为:3.
13.答案:10
解析:设这个最小数为x,则最大数为,根据题意得,整理得,解得,(不合题意,舍去),所以这个最小数为10.
14.答案:-2
解析:根据题意得,整理得,,或,所以,.当时,,舍去,所以x的值为-2.
15.答案:4
解析:设乙的边长为2a,
正方形ABCD和正方形EFGH分别由两张相同的长方形纸片无缝拼接而成,
,,
,,
,,
正方形EFGH的边长为,正方形ABCD的边长为,
,
解得(负值舍去),
,
故答案为:4.
16.答案:(1)
(2)
解析:(1)根据题意得,解得;
(2)k的最大整数为2,
方程可化为,
解此方程得,.
一元二次方程与方程有一个相同的根,
当时,,解得;
当时,,解得,
,即,
m的值为.
17.答案:(1)A种花苗的单价为20元,B种花苗的单价为30元
(2)购买了A种花苗10盆,B种花苗2盆或购买了A种花苗4盆,B种花苗8盆.
解析:(1)设A种花苗的单价为x元,B种花苗的单价为y元,依题意得,
解得
答:A种花苗的单价为20元,B种花苗的单价为30元.
(2)设购买B种花苗m盆,则购买A种花苗盆.依题意得.
整理得,
解得,,
当时,;
当时,,
答:购买了A种花苗10盆,B种花苗2盆或购买了A种花苗4盆,B种花苗8盆.
18.答案:(1),
(2)方程无实数根
(3),
解析:(1)移项,得,
因式分解,得,
解得,.
(2)移项,得.
因为,,,
所以,
所以方程无实数根.
(3)把看成一个整体,
因式分解,得,
整理,得,
解得,.
19.答案:(1)
(2)2
解析:(1)关于x的一元二次方程有实数根,
,
解得:,
即m的取值范围是;
(2),,
,
,
,即,
解得或.
;
.
故m的值为2.
20.答案:(1)800;;(2)每个台灯的售价为37元;(3)月获利不能达到9600元,理由见解析.
解析:(1)售价每下降1元,其月销售量就增加200个,
若售价下降1元,每月能售出个台灯,若售价下降x元(),每月能售出个台灯;
(2)设每个台灯的售价为x元,
由题意得:,
解得:,,
当时,(舍去),
当时,(符合题意),
答:每个台灯的售价为37元;
(3)月获利不能达到9600元,
理由:设每个台灯的售价为x元,
由题意得:,
整理得:,
,
方程无实数根,即月获利不能达到9600元.
21.答案:(1)-2;1
(2)
(3)4m
解析:(1)略
(2)方程的两边平方,得,
整理,得,
因式分解,得,
或,
,,
当时,,
不是原方程的解,
方程的解是;
(3)四边形ABCD是矩形,
,,
设,则,
,,,
,
,
两边平方,得,
整理,得,
两边平方并整理,得,即,
解得.
经检验,是方程的解。
答:AP的长为4m.
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
