初中数学人教版九年级下册第二十七章 27.2.2相似三角形的性质
文档属性
| 名称 | 初中数学人教版九年级下册第二十七章 27.2.2相似三角形的性质 |

|
|
| 格式 | docx | ||
| 文件大小 | 632.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-25 15:53:21 | ||
图片预览


文档简介
九年级下册26章《反比例函数》导学案 【编号:01】 26.1.1反比例函数
多少事,从来急;天地转,光阴迫,一万年太久,只争朝夕
九年级下册27章《相似》导学案 【编号:09】 27.2相似三角形
27.2.2 相似三角形的性质
目标导学
1.背诵并会概述相似三角形的性质;(重点)
2.会利用相似三角形的性质解决简单的问题.(难点)
二、新知导入
两个三角形相似,除了对应边成比例、对应角相等之外,还可以得到许多有用的结论.例如,在图中,△ABC和△A′B′C′是两个相似三角形,相似比为k,其中AD、A′D′分别为BC、B′C′边上的高,那么AD、A′D′之间有什么关系?
三、新知探究
知识点一:相似三角形的性质(对应线段的比、周长的比)
根据三角形相似的定义可知,相似三角形的对应角相等,对应边成比例。
下面我们研究下相似三角形的其他几何量之间的关系。
探究:
如图,∽,相似比是,它们对应高,对应中线、对应角平分线的比各是多少?
解:如图,分别作和的对应高和.
∵ ∽,
∴
又∵和都是直角三角形,
∴_________________。
所以( )=
由此我们可以得到:
相似三角形对应高的比等于________。
类似的,我们可以得到:
相似三角形对应中线的比、对应角平分线的比都等于__________。
一般的,我们有:
相似三角形对应线段的比等于相似比。
【典例一】已知 △ABC∽△DEF,BG、EH 分别是 △ABC和 △DEF 的角平分线,BC = 6 cm,EF = 4cm,BG= 4.8 cm. 求 EH 的长.
(跟踪训练)1、如果两个相似三角形的对应高的比为 2 : 3,那么对应角平分线的比是 ,对应边上的中线的比是_________ 。
(跟踪训练)2、△ABC 与 △A'B'C' 的相似比为3 : 4,若 BC 边上的高 AD=12 cm,则 B'C' 边上的高 A'D'= 。
(跟踪训练)3、△ABC的三边长分别为3,4,5,与它相似的△DEF的最小边长为6,则△DEF最长边上的中线长为( )
A、4 B、5 C、6 D、7
思考:相似三角形的周长比是否也等于相似比?如果是,为什么?给出证明过程。
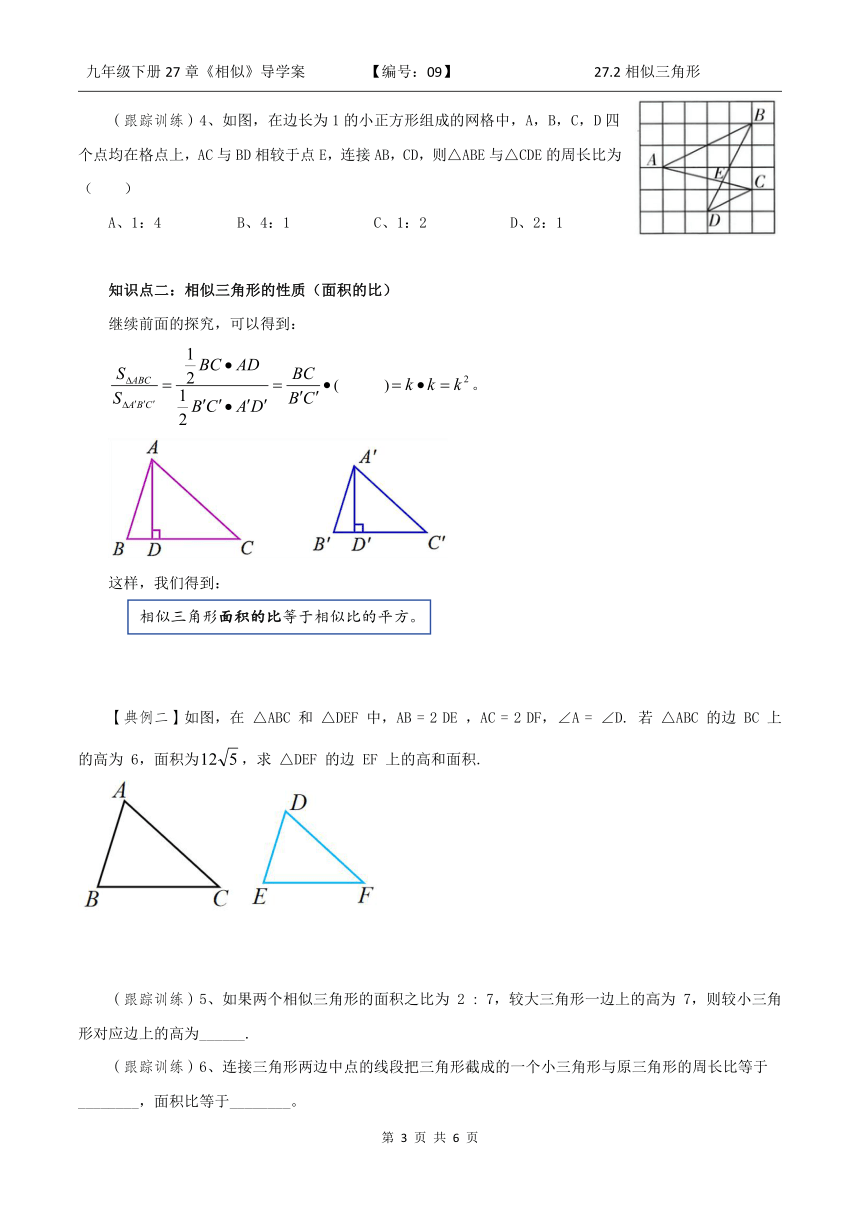
(跟踪训练)4、如图,在边长为1的小正方形组成的网格中,A,B,C,D四个点均在格点上,AC与BD相较于点E,连接AB,CD,则△ABE与△CDE的周长比为( )
A、1:4 B、4:1 C、1:2 D、2:1
知识点二:相似三角形的性质(面积的比)
继续前面的探究,可以得到:
( )。
这样,我们得到:
相似三角形面积的比等于相似比的平方。
【典例二】如图,在 △ABC 和 △DEF 中,AB = 2 DE ,AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为,求 △DEF 的边 EF 上的高和面积.
(跟踪训练)5、如果两个相似三角形的面积之比为 2 : 7,较大三角形一边上的高为 7,则较小三角形对应边上的高为______.
(跟踪训练)6、连接三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于________,面积比等于________。
(跟踪训练)7、如图,D,E分别是AC,AB上的点,已知△ABC的面积为100,且,求四边形BCDE 的面积.
四、当堂达标
基础
1、两个相似三角形的一对对应边分别是 35 cm、14 cm,
(1) 它们的周长差 60 cm,这两个三角形的周长分别是________________;
(2) 它们的面积之和是 58 cm2,这两个三角形的面积分别是________________;
2、在一张缩印出来的纸上,一个三角形的面积由原图中的9变成了4,则缩印出的三角形的周长是原图中三角形周长的( )
A、 B、 C、 D、
3、如图,在正方形网格中,点A,B,C,D是网格线交点,AC与BD相交与点O,则△ABO的面积与△CDO的面积的比为( )
A、1:2 B、2:3 C、1:4 D、3:4
如图是某晾衣架的侧面示意图,根据图中数据,C,D两点间的距离是( )
A、0.9m B、1.2m C、1.5m D、2.5m
5、如图,小华自制了一个小孔成像装置,蜡烛的长度为15cm,小孔O到蜡烛AB的距离是50cm,纸筒的长度为10cm,则像CD的长为( )
A、3cm B、5cm C、8cm D、10cm
第3题图 第4题图 第5题图
综合
6、已知△与△相似,AD,BE是△ABC的高,,是△的高,若AD=4,BE=3,,的长为____________。
7、如图,△∽△,CG,FH分别为边AB,DE上的高。
∠ACG________∠DFH;(填“≠”或“=”)
若,,则AC的长为______________;
若△ABC与△DEF对应边的比是5:3,则△ABC与△DEF的面积之比是____________,△BCG与△EFH的面积之比为_____________。
若AG:DH=4:3,则△ABC与△DEF的周长之比为___________。
若CG=3,FH=2,且△ABC与△DEF的周长相差10,则△ABC的周长为__________。
第7题图 第8题图 第9题图
8、如图,已知△ABC的面积为 12,BC=6。将△ABC沿直线 BC 向右平移 2个单位长度,得到△DEF,AC与DE 交于点 M,作MN⊥BC于N,则MN=_________。
9、如图,E是平行四边形ABCD的边AD上的一点,CE与BA的延长线交于F,若,则______________。
中考
(遵义中考)如图,△ABO的顶点A在函数的图像上,∠ABO=90°,过AO边的三等分点M,N分别作x轴的平行线交AB于点P,Q。若四边形MNQP的面积为3,则k的值为( )
A、9 B、12 C、15 D、18
如图,四边形ABCD是平行四边形,DE交AC于点F,.
求证:△AEF∽△CDF;
若△CDF的面积为32,求△ADF的面积
如图,在Rt△ABC中,∠ABC=90°,以△ABC的一条直角边AB为斜边,向外作Rt△ABD,延长AD交CB的延长线于点E,已知AB·BD=AD·BC。
求证:△ABC∽△ADB;
若AC=10,BE=6,求的值。
五、课后总结
多少事,从来急;天地转,光阴迫,一万年太久,只争朝夕
九年级下册27章《相似》导学案 【编号:09】 27.2相似三角形
27.2.2 相似三角形的性质
目标导学
1.背诵并会概述相似三角形的性质;(重点)
2.会利用相似三角形的性质解决简单的问题.(难点)
二、新知导入
两个三角形相似,除了对应边成比例、对应角相等之外,还可以得到许多有用的结论.例如,在图中,△ABC和△A′B′C′是两个相似三角形,相似比为k,其中AD、A′D′分别为BC、B′C′边上的高,那么AD、A′D′之间有什么关系?
三、新知探究
知识点一:相似三角形的性质(对应线段的比、周长的比)
根据三角形相似的定义可知,相似三角形的对应角相等,对应边成比例。
下面我们研究下相似三角形的其他几何量之间的关系。
探究:
如图,∽,相似比是,它们对应高,对应中线、对应角平分线的比各是多少?
解:如图,分别作和的对应高和.
∵ ∽,
∴
又∵和都是直角三角形,
∴_________________。
所以( )=
由此我们可以得到:
相似三角形对应高的比等于________。
类似的,我们可以得到:
相似三角形对应中线的比、对应角平分线的比都等于__________。
一般的,我们有:
相似三角形对应线段的比等于相似比。
【典例一】已知 △ABC∽△DEF,BG、EH 分别是 △ABC和 △DEF 的角平分线,BC = 6 cm,EF = 4cm,BG= 4.8 cm. 求 EH 的长.
(跟踪训练)1、如果两个相似三角形的对应高的比为 2 : 3,那么对应角平分线的比是 ,对应边上的中线的比是_________ 。
(跟踪训练)2、△ABC 与 △A'B'C' 的相似比为3 : 4,若 BC 边上的高 AD=12 cm,则 B'C' 边上的高 A'D'= 。
(跟踪训练)3、△ABC的三边长分别为3,4,5,与它相似的△DEF的最小边长为6,则△DEF最长边上的中线长为( )
A、4 B、5 C、6 D、7
思考:相似三角形的周长比是否也等于相似比?如果是,为什么?给出证明过程。
(跟踪训练)4、如图,在边长为1的小正方形组成的网格中,A,B,C,D四个点均在格点上,AC与BD相较于点E,连接AB,CD,则△ABE与△CDE的周长比为( )
A、1:4 B、4:1 C、1:2 D、2:1
知识点二:相似三角形的性质(面积的比)
继续前面的探究,可以得到:
( )。
这样,我们得到:
相似三角形面积的比等于相似比的平方。
【典例二】如图,在 △ABC 和 △DEF 中,AB = 2 DE ,AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为,求 △DEF 的边 EF 上的高和面积.
(跟踪训练)5、如果两个相似三角形的面积之比为 2 : 7,较大三角形一边上的高为 7,则较小三角形对应边上的高为______.
(跟踪训练)6、连接三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于________,面积比等于________。
(跟踪训练)7、如图,D,E分别是AC,AB上的点,已知△ABC的面积为100,且,求四边形BCDE 的面积.
四、当堂达标
基础
1、两个相似三角形的一对对应边分别是 35 cm、14 cm,
(1) 它们的周长差 60 cm,这两个三角形的周长分别是________________;
(2) 它们的面积之和是 58 cm2,这两个三角形的面积分别是________________;
2、在一张缩印出来的纸上,一个三角形的面积由原图中的9变成了4,则缩印出的三角形的周长是原图中三角形周长的( )
A、 B、 C、 D、
3、如图,在正方形网格中,点A,B,C,D是网格线交点,AC与BD相交与点O,则△ABO的面积与△CDO的面积的比为( )
A、1:2 B、2:3 C、1:4 D、3:4
如图是某晾衣架的侧面示意图,根据图中数据,C,D两点间的距离是( )
A、0.9m B、1.2m C、1.5m D、2.5m
5、如图,小华自制了一个小孔成像装置,蜡烛的长度为15cm,小孔O到蜡烛AB的距离是50cm,纸筒的长度为10cm,则像CD的长为( )
A、3cm B、5cm C、8cm D、10cm
第3题图 第4题图 第5题图
综合
6、已知△与△相似,AD,BE是△ABC的高,,是△的高,若AD=4,BE=3,,的长为____________。
7、如图,△∽△,CG,FH分别为边AB,DE上的高。
∠ACG________∠DFH;(填“≠”或“=”)
若,,则AC的长为______________;
若△ABC与△DEF对应边的比是5:3,则△ABC与△DEF的面积之比是____________,△BCG与△EFH的面积之比为_____________。
若AG:DH=4:3,则△ABC与△DEF的周长之比为___________。
若CG=3,FH=2,且△ABC与△DEF的周长相差10,则△ABC的周长为__________。
第7题图 第8题图 第9题图
8、如图,已知△ABC的面积为 12,BC=6。将△ABC沿直线 BC 向右平移 2个单位长度,得到△DEF,AC与DE 交于点 M,作MN⊥BC于N,则MN=_________。
9、如图,E是平行四边形ABCD的边AD上的一点,CE与BA的延长线交于F,若,则______________。
中考
(遵义中考)如图,△ABO的顶点A在函数的图像上,∠ABO=90°,过AO边的三等分点M,N分别作x轴的平行线交AB于点P,Q。若四边形MNQP的面积为3,则k的值为( )
A、9 B、12 C、15 D、18
如图,四边形ABCD是平行四边形,DE交AC于点F,.
求证:△AEF∽△CDF;
若△CDF的面积为32,求△ADF的面积
如图,在Rt△ABC中,∠ABC=90°,以△ABC的一条直角边AB为斜边,向外作Rt△ABD,延长AD交CB的延长线于点E,已知AB·BD=AD·BC。
求证:△ABC∽△ADB;
若AC=10,BE=6,求的值。
五、课后总结
