三角形全等的条件
图片预览


文档简介
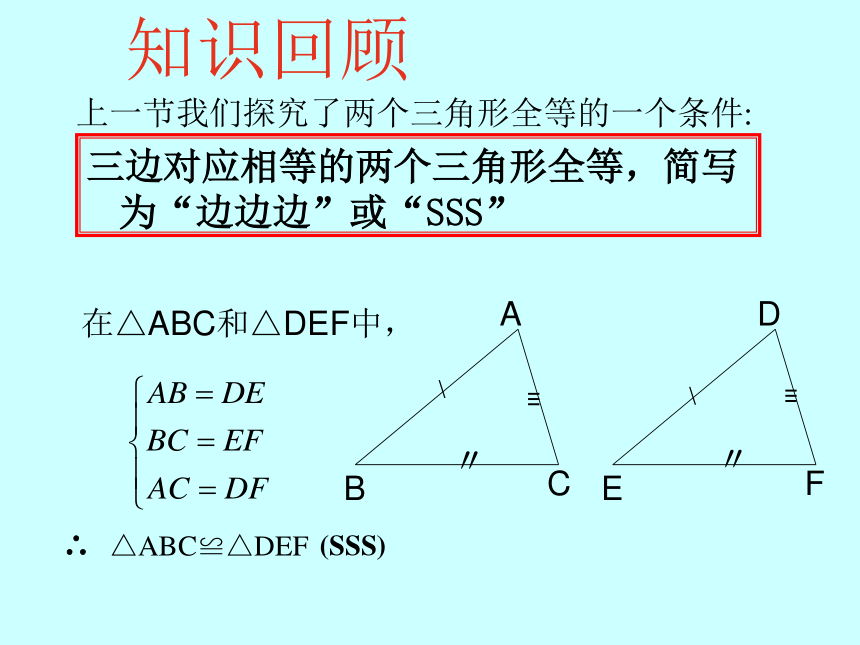
课件19张PPT。13.2探索三角形全等的条件(SAS)三边对应相等的两个三角形全等,简写为“边边边”或“SSS”在△ABC和△DEF中,△ABC≌△DEF∴(SSS) 上一节我们探究了两个三角形全等的一个条件:知识回顾除了SSS外,还有其他情况吗?今天我们继续探索三角形全等的条件.思考(2) 三条边(1) 三个角(3) 两边一角(4) 两角一边 当两个三角形满足六个条件中的三个时,有四种情况:SSS不能!?活动1:
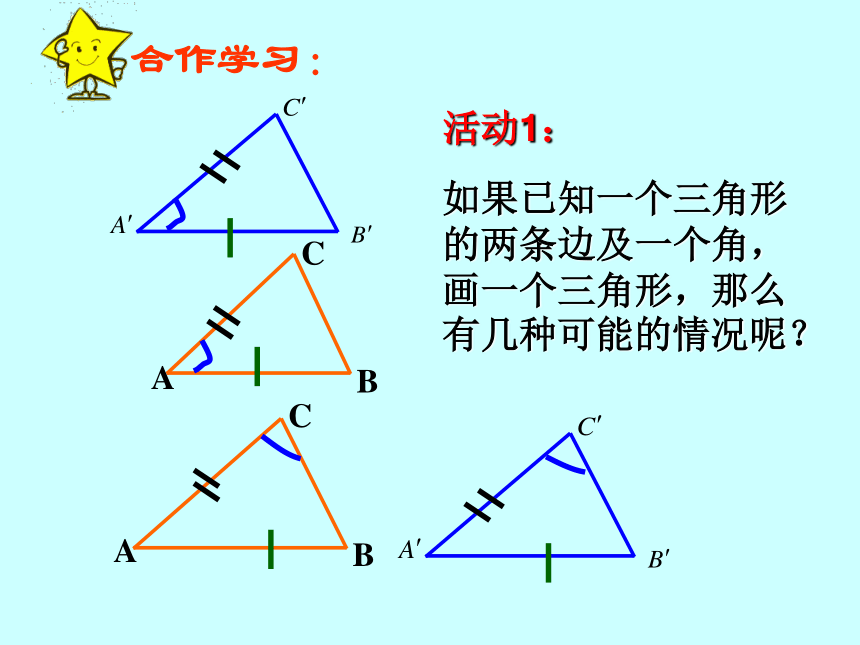
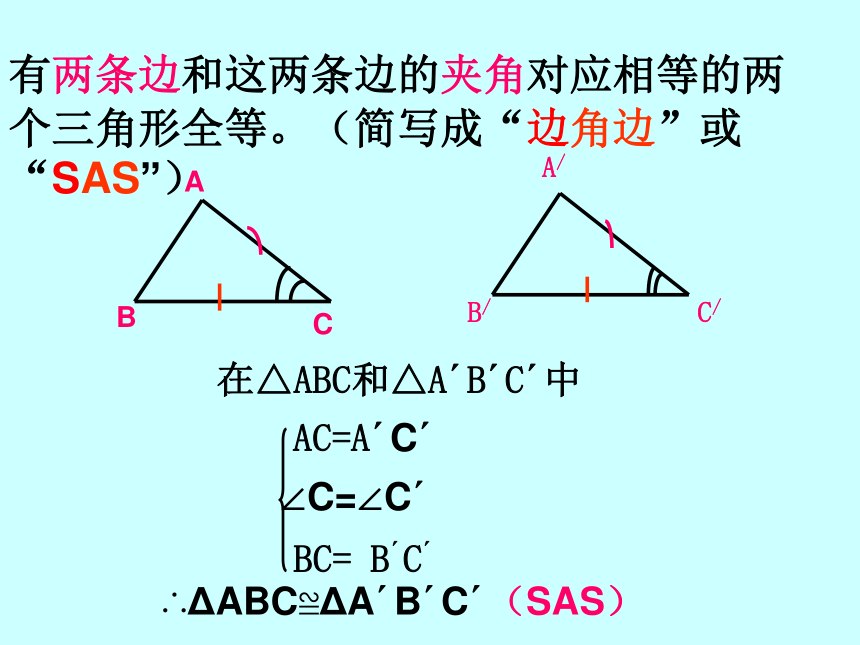
如果已知一个三角形的两条边及一个角,画一个三角形,那么有几种可能的情况呢?在△ABC和△A′B′C′中
AC=A′C′
∠C=∠C′
BC= B′C′
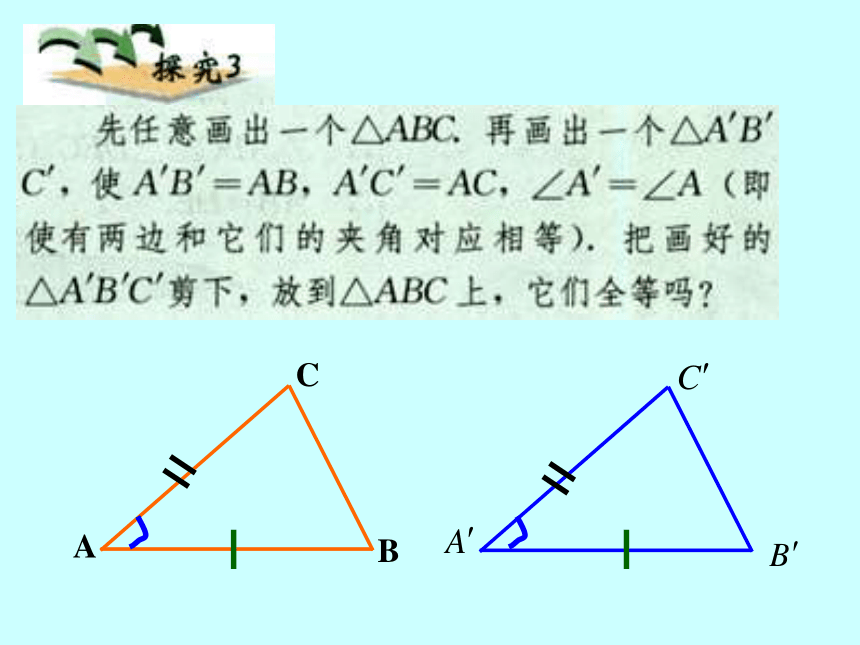
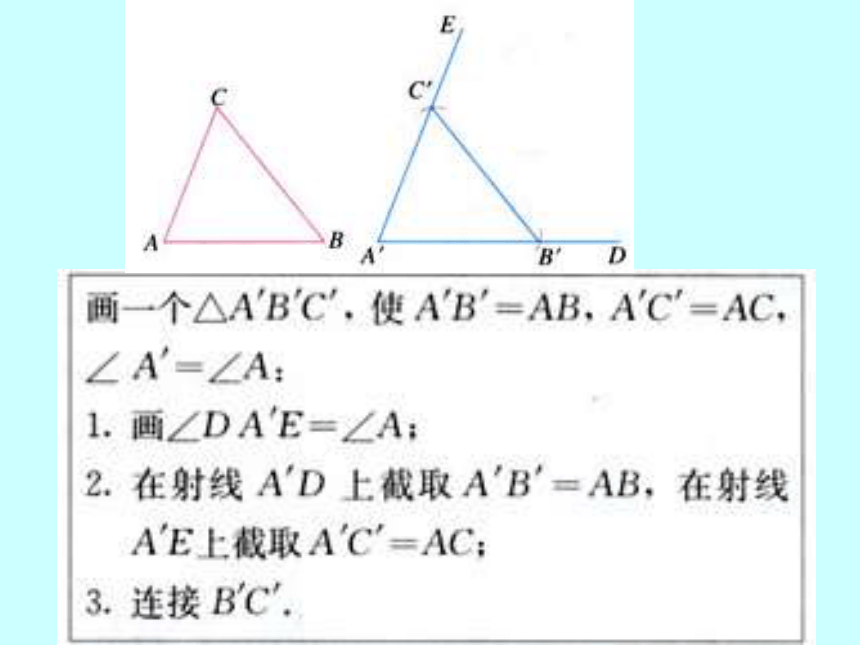
∴ΔABC≌ΔA′B′C′(SAS)有两条边和这两条边的夹角对应相等的两
个三角形全等。(简写成“边角边”或“SAS”)已知:如图, AB=CB ,∠ ABD= ∠ CBD
△ ABD 和△ CBD 全等吗?
ABCD现在例1的已知条件不改变,而问题改变成:
问AD=CD,
BD平分∠ADC吗?
ABCD练习 (2) 已知:AD=CD, BD 平分∠ ADC 。
问∠A=∠ C 吗?大显身手
例1 如图AC与BD相交于点O,已知OA=OC,OB=OD,说明△AOB≌△COD的理由。例2 如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?说明理由。归纳:判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到。l.利用全等三角形证明线段或角相等, 是证明线段 或角相等的重要方法之一,其思路如下:
⑴观察要证的线段和角在哪两个可能全等的三角形之中.
⑵分析要证全等的这两个三角形,已知什么条件,还缺什么条件.
⑶设法证出所缺的条件.归纳:创设情景 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。怎样测出A、B两杆之间的距离呢?。AB 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。想一想 AC=DC?
∠ACB=∠DCE
BC=EC △ACB≌△DCE
AB=DE小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。△EDH≌△FDH 根据“SAS”,所以EH=FH你来试试 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?ABCDEF2.5cm3.5cm40°40°3.5cm2.5cm结论:两边及其一边所对的角相等,两个三角形不一定全等探究2探索思考:如果两个三角形有两边和一个
角对应相等,这样的两个三角形全等吗?ABC“两边一角”对应相等的两个三角形不一定全等两边及其中一边的对角 通过本堂课的学习和探索,你学会了什么?
2. 谈一谈!你对这堂课的感受?
在实际生活中, 我们面对不能直接测量物
体的宽度或距离时. 可以把它们转化为数学问
题,通过三角形全等,再利用对应边相等来解决!
忆一忆,谈一谈AB=DE,求证:AC=DF, ∠A= ∠D
AC∥DF结束寄语数学源于生活,又反过来服务于生活.如果你无愧于数学,那数学就可以助你到达胜利的彼岸.
如果已知一个三角形的两条边及一个角,画一个三角形,那么有几种可能的情况呢?在△ABC和△A′B′C′中
AC=A′C′
∠C=∠C′
BC= B′C′
∴ΔABC≌ΔA′B′C′(SAS)有两条边和这两条边的夹角对应相等的两
个三角形全等。(简写成“边角边”或“SAS”)已知:如图, AB=CB ,∠ ABD= ∠ CBD
△ ABD 和△ CBD 全等吗?
ABCD现在例1的已知条件不改变,而问题改变成:
问AD=CD,
BD平分∠ADC吗?
ABCD练习 (2) 已知:AD=CD, BD 平分∠ ADC 。
问∠A=∠ C 吗?大显身手
例1 如图AC与BD相交于点O,已知OA=OC,OB=OD,说明△AOB≌△COD的理由。例2 如图,AC=BD,∠CAB= ∠DBA,你能判断BC=AD吗?说明理由。归纳:判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到。l.利用全等三角形证明线段或角相等, 是证明线段 或角相等的重要方法之一,其思路如下:
⑴观察要证的线段和角在哪两个可能全等的三角形之中.
⑵分析要证全等的这两个三角形,已知什么条件,还缺什么条件.
⑶设法证出所缺的条件.归纳:创设情景 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。怎样测出A、B两杆之间的距离呢?。AB 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。想一想 AC=DC?
∠ACB=∠DCE
BC=EC △ACB≌△DCE
AB=DE小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。△EDH≌△FDH 根据“SAS”,所以EH=FH你来试试 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?ABCDEF2.5cm3.5cm40°40°3.5cm2.5cm结论:两边及其一边所对的角相等,两个三角形不一定全等探究2探索思考:如果两个三角形有两边和一个
角对应相等,这样的两个三角形全等吗?ABC“两边一角”对应相等的两个三角形不一定全等两边及其中一边的对角 通过本堂课的学习和探索,你学会了什么?
2. 谈一谈!你对这堂课的感受?
在实际生活中, 我们面对不能直接测量物
体的宽度或距离时. 可以把它们转化为数学问
题,通过三角形全等,再利用对应边相等来解决!
忆一忆,谈一谈AB=DE,求证:AC=DF, ∠A= ∠D
AC∥DF结束寄语数学源于生活,又反过来服务于生活.如果你无愧于数学,那数学就可以助你到达胜利的彼岸.
