第五章 相交线与平行线 单元练习(含答案) 2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 第五章 相交线与平行线 单元练习(含答案) 2023-2024学年初中数学人教版七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 316.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-25 22:38:12 | ||
图片预览



文档简介
第五章 相交线与平行线
(时间:120分钟 分值:120分)
一、单项选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
1.如图,在平面内作已知直线m的垂线,可作的垂线有 ( )
A.0条 B.1条
C.2条 D.无数条
2.下面四个图形中,∠1与∠2是同位角的是 ( )
3.如图,已知直线a,b被直线c所截,下列条件不能判断a∥b的是 ( )
A.∠2=∠6
B.∠3+∠4=180°
C.∠2+∠5=180°
D.∠1=∠6
4.下列命题中,为假命题的是 ( )
A.内错角相等,两直线平行
B.同角的补角相等
C.两直线平行,同位角互补
D.过直线外一点有且只有一条直线与已知直线平行
5.如图,∠1=∠2,∠4=120°,则∠3等于 ( )
A.60°
B.40°
C.50°
D.30°
6.2022年北京冬奥会男子500米短道速滑冠军在一次直道速滑训练中,经过两次拐弯后的速滑方向与原来的方向相反,则两次拐弯的角度可能是 ( )
A.第一次向左拐52°,第二次向右拐52°
B.第一次向左拐48°,第二次向左拐48°
C.第一次向左拐73°,第二次向右拐107°
D.第一次向左拐32°,第二次向左拐148°
二、填空题(本大题共6小题,每小题3分,共18分)
7.如图,某单位要在河岸l上建一个水泵房引水到C处.他们的做法如下:过点C作CD⊥l于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是 .
8.已知直线a∥b,把一块含30°角的直角三角板按如图所示的方式放置,若∠1=48°,则∠2的度数为 .
9.如图,已知m∥n,若∠1+∠2=280°,则∠4-∠3= .
10.如图,在宽为13米、长为24米的长方形地面上修筑同样宽的道路(图中阴影部分),道路的宽为2米,余下部分种植草坪.则草坪的面积为 平方米.
11.如图,将长方形纸片ABCD沿折痕MN折叠,A,B分别落在对应位置A1,B1处,A1B1交AD于点E,若∠BNM=62°,则∠A1ME的度数为 .
12.如图,直线AB和CD交于点O,∠AOC=30°,∠BOE=90°,OF平分∠AOD.射线OE以每秒10°的速度绕点O逆时针转动,同时射线OF也以每秒4°的速度绕点O顺时针转动,当射线OE转动一周时,射线OE,OF同时停止转动.在射线OE转动一周的过程中,当OE⊥OF时,射线OE转动的时间为 秒.
三、解答题(本大题共5小题,每小题6分,共30分)
13.(1)如图,点A,O,B在同一条直线上,已知∠BOC=50°,求∠AOC的度数.
(2)如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,求∠BOD的度数.
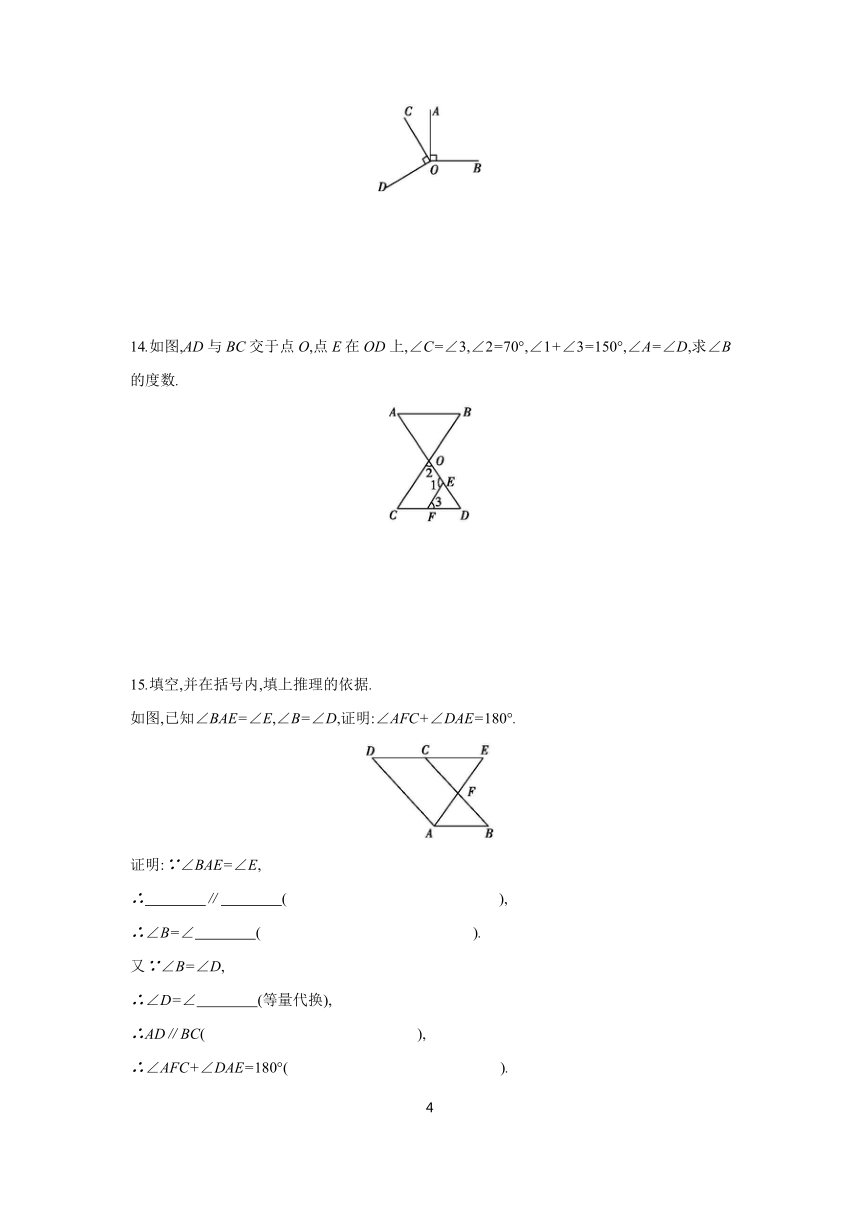
14.如图,AD与BC交于点O,点E在OD上,∠C=∠3,∠2=70°,∠1+∠3=150°,∠A=∠D,求∠B的度数.
15.填空,并在括号内,填上推理的依据.
如图,已知∠BAE=∠E,∠B=∠D,证明:∠AFC+∠DAE=180°.
证明:∵∠BAE=∠E,
∴ ∥ ( ),
∴∠B=∠ ( ).
又∵∠B=∠D,
∴∠D=∠ (等量代换),
∴AD∥BC( ),
∴∠AFC+∠DAE=180°( ).
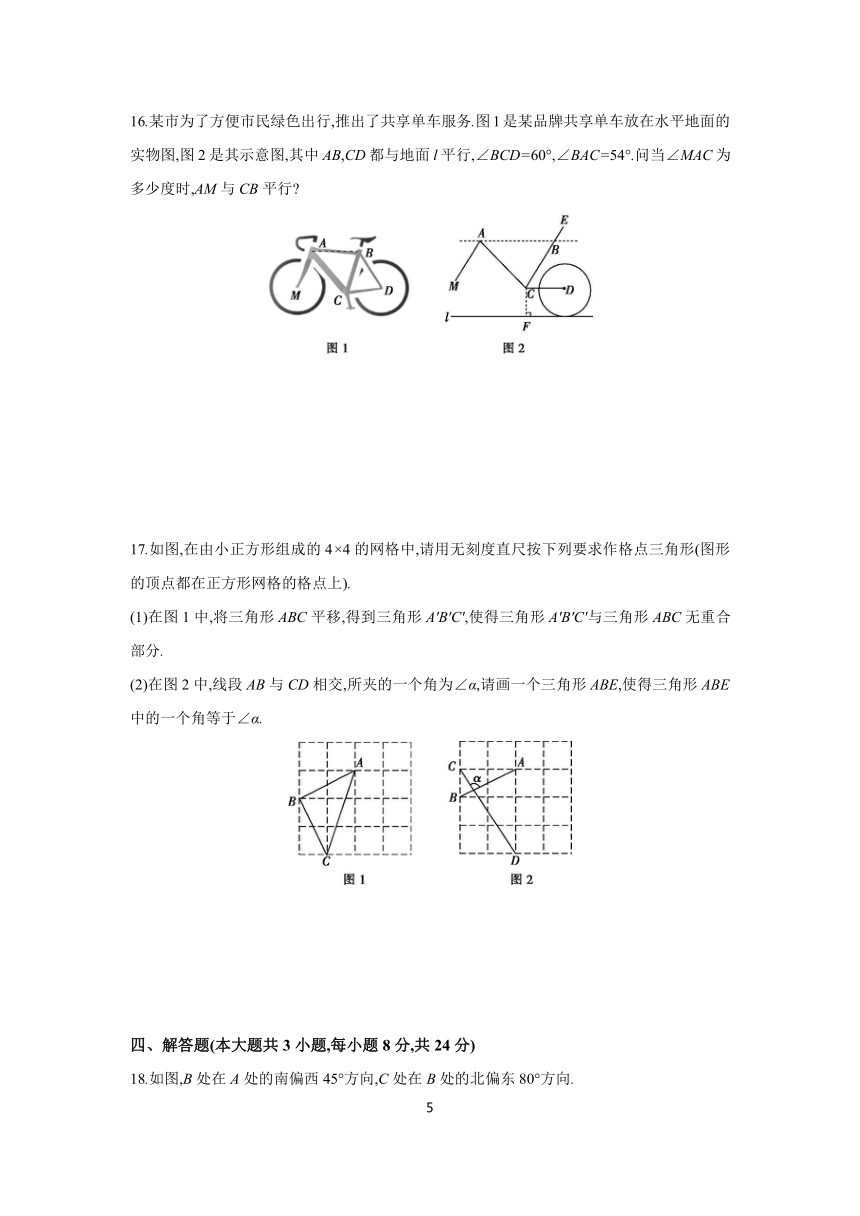
16.某市为了方便市民绿色出行,推出了共享单车服务.图1是某品牌共享单车放在水平地面的实物图,图2是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=54°.问当∠MAC为多少度时,AM与CB平行
17.如图,在由小正方形组成的4×4的网格中,请用无刻度直尺按下列要求作格点三角形(图形的顶点都在正方形网格的格点上).
(1)在图1中,将三角形ABC平移,得到三角形A'B'C',使得三角形A'B'C'与三角形ABC无重合部分.
(2)在图2中,线段AB与CD相交,所夹的一个角为∠α,请画一个三角形ABE,使得三角形ABE中的一个角等于∠α.
四、解答题(本大题共3小题,每小题8分,共24分)
18.如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向.
(1)∠ABC的度数为 .
(2)要使CD∥AB,则∠BCD等于多少度
19.如图,直线AB,CD相交于点O,OB平分∠EOD.
(1)若∠EOC=98°,求∠BOD的度数.
(2)若∠BOE∶∠EOC=1∶3,求∠AOC的度数.
20.如图,点O在直线AB上,OC⊥OD,∠D与∠1互余.
(1)求证:ED∥AB.
(2)OF平分∠AOD交DE于点F,若∠OFD=65°,补全图形,并求∠1的度数.
五、解答题(本大题共2小题,每小题9分,共18分)
21.如图,在三角形ABC中,BC=4 cm,将三角形ABC以0.2 cm/s的速度沿BC所在直线向右平移,所得的图形对应三角形DEF,设运动时间为t s.
(1)请直接写出AB与DE之间的关系.
(2)若∠ADE=60°,求∠B的度数.
(3)当t为何值时,EC=1 cm
22.操作探究,解决问题:
同学们玩游戏,借助两个三角形模板画平行线.
规则1:摆放一副三角板,画平行线.
小颖的做法:如图1,先画一条直线MN,之后按如图所示的方式摆放三角板,即可得到AB∥CD.她的依据是 .
小静的做法:按如图2所示的方式摆放两块三角板,也可得到AB∥CD.她的依据是 .
规则2:请你利用图3所示的两个三角形模板,将其正确摆放后画出平行线.在图4中画出你所摆放的两个三角形模板的位置.
六、解答题(本大题共12分)
23.【问题发现】(1)如图1,直线AB∥CD,连接BE,CE,可以发现∠B+∠C=∠BEC.
请把下面的证明过程补充完整:
证明:过点E作EF∥AB.
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC( ),
∴∠C=∠CEF( ).
∵EF∥AB,
∴∠B=∠BEF(同理),
∴∠B+∠C= (等量代换),
即∠B+∠C=∠BEC.
【拓展探究】(2)如果点E运动到图2所示的位置,其他条件不变,求证:∠B+∠C=360°-∠BEC.
【解决问题】(3)如图3,AB∥DC,E,F,G是AB与CD之间的点,找出∠1,∠2,∠3,∠4,∠5之间的数量关系,并说明理由.
参考答案
1.D 2.C 3.B 4.C 5.A 6.D
7.垂线段最短 8.102° 9.100° 10.242 11.56°
12.或或
提示:当OE,OF还未转动时,∠AOC=30°,∴∠AOD=150°.
∵OF平分∠AOD,∴∠AOF=∠AOD=75°,∴∠EOF=∠AOE+∠AOF=165°.
∵360÷10=36,165÷4=41.25,
∴射线OE转完一周后,射线OF还未到达原射线OE的位置.
设射线OE转动的时间为t秒.
由题意得,165-(10t+4t)=90或10t-(165-4t)=90或360-10t+165-4t=90,
解得t=或或,
∴当射线OE转动的时间为或或秒时,OE⊥OF.
13.(1)解:∠AOC=180°-50°=130°. 3分
(2)解:∠BOD=360°-90°-90°-27°=153°. 3分
14.解:∵∠C=∠3,∴BC∥EF,∴∠1+∠2=180°.
∵∠2=70°,∴∠1=110°.
∵∠1+∠3=150°,∴∠3=40°. 2分
∵∠C=∠3,∴∠C=40°.
∵∠A=∠D,∴AB∥CD,
∴∠B=∠C=40°. 6分
15.解:AB;DE;内错角相等,两直线平行; 2分
BCE;两直线平行,内错角相等; 3分
BCE; 4分
同位角相等,两直线平行; 5分
两直线平行,同旁内角互补. 6分
16.解:∵AB,CD都与地面l平行,
∴AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠BAC+∠ACB+∠BCD=180°. 3分
∵∠BCD=60°,∠BAC=54°,
∴∠ACB=66°,
∴当∠MAC=∠ACB=66°时,AM∥CB. 6分
17.解:(1)如图1,三角形A'B'C'即为所作. 3分
(2)如图2,三角形ABE即为所作,∠BAE=∠α. 6分
18.解:(1)35°. 4分
(2)要使CD∥AB,则∠BCD=35°. 8分
19.解:(1)∵∠EOC=98°,∴∠EOD=180°-∠EOC=82°.
∵OB平分∠EOD,∴∠BOD=∠EOD=41°. 3分
(2)∵OB平分∠EOD,∴∠BOD=∠BOE=∠DOE.
∵∠BOE∶∠EOC=1∶3,∴∠EOC=3∠BOE=3∠BOD. 5分
∵∠EOC+∠DOE=180°,∴3∠BOD+2∠BOD=180°,
解得∠BOD=36°,
∴∠AOC=∠BOD=36°. 8分
20.解:(1)证明:∵OC⊥OD,
∴∠COD=90°,
∴∠1+∠DOB=90°. 1分
∵∠D与∠1互余,
∴∠D+∠1=90°,
∴∠D=∠DOB, 2分
∴ED∥AB. 3分
(2)补全图形,如图所示. 5分
∵ED∥AB,∠OFD=65°,
∴∠AOF=∠OFD=65°. 6分
∵OF平分∠AOD,
∴∠AOD=2∠AOF=130°. 7分
∵∠COD=90°,∠AOD=∠1+∠COD,
∴∠1=40°. 8分
21.解:(1)数量关系是相等;位置关系是平行. 2分
(2)∵三角形ABC沿BC所在直线向右平移,所得的图形对应三角形DEF,
∴∠B=∠DEF,AD∥BF. 3分
∵AD∥BF,
∴∠DEF=∠ADE=60°,
∴∠B=60°. 5分
(3)∵三角形ABC以0.2 cm/s的速度沿BC所在直线向右平移,所得图形对应三角形DEF,
∴BE=0.2t. 6分
∵BE+CE=BC,
∴0.2t+1=4,
解得t=15,
即当t=15时,EC=1 cm. 9分
22.解:同位角相等,两直线平行(也可以写成同旁内角互补,两直线平行). 3分
内错角相等,两直线平行. 6分
如图所示,AB∥CD. 9分
(答案不唯一,只要摆放正确均可得分)
图1
23.解:(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;∠BEF+∠CEF. 3分
(2)证明:如图1,过点E作EF∥AB.
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠C+∠CEF=180°,∠B+∠BEF=180°,
图2
∴∠B+∠C+∠BEC=360°,
即∠B+∠C=360°-∠BEC. 7分
(3)∠1+∠3+∠5=∠2+∠4. 8分
理由:如图2,过点F作FM∥AB,则AB∥FM∥CD,
由(1)得,∠1+∠3+∠5=∠2+∠4. 12分
2
(时间:120分钟 分值:120分)
一、单项选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
1.如图,在平面内作已知直线m的垂线,可作的垂线有 ( )
A.0条 B.1条
C.2条 D.无数条
2.下面四个图形中,∠1与∠2是同位角的是 ( )
3.如图,已知直线a,b被直线c所截,下列条件不能判断a∥b的是 ( )
A.∠2=∠6
B.∠3+∠4=180°
C.∠2+∠5=180°
D.∠1=∠6
4.下列命题中,为假命题的是 ( )
A.内错角相等,两直线平行
B.同角的补角相等
C.两直线平行,同位角互补
D.过直线外一点有且只有一条直线与已知直线平行
5.如图,∠1=∠2,∠4=120°,则∠3等于 ( )
A.60°
B.40°
C.50°
D.30°
6.2022年北京冬奥会男子500米短道速滑冠军在一次直道速滑训练中,经过两次拐弯后的速滑方向与原来的方向相反,则两次拐弯的角度可能是 ( )
A.第一次向左拐52°,第二次向右拐52°
B.第一次向左拐48°,第二次向左拐48°
C.第一次向左拐73°,第二次向右拐107°
D.第一次向左拐32°,第二次向左拐148°
二、填空题(本大题共6小题,每小题3分,共18分)
7.如图,某单位要在河岸l上建一个水泵房引水到C处.他们的做法如下:过点C作CD⊥l于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是 .
8.已知直线a∥b,把一块含30°角的直角三角板按如图所示的方式放置,若∠1=48°,则∠2的度数为 .
9.如图,已知m∥n,若∠1+∠2=280°,则∠4-∠3= .
10.如图,在宽为13米、长为24米的长方形地面上修筑同样宽的道路(图中阴影部分),道路的宽为2米,余下部分种植草坪.则草坪的面积为 平方米.
11.如图,将长方形纸片ABCD沿折痕MN折叠,A,B分别落在对应位置A1,B1处,A1B1交AD于点E,若∠BNM=62°,则∠A1ME的度数为 .
12.如图,直线AB和CD交于点O,∠AOC=30°,∠BOE=90°,OF平分∠AOD.射线OE以每秒10°的速度绕点O逆时针转动,同时射线OF也以每秒4°的速度绕点O顺时针转动,当射线OE转动一周时,射线OE,OF同时停止转动.在射线OE转动一周的过程中,当OE⊥OF时,射线OE转动的时间为 秒.
三、解答题(本大题共5小题,每小题6分,共30分)
13.(1)如图,点A,O,B在同一条直线上,已知∠BOC=50°,求∠AOC的度数.
(2)如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,求∠BOD的度数.
14.如图,AD与BC交于点O,点E在OD上,∠C=∠3,∠2=70°,∠1+∠3=150°,∠A=∠D,求∠B的度数.
15.填空,并在括号内,填上推理的依据.
如图,已知∠BAE=∠E,∠B=∠D,证明:∠AFC+∠DAE=180°.
证明:∵∠BAE=∠E,
∴ ∥ ( ),
∴∠B=∠ ( ).
又∵∠B=∠D,
∴∠D=∠ (等量代换),
∴AD∥BC( ),
∴∠AFC+∠DAE=180°( ).
16.某市为了方便市民绿色出行,推出了共享单车服务.图1是某品牌共享单车放在水平地面的实物图,图2是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=54°.问当∠MAC为多少度时,AM与CB平行
17.如图,在由小正方形组成的4×4的网格中,请用无刻度直尺按下列要求作格点三角形(图形的顶点都在正方形网格的格点上).
(1)在图1中,将三角形ABC平移,得到三角形A'B'C',使得三角形A'B'C'与三角形ABC无重合部分.
(2)在图2中,线段AB与CD相交,所夹的一个角为∠α,请画一个三角形ABE,使得三角形ABE中的一个角等于∠α.
四、解答题(本大题共3小题,每小题8分,共24分)
18.如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向.
(1)∠ABC的度数为 .
(2)要使CD∥AB,则∠BCD等于多少度
19.如图,直线AB,CD相交于点O,OB平分∠EOD.
(1)若∠EOC=98°,求∠BOD的度数.
(2)若∠BOE∶∠EOC=1∶3,求∠AOC的度数.
20.如图,点O在直线AB上,OC⊥OD,∠D与∠1互余.
(1)求证:ED∥AB.
(2)OF平分∠AOD交DE于点F,若∠OFD=65°,补全图形,并求∠1的度数.
五、解答题(本大题共2小题,每小题9分,共18分)
21.如图,在三角形ABC中,BC=4 cm,将三角形ABC以0.2 cm/s的速度沿BC所在直线向右平移,所得的图形对应三角形DEF,设运动时间为t s.
(1)请直接写出AB与DE之间的关系.
(2)若∠ADE=60°,求∠B的度数.
(3)当t为何值时,EC=1 cm
22.操作探究,解决问题:
同学们玩游戏,借助两个三角形模板画平行线.
规则1:摆放一副三角板,画平行线.
小颖的做法:如图1,先画一条直线MN,之后按如图所示的方式摆放三角板,即可得到AB∥CD.她的依据是 .
小静的做法:按如图2所示的方式摆放两块三角板,也可得到AB∥CD.她的依据是 .
规则2:请你利用图3所示的两个三角形模板,将其正确摆放后画出平行线.在图4中画出你所摆放的两个三角形模板的位置.
六、解答题(本大题共12分)
23.【问题发现】(1)如图1,直线AB∥CD,连接BE,CE,可以发现∠B+∠C=∠BEC.
请把下面的证明过程补充完整:
证明:过点E作EF∥AB.
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC( ),
∴∠C=∠CEF( ).
∵EF∥AB,
∴∠B=∠BEF(同理),
∴∠B+∠C= (等量代换),
即∠B+∠C=∠BEC.
【拓展探究】(2)如果点E运动到图2所示的位置,其他条件不变,求证:∠B+∠C=360°-∠BEC.
【解决问题】(3)如图3,AB∥DC,E,F,G是AB与CD之间的点,找出∠1,∠2,∠3,∠4,∠5之间的数量关系,并说明理由.
参考答案
1.D 2.C 3.B 4.C 5.A 6.D
7.垂线段最短 8.102° 9.100° 10.242 11.56°
12.或或
提示:当OE,OF还未转动时,∠AOC=30°,∴∠AOD=150°.
∵OF平分∠AOD,∴∠AOF=∠AOD=75°,∴∠EOF=∠AOE+∠AOF=165°.
∵360÷10=36,165÷4=41.25,
∴射线OE转完一周后,射线OF还未到达原射线OE的位置.
设射线OE转动的时间为t秒.
由题意得,165-(10t+4t)=90或10t-(165-4t)=90或360-10t+165-4t=90,
解得t=或或,
∴当射线OE转动的时间为或或秒时,OE⊥OF.
13.(1)解:∠AOC=180°-50°=130°. 3分
(2)解:∠BOD=360°-90°-90°-27°=153°. 3分
14.解:∵∠C=∠3,∴BC∥EF,∴∠1+∠2=180°.
∵∠2=70°,∴∠1=110°.
∵∠1+∠3=150°,∴∠3=40°. 2分
∵∠C=∠3,∴∠C=40°.
∵∠A=∠D,∴AB∥CD,
∴∠B=∠C=40°. 6分
15.解:AB;DE;内错角相等,两直线平行; 2分
BCE;两直线平行,内错角相等; 3分
BCE; 4分
同位角相等,两直线平行; 5分
两直线平行,同旁内角互补. 6分
16.解:∵AB,CD都与地面l平行,
∴AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠BAC+∠ACB+∠BCD=180°. 3分
∵∠BCD=60°,∠BAC=54°,
∴∠ACB=66°,
∴当∠MAC=∠ACB=66°时,AM∥CB. 6分
17.解:(1)如图1,三角形A'B'C'即为所作. 3分
(2)如图2,三角形ABE即为所作,∠BAE=∠α. 6分
18.解:(1)35°. 4分
(2)要使CD∥AB,则∠BCD=35°. 8分
19.解:(1)∵∠EOC=98°,∴∠EOD=180°-∠EOC=82°.
∵OB平分∠EOD,∴∠BOD=∠EOD=41°. 3分
(2)∵OB平分∠EOD,∴∠BOD=∠BOE=∠DOE.
∵∠BOE∶∠EOC=1∶3,∴∠EOC=3∠BOE=3∠BOD. 5分
∵∠EOC+∠DOE=180°,∴3∠BOD+2∠BOD=180°,
解得∠BOD=36°,
∴∠AOC=∠BOD=36°. 8分
20.解:(1)证明:∵OC⊥OD,
∴∠COD=90°,
∴∠1+∠DOB=90°. 1分
∵∠D与∠1互余,
∴∠D+∠1=90°,
∴∠D=∠DOB, 2分
∴ED∥AB. 3分
(2)补全图形,如图所示. 5分
∵ED∥AB,∠OFD=65°,
∴∠AOF=∠OFD=65°. 6分
∵OF平分∠AOD,
∴∠AOD=2∠AOF=130°. 7分
∵∠COD=90°,∠AOD=∠1+∠COD,
∴∠1=40°. 8分
21.解:(1)数量关系是相等;位置关系是平行. 2分
(2)∵三角形ABC沿BC所在直线向右平移,所得的图形对应三角形DEF,
∴∠B=∠DEF,AD∥BF. 3分
∵AD∥BF,
∴∠DEF=∠ADE=60°,
∴∠B=60°. 5分
(3)∵三角形ABC以0.2 cm/s的速度沿BC所在直线向右平移,所得图形对应三角形DEF,
∴BE=0.2t. 6分
∵BE+CE=BC,
∴0.2t+1=4,
解得t=15,
即当t=15时,EC=1 cm. 9分
22.解:同位角相等,两直线平行(也可以写成同旁内角互补,两直线平行). 3分
内错角相等,两直线平行. 6分
如图所示,AB∥CD. 9分
(答案不唯一,只要摆放正确均可得分)
图1
23.解:(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;∠BEF+∠CEF. 3分
(2)证明:如图1,过点E作EF∥AB.
∵AB∥CD,EF∥AB,
∴EF∥CD,
∴∠C+∠CEF=180°,∠B+∠BEF=180°,
图2
∴∠B+∠C+∠BEC=360°,
即∠B+∠C=360°-∠BEC. 7分
(3)∠1+∠3+∠5=∠2+∠4. 8分
理由:如图2,过点F作FM∥AB,则AB∥FM∥CD,
由(1)得,∠1+∠3+∠5=∠2+∠4. 12分
2
