人教版小学数学五年级下册3.3.3《 长方体、正方体体积公式的应用》课件(共17张PPT)
文档属性
| 名称 | 人教版小学数学五年级下册3.3.3《 长方体、正方体体积公式的应用》课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-24 19:49:00 | ||
图片预览



文档简介
(共17张PPT)
长方体、正方体体积
公式的应用
第三单元 长方体和正方体
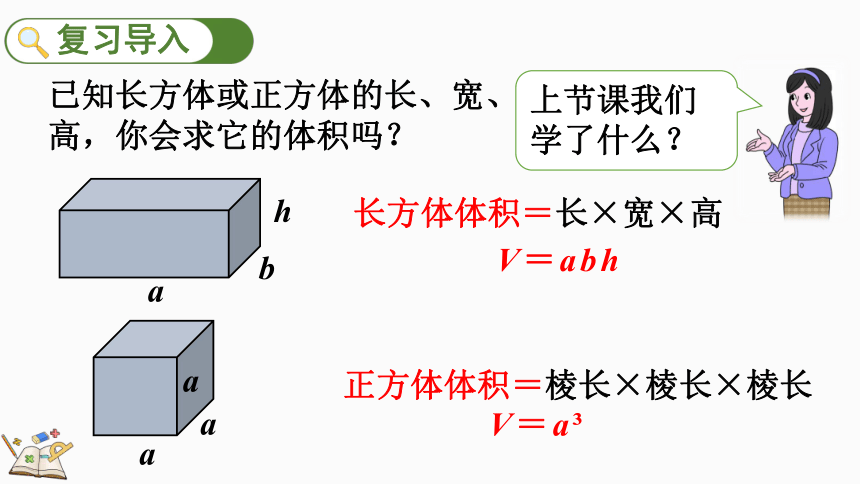
长方体体积=长×宽×高
V=abh
正方体体积=棱长×棱长×棱长
a
b
h
a
a
a
V=a
上节课我们学了什么?
已知长方体或正方体的长、宽、高,你会求它的体积吗?
1
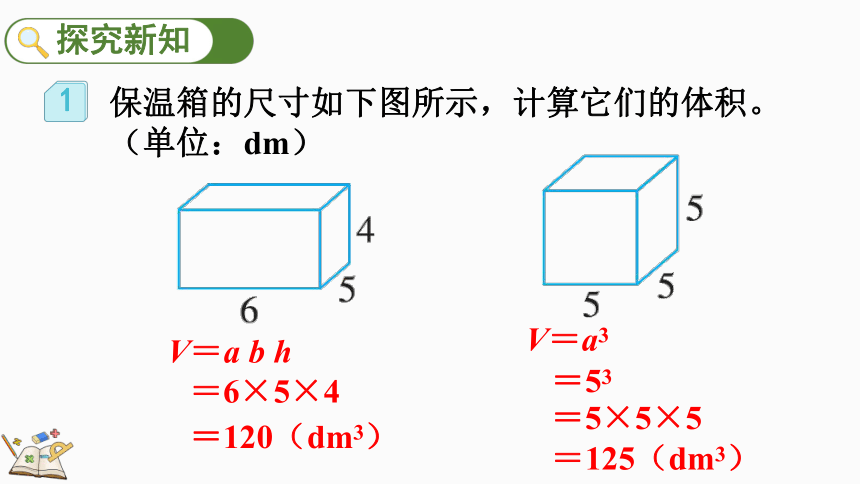
V=a b h
=6×5×4
=120(dm3)
V=a3
=53
=5×5×5
=125(dm3)
保温箱的尺寸如下图所示,计算它们的体积。(单位:dm)
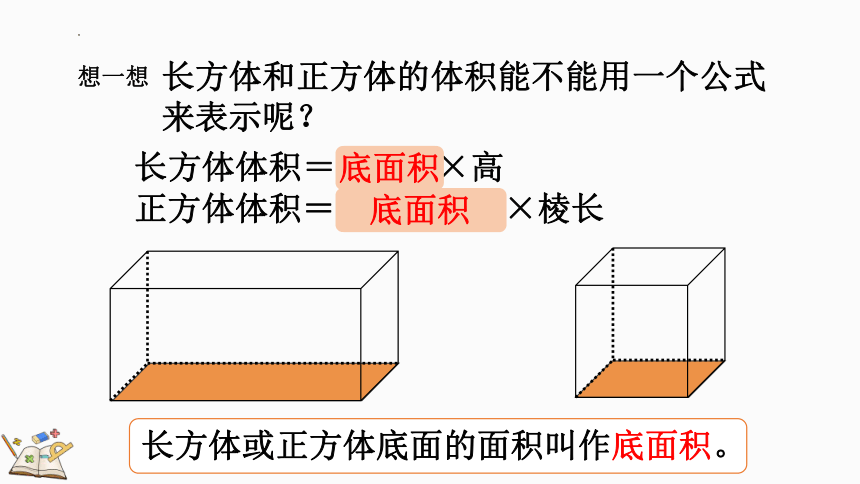
长方体和正方体的体积能不能用一个公式来表示呢?
长方体体积=长×宽×高
正方体体积=棱长×棱长×棱长
长方体或正方体底面的面积叫作底面积。
底面积
底面积
想一想
如果用S表示底面积,
长方体体积=底面积×高
正方体体积=底面积×棱长
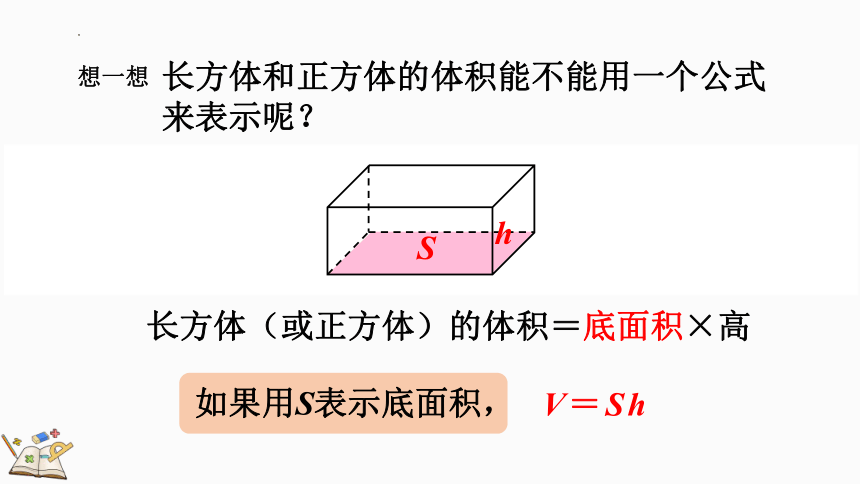
长方体(或正方体)的体积=底面积×高
V=Sh
长方体和正方体的体积能不能用一个公式来表示呢?
想一想
S
h
选自教材第31页做一做第1题
1
一块长方体豆腐的尺寸如下图所示,它的体积是多少?
15×7×5=525(cm3)
答:它的体积是525cm3。
长方体体积=长×宽×高
一根长方体木料,长5m,横截面的面积是0.06m2。这根木料的体积是多少?
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
0.06m2
长方体体积=底面积×高
选自教材第31页做一做第2题
2
选自教材第31页做一做第1题改编
3
一块长方体肥皂的尺寸如图,它的体积是多少?
15cm
7cm
8cm
长方体体积=长×宽×高
15×7×8=840(cm3)
答:它的体积是840cm3。
选自教材第31页做一做第2题改编
4
一根体积为10立方米的原木被削成了一根横截面积为1.5m2,长为6米的长方体,这根原木被削掉的体积是多少?
答:这根原木被削掉的体积是1立方米。
原木削成的长方体体积为1.5×6=9(立方米)
被削掉的体积为10 9=1(立方米)
被削掉的体积=总体积(原木的体积) 剩下的体积(长方体的体积)
计算下面图形的体积。
=15×3×20
=900(cm )
=2.5×2.5×2.5
=15.625(m )
V=abh
V=a
15cm
3cm
20cm
2.5m
2.5m
2.5m
1
一个正方体的棱长总和是108厘米,它的体积是多少?
108÷12=9(厘米)
9×9×9=729(立方厘米)
答:它的体积是729立方厘米。
正方体棱长总和=棱长×12
V=a
2
一个长方体铁块的底面积是20平方厘米,高是40厘米。把它锻造成一个截面边长是10厘米的正方形的长方体。这个长方体的高是多少?
锻造前后长方体的体积不变。
20×40=800(cm )
800÷(10×10)=8(cm)
答:锻造后的长方体的高是8cm。
V=Sh
h=V÷S
3
把两个完全一样的小长方体木块粘成一个大长方体,这个大长方体的表面积比原来两个小长方体的表面积的和减少50cm 。如果拼成的大长方体长20cm,那么一个小长方体的体积是多少立方厘米?
减少了两个侧面的面积。
一个侧面的面积:50÷2=25(cm )
小长方体的长:20÷2=10(cm)
V=Sh=25×10=250(cm )
答:一个小长方体的体积是250cm 。
4
一根铁丝长200cm,将它焊接成一个长方体模型,长是24cm,宽和高相等,这个模型的体积是多少立方厘米?
200÷4=50(cm)
宽(或高):(50 24)÷2=13(cm)
答:这个模型的体积是4056立方厘米。
体积:24×13×13=4056(cm )
这节课有什么收获呢?
长方体(或正方体)的体积=底面积×高
V=abh
S
h
长方体、正方体体积公式的应用
V=a3
V=Sh
生活中的数学
乘飞机时免费行李的尺寸限制如下图。
你知道其他交通工具关于行李尺寸的规定吗?
长方体(或正方体)的体积=底面积×高
S
h
长方体、正方体体积公式的应用
V=abh
V=a3
V=Sh
长方体、正方体体积
公式的应用
第三单元 长方体和正方体
长方体体积=长×宽×高
V=abh
正方体体积=棱长×棱长×棱长
a
b
h
a
a
a
V=a
上节课我们学了什么?
已知长方体或正方体的长、宽、高,你会求它的体积吗?
1
V=a b h
=6×5×4
=120(dm3)
V=a3
=53
=5×5×5
=125(dm3)
保温箱的尺寸如下图所示,计算它们的体积。(单位:dm)
长方体和正方体的体积能不能用一个公式来表示呢?
长方体体积=长×宽×高
正方体体积=棱长×棱长×棱长
长方体或正方体底面的面积叫作底面积。
底面积
底面积
想一想
如果用S表示底面积,
长方体体积=底面积×高
正方体体积=底面积×棱长
长方体(或正方体)的体积=底面积×高
V=Sh
长方体和正方体的体积能不能用一个公式来表示呢?
想一想
S
h
选自教材第31页做一做第1题
1
一块长方体豆腐的尺寸如下图所示,它的体积是多少?
15×7×5=525(cm3)
答:它的体积是525cm3。
长方体体积=长×宽×高
一根长方体木料,长5m,横截面的面积是0.06m2。这根木料的体积是多少?
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
0.06m2
长方体体积=底面积×高
选自教材第31页做一做第2题
2
选自教材第31页做一做第1题改编
3
一块长方体肥皂的尺寸如图,它的体积是多少?
15cm
7cm
8cm
长方体体积=长×宽×高
15×7×8=840(cm3)
答:它的体积是840cm3。
选自教材第31页做一做第2题改编
4
一根体积为10立方米的原木被削成了一根横截面积为1.5m2,长为6米的长方体,这根原木被削掉的体积是多少?
答:这根原木被削掉的体积是1立方米。
原木削成的长方体体积为1.5×6=9(立方米)
被削掉的体积为10 9=1(立方米)
被削掉的体积=总体积(原木的体积) 剩下的体积(长方体的体积)
计算下面图形的体积。
=15×3×20
=900(cm )
=2.5×2.5×2.5
=15.625(m )
V=abh
V=a
15cm
3cm
20cm
2.5m
2.5m
2.5m
1
一个正方体的棱长总和是108厘米,它的体积是多少?
108÷12=9(厘米)
9×9×9=729(立方厘米)
答:它的体积是729立方厘米。
正方体棱长总和=棱长×12
V=a
2
一个长方体铁块的底面积是20平方厘米,高是40厘米。把它锻造成一个截面边长是10厘米的正方形的长方体。这个长方体的高是多少?
锻造前后长方体的体积不变。
20×40=800(cm )
800÷(10×10)=8(cm)
答:锻造后的长方体的高是8cm。
V=Sh
h=V÷S
3
把两个完全一样的小长方体木块粘成一个大长方体,这个大长方体的表面积比原来两个小长方体的表面积的和减少50cm 。如果拼成的大长方体长20cm,那么一个小长方体的体积是多少立方厘米?
减少了两个侧面的面积。
一个侧面的面积:50÷2=25(cm )
小长方体的长:20÷2=10(cm)
V=Sh=25×10=250(cm )
答:一个小长方体的体积是250cm 。
4
一根铁丝长200cm,将它焊接成一个长方体模型,长是24cm,宽和高相等,这个模型的体积是多少立方厘米?
200÷4=50(cm)
宽(或高):(50 24)÷2=13(cm)
答:这个模型的体积是4056立方厘米。
体积:24×13×13=4056(cm )
这节课有什么收获呢?
长方体(或正方体)的体积=底面积×高
V=abh
S
h
长方体、正方体体积公式的应用
V=a3
V=Sh
生活中的数学
乘飞机时免费行李的尺寸限制如下图。
你知道其他交通工具关于行李尺寸的规定吗?
长方体(或正方体)的体积=底面积×高
S
h
长方体、正方体体积公式的应用
V=abh
V=a3
V=Sh
