第十八章 平行四边形 单元练习(含答案) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 第十八章 平行四边形 单元练习(含答案) 2023-2024学年初中数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 307.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-25 22:41:09 | ||
图片预览




文档简介
第十八章 平行四边形
(时间:120分钟 满分:120分)
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
1.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是 ( )
A.AB∥DC,AD∥BC
B.AB=DC,AD=BC
C.AO=CO,BO=DO
D.AB∥DC,AD=BC
2.如图,矩形OABC的顶点B的坐标为(2,3),则AC的长为 ( )
A.
B.
C.5
D.4
3.菱形具有,而矩形不具有的性质是 ( )
A.对角线互相平分 B.四条边都相等
C.对角相等 D.邻角互补
4.如图,将 ABCD沿对角线AC折叠,点B落在点B'处,若∠1=∠2=48°,则∠B的度数为 ( )
A.98°
B.108°
C.118°
D.72°
5.如图,四边形ABCD是正方形,AB=1,F为对角线AC延长线上一点,以BC,CF为邻边作菱形BEFC,连接DE,则DE的长是 ( )
A.
B.1+
C.
D.2
6.如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于点M,O,N,连接AN,CM,则四边形ANCM是菱形;
乙:分别作∠DAB,∠ABC的平分线AE,BF,分别交BC,AD于点E,F,连接EF,则四边形ABEF是菱形.根据两人的作法可判断 ( )
A.甲正确,乙错误 B.乙正确,甲错误
C.甲、乙均正确 D.甲、乙均错误
二、填空题(本大题共6小题,每小题3分,共18分)
7.如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 ,使ABCD成为菱形(只需添加一个即可).
8.如图,在 ABCD中,已知AD⊥DB,AC=10,AD=4,则BD的长是 .
9.如图,O为矩形ABCD的对角线交点,∠AOB=2∠BOC,对角线AC=12,则CB= .
10.如图,正方形ABCD的周长为 8 cm,则矩形EFBG中EF+FB的长为 cm.
11.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为BC边上一动点,PE⊥AB于点E,PF⊥AC于点F,连接EF,M为EF的中点,则AM的最小值为 .
12.已知平面直角坐标系中有四个点:A(1,1),B(3,1),C(2,3),D,若以它们为顶点的四边形是平行四边形,则点D的坐标为 .
三、(本大题共5小题,每小题6分,共30分)
13.(1)如图,四边形ABCD是菱形,过点A作AE⊥BC于点E,AF⊥CD于点F.求证:BE=DF.
(2)如图,矩形ABCD的对角线AC,BD交于点O,E是AD的中点,连接OE.若OE=3,AD=8,求对角线AC的长.
14.如图,在平行四边形ABCD中,点E,F分别在AD,BC边上,且∠ABE=∠CDF.求证:四边形BFDE是平行四边形.
15.如图,在△ABC中,点D在BC上,且DC=AC,CE⊥AD于点E,F是AB的中点.求证:EF∥BC.
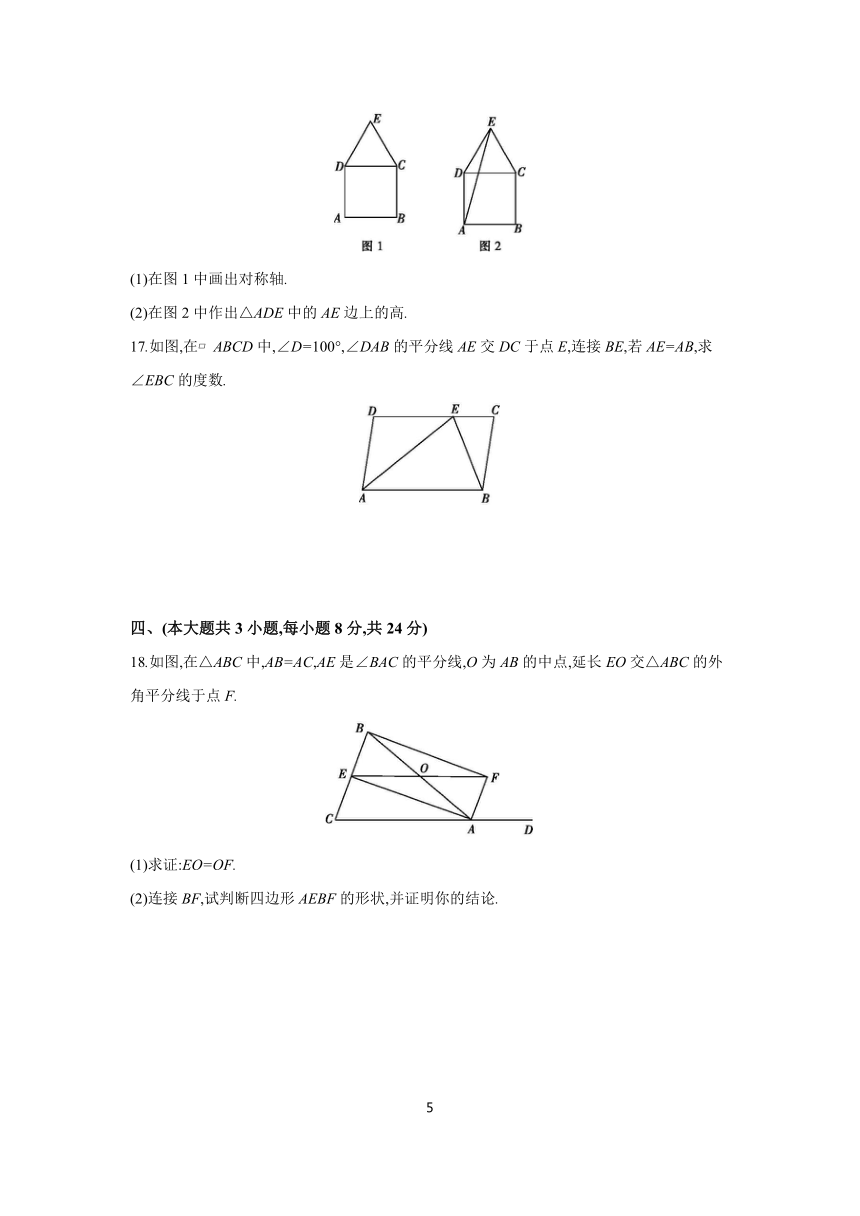
16.如图,已知正方形ABCD和等边三角形CDE.请按要求完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
(1)在图1中画出对称轴.
(2)在图2中作出△ADE中的AE边上的高.
17.如图,在 ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE,若AE=AB,求∠EBC的度数.
四、(本大题共3小题,每小题8分,共24分)
18.如图,在△ABC中,AB=AC,AE是∠BAC的平分线,O为AB的中点,延长EO交△ABC的外角平分线于点F.
(1)求证:EO=OF.
(2)连接BF,试判断四边形AEBF的形状,并证明你的结论.
19.如图,平行四边形ABCD的对角线AC,BD交于点O,过点C,D分别作CF∥BD,DF∥AC,连接BF交AC于点E.
(1)求证:△FCE≌△BOE.
(2)当∠ADC=90°时,判断四边形OCFD的形状,并说明理由.
20.如图,四边形ABCD的对角线AC⊥BD且相交于点E,F为四边形ABCD外一点,且∠FCA=90°,BC平分∠DBF,∠CBF=∠DCB.求证:四边形DBFC是菱形.
五、(本大题共2小题,每小题9分,共18分)
21.如图,E,F是 ABCD的对角线AC上的两点,且AE=CF,连接BE,BF,DE,DF.
(1)求证:四边形BEDF是平行四边形.
(2)若AB⊥BF,AB=4,BF=3,AC=8.
①线段EF长为 .
②求四边形BEDF的面积.
22.如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连接DE并延长交射线AB于点F,连接BE.
(1)如图1,求证:∠AFD=∠EBC.
(2)如图2,若DE=EC,且BE⊥AF,求∠DAB的度数.
(3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数.(只写出条件与对应的结果)
六、(本大题共12分)
23.如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是 ,位置关系是 .
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立 请作出判断并给予证明.
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗 请直接作出判断,不必说明理由.
参考答案
1.D 2.A 3.B 4.B 5.C 6.C
7.答案不唯一,如OA=OC或AB∥CD等.
提示:由于对角线已垂直,所以添加的条件能使四边形ABCD为平行四边形即可.
8.6 9.6 10.2 11.
12.(4,3)或(0,3)或(2,-1) 提示:如图,分三种情况:
①当BC为对角线时,点D的坐标为(4,3);
②当AC为对角线时,点D的坐标为(0,3);
③当AB为对角线时,点D的坐标为(2,-1).
综上所述,点D的坐标为(4,3)或(0,3)或(2,-1).
13.(1)证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D.
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°. 1分
在△ABE和△ADF中,
∴△ABE≌△ADF(AAS), 2分
∴BE=DF. 3分
(2)解:∵矩形ABCD,∴OB=OD.
∵E是AD的中点,∴AE=DE,
∴OE=AB. 1分
∵OE=3,∴AB=6. 2分
∵AD=8,∠DAB=90°,∴BD=10.
∵矩形ABCD,∴AC=BD=10. 3分
14.证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB=CD. 1分
在△ABE和△CDF中,
∴△ABE≌△CDF(ASA), 3分
∴AE=CF,BE=DF. 4分
∵AD=CB,
∴AD-AE=BC-CF,
即DE=BF,
∴四边形BFDE是平行四边形. 6分
15.证明:∵DC=AC,CE⊥AD于点E,
∴AE=ED. 2分
∵F是AB的中点,
∴AF=FB, 4分
∴EF为△ABD的中位线,
∴EF∥BC. 6分
16.解:(1)如图1,直线OE就是所求的对称轴. 3分
(2)如图2,线段DF就是所求的高(提示:连接以AE为底边的两个等腰三角形的顶点,交AE于点F). 6分
17.解:∵四边形ABCD是平行四边形,
∴AB∥DC,∠ABC=∠D, 1分
∴∠DAB+∠D=180°. 2分
∵∠D=100°,
∴∠DAB=80°,∠ABC=100°. 3分
又∵∠DAB的平分线交DC于点E,
∴∠EAD=∠EAB=40°.
∵AE=AB,
∴∠ABE=×(180°-40°)=70°, 5分
∴∠EBC=∠ABC-∠ABE=100°-70°=30°. 6分
18.解:(1)证明:∵AB=AC,AE是∠BAC的平分线,
∴CE=BE,∠AEB=90°.
∵O是AB的中点,
∴EO是△ABC的中位线,EO=AO=BO,∴∠EBO=∠BEO.
又∵∠EBO=∠BCA,∴∠BEO=∠BCA,
∴EO∥AC,
∴∠EFA=∠FAD.
∵AF平分∠BAD,
∴∠FAD=∠FAB,
∴∠FAB=∠EFA,
∴OF=AO,
∴EO=OF. 5分
(2)四边形AEBF是矩形. 6分
证明:∵AO=BO,EO=FO,
∴四边形AEBF是平行四边形.
又∵∠AEB=90°,
∴四边形AEBF是矩形. 8分
19.解:(1)证明:∵CF∥BD,DF∥AC,
∴四边形OCFD是平行四边形,∠OBE=∠CFE,
∴OD=CF.
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OB=CF.
在△FCE和△BOE中,
∴△FCE≌△BOE(AAS). 4分
(2)当∠ADC=90°时,四边形OCFD为菱形. 5分
理由如下:
∵∠ADC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OC=OD.
∵四边形OCFD是平行四边形,
∴四边形OCFD为菱形. 8分
20.证明:∵AC⊥BD,∠FCA=90°,
∴∠AEB=∠ACF,
∴BD∥CF. 2分
∵∠CBF=∠DCB,
∴CD∥BF,
∴四边形DBFC是平行四边形. 4分
∵BC平分∠DBF,
∴∠CBF=∠CBD. 5分
∵∠CBF=∠DCB,
∴∠CBD=∠DCB,
∴CD=BD, 7分
∴四边形DBFC是菱形. 8分
21.解:(1)证明:如图1,连接BD,BD交AC于点O.
图1
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵AE=CF,
∴OE=OF,
又∵OB=OD,
∴四边形BEDF是平行四边形. 3分
(2)①2. 5分
提示:在Rt△ABF中,AF===5,
∵AC=8,
∴CF=AC-AF=8-5=3.
∵AE=CF=3,
∴EF=AF-AE=2.
②如图2,过点B作BH⊥AF于点H,
图2
∵AB⊥BF,AB=4,BF=3,∴AF=5,
∴S△ABF=AB·BF=AF·BH,
∴3×4=5BH,解得BH=.
∵四边形BEDF是平行四边形,
∴BE=DF,BF=DE.
在△BEF和△DFE中,
∴△BEF≌△DFE(SSS),
∴S△BEF=S△DFE,
∴S四边形BEDF=2S△BEF=2××2×=. 9分
22.解:(1)证明:∵四边形ABCD是菱形,
∴CD=CB,∠ACD=∠ACB.
在△DCE和△BCE中,
∴△DCE≌△BCE,∴∠CDE=∠CBE. 2分
∵CD∥AB,∴∠CDE=∠AFD,
∴∠EBC=∠AFD. 3分
(2)∵四边形ABCD是菱形,
∴AD=AB,∠DAC=∠BAC.
又∵AC=AC,∴△DAE≌△BAE,
∴∠ADE=∠ABE.
∵BE⊥AF,∴∠ADE=∠ABE=90°.
∵ED=EC,∴∠EDC=∠ECD.
∵AD=CD,∴∠DAC=∠DCA,
∴∠DAC=∠ACD=∠CDE. 5分
设∠DAC=x,
在△ADC中,x+x+90°+x=180°,
解得x=30°,∴∠DAB=2x=60°,
即∠DAB的度数为60°. 6分
(3)分下列两种情况:
①如图1,当点F在AB延长线上时,
∵∠EBF为钝角,
∴只能是BE=BF,设∠BEF=∠BFE=x°,
由(1)可知∠EBC=∠AFD=x°,
∴∠EBF=(90+x)°.
在△EBF中,有90+x+x+x=180,
解得x=30,∴∠EFB=30°;
②如图2,当点F在线段AB上时,
∵∠EFB为钝角,
∴只能是FE=FB,设∠BEF=∠EBF=x°,则有∠AFD=2x°.
∵∠EBC=∠AFD,
∠EBC+∠EBF=90°,
∠AFD+∠ADF=90°,
∴∠ADF=∠EBF=x°.
在Rt△ADF中,有x+2x=90,
解得x=30,∴∠EFB=180°-2x°=120°.
综上所述,当F在AB的延长线上时,∠EFB=30°,当F在线段AB上时,∠EFB=120°. 9分
23.解:(1)AF=BE;AF⊥BE. 4分
(2)结论仍然成立. 5分
证明:设AF,BE相交于点M.
∵EA=ED=FD=FC,AD=CD,
∴△ADE≌△DCF(SSS), 6分
∴∠DAE=∠CDF.
∵∠BAD=∠CDA=90°,∴∠BAE=∠ADF.
又∵AB=DA,AE=DF,
∴△ABE≌△DAF(SAS),
∴BE=AF,∠ABM=∠DAF. 8分
又∵∠BAD=∠DAF+∠BAM=90°,
∴∠ABM+∠BAM=90°,
∴∠AMB=180°-(∠ABM+∠BAM)=90°,∴BE⊥AF. 9分
(3)第(1)问中的结论都能成立. 12分
2
(时间:120分钟 满分:120分)
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
1.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是 ( )
A.AB∥DC,AD∥BC
B.AB=DC,AD=BC
C.AO=CO,BO=DO
D.AB∥DC,AD=BC
2.如图,矩形OABC的顶点B的坐标为(2,3),则AC的长为 ( )
A.
B.
C.5
D.4
3.菱形具有,而矩形不具有的性质是 ( )
A.对角线互相平分 B.四条边都相等
C.对角相等 D.邻角互补
4.如图,将 ABCD沿对角线AC折叠,点B落在点B'处,若∠1=∠2=48°,则∠B的度数为 ( )
A.98°
B.108°
C.118°
D.72°
5.如图,四边形ABCD是正方形,AB=1,F为对角线AC延长线上一点,以BC,CF为邻边作菱形BEFC,连接DE,则DE的长是 ( )
A.
B.1+
C.
D.2
6.如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于点M,O,N,连接AN,CM,则四边形ANCM是菱形;
乙:分别作∠DAB,∠ABC的平分线AE,BF,分别交BC,AD于点E,F,连接EF,则四边形ABEF是菱形.根据两人的作法可判断 ( )
A.甲正确,乙错误 B.乙正确,甲错误
C.甲、乙均正确 D.甲、乙均错误
二、填空题(本大题共6小题,每小题3分,共18分)
7.如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 ,使ABCD成为菱形(只需添加一个即可).
8.如图,在 ABCD中,已知AD⊥DB,AC=10,AD=4,则BD的长是 .
9.如图,O为矩形ABCD的对角线交点,∠AOB=2∠BOC,对角线AC=12,则CB= .
10.如图,正方形ABCD的周长为 8 cm,则矩形EFBG中EF+FB的长为 cm.
11.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为BC边上一动点,PE⊥AB于点E,PF⊥AC于点F,连接EF,M为EF的中点,则AM的最小值为 .
12.已知平面直角坐标系中有四个点:A(1,1),B(3,1),C(2,3),D,若以它们为顶点的四边形是平行四边形,则点D的坐标为 .
三、(本大题共5小题,每小题6分,共30分)
13.(1)如图,四边形ABCD是菱形,过点A作AE⊥BC于点E,AF⊥CD于点F.求证:BE=DF.
(2)如图,矩形ABCD的对角线AC,BD交于点O,E是AD的中点,连接OE.若OE=3,AD=8,求对角线AC的长.
14.如图,在平行四边形ABCD中,点E,F分别在AD,BC边上,且∠ABE=∠CDF.求证:四边形BFDE是平行四边形.
15.如图,在△ABC中,点D在BC上,且DC=AC,CE⊥AD于点E,F是AB的中点.求证:EF∥BC.
16.如图,已知正方形ABCD和等边三角形CDE.请按要求完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
(1)在图1中画出对称轴.
(2)在图2中作出△ADE中的AE边上的高.
17.如图,在 ABCD中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE,若AE=AB,求∠EBC的度数.
四、(本大题共3小题,每小题8分,共24分)
18.如图,在△ABC中,AB=AC,AE是∠BAC的平分线,O为AB的中点,延长EO交△ABC的外角平分线于点F.
(1)求证:EO=OF.
(2)连接BF,试判断四边形AEBF的形状,并证明你的结论.
19.如图,平行四边形ABCD的对角线AC,BD交于点O,过点C,D分别作CF∥BD,DF∥AC,连接BF交AC于点E.
(1)求证:△FCE≌△BOE.
(2)当∠ADC=90°时,判断四边形OCFD的形状,并说明理由.
20.如图,四边形ABCD的对角线AC⊥BD且相交于点E,F为四边形ABCD外一点,且∠FCA=90°,BC平分∠DBF,∠CBF=∠DCB.求证:四边形DBFC是菱形.
五、(本大题共2小题,每小题9分,共18分)
21.如图,E,F是 ABCD的对角线AC上的两点,且AE=CF,连接BE,BF,DE,DF.
(1)求证:四边形BEDF是平行四边形.
(2)若AB⊥BF,AB=4,BF=3,AC=8.
①线段EF长为 .
②求四边形BEDF的面积.
22.如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连接DE并延长交射线AB于点F,连接BE.
(1)如图1,求证:∠AFD=∠EBC.
(2)如图2,若DE=EC,且BE⊥AF,求∠DAB的度数.
(3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数.(只写出条件与对应的结果)
六、(本大题共12分)
23.如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是 ,位置关系是 .
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立 请作出判断并给予证明.
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗 请直接作出判断,不必说明理由.
参考答案
1.D 2.A 3.B 4.B 5.C 6.C
7.答案不唯一,如OA=OC或AB∥CD等.
提示:由于对角线已垂直,所以添加的条件能使四边形ABCD为平行四边形即可.
8.6 9.6 10.2 11.
12.(4,3)或(0,3)或(2,-1) 提示:如图,分三种情况:
①当BC为对角线时,点D的坐标为(4,3);
②当AC为对角线时,点D的坐标为(0,3);
③当AB为对角线时,点D的坐标为(2,-1).
综上所述,点D的坐标为(4,3)或(0,3)或(2,-1).
13.(1)证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D.
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°. 1分
在△ABE和△ADF中,
∴△ABE≌△ADF(AAS), 2分
∴BE=DF. 3分
(2)解:∵矩形ABCD,∴OB=OD.
∵E是AD的中点,∴AE=DE,
∴OE=AB. 1分
∵OE=3,∴AB=6. 2分
∵AD=8,∠DAB=90°,∴BD=10.
∵矩形ABCD,∴AC=BD=10. 3分
14.证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB=CD. 1分
在△ABE和△CDF中,
∴△ABE≌△CDF(ASA), 3分
∴AE=CF,BE=DF. 4分
∵AD=CB,
∴AD-AE=BC-CF,
即DE=BF,
∴四边形BFDE是平行四边形. 6分
15.证明:∵DC=AC,CE⊥AD于点E,
∴AE=ED. 2分
∵F是AB的中点,
∴AF=FB, 4分
∴EF为△ABD的中位线,
∴EF∥BC. 6分
16.解:(1)如图1,直线OE就是所求的对称轴. 3分
(2)如图2,线段DF就是所求的高(提示:连接以AE为底边的两个等腰三角形的顶点,交AE于点F). 6分
17.解:∵四边形ABCD是平行四边形,
∴AB∥DC,∠ABC=∠D, 1分
∴∠DAB+∠D=180°. 2分
∵∠D=100°,
∴∠DAB=80°,∠ABC=100°. 3分
又∵∠DAB的平分线交DC于点E,
∴∠EAD=∠EAB=40°.
∵AE=AB,
∴∠ABE=×(180°-40°)=70°, 5分
∴∠EBC=∠ABC-∠ABE=100°-70°=30°. 6分
18.解:(1)证明:∵AB=AC,AE是∠BAC的平分线,
∴CE=BE,∠AEB=90°.
∵O是AB的中点,
∴EO是△ABC的中位线,EO=AO=BO,∴∠EBO=∠BEO.
又∵∠EBO=∠BCA,∴∠BEO=∠BCA,
∴EO∥AC,
∴∠EFA=∠FAD.
∵AF平分∠BAD,
∴∠FAD=∠FAB,
∴∠FAB=∠EFA,
∴OF=AO,
∴EO=OF. 5分
(2)四边形AEBF是矩形. 6分
证明:∵AO=BO,EO=FO,
∴四边形AEBF是平行四边形.
又∵∠AEB=90°,
∴四边形AEBF是矩形. 8分
19.解:(1)证明:∵CF∥BD,DF∥AC,
∴四边形OCFD是平行四边形,∠OBE=∠CFE,
∴OD=CF.
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OB=CF.
在△FCE和△BOE中,
∴△FCE≌△BOE(AAS). 4分
(2)当∠ADC=90°时,四边形OCFD为菱形. 5分
理由如下:
∵∠ADC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OC=OD.
∵四边形OCFD是平行四边形,
∴四边形OCFD为菱形. 8分
20.证明:∵AC⊥BD,∠FCA=90°,
∴∠AEB=∠ACF,
∴BD∥CF. 2分
∵∠CBF=∠DCB,
∴CD∥BF,
∴四边形DBFC是平行四边形. 4分
∵BC平分∠DBF,
∴∠CBF=∠CBD. 5分
∵∠CBF=∠DCB,
∴∠CBD=∠DCB,
∴CD=BD, 7分
∴四边形DBFC是菱形. 8分
21.解:(1)证明:如图1,连接BD,BD交AC于点O.
图1
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵AE=CF,
∴OE=OF,
又∵OB=OD,
∴四边形BEDF是平行四边形. 3分
(2)①2. 5分
提示:在Rt△ABF中,AF===5,
∵AC=8,
∴CF=AC-AF=8-5=3.
∵AE=CF=3,
∴EF=AF-AE=2.
②如图2,过点B作BH⊥AF于点H,
图2
∵AB⊥BF,AB=4,BF=3,∴AF=5,
∴S△ABF=AB·BF=AF·BH,
∴3×4=5BH,解得BH=.
∵四边形BEDF是平行四边形,
∴BE=DF,BF=DE.
在△BEF和△DFE中,
∴△BEF≌△DFE(SSS),
∴S△BEF=S△DFE,
∴S四边形BEDF=2S△BEF=2××2×=. 9分
22.解:(1)证明:∵四边形ABCD是菱形,
∴CD=CB,∠ACD=∠ACB.
在△DCE和△BCE中,
∴△DCE≌△BCE,∴∠CDE=∠CBE. 2分
∵CD∥AB,∴∠CDE=∠AFD,
∴∠EBC=∠AFD. 3分
(2)∵四边形ABCD是菱形,
∴AD=AB,∠DAC=∠BAC.
又∵AC=AC,∴△DAE≌△BAE,
∴∠ADE=∠ABE.
∵BE⊥AF,∴∠ADE=∠ABE=90°.
∵ED=EC,∴∠EDC=∠ECD.
∵AD=CD,∴∠DAC=∠DCA,
∴∠DAC=∠ACD=∠CDE. 5分
设∠DAC=x,
在△ADC中,x+x+90°+x=180°,
解得x=30°,∴∠DAB=2x=60°,
即∠DAB的度数为60°. 6分
(3)分下列两种情况:
①如图1,当点F在AB延长线上时,
∵∠EBF为钝角,
∴只能是BE=BF,设∠BEF=∠BFE=x°,
由(1)可知∠EBC=∠AFD=x°,
∴∠EBF=(90+x)°.
在△EBF中,有90+x+x+x=180,
解得x=30,∴∠EFB=30°;
②如图2,当点F在线段AB上时,
∵∠EFB为钝角,
∴只能是FE=FB,设∠BEF=∠EBF=x°,则有∠AFD=2x°.
∵∠EBC=∠AFD,
∠EBC+∠EBF=90°,
∠AFD+∠ADF=90°,
∴∠ADF=∠EBF=x°.
在Rt△ADF中,有x+2x=90,
解得x=30,∴∠EFB=180°-2x°=120°.
综上所述,当F在AB的延长线上时,∠EFB=30°,当F在线段AB上时,∠EFB=120°. 9分
23.解:(1)AF=BE;AF⊥BE. 4分
(2)结论仍然成立. 5分
证明:设AF,BE相交于点M.
∵EA=ED=FD=FC,AD=CD,
∴△ADE≌△DCF(SSS), 6分
∴∠DAE=∠CDF.
∵∠BAD=∠CDA=90°,∴∠BAE=∠ADF.
又∵AB=DA,AE=DF,
∴△ABE≌△DAF(SAS),
∴BE=AF,∠ABM=∠DAF. 8分
又∵∠BAD=∠DAF+∠BAM=90°,
∴∠ABM+∠BAM=90°,
∴∠AMB=180°-(∠ABM+∠BAM)=90°,∴BE⊥AF. 9分
(3)第(1)问中的结论都能成立. 12分
2
