7.4平行线的判定导学案
图片预览
文档简介
课题:7.4平行线的判定
学习目标 1.掌握平行线的判定定理,并会用判定定理判定两直线平行;2.积极参与合作交流,初步体会“推理”的意义。
重点 第二、三个判定方法的发现、说理和应用.
难点 问题的思考和推理过程。
教学过程
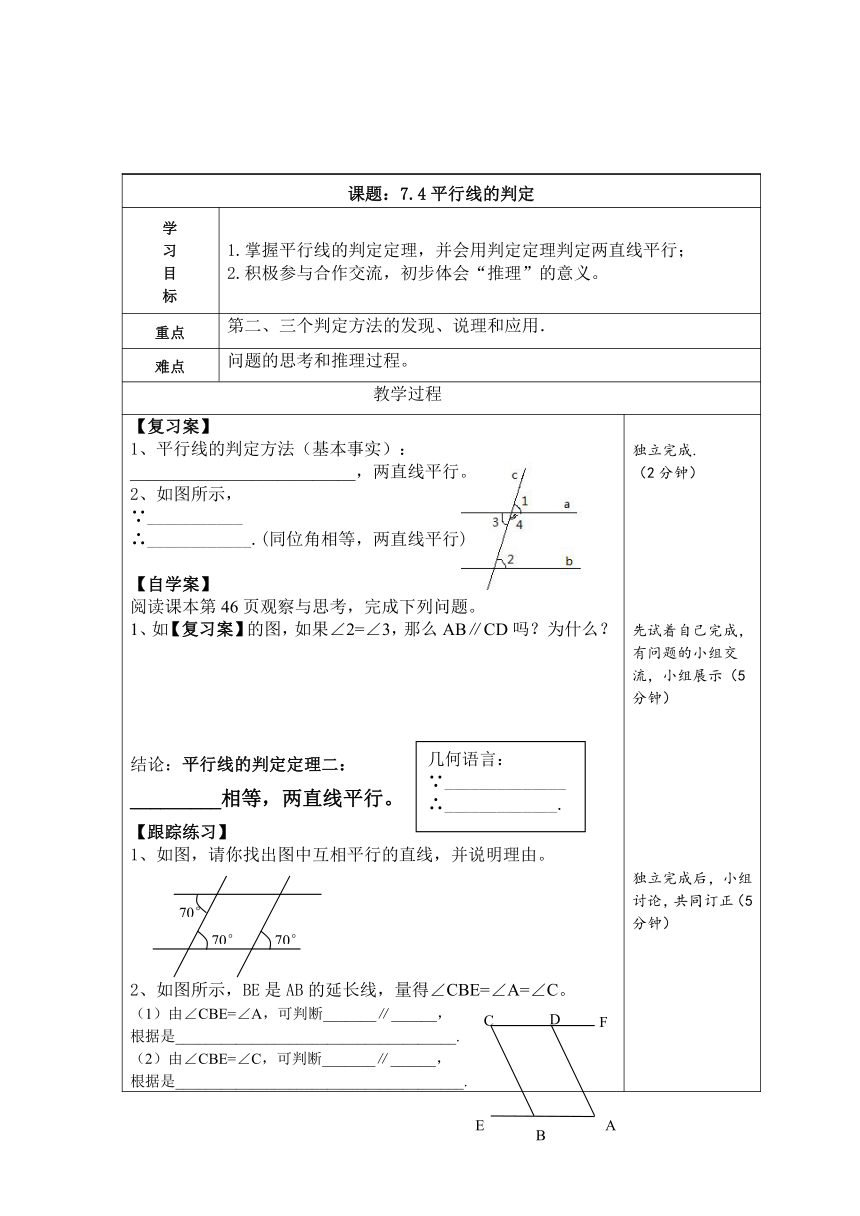
【复习案】1、平行线的判定方法(基本事实):__________________________,两直线平行。2、如图所示,∵___________∴____________.(同位角相等,两直线平行)【自学案】阅读课本第46页观察与思考,完成下列问题。1、如【复习案】的图,如果∠2=∠3,那么AB∥CD吗?为什么?结论:平行线的判定定理二:_________相等,两直线平行。【跟踪练习】1、如图,请你找出图中互相平行的直线,并说明理由。2、如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C。(1)由∠CBE=∠A,可判断_______∥______,根据是_____________________________________.(2)由∠CBE=∠C,可判断_______∥______,根据是______________________________________.【探究案】2、还如【复习案】的图,如果∠2+∠4=180°,那么AB∥CD吗?为什么?结论:平行线的判定定理三:___________互补,两直线平行。例题、如图,已知直线AB,CD被直线EF所截, ∠1=60°,∠2=120°。对AB∥CD说明理由。你还有其它方法吗 【总结与反思】【训练案】文字叙述符号语言图形 相等,两直线平行。∵ ∴a∥b 相等,两直线平行。∵ ∴a∥b 互补,两直线平行。∵ ∴a∥b 1、总结平行线的判定方法,填表。2、如图∵∠1=∠2,∴_______∥________( ) ∵∠3=∠4,∴_______∥________( )3、如图,当∠________=∠_________时,AD∥BC,当∠_______=∠_________时,AB∥CD。【感悟反思】知识点总结:我的感悟:我的疑难:【检测案】1、如图⑦,∠D=∠EFC,那么( )A.AD∥BC B.AB∥CD C.EF∥BC D.AD∥EF2、如图⑧,判定AB∥EC的理由是( )A.∠B=∠ACE B.∠A=∠ECD C.∠B=∠ACB D.∠A=∠ACE3、如图⑨,下列推理正确的是( )A.∵∠1=∠3,∴∥ B.∵∠1=∠2,∴∥ C.∵∠1=∠2,∴ ∥ D.∵∠1=∠5,∴∥4、已知,如图∠1+∠2=180°,填空。 ∵∠1+∠2=180°( )又∵∠2=∠3( )∴∠1+∠3=180°∴_________( )5、如图,在四边形ABCD中,已知∠B=60°,∠C=120°,AB与CD平行吗? AD与BC平行吗? ( http: / / www.21cnjy.com ) 独立完成. (2分钟)先试着自己完成,有问题的小组交流,小组展示(5分钟)独立完成后,小组讨论,共同订正(5分钟)先试着自己完成,有问题的小组交流,小组展示(6分钟)认真读题,首先自己仔细分析,解决问题,然后与对子交流对照。(5分钟)自己总结(1分钟)要求先独立思考,自主完成,再与对子交流互查(4分钟) 学生独立完成,给学生发言的机会。注意规范学生过程的书写。
几何语言:
∵______________
∴_____________.
70°
70°
70°
C
D
E
B
A
F
几何语言:
∵________________
∴_______________.
A
1
2
B
C
D
F
E
学习目标 1.掌握平行线的判定定理,并会用判定定理判定两直线平行;2.积极参与合作交流,初步体会“推理”的意义。
重点 第二、三个判定方法的发现、说理和应用.
难点 问题的思考和推理过程。
教学过程
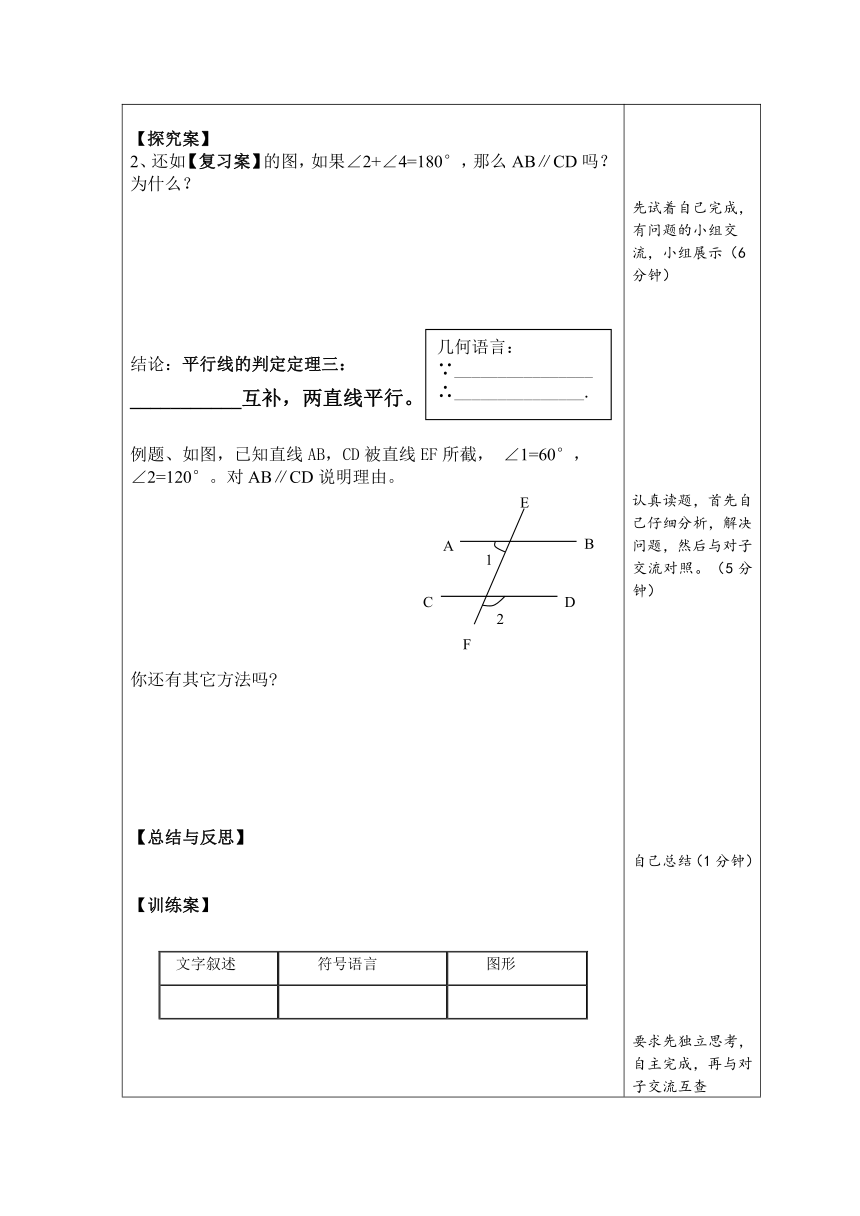
【复习案】1、平行线的判定方法(基本事实):__________________________,两直线平行。2、如图所示,∵___________∴____________.(同位角相等,两直线平行)【自学案】阅读课本第46页观察与思考,完成下列问题。1、如【复习案】的图,如果∠2=∠3,那么AB∥CD吗?为什么?结论:平行线的判定定理二:_________相等,两直线平行。【跟踪练习】1、如图,请你找出图中互相平行的直线,并说明理由。2、如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C。(1)由∠CBE=∠A,可判断_______∥______,根据是_____________________________________.(2)由∠CBE=∠C,可判断_______∥______,根据是______________________________________.【探究案】2、还如【复习案】的图,如果∠2+∠4=180°,那么AB∥CD吗?为什么?结论:平行线的判定定理三:___________互补,两直线平行。例题、如图,已知直线AB,CD被直线EF所截, ∠1=60°,∠2=120°。对AB∥CD说明理由。你还有其它方法吗 【总结与反思】【训练案】文字叙述符号语言图形 相等,两直线平行。∵ ∴a∥b 相等,两直线平行。∵ ∴a∥b 互补,两直线平行。∵ ∴a∥b 1、总结平行线的判定方法,填表。2、如图∵∠1=∠2,∴_______∥________( ) ∵∠3=∠4,∴_______∥________( )3、如图,当∠________=∠_________时,AD∥BC,当∠_______=∠_________时,AB∥CD。【感悟反思】知识点总结:我的感悟:我的疑难:【检测案】1、如图⑦,∠D=∠EFC,那么( )A.AD∥BC B.AB∥CD C.EF∥BC D.AD∥EF2、如图⑧,判定AB∥EC的理由是( )A.∠B=∠ACE B.∠A=∠ECD C.∠B=∠ACB D.∠A=∠ACE3、如图⑨,下列推理正确的是( )A.∵∠1=∠3,∴∥ B.∵∠1=∠2,∴∥ C.∵∠1=∠2,∴ ∥ D.∵∠1=∠5,∴∥4、已知,如图∠1+∠2=180°,填空。 ∵∠1+∠2=180°( )又∵∠2=∠3( )∴∠1+∠3=180°∴_________( )5、如图,在四边形ABCD中,已知∠B=60°,∠C=120°,AB与CD平行吗? AD与BC平行吗? ( http: / / www.21cnjy.com ) 独立完成. (2分钟)先试着自己完成,有问题的小组交流,小组展示(5分钟)独立完成后,小组讨论,共同订正(5分钟)先试着自己完成,有问题的小组交流,小组展示(6分钟)认真读题,首先自己仔细分析,解决问题,然后与对子交流对照。(5分钟)自己总结(1分钟)要求先独立思考,自主完成,再与对子交流互查(4分钟) 学生独立完成,给学生发言的机会。注意规范学生过程的书写。
几何语言:
∵______________
∴_____________.
70°
70°
70°
C
D
E
B
A
F
几何语言:
∵________________
∴_______________.
A
1
2
B
C
D
F
E
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
