2023-2024学年初中数学北师版七年级下册第二章 相交线与平行线 单元练习(含答案)
文档属性
| 名称 | 2023-2024学年初中数学北师版七年级下册第二章 相交线与平行线 单元练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 218.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 06:41:02 | ||
图片预览


文档简介
第二章 相交线与平行线
(时间:120分钟 满分:120分)
题号 一 二 三 四 五 六 总分 累分人
得分
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
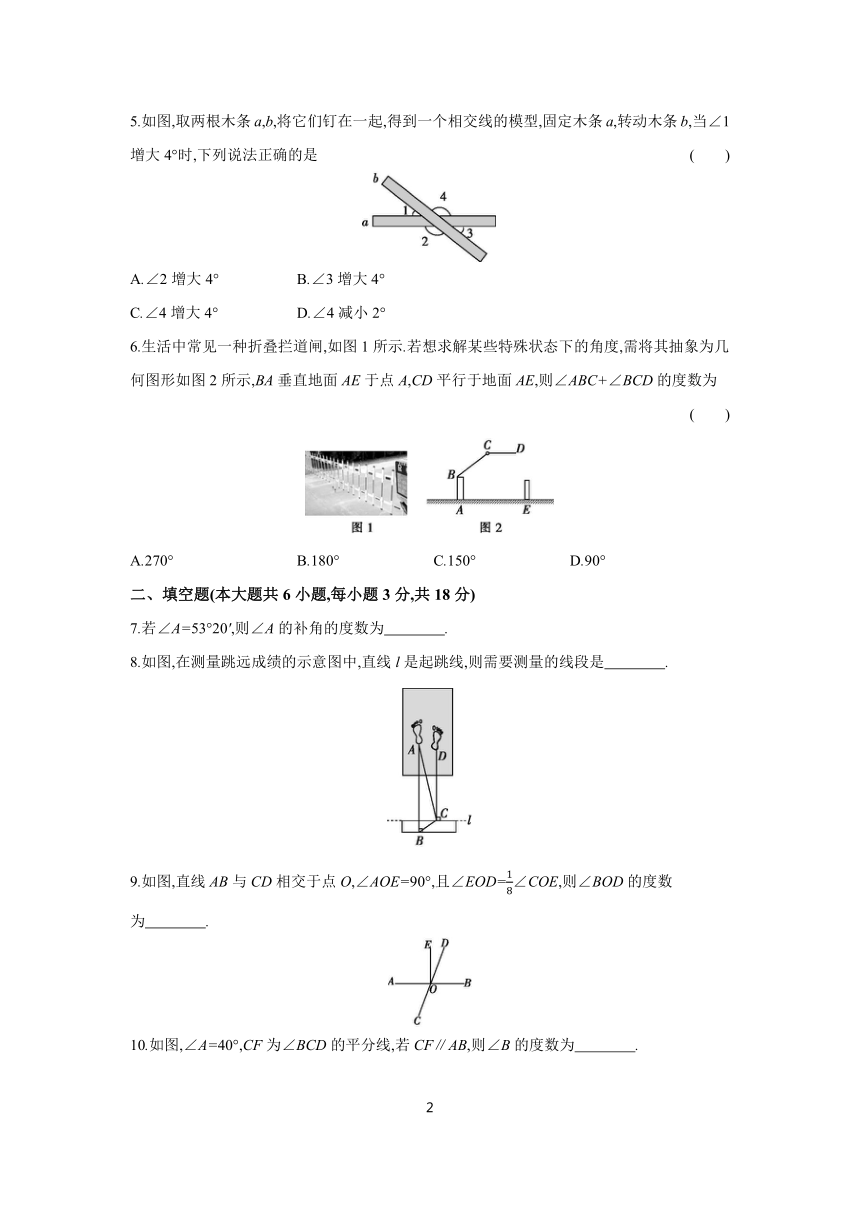
1.如图,∠BAC和∠BED是 ( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
2.如图,已知∠CBD=90°,若∠ABC=36°,AB∥EF,则∠DFE的度数是 ( )
A.36° B.64° C.54° D.63°
3.如图,AB⊥l,BC⊥l,B为垂足,下列说法正确的是 ( )
A.点A到l的距离是线段AB
B.点C到点A的距离是线段AC
C.A、C、B三点共线
D.A、C、B三点不一定共线
4.如图,用尺规作出∠NCB=∠AOC,则作图痕迹中,弧FG是 ( )
A.以点C为圆心,OD为半径的弧 B.以点C为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧 D.以点E为圆心,DM为半径的弧
5.如图,取两根木条a,b,将它们钉在一起,得到一个相交线的模型,固定木条a,转动木条b,当∠1增大4°时,下列说法正确的是 ( )
A.∠2增大4° B.∠3增大4°
C.∠4增大4° D.∠4减小2°
6.生活中常见一种折叠拦道闸,如图1所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形如图2所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD的度数为 ( )
A.270° B.180° C.150° D.90°
二、填空题(本大题共6小题,每小题3分,共18分)
7.若∠A=53°20',则∠A的补角的度数为 .
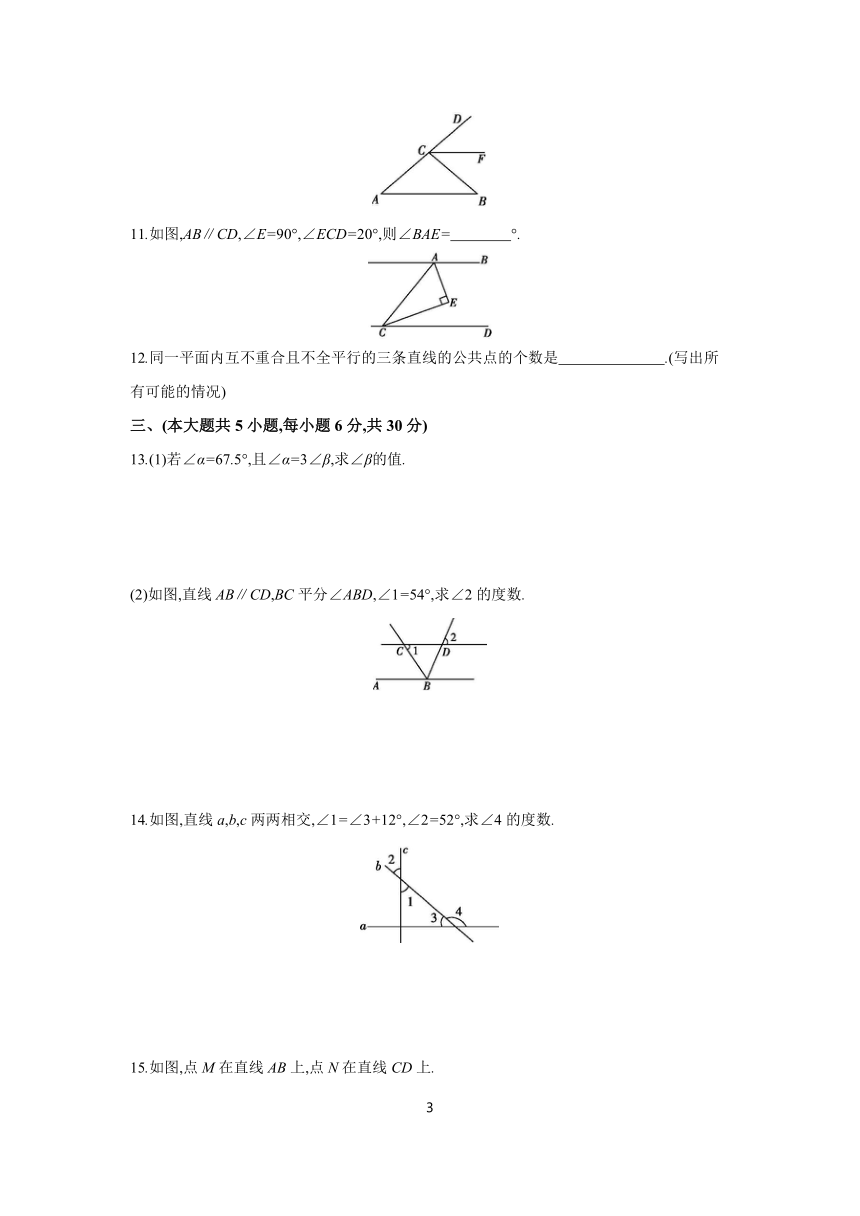
8.如图,在测量跳远成绩的示意图中,直线l是起跳线,则需要测量的线段是 .
9.如图,直线AB与CD相交于点O,∠AOE=90°,且∠EOD=∠COE,则∠BOD的度数为 .
10.如图,∠A=40°,CF为∠BCD的平分线,若CF∥AB,则∠B的度数为 .
11.如图,AB∥CD,∠E=90°,∠ECD=20°,则∠BAE= °.
12.同一平面内互不重合且不全平行的三条直线的公共点的个数是 .(写出所有可能的情况)
三、(本大题共5小题,每小题6分,共30分)
13.(1)若∠α=67.5°,且∠α=3∠β,求∠β的值.
(2)如图,直线AB∥CD,BC平分∠ABD,∠1=54°,求∠2的度数.
14.如图,直线a,b,c两两相交,∠1=∠3+12°,∠2=52°,求∠4的度数.
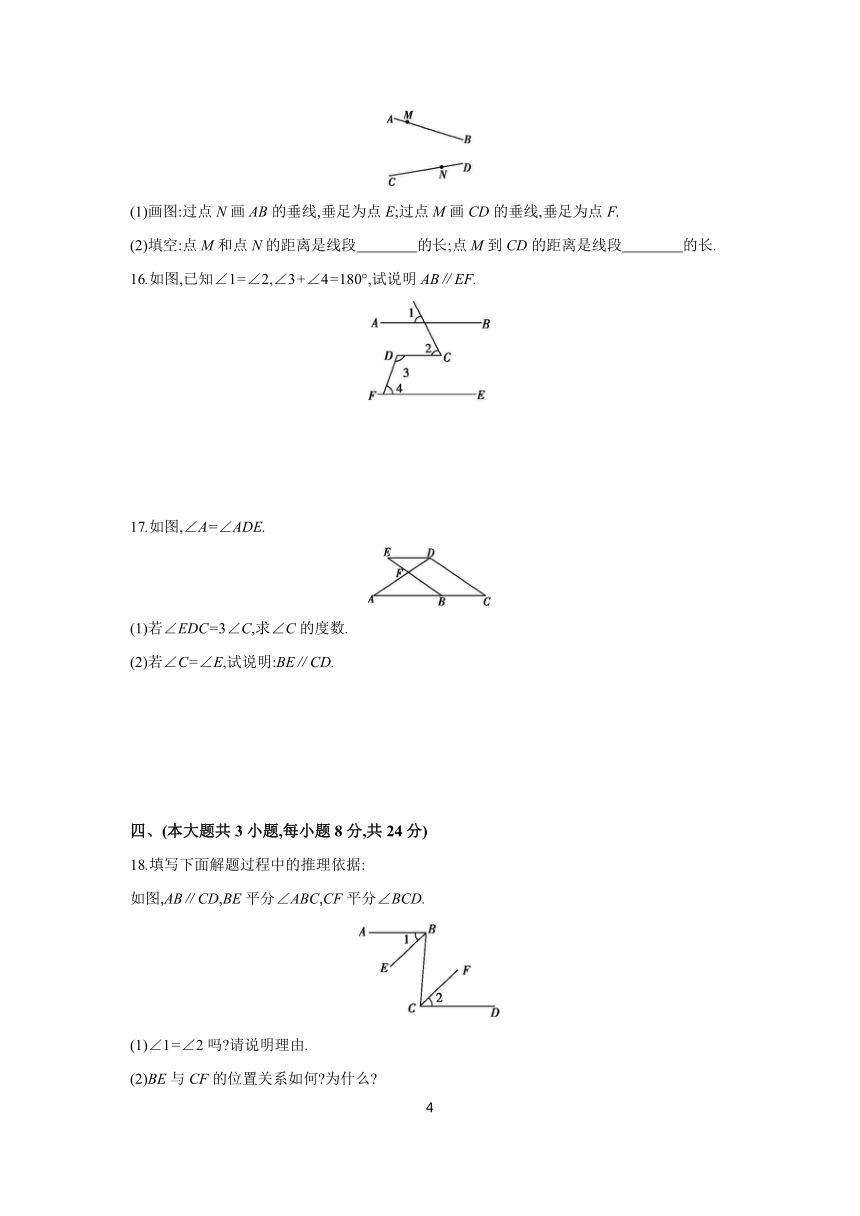
15.如图,点M在直线AB上,点N在直线CD上.
(1)画图:过点N画AB的垂线,垂足为点E;过点M画CD的垂线,垂足为点F.
(2)填空:点M和点N的距离是线段 的长;点M到CD的距离是线段 的长.
16.如图,已知∠1=∠2,∠3+∠4=180°,试说明AB∥EF.
17.如图,∠A=∠ADE.
(1)若∠EDC=3∠C,求∠C的度数.
(2)若∠C=∠E,试说明:BE∥CD.
四、(本大题共3小题,每小题8分,共24分)
18.填写下面解题过程中的推理依据:
如图,AB∥CD,BE平分∠ABC,CF平分∠BCD.
(1)∠1=∠2吗 请说明理由.
(2)BE与CF的位置关系如何 为什么
(本题第(1)小题在下面的解答过程的空格内填写理由或数学式,第(2)小题要写出解题过程)
解:(1)∠1=∠2,理由如下:
因为AB∥CD(已知),
所以∠ABC=∠BCD( ).
因为BE平分∠ABC,CF平分∠BCD(已知),
所以∠1=∠ (角平分线的定义),∠2=∠ (角平分线的定义),
所以∠1=∠2( ).
(2)
19.如图,直线AB,CD相交于点O,已知∠BOC=75°,ON将∠AOD分成两个角,且∠AON∶∠NOD=2∶3.
(1)求∠AON的度数.
(2)若OM平分∠BON,则OB是∠COM的平分线吗 判断并说明理由.
20.如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.
(1)试说明∠1=∠2.
(2)已知∠2=54°,求∠BEF的度数.
五、(本大题共2小题,每小题9分,共18分)
21.“村村通”是国家的一个系统工程,其中包含公路、电力、生活饮用水、电话网、有线电视网、互联网等等.如图,现计划在A村,B村,C村周边修公路,公路从A村沿北偏东65°方向到B村,对B村沿北偏西25°方向到C村,那么要想在C村修公路CE,CE与CB有点怎样的位置关系,可以保证CE与AB平行
22.如图1,以直线AB上一点O为顶点作射线OC,使∠BOC=75°.将一个直角三角板DOE的直角顶点O放在直线AB上的点O处,边OD放在射线OB上.
(1)∠COE= .
(2)如图2,将直角三角板DOE绕点O按逆时针方向转动,当射线OC恰好平分∠BOE时,求∠COD的度数.
(3)如图3,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系,并说明理由.
六、(本大题共12分)
23.如图,已知直线l1∥l2,直线l和直线l1、l2分别交于点C、D,点A,B在直线l的同侧,在直线l上有一点P.
(1)当点P在C,D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化 为什么
(2)当点P在C,D两点的外侧运动时(点P与点C,D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何 请说明理由.
参考答案
1.A 2.C 3.C 4.D 5.B 6.A
7.126°40' 8.CD 9.70° 10.40° 11.70
12.1或2或3 提示:如图,有以下三种情况,
13.(1)解:因为∠α=67.5°,∠α=3∠β.
解得∠β=22.5°=22°30'. 3分
(2)解:如图,因为直线AB∥CD,
所以∠1=∠3=54°. 1分
因为BC平分∠ABD,
所以∠3=∠4=54°, 2分
所以∠2=180°-54°-54°=72°. 3分
14.解:因为∠1与∠2是对顶角,
所以∠1=∠2=52°. 2分
因为∠1=∠3+12°=52°,
所以∠3=40°. 4分
因为∠3与∠4是邻补角,
所以∠4=180°-∠3=180°-40°=140°. 6分
15.解:(1)如图所示. 4分
(2)MN;MF. 6分
16.解:因为∠1=∠2,
所以AB∥CD. 2分
因为∠3+∠4=180°,
所以CD∥EF,
所以AB∥EF. 6分
17.解:(1)因为∠A=∠ADE,
所以AC∥DE,
所以∠EDC+∠C=180°.
又因为∠EDC=3∠C,
所以4∠C=180°,
所以∠C=45°. 3分
(2)因为∠A=∠ADE,
所以AC∥DE,
所以∠E=∠ABE.
又因为∠C=∠E,
所以∠C=∠ABE,
所以BE∥CD. 6分
18.解:(1)两直线平行,内错角相等;ABC;BCD;等量代换. 4分
(2)BE∥CF,理由如下:
由(1)可知∠ABC=∠BCD.
因为BE平分∠ABC,CF平分∠BCD(已知),
所以∠EBC=∠ABC(角平分线的定义),∠FCB=∠BCD(角平分线的定义),
所以∠ECB=∠FCB(等量代换),
所以BE∥CF(内错角相等,两直线平行). 8分
19.解:(1)因为∠AON∶∠NOD=2∶3,
设∠AON=2x,∠NOD=3x,
所以∠AOD=5x.
因为∠BOC=75°,
所以∠AOD=5x=75°,
所以x=15°,
所以∠AON=30°. 3分
(2)OB是∠COM的平分线. 4分
理由:因为∠AON=30°,
所以∠BON=180°-∠AON=150°.
因为OM平分∠BON,
所以∠BOM=75°,
所以∠BOM=∠BOC,
所以OB是∠COM的平分线. 8分
20.解:(1)因为AB∥CD,
所以∠MEB=∠MFD.
因为A'E∥C'F,
所以∠MEA'=∠MFC',
所以∠MEA'-∠MEB=∠MFC'-∠MFD,
即∠1=∠2. 4分
(2)由折叠知,∠C'FN==63°.
因为A'E∥C'F,
所以∠A'EN=∠C'FN=63°.
因为∠1=∠2=54°,
所以∠BEF=63°+54°=117°. 8分
21.解:CE⊥CB. 2分
理由如下:如图,由题意得AD∥BF,
所以∠ABF=180°-65°=115°,
所以∠ABC=115°-25°=90°, 5分
要使CE∥AB,
则∠ECB=∠ABC=90°, 7分
所以CE⊥CB. 9分
22.解(1)15°. 2分
(2)因为OC平分∠BOE,∠BOC=75°,
所以∠EOC=∠BOC=75°.
因为∠DOE=90°,
所以∠COD=∠DOE-∠EOC=90°-75°=15°. 6分
(3)∠COE-∠BOD=15°. 7分
理由:因为∠COE=90°-∠COD,∠BOD=75°-∠COD,
所以∠COE-∠BOD=(90°-∠COD)-(75°-∠COD)=15°. 9分
23.解:(1)不会发生变化.原因略. 4分
(2)若点P在C、D两点的外侧运动时(点P与点C、D不重合),则有两种情形:
①如图1,有结论:∠APB=∠PBD-∠PAC.理由如下:过点P作PE∥l1,则∠APE=∠PAC,又因为l1∥l2,所以PE∥l2,所以∠BPE=∠PBD,所以∠APB=∠BPE-∠APE=∠PBD-∠PAC,即∠APB=∠PBD-∠PAC; 8分
②如图2,有结论:∠APB=∠PAC-∠PBD.理由如下:过点P作PE∥l2,则∠BPE=∠PBD,又因为l1∥l2,所以PE∥l1,所以∠APE=∠PAC,所以∠APB=∠APE-∠BPE=∠PAC-∠PBD,即∠APB=∠PAC-∠PBD. 12分
2
(时间:120分钟 满分:120分)
题号 一 二 三 四 五 六 总分 累分人
得分
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
1.如图,∠BAC和∠BED是 ( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
2.如图,已知∠CBD=90°,若∠ABC=36°,AB∥EF,则∠DFE的度数是 ( )
A.36° B.64° C.54° D.63°
3.如图,AB⊥l,BC⊥l,B为垂足,下列说法正确的是 ( )
A.点A到l的距离是线段AB
B.点C到点A的距离是线段AC
C.A、C、B三点共线
D.A、C、B三点不一定共线
4.如图,用尺规作出∠NCB=∠AOC,则作图痕迹中,弧FG是 ( )
A.以点C为圆心,OD为半径的弧 B.以点C为圆心,DM为半径的弧
C.以点E为圆心,OD为半径的弧 D.以点E为圆心,DM为半径的弧
5.如图,取两根木条a,b,将它们钉在一起,得到一个相交线的模型,固定木条a,转动木条b,当∠1增大4°时,下列说法正确的是 ( )
A.∠2增大4° B.∠3增大4°
C.∠4增大4° D.∠4减小2°
6.生活中常见一种折叠拦道闸,如图1所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形如图2所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD的度数为 ( )
A.270° B.180° C.150° D.90°
二、填空题(本大题共6小题,每小题3分,共18分)
7.若∠A=53°20',则∠A的补角的度数为 .
8.如图,在测量跳远成绩的示意图中,直线l是起跳线,则需要测量的线段是 .
9.如图,直线AB与CD相交于点O,∠AOE=90°,且∠EOD=∠COE,则∠BOD的度数为 .
10.如图,∠A=40°,CF为∠BCD的平分线,若CF∥AB,则∠B的度数为 .
11.如图,AB∥CD,∠E=90°,∠ECD=20°,则∠BAE= °.
12.同一平面内互不重合且不全平行的三条直线的公共点的个数是 .(写出所有可能的情况)
三、(本大题共5小题,每小题6分,共30分)
13.(1)若∠α=67.5°,且∠α=3∠β,求∠β的值.
(2)如图,直线AB∥CD,BC平分∠ABD,∠1=54°,求∠2的度数.
14.如图,直线a,b,c两两相交,∠1=∠3+12°,∠2=52°,求∠4的度数.
15.如图,点M在直线AB上,点N在直线CD上.
(1)画图:过点N画AB的垂线,垂足为点E;过点M画CD的垂线,垂足为点F.
(2)填空:点M和点N的距离是线段 的长;点M到CD的距离是线段 的长.
16.如图,已知∠1=∠2,∠3+∠4=180°,试说明AB∥EF.
17.如图,∠A=∠ADE.
(1)若∠EDC=3∠C,求∠C的度数.
(2)若∠C=∠E,试说明:BE∥CD.
四、(本大题共3小题,每小题8分,共24分)
18.填写下面解题过程中的推理依据:
如图,AB∥CD,BE平分∠ABC,CF平分∠BCD.
(1)∠1=∠2吗 请说明理由.
(2)BE与CF的位置关系如何 为什么
(本题第(1)小题在下面的解答过程的空格内填写理由或数学式,第(2)小题要写出解题过程)
解:(1)∠1=∠2,理由如下:
因为AB∥CD(已知),
所以∠ABC=∠BCD( ).
因为BE平分∠ABC,CF平分∠BCD(已知),
所以∠1=∠ (角平分线的定义),∠2=∠ (角平分线的定义),
所以∠1=∠2( ).
(2)
19.如图,直线AB,CD相交于点O,已知∠BOC=75°,ON将∠AOD分成两个角,且∠AON∶∠NOD=2∶3.
(1)求∠AON的度数.
(2)若OM平分∠BON,则OB是∠COM的平分线吗 判断并说明理由.
20.如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.
(1)试说明∠1=∠2.
(2)已知∠2=54°,求∠BEF的度数.
五、(本大题共2小题,每小题9分,共18分)
21.“村村通”是国家的一个系统工程,其中包含公路、电力、生活饮用水、电话网、有线电视网、互联网等等.如图,现计划在A村,B村,C村周边修公路,公路从A村沿北偏东65°方向到B村,对B村沿北偏西25°方向到C村,那么要想在C村修公路CE,CE与CB有点怎样的位置关系,可以保证CE与AB平行
22.如图1,以直线AB上一点O为顶点作射线OC,使∠BOC=75°.将一个直角三角板DOE的直角顶点O放在直线AB上的点O处,边OD放在射线OB上.
(1)∠COE= .
(2)如图2,将直角三角板DOE绕点O按逆时针方向转动,当射线OC恰好平分∠BOE时,求∠COD的度数.
(3)如图3,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系,并说明理由.
六、(本大题共12分)
23.如图,已知直线l1∥l2,直线l和直线l1、l2分别交于点C、D,点A,B在直线l的同侧,在直线l上有一点P.
(1)当点P在C,D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化 为什么
(2)当点P在C,D两点的外侧运动时(点P与点C,D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何 请说明理由.
参考答案
1.A 2.C 3.C 4.D 5.B 6.A
7.126°40' 8.CD 9.70° 10.40° 11.70
12.1或2或3 提示:如图,有以下三种情况,
13.(1)解:因为∠α=67.5°,∠α=3∠β.
解得∠β=22.5°=22°30'. 3分
(2)解:如图,因为直线AB∥CD,
所以∠1=∠3=54°. 1分
因为BC平分∠ABD,
所以∠3=∠4=54°, 2分
所以∠2=180°-54°-54°=72°. 3分
14.解:因为∠1与∠2是对顶角,
所以∠1=∠2=52°. 2分
因为∠1=∠3+12°=52°,
所以∠3=40°. 4分
因为∠3与∠4是邻补角,
所以∠4=180°-∠3=180°-40°=140°. 6分
15.解:(1)如图所示. 4分
(2)MN;MF. 6分
16.解:因为∠1=∠2,
所以AB∥CD. 2分
因为∠3+∠4=180°,
所以CD∥EF,
所以AB∥EF. 6分
17.解:(1)因为∠A=∠ADE,
所以AC∥DE,
所以∠EDC+∠C=180°.
又因为∠EDC=3∠C,
所以4∠C=180°,
所以∠C=45°. 3分
(2)因为∠A=∠ADE,
所以AC∥DE,
所以∠E=∠ABE.
又因为∠C=∠E,
所以∠C=∠ABE,
所以BE∥CD. 6分
18.解:(1)两直线平行,内错角相等;ABC;BCD;等量代换. 4分
(2)BE∥CF,理由如下:
由(1)可知∠ABC=∠BCD.
因为BE平分∠ABC,CF平分∠BCD(已知),
所以∠EBC=∠ABC(角平分线的定义),∠FCB=∠BCD(角平分线的定义),
所以∠ECB=∠FCB(等量代换),
所以BE∥CF(内错角相等,两直线平行). 8分
19.解:(1)因为∠AON∶∠NOD=2∶3,
设∠AON=2x,∠NOD=3x,
所以∠AOD=5x.
因为∠BOC=75°,
所以∠AOD=5x=75°,
所以x=15°,
所以∠AON=30°. 3分
(2)OB是∠COM的平分线. 4分
理由:因为∠AON=30°,
所以∠BON=180°-∠AON=150°.
因为OM平分∠BON,
所以∠BOM=75°,
所以∠BOM=∠BOC,
所以OB是∠COM的平分线. 8分
20.解:(1)因为AB∥CD,
所以∠MEB=∠MFD.
因为A'E∥C'F,
所以∠MEA'=∠MFC',
所以∠MEA'-∠MEB=∠MFC'-∠MFD,
即∠1=∠2. 4分
(2)由折叠知,∠C'FN==63°.
因为A'E∥C'F,
所以∠A'EN=∠C'FN=63°.
因为∠1=∠2=54°,
所以∠BEF=63°+54°=117°. 8分
21.解:CE⊥CB. 2分
理由如下:如图,由题意得AD∥BF,
所以∠ABF=180°-65°=115°,
所以∠ABC=115°-25°=90°, 5分
要使CE∥AB,
则∠ECB=∠ABC=90°, 7分
所以CE⊥CB. 9分
22.解(1)15°. 2分
(2)因为OC平分∠BOE,∠BOC=75°,
所以∠EOC=∠BOC=75°.
因为∠DOE=90°,
所以∠COD=∠DOE-∠EOC=90°-75°=15°. 6分
(3)∠COE-∠BOD=15°. 7分
理由:因为∠COE=90°-∠COD,∠BOD=75°-∠COD,
所以∠COE-∠BOD=(90°-∠COD)-(75°-∠COD)=15°. 9分
23.解:(1)不会发生变化.原因略. 4分
(2)若点P在C、D两点的外侧运动时(点P与点C、D不重合),则有两种情形:
①如图1,有结论:∠APB=∠PBD-∠PAC.理由如下:过点P作PE∥l1,则∠APE=∠PAC,又因为l1∥l2,所以PE∥l2,所以∠BPE=∠PBD,所以∠APB=∠BPE-∠APE=∠PBD-∠PAC,即∠APB=∠PBD-∠PAC; 8分
②如图2,有结论:∠APB=∠PAC-∠PBD.理由如下:过点P作PE∥l2,则∠BPE=∠PBD,又因为l1∥l2,所以PE∥l1,所以∠APE=∠PAC,所以∠APB=∠APE-∠BPE=∠PAC-∠PBD,即∠APB=∠PAC-∠PBD. 12分
2
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
