2023-2024学年初中数学北师版七年级下册第四章 三角形 单元练习(含答案)
文档属性
| 名称 | 2023-2024学年初中数学北师版七年级下册第四章 三角形 单元练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 206.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 00:00:00 | ||
图片预览


文档简介
第四章 三角形数学
(时间:120分钟 满分:120分)
题号 一 二 三 四 五 六 总分 累分人
得分
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
1.下列各组图形中,属于全等图形的是 ( )
2.下列长度的三条线段不能组成三角形的是 ( )
A.3 cm、4 cm、5 cm B.4 cm、5 cm、6 cm
C.2 cm、4 cm、7 cm D.5 cm、12 cm、13 cm
3.下列图形中,△ABC的高画法错误的是 ( )
4.如图,AB=DE,∠B=∠DEF,添加下列其中一个条件后,仍无法证明△ABC≌△DEF的是 ( )
A.AC=DF
B.BE=CF
C.∠A=∠D
D.AC∥DF
5.如图,小亮要测量水池AB的宽度,但没有足够长的绳子,聪明的他设计了一个方案.请将方案补充完整,并说明方案成立的理由.其中错误的是 ( )
(1)先在地上取一个可以直接到达A点和B点的点C.
(2)连接BC并延长到点E,使得△.
(3)连接AC并延长到点D,使得▽.
(4)连接〇并测量出它的长度,就是AB的长.
(5)上述方案的依据是◇.
A.△代表CE=BC B.▽代表CD=CA
C.〇代表DE D.◇代表SSS
6.如图,△ABC≌△ADE,点A、B、D在同一条直线上,BC分别与AE、DE交于点F、H,DE与AC交于点G.有下列三个结论:(1)∠BAF=∠DAG;(2)△ABF≌△ADG;(3)HF=HG.其中正确结论的个数是 ( )
A.1 B.2
C.3 D.无法判断
二、填空题(本大题共6小题,每小题3分,共18分)
7.如图,这是一块三角形木板的残余部分,量得∠A=106°,∠B=34°,则这块三角形木板缺少的角的度数是 .
8.如图,自行车的车架上常常会焊接一条横梁,运用的数学原理是 .
9.如图,在△ABC中,已知AB=8 cm,AC=5 cm,AD是△ABC的中线,则△ABD的周长比△ACD的周长多 cm.
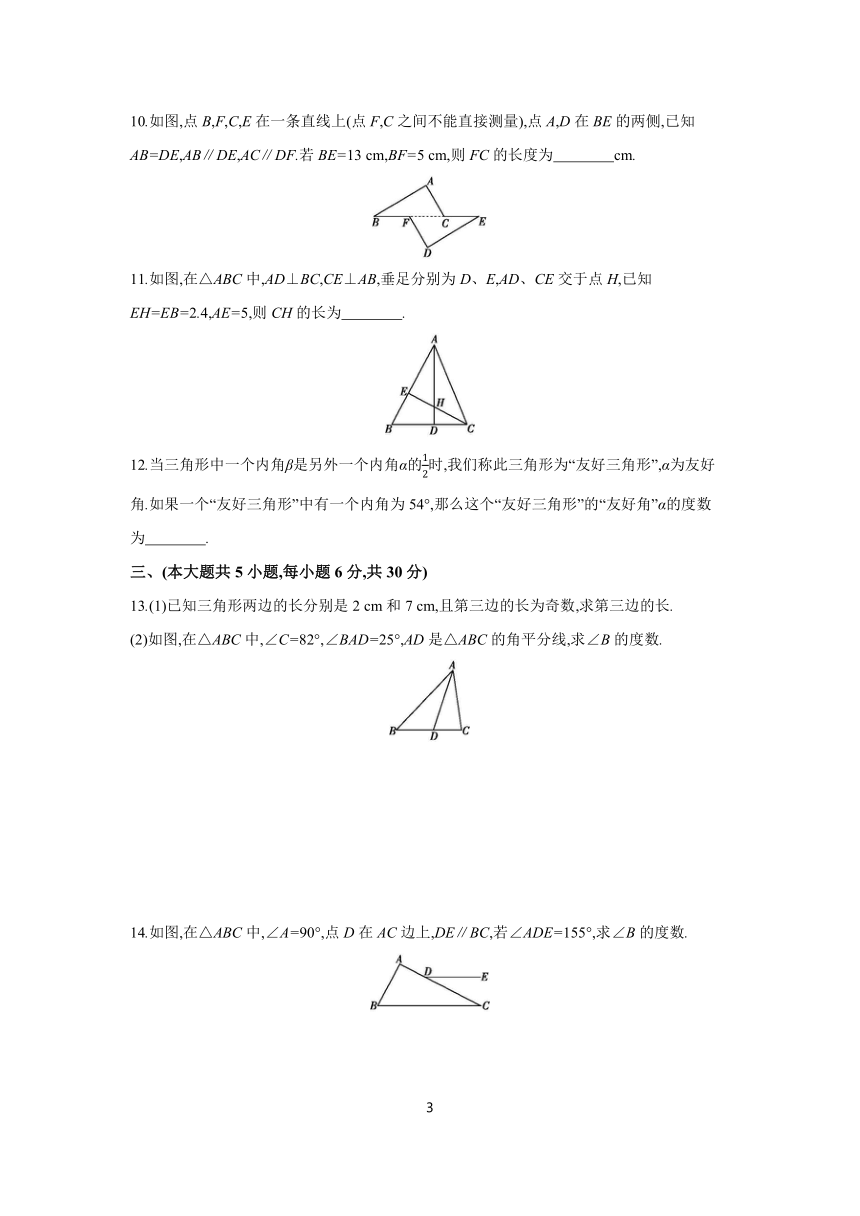
10.如图,点B,F,C,E在一条直线上(点F,C之间不能直接测量),点A,D在BE的两侧,已知AB=DE,AB∥DE,AC∥DF.若BE=13 cm,BF=5 cm,则FC的长度为 cm.
11.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=2.4,AE=5,则CH的长为 .
12.当三角形中一个内角β是另外一个内角α的时,我们称此三角形为“友好三角形”,α为友好角.如果一个“友好三角形”中有一个内角为54°,那么这个“友好三角形”的“友好角”α的度数为 .
三、(本大题共5小题,每小题6分,共30分)
13.(1)已知三角形两边的长分别是2 cm和7 cm,且第三边的长为奇数,求第三边的长.
(2)如图,在△ABC中,∠C=82°,∠BAD=25°,AD是△ABC的角平分线,求∠B的度数.
14.如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠ADE=155°,求∠B的度数.
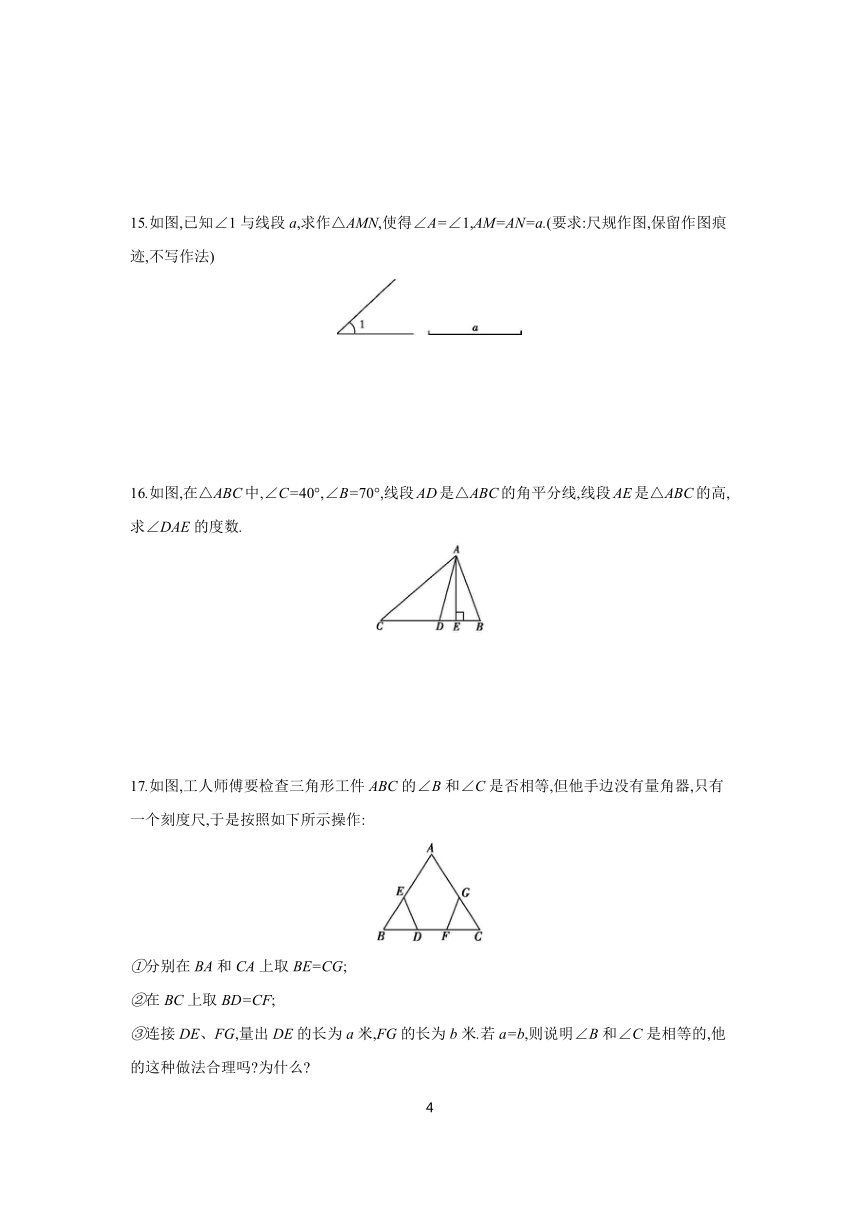
15.如图,已知∠1与线段a,求作△AMN,使得∠A=∠1,AM=AN=a.(要求:尺规作图,保留作图痕迹,不写作法)
16.如图,在△ABC中,∠C=40°,∠B=70°,线段AD是△ABC的角平分线,线段AE是△ABC的高,求∠DAE的度数.
17.如图,工人师傅要检查三角形工件ABC的∠B和∠C是否相等,但他手边没有量角器,只有一个刻度尺,于是按照如下所示操作:
①分别在BA和CA上取BE=CG;
②在BC上取BD=CF;
③连接DE、FG,量出DE的长为a米,FG的长为b米.若a=b,则说明∠B和∠C是相等的,他的这种做法合理吗 为什么
四、(本大题共3小题,每小题8分,共24分)
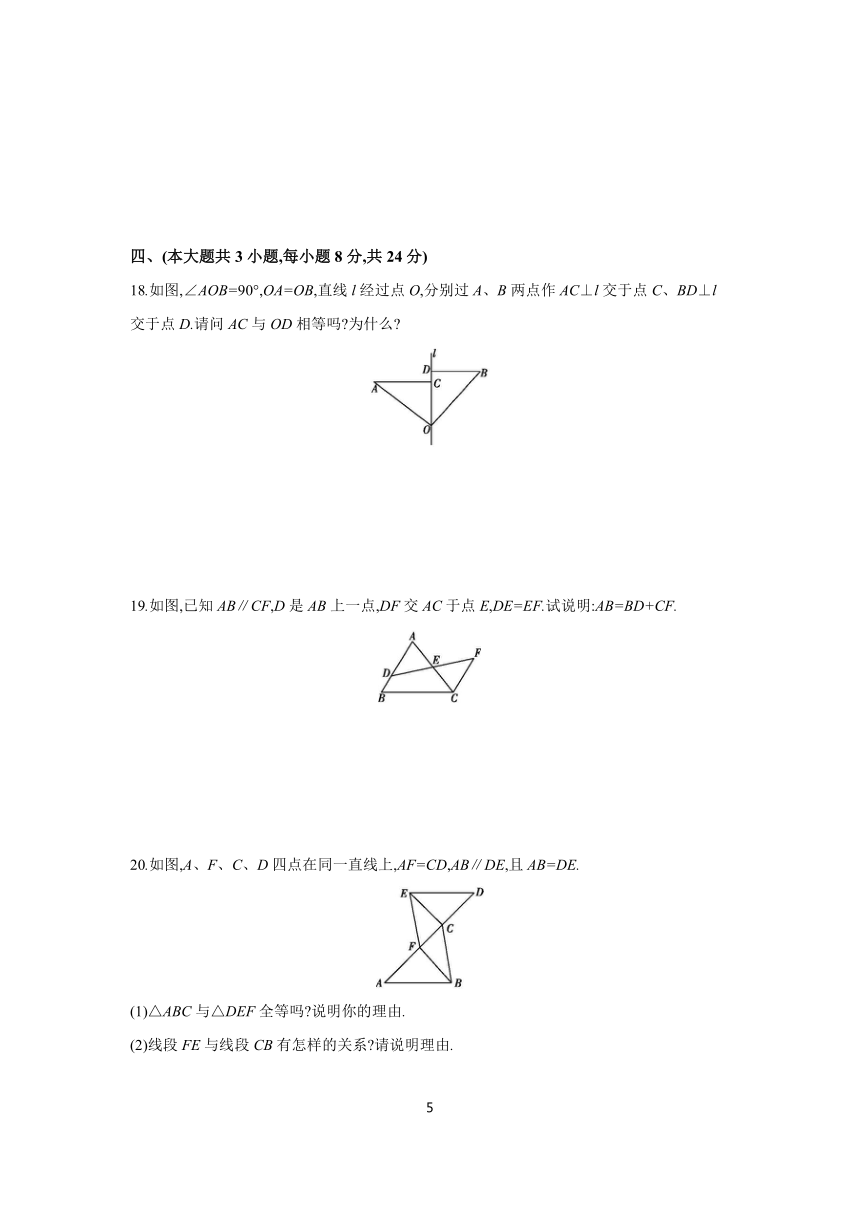
18.如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A、B两点作AC⊥l交于点C、BD⊥l交于点D.请问AC与OD相等吗 为什么
19.如图,已知AB∥CF,D是AB上一点,DF交AC于点E,DE=EF.试说明:AB=BD+CF.
20.如图,A、F、C、D四点在同一直线上,AF=CD,AB∥DE,且AB=DE.
(1)△ABC与△DEF全等吗 说明你的理由.
(2)线段FE与线段CB有怎样的关系 请说明理由.
五、(本大题共2小题,每小题9分,共18分)
21.【概念认识】
如图1,在∠ABC中,若∠ABD=∠DBE=∠EBC,则BD,BE叫做∠ABC的“三分线”,其中BD是“邻BA三分线”,BE是“邻BC三分线”.
【问题解决】
(1)如图2,在△ABC中,∠A=70°,∠ABC=45°,若∠ABC的“邻BA三分线”BD交AC于点D,则∠BDC的度数为 .
(2)如图3,在△ABC中,BP,CP分别是∠ABC“邻BA三分线”和∠ACB“邻CA三分线”,且BP⊥PC,求∠A的度数.
22.如图,在△ABC中,AD是BC边上的中线,交BC于点D.
(1)如图1,延长AD到点E,使DE=AD,连接BE.求证:△ACD≌△EBD.
(2)如图2,若∠BAC=90°,试探究AD与BC有何数量关系,并说明理由.
六、(本大题共12分)
23.在△ABC中,AB=AC,∠B=∠C,D、E、F分别是边BC、AB、AC的中点,沿DE将△BDE折叠得到△GDE,点B的对应点为点G,沿DF将△CDF折叠得到△HDF,点C的对应点为点H,连接AG、AH.
(1)当点G、H与点A重合时,DE与AB的位置关系是 .
(2)如图,当点G、H不与点A重合时.
①△BDE与△CDF全等吗 请说明理由.
②AG与AH相等吗 请说明理由.
参考答案
1.B 2.C 3.B 4.A 5.D 6.C
7.40° 8.三角形具有稳定性 9.67.5° 10.3 11.2.6
12.54°或84°或108° 提示:①若54°角是α,则友好角度数为54°;②若54°角是β,则α=β=54°,所以“友好角”α=108°;③若54°角既不是α也不是β,则α+β+54°=180°,所以α+α+54°=180°,解得α=84°.综上所述,“友好角”度数为54°或84°或108°.故答案为54°或84°或108°.
13.(1)解:设此三角形的第三边长为x cm,则5因为第三边的长为奇数,
所以x=7,
即第三边的长为7 cm. 3分
(2)解:因为∠BAD=25°,AD是△ABC的角平分线,
所以∠BAC=2∠BAD=50°.
因为∠C=82°,
所以∠B=180°-∠C-∠BAC=48°. 3分
14.解:因为∠ADE=155°,∠ADE+∠CDE=180°,
所以∠CDE=25°. 2分
因为DE∥BC,
所以∠C=∠CDE=25°. 4分
在△ABC中,∠A=90°,
所以∠B=90°-25°=65°. 6分
15.解:如图,△AMN即为所求. 6分
16.解:因为∠B=70°,∠C=40°,所以∠BAC=70°.
因为AD是△ABC的角平分线,所以∠DAB=35°,
所以∠ADE=180°-∠DAB-∠B=75°.
因为AE是△ABC的高,所以∠AED=90°,
所以∠DAE=90°-∠ADE=15°. 6分
17.解:这种做法合理. 1分
理由如下:
在△BDE和△CFG中,
所以△BDE≌△CFG(SSS),
所以∠B=∠C. 6分
18.解:AC=OD. 1分
因为∠AOB=90°,
所以∠AOC+∠BOD=90°.
因为AC⊥l,BD⊥l,
所以∠ACO=∠BDO=90°,
所以∠A+∠AOC=90°,
所以∠A=∠BOD. 4分
又因为OA=OB,
所以△AOC≌△OBD,
所以AC=OD. 8分
19.解:因为AB∥CF,
所以∠A=∠ACF,∠ADF=∠F. 2分
在△ADE和△CFE中,
所以△ADE≌△CFE(AAS), 6分
所以AD=CF. 7分
因为AB=BD+AD,
所以AB=BD+CF. 8分
20.解:(1)△ABC≌△DEF. 1分
理由:因为AF=CD,所以AF+FC=CD+FC,即AC=DF. 2分
因为AB∥DE,所以∠D=∠A. 3分
在△ABC和△DEF中,
所以△ABC≌△DEF. 5分
(2)平行且相等. 6分
理由:因为△ABC≌△DEF,所以∠EFC=∠FCB,EF=CB, 7分
所以FE∥CB. 8分
21.解:(1)85°. 3分
(2)因为BP⊥PC,
所以∠BPC=90°,
所以∠PBC+∠PCB=90°. 6分
因为BP,CP分别是∠ABC“邻BA三分线”和“∠ACB邻CA三分线”,
所以∠ABC+∠ACB=90°,
所以∠ABC+∠ACB=135°,
所以∠A=180°-(∠ABC+∠ACB)=45°. 9分
22.解:(1)证明:因为AD是BC边上的中线,
所以CD=BD.
在△ACD和△EBD中,
所以△ACD≌△EBD(SAS). 3分
(2)AD与BC的数量关系为AD=BC. 4分
理由如下:延长AD到点E,使DE=AD,连接BE,如图所示.
同(1)得△ACD≌△EBD(SAS),
所以AC=BE,∠DAC=∠DEB,
所以AC∥BE,
所以∠BAC+∠ABE=180°.
因为∠BAC=90°,
所以∠BAC=∠ABE=90°. 6分
在△BAC和△ABE中,
所以△BAC≌△ABE(SAS),
所以BC=AE.
因为AD=DE=AE,
所以AD=BC. 9分
23.解:(1)DE⊥AB. 2分
(2)①△BDE≌△CDF. 3分
理由:因为D是边BC的中点,
所以BD=CD.
因为E、F分别是边AB、AC的中点,
所以BE=AB,CF=AC.
又因为AB=AC,
所以BE=CF. 5分
在△BDE和△CDF中,
所以△BDE≌△CDF(SAS). 7分
②AG=AH. 8分
理由:因为∠AEG=∠BED+∠DEG-180°,
所以∠AEG=2∠BED-180°.
因为∠AFH=∠CFD+∠DFH-180°,
所以∠AFH=2∠CFD-180°.
因为△BDE≌△CDF,
所以∠BED=∠CFD,
所以∠AEG=∠AFH. 9分
因为AE=BE=GE=AB,AF=CF=HF=AC,AB=AC,
所以AE=AF,GE=HF. 10分
在△AEG和△AFH中,
所以△AEG≌△AFH(SAS),
所以AG=AH. 12分
(用其他方法说明理由,亦相应给分)
2
(时间:120分钟 满分:120分)
题号 一 二 三 四 五 六 总分 累分人
得分
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
1.下列各组图形中,属于全等图形的是 ( )
2.下列长度的三条线段不能组成三角形的是 ( )
A.3 cm、4 cm、5 cm B.4 cm、5 cm、6 cm
C.2 cm、4 cm、7 cm D.5 cm、12 cm、13 cm
3.下列图形中,△ABC的高画法错误的是 ( )
4.如图,AB=DE,∠B=∠DEF,添加下列其中一个条件后,仍无法证明△ABC≌△DEF的是 ( )
A.AC=DF
B.BE=CF
C.∠A=∠D
D.AC∥DF
5.如图,小亮要测量水池AB的宽度,但没有足够长的绳子,聪明的他设计了一个方案.请将方案补充完整,并说明方案成立的理由.其中错误的是 ( )
(1)先在地上取一个可以直接到达A点和B点的点C.
(2)连接BC并延长到点E,使得△.
(3)连接AC并延长到点D,使得▽.
(4)连接〇并测量出它的长度,就是AB的长.
(5)上述方案的依据是◇.
A.△代表CE=BC B.▽代表CD=CA
C.〇代表DE D.◇代表SSS
6.如图,△ABC≌△ADE,点A、B、D在同一条直线上,BC分别与AE、DE交于点F、H,DE与AC交于点G.有下列三个结论:(1)∠BAF=∠DAG;(2)△ABF≌△ADG;(3)HF=HG.其中正确结论的个数是 ( )
A.1 B.2
C.3 D.无法判断
二、填空题(本大题共6小题,每小题3分,共18分)
7.如图,这是一块三角形木板的残余部分,量得∠A=106°,∠B=34°,则这块三角形木板缺少的角的度数是 .
8.如图,自行车的车架上常常会焊接一条横梁,运用的数学原理是 .
9.如图,在△ABC中,已知AB=8 cm,AC=5 cm,AD是△ABC的中线,则△ABD的周长比△ACD的周长多 cm.
10.如图,点B,F,C,E在一条直线上(点F,C之间不能直接测量),点A,D在BE的两侧,已知AB=DE,AB∥DE,AC∥DF.若BE=13 cm,BF=5 cm,则FC的长度为 cm.
11.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=2.4,AE=5,则CH的长为 .
12.当三角形中一个内角β是另外一个内角α的时,我们称此三角形为“友好三角形”,α为友好角.如果一个“友好三角形”中有一个内角为54°,那么这个“友好三角形”的“友好角”α的度数为 .
三、(本大题共5小题,每小题6分,共30分)
13.(1)已知三角形两边的长分别是2 cm和7 cm,且第三边的长为奇数,求第三边的长.
(2)如图,在△ABC中,∠C=82°,∠BAD=25°,AD是△ABC的角平分线,求∠B的度数.
14.如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠ADE=155°,求∠B的度数.
15.如图,已知∠1与线段a,求作△AMN,使得∠A=∠1,AM=AN=a.(要求:尺规作图,保留作图痕迹,不写作法)
16.如图,在△ABC中,∠C=40°,∠B=70°,线段AD是△ABC的角平分线,线段AE是△ABC的高,求∠DAE的度数.
17.如图,工人师傅要检查三角形工件ABC的∠B和∠C是否相等,但他手边没有量角器,只有一个刻度尺,于是按照如下所示操作:
①分别在BA和CA上取BE=CG;
②在BC上取BD=CF;
③连接DE、FG,量出DE的长为a米,FG的长为b米.若a=b,则说明∠B和∠C是相等的,他的这种做法合理吗 为什么
四、(本大题共3小题,每小题8分,共24分)
18.如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A、B两点作AC⊥l交于点C、BD⊥l交于点D.请问AC与OD相等吗 为什么
19.如图,已知AB∥CF,D是AB上一点,DF交AC于点E,DE=EF.试说明:AB=BD+CF.
20.如图,A、F、C、D四点在同一直线上,AF=CD,AB∥DE,且AB=DE.
(1)△ABC与△DEF全等吗 说明你的理由.
(2)线段FE与线段CB有怎样的关系 请说明理由.
五、(本大题共2小题,每小题9分,共18分)
21.【概念认识】
如图1,在∠ABC中,若∠ABD=∠DBE=∠EBC,则BD,BE叫做∠ABC的“三分线”,其中BD是“邻BA三分线”,BE是“邻BC三分线”.
【问题解决】
(1)如图2,在△ABC中,∠A=70°,∠ABC=45°,若∠ABC的“邻BA三分线”BD交AC于点D,则∠BDC的度数为 .
(2)如图3,在△ABC中,BP,CP分别是∠ABC“邻BA三分线”和∠ACB“邻CA三分线”,且BP⊥PC,求∠A的度数.
22.如图,在△ABC中,AD是BC边上的中线,交BC于点D.
(1)如图1,延长AD到点E,使DE=AD,连接BE.求证:△ACD≌△EBD.
(2)如图2,若∠BAC=90°,试探究AD与BC有何数量关系,并说明理由.
六、(本大题共12分)
23.在△ABC中,AB=AC,∠B=∠C,D、E、F分别是边BC、AB、AC的中点,沿DE将△BDE折叠得到△GDE,点B的对应点为点G,沿DF将△CDF折叠得到△HDF,点C的对应点为点H,连接AG、AH.
(1)当点G、H与点A重合时,DE与AB的位置关系是 .
(2)如图,当点G、H不与点A重合时.
①△BDE与△CDF全等吗 请说明理由.
②AG与AH相等吗 请说明理由.
参考答案
1.B 2.C 3.B 4.A 5.D 6.C
7.40° 8.三角形具有稳定性 9.67.5° 10.3 11.2.6
12.54°或84°或108° 提示:①若54°角是α,则友好角度数为54°;②若54°角是β,则α=β=54°,所以“友好角”α=108°;③若54°角既不是α也不是β,则α+β+54°=180°,所以α+α+54°=180°,解得α=84°.综上所述,“友好角”度数为54°或84°或108°.故答案为54°或84°或108°.
13.(1)解:设此三角形的第三边长为x cm,则5
所以x=7,
即第三边的长为7 cm. 3分
(2)解:因为∠BAD=25°,AD是△ABC的角平分线,
所以∠BAC=2∠BAD=50°.
因为∠C=82°,
所以∠B=180°-∠C-∠BAC=48°. 3分
14.解:因为∠ADE=155°,∠ADE+∠CDE=180°,
所以∠CDE=25°. 2分
因为DE∥BC,
所以∠C=∠CDE=25°. 4分
在△ABC中,∠A=90°,
所以∠B=90°-25°=65°. 6分
15.解:如图,△AMN即为所求. 6分
16.解:因为∠B=70°,∠C=40°,所以∠BAC=70°.
因为AD是△ABC的角平分线,所以∠DAB=35°,
所以∠ADE=180°-∠DAB-∠B=75°.
因为AE是△ABC的高,所以∠AED=90°,
所以∠DAE=90°-∠ADE=15°. 6分
17.解:这种做法合理. 1分
理由如下:
在△BDE和△CFG中,
所以△BDE≌△CFG(SSS),
所以∠B=∠C. 6分
18.解:AC=OD. 1分
因为∠AOB=90°,
所以∠AOC+∠BOD=90°.
因为AC⊥l,BD⊥l,
所以∠ACO=∠BDO=90°,
所以∠A+∠AOC=90°,
所以∠A=∠BOD. 4分
又因为OA=OB,
所以△AOC≌△OBD,
所以AC=OD. 8分
19.解:因为AB∥CF,
所以∠A=∠ACF,∠ADF=∠F. 2分
在△ADE和△CFE中,
所以△ADE≌△CFE(AAS), 6分
所以AD=CF. 7分
因为AB=BD+AD,
所以AB=BD+CF. 8分
20.解:(1)△ABC≌△DEF. 1分
理由:因为AF=CD,所以AF+FC=CD+FC,即AC=DF. 2分
因为AB∥DE,所以∠D=∠A. 3分
在△ABC和△DEF中,
所以△ABC≌△DEF. 5分
(2)平行且相等. 6分
理由:因为△ABC≌△DEF,所以∠EFC=∠FCB,EF=CB, 7分
所以FE∥CB. 8分
21.解:(1)85°. 3分
(2)因为BP⊥PC,
所以∠BPC=90°,
所以∠PBC+∠PCB=90°. 6分
因为BP,CP分别是∠ABC“邻BA三分线”和“∠ACB邻CA三分线”,
所以∠ABC+∠ACB=90°,
所以∠ABC+∠ACB=135°,
所以∠A=180°-(∠ABC+∠ACB)=45°. 9分
22.解:(1)证明:因为AD是BC边上的中线,
所以CD=BD.
在△ACD和△EBD中,
所以△ACD≌△EBD(SAS). 3分
(2)AD与BC的数量关系为AD=BC. 4分
理由如下:延长AD到点E,使DE=AD,连接BE,如图所示.
同(1)得△ACD≌△EBD(SAS),
所以AC=BE,∠DAC=∠DEB,
所以AC∥BE,
所以∠BAC+∠ABE=180°.
因为∠BAC=90°,
所以∠BAC=∠ABE=90°. 6分
在△BAC和△ABE中,
所以△BAC≌△ABE(SAS),
所以BC=AE.
因为AD=DE=AE,
所以AD=BC. 9分
23.解:(1)DE⊥AB. 2分
(2)①△BDE≌△CDF. 3分
理由:因为D是边BC的中点,
所以BD=CD.
因为E、F分别是边AB、AC的中点,
所以BE=AB,CF=AC.
又因为AB=AC,
所以BE=CF. 5分
在△BDE和△CDF中,
所以△BDE≌△CDF(SAS). 7分
②AG=AH. 8分
理由:因为∠AEG=∠BED+∠DEG-180°,
所以∠AEG=2∠BED-180°.
因为∠AFH=∠CFD+∠DFH-180°,
所以∠AFH=2∠CFD-180°.
因为△BDE≌△CDF,
所以∠BED=∠CFD,
所以∠AEG=∠AFH. 9分
因为AE=BE=GE=AB,AF=CF=HF=AC,AB=AC,
所以AE=AF,GE=HF. 10分
在△AEG和△AFH中,
所以△AEG≌△AFH(SAS),
所以AG=AH. 12分
(用其他方法说明理由,亦相应给分)
2
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
