2023-2024学年初中数学华东师大版八年级下册第17章 函数及其图象 单元练习 (含答案)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版八年级下册第17章 函数及其图象 单元练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 177.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 06:48:48 | ||
图片预览




文档简介
第17章 函数及其图象
(时间:100分钟 分值:120分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,请把正确答案的代号填入题后括号内.
1.函数y=中自变量x的取值范围是 ( )
A.x≥3 B.x≠-3 C.x≤3 D.x≠3
2.点A(m,-4)在函数y=-2x的图象上,则m的值为 ( )
A.-8 B.8 C.-2 D.2
3.已知点P的坐标为(-5,m2+1),则点P一定在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.将直线y=3x+1向下平移2个单位长度,平移后直线的表达式为 ( )
A.y=3x-1 B.y=-3x+1
C.y=3x+3 D.y=x-3
5.如图,反比例函数y=的图象如图所示,点A是该函数图象上的一点,AB垂直x轴于点B,若S△AOB=1,则k的值为 ( )
A.1 B.-1
C.2 D.-2
6.若一次函数y=kx+b(k≠0)的图象经过第一、三、四象限,则k,b满足 ( )
A.k>0,b<0 B.k>0,b>0
C.k<0,b>0 D.k<0,b<0
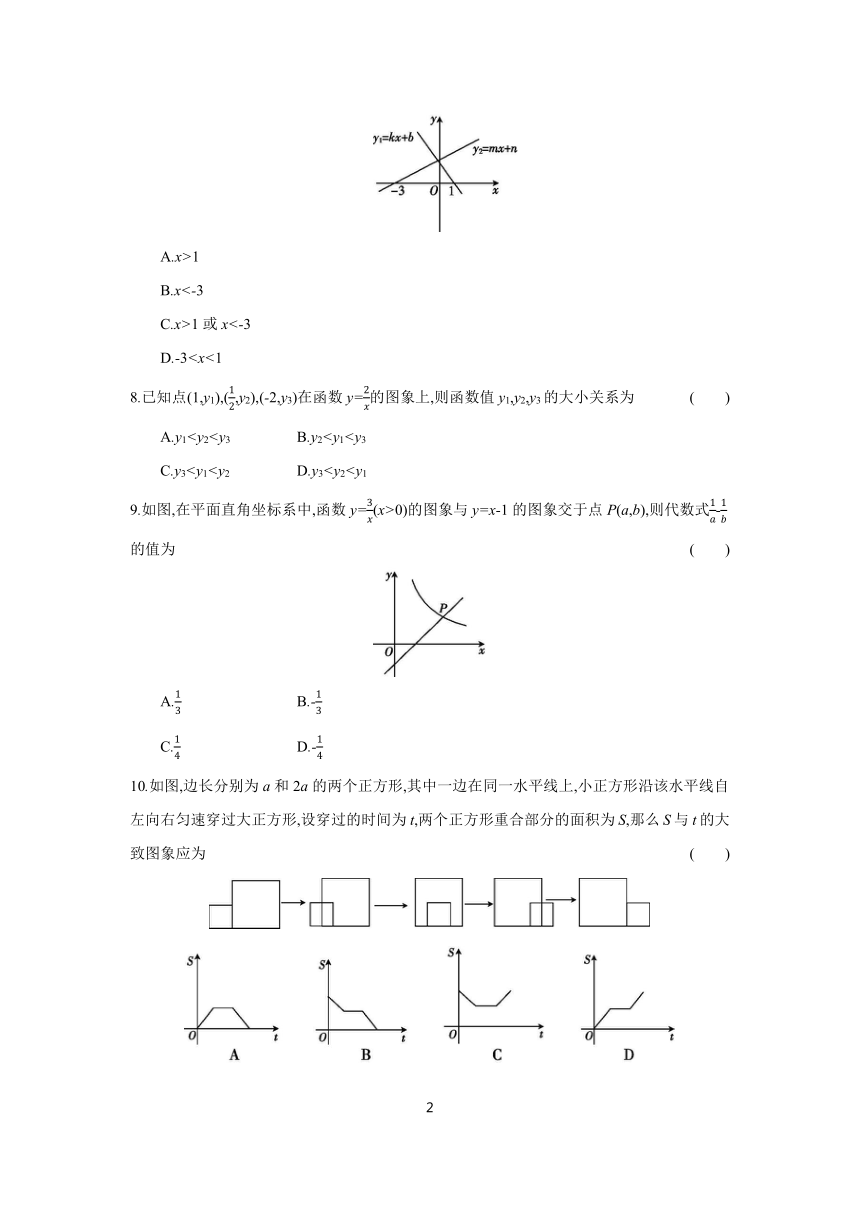
7.函数y1=kx+b与y2=mx+n的图象如图所示,则不等式组的解集为 ( )
A.x>1
B.x<-3
C.x>1或x<-3
D.-38.已知点(1,y1),(,y2),(-2,y3)在函数y=的图象上,则函数值y1,y2,y3的大小关系为 ( )
A.y1C.y39.如图,在平面直角坐标系中,函数y=(x>0)的图象与y=x-1的图象交于点P(a,b),则代数式-的值为 ( )
A. B.-
C. D.-
10.如图,边长分别为a和2a的两个正方形,其中一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,两个正方形重合部分的面积为S,那么S与t的大致图象应为 ( )
二、填空题(每小题3分,共15分)
11.若函数y=2x+(1-m)是正比例函数,则m的值是 .
12.一次函数y=-3x-9的图象与x轴交点的坐标是 .
13.如图,折线A-B-C是我市出租车所收费用y(元)与出租车行驶路程x(km)之间的函数关系图象,某乘客支付车费15.6元,则出租车行驶了 km.
14.三个反比例函数y=,y=,y=的图象如图所示,则k1,k2,k3的大小顺序为 .(用“<”连接)
15.过反比例函数y=(k>0)图象上一动点M作MN⊥x轴于点N,Q是直线MN上一点,且MQ=2MN,过点Q作QR∥x轴交该反比例函数图象于点R.若S△QRM=4,则k的值为 .
三、解答题(本大题共8个小题,满分75分)
16.(1)(5分)在平面直角坐标系中,点P的坐标为(1-a,2a-6),若点P在第三象限,且到x轴的距离为2,求点P的坐标.
(2)(5分)若函数y=-x+m的图象与y=4x-1的图象的交点在x轴上,求交点的坐标及m的值.
17.(9分)已知y=y1+y2,y1与x成正比例,y2与x成反比例,当x=1或2时,y的值都为9,请回答下面的问题.
(1)求y与x之间的函数关系式.
(2)当x=-3时,求y的值.
18.(9分)已知反比例函数y=(a为常数,且a≠-3).
(1)若在其图象的每个分支上,y随x的增大而增大,求a的取值范围.
(2)若y=的图象与一次函数y=-x+2的图象的一个交点的纵坐标是3,求a的值.
19.(9分)如图,在平面直角坐标系内,一次函数y=kx+b(k≠0)的图象与正比例函数y=-2x的图象相交于点A,且与x轴交于点B.
(1)求这个一次函数的表达式.
(2)求线段AB的长.
20.(9分)某游泳池有水4000 m3,需要放水清洗池子.已知工作人员记录的放水时间x(单位:分钟)与池内水量y(单位:m3) 的对应变化的情况如下表所示:
放水时间x(分钟) … 10 20 30 40 …
池内水量y(m3) … 3750 3500 3250 3000 …
(1)根据上表提供的信息,当放水到第80分钟时,池内有水多少m3
(2)请你用函数表达式表示y与x的关系,并写出自变量x的取值范围.
21.(9分)如图,反比例函数y=(x>0)与一次函数y=ax+b的图象交于C,D两点,若点D的坐标为(3,1),点C的横坐标为1,请回答下列问题:
(1)求△AOC的面积.
(2)利用图象求关于x的不等式>-x+4(x>0)的解集.
22.(10分)某体育用品商店,准备用不超过2800元购买足球和篮球共计60个,已知一个篮球的进价为50元,售价为65元;一个足球的进价为40元,售价为50元.
(1)若购进x个篮球,购买这批球共花费y元,求y与x之间的函数关系式.
(2)设售出这批球共盈利w元,求w与x之间的函数关系式.
(3)体育用品商店购进篮球和足球各多少个时,才能获得最大利润 最大利润是多少
23.(10分)如图,点A在函数y=(x>0)的图象上,过点A作x轴的平行线交函数y=(x<0)的图象于点B,若点A的坐标为(1,3),S△AOB=6.
(1)分别求这两个函数的表达式.
(2)若(a,b)在函数y=的图象上,试说明点(b,a)也在函数y=的图象上.
(3)若在函数y=(x>0)的图象上有一点C,使得OA=OC,试猜测点C的坐标并求直线BC的表达式.
参考答案
1.D 2.D 3.B 4.A 5.D 6.A 7.D 8.C 9.B 10.A
11.1 12.(-3,0) 13.10 14.k115.6或2 提示:①如图1,当点Q在第一象限时,设M(,m),则R(,3m),
由题意得×2m×(-)=4,
解得k=6.
②如图2,当点Q在第四象限时,设M(,m),则R(-,-m),
由题意得··2m=4,
解得k=2,
∴k=6或2.
当点M在第三象限时,同理可得k=6或2.
故答案为6或2.
16.(1)解:∵点P(1-a,2a-6)在第三象限,且到x轴的距离为2,
∴2a-6=-2,
解得a=2, 3分
∴1-a=1-2=-1, 4分
∴点P的坐标为(-1,-2). 5分
(2)解:依题意,得y=4x-1=0,解得x=,
∴交点的坐标是(,0). 3分
把(,0)代入y=-x+m,得m=,
∴m的值是. 5分
17.解:(1)设y1=mx,y2=,得y=mx+. 2分
∵当x=1或2时,y的值都为9,
∴解得
∴y=3x+. 6分
(2)将x=-3代入y=3x+,得
y=-9-2=-11. 9分
18.解:(1)∵y=在其图象的每个分支上,y随x的增大而增大,
∴a+3<0,
解得a<-3. 3分
(2)依题意,得3=-x+2,
解得x=-1,
故交点的坐标为(-1,3). 6分
∵反比例函数y=的图象也经过点(-1,3),
∴-1×3=a+3,
解得a=-6. 9分
19.解:(1)在函数y=-2x中,令y=2,得-2x=2,
解得x=-1,
∴点A的坐标为(-1,2). 1分
将点A(-1,2)、点B(1,0)代入y=kx+b,得
解得
∴一次函数的表达式为y=-x+1. 4分
(2)如图,过点A作AC垂直于x轴,垂足为C.
由点A为(-1,2)可知AC=2,OC=1, 6分
∴BC=2,
∴AB==2. 9分
20.解:(1)由表格可知,每10分钟放水250 m3,
∴第80分钟时,池内有水4000-8×250=2000 m3. 3分
(2)设函数表达式为y=kx+b, 4分
∵当x=20时,y=3500,
当x=40时,y=3000,
∴ 6分
解得
∴y=-25x+4000, 7分
自变量x的取值范围为0≤x≤160. 9分
21.解:(1)如图1,连接OC,
将(3,1)代入y=(x>0)得k=3,
∴反比例函数的表达式为y=(x>0). 2分
故点C的坐标为(1,3),又∵点D的坐标为(3,1),
∴可得a=-1,b=4,
∴直线y=-x+4,与y轴的交点坐标为(0,4),
∴S△AOC==2. 5分
(2)如图2,过交点C,D作y轴的平行线.
不等式>-x+4(x>0)表示反比例函数图象在一次函数图象上方的图象对应的x的值,
故由图可知, 关于x的不等式>-x+4(x>0)的解集为03. 9分
22.解:(1)若购进x个篮球,则购进(60-x)个足球.
y=50x+40(60-x)=10x+2400,
y与x之间的函数关系式为y=10x+2400. 3分
(2)w=(65-50)x+(50-40)(60-x)=15x+10(60-x)=5x+600,
w与x之间的函数关系式w=5x+600. 6分
(3)由题意可得10x+2400≤2800,
解得x≤40. 7分
在 w=5x+600中,
∵k=5>0,
∴y随x的增大而增大,
∴当x=40时,w取得最大值,此时w=800,60-x=20,
答:当购买40个篮球,20个足球时,获得的利润最大,最大利润为800. 10分
23.解:(1)如图,设点B的横坐标为xB.
∵函数y=(x>0)的图象经过点A(1,3),∴k1=1×3=3,∴y=(x>0). 1分
∵AB∥x轴,∴yA=yB=3,
∵S△AOB=6,∴ =6,解得xB=-3.
∵函数y=(x<0)的图象过点B(-3,3),∴ k2=-9,∴ y=-(x<0). 3分
(2)∵点(a,b)在y=-的图象上,
∴ab=-9,
将x=b代人y=-,
得y=-=a,
故点(b,a)也在y=-的图象上. 6分
(3)∵反比例函数关于y=x对称,猜测点C的坐标为(3,1),将其代入y=成立,且OA==OC,
∴点C的坐标为(3,1). 8分
设直线BC的表达式为y=kx+b,则解得
∴y=-x+2. 10分
2
(时间:100分钟 分值:120分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,请把正确答案的代号填入题后括号内.
1.函数y=中自变量x的取值范围是 ( )
A.x≥3 B.x≠-3 C.x≤3 D.x≠3
2.点A(m,-4)在函数y=-2x的图象上,则m的值为 ( )
A.-8 B.8 C.-2 D.2
3.已知点P的坐标为(-5,m2+1),则点P一定在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.将直线y=3x+1向下平移2个单位长度,平移后直线的表达式为 ( )
A.y=3x-1 B.y=-3x+1
C.y=3x+3 D.y=x-3
5.如图,反比例函数y=的图象如图所示,点A是该函数图象上的一点,AB垂直x轴于点B,若S△AOB=1,则k的值为 ( )
A.1 B.-1
C.2 D.-2
6.若一次函数y=kx+b(k≠0)的图象经过第一、三、四象限,则k,b满足 ( )
A.k>0,b<0 B.k>0,b>0
C.k<0,b>0 D.k<0,b<0
7.函数y1=kx+b与y2=mx+n的图象如图所示,则不等式组的解集为 ( )
A.x>1
B.x<-3
C.x>1或x<-3
D.-3
A.y1
A. B.-
C. D.-
10.如图,边长分别为a和2a的两个正方形,其中一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,两个正方形重合部分的面积为S,那么S与t的大致图象应为 ( )
二、填空题(每小题3分,共15分)
11.若函数y=2x+(1-m)是正比例函数,则m的值是 .
12.一次函数y=-3x-9的图象与x轴交点的坐标是 .
13.如图,折线A-B-C是我市出租车所收费用y(元)与出租车行驶路程x(km)之间的函数关系图象,某乘客支付车费15.6元,则出租车行驶了 km.
14.三个反比例函数y=,y=,y=的图象如图所示,则k1,k2,k3的大小顺序为 .(用“<”连接)
15.过反比例函数y=(k>0)图象上一动点M作MN⊥x轴于点N,Q是直线MN上一点,且MQ=2MN,过点Q作QR∥x轴交该反比例函数图象于点R.若S△QRM=4,则k的值为 .
三、解答题(本大题共8个小题,满分75分)
16.(1)(5分)在平面直角坐标系中,点P的坐标为(1-a,2a-6),若点P在第三象限,且到x轴的距离为2,求点P的坐标.
(2)(5分)若函数y=-x+m的图象与y=4x-1的图象的交点在x轴上,求交点的坐标及m的值.
17.(9分)已知y=y1+y2,y1与x成正比例,y2与x成反比例,当x=1或2时,y的值都为9,请回答下面的问题.
(1)求y与x之间的函数关系式.
(2)当x=-3时,求y的值.
18.(9分)已知反比例函数y=(a为常数,且a≠-3).
(1)若在其图象的每个分支上,y随x的增大而增大,求a的取值范围.
(2)若y=的图象与一次函数y=-x+2的图象的一个交点的纵坐标是3,求a的值.
19.(9分)如图,在平面直角坐标系内,一次函数y=kx+b(k≠0)的图象与正比例函数y=-2x的图象相交于点A,且与x轴交于点B.
(1)求这个一次函数的表达式.
(2)求线段AB的长.
20.(9分)某游泳池有水4000 m3,需要放水清洗池子.已知工作人员记录的放水时间x(单位:分钟)与池内水量y(单位:m3) 的对应变化的情况如下表所示:
放水时间x(分钟) … 10 20 30 40 …
池内水量y(m3) … 3750 3500 3250 3000 …
(1)根据上表提供的信息,当放水到第80分钟时,池内有水多少m3
(2)请你用函数表达式表示y与x的关系,并写出自变量x的取值范围.
21.(9分)如图,反比例函数y=(x>0)与一次函数y=ax+b的图象交于C,D两点,若点D的坐标为(3,1),点C的横坐标为1,请回答下列问题:
(1)求△AOC的面积.
(2)利用图象求关于x的不等式>-x+4(x>0)的解集.
22.(10分)某体育用品商店,准备用不超过2800元购买足球和篮球共计60个,已知一个篮球的进价为50元,售价为65元;一个足球的进价为40元,售价为50元.
(1)若购进x个篮球,购买这批球共花费y元,求y与x之间的函数关系式.
(2)设售出这批球共盈利w元,求w与x之间的函数关系式.
(3)体育用品商店购进篮球和足球各多少个时,才能获得最大利润 最大利润是多少
23.(10分)如图,点A在函数y=(x>0)的图象上,过点A作x轴的平行线交函数y=(x<0)的图象于点B,若点A的坐标为(1,3),S△AOB=6.
(1)分别求这两个函数的表达式.
(2)若(a,b)在函数y=的图象上,试说明点(b,a)也在函数y=的图象上.
(3)若在函数y=(x>0)的图象上有一点C,使得OA=OC,试猜测点C的坐标并求直线BC的表达式.
参考答案
1.D 2.D 3.B 4.A 5.D 6.A 7.D 8.C 9.B 10.A
11.1 12.(-3,0) 13.10 14.k1
由题意得×2m×(-)=4,
解得k=6.
②如图2,当点Q在第四象限时,设M(,m),则R(-,-m),
由题意得··2m=4,
解得k=2,
∴k=6或2.
当点M在第三象限时,同理可得k=6或2.
故答案为6或2.
16.(1)解:∵点P(1-a,2a-6)在第三象限,且到x轴的距离为2,
∴2a-6=-2,
解得a=2, 3分
∴1-a=1-2=-1, 4分
∴点P的坐标为(-1,-2). 5分
(2)解:依题意,得y=4x-1=0,解得x=,
∴交点的坐标是(,0). 3分
把(,0)代入y=-x+m,得m=,
∴m的值是. 5分
17.解:(1)设y1=mx,y2=,得y=mx+. 2分
∵当x=1或2时,y的值都为9,
∴解得
∴y=3x+. 6分
(2)将x=-3代入y=3x+,得
y=-9-2=-11. 9分
18.解:(1)∵y=在其图象的每个分支上,y随x的增大而增大,
∴a+3<0,
解得a<-3. 3分
(2)依题意,得3=-x+2,
解得x=-1,
故交点的坐标为(-1,3). 6分
∵反比例函数y=的图象也经过点(-1,3),
∴-1×3=a+3,
解得a=-6. 9分
19.解:(1)在函数y=-2x中,令y=2,得-2x=2,
解得x=-1,
∴点A的坐标为(-1,2). 1分
将点A(-1,2)、点B(1,0)代入y=kx+b,得
解得
∴一次函数的表达式为y=-x+1. 4分
(2)如图,过点A作AC垂直于x轴,垂足为C.
由点A为(-1,2)可知AC=2,OC=1, 6分
∴BC=2,
∴AB==2. 9分
20.解:(1)由表格可知,每10分钟放水250 m3,
∴第80分钟时,池内有水4000-8×250=2000 m3. 3分
(2)设函数表达式为y=kx+b, 4分
∵当x=20时,y=3500,
当x=40时,y=3000,
∴ 6分
解得
∴y=-25x+4000, 7分
自变量x的取值范围为0≤x≤160. 9分
21.解:(1)如图1,连接OC,
将(3,1)代入y=(x>0)得k=3,
∴反比例函数的表达式为y=(x>0). 2分
故点C的坐标为(1,3),又∵点D的坐标为(3,1),
∴可得a=-1,b=4,
∴直线y=-x+4,与y轴的交点坐标为(0,4),
∴S△AOC==2. 5分
(2)如图2,过交点C,D作y轴的平行线.
不等式>-x+4(x>0)表示反比例函数图象在一次函数图象上方的图象对应的x的值,
故由图可知, 关于x的不等式>-x+4(x>0)的解集为0
22.解:(1)若购进x个篮球,则购进(60-x)个足球.
y=50x+40(60-x)=10x+2400,
y与x之间的函数关系式为y=10x+2400. 3分
(2)w=(65-50)x+(50-40)(60-x)=15x+10(60-x)=5x+600,
w与x之间的函数关系式w=5x+600. 6分
(3)由题意可得10x+2400≤2800,
解得x≤40. 7分
在 w=5x+600中,
∵k=5>0,
∴y随x的增大而增大,
∴当x=40时,w取得最大值,此时w=800,60-x=20,
答:当购买40个篮球,20个足球时,获得的利润最大,最大利润为800. 10分
23.解:(1)如图,设点B的横坐标为xB.
∵函数y=(x>0)的图象经过点A(1,3),∴k1=1×3=3,∴y=(x>0). 1分
∵AB∥x轴,∴yA=yB=3,
∵S△AOB=6,∴ =6,解得xB=-3.
∵函数y=(x<0)的图象过点B(-3,3),∴ k2=-9,∴ y=-(x<0). 3分
(2)∵点(a,b)在y=-的图象上,
∴ab=-9,
将x=b代人y=-,
得y=-=a,
故点(b,a)也在y=-的图象上. 6分
(3)∵反比例函数关于y=x对称,猜测点C的坐标为(3,1),将其代入y=成立,且OA==OC,
∴点C的坐标为(3,1). 8分
设直线BC的表达式为y=kx+b,则解得
∴y=-x+2. 10分
2
