2023-2024学年初中数学华东师大版八年级下册第18章 平行四边形 单元练习(含答案)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版八年级下册第18章 平行四边形 单元练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 245.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 06:49:16 | ||
图片预览




文档简介
第18章 平行四边形
(时间:100分钟 分值:120分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,请把正确答案的代号填入题后括号内.
1.在平行四边形ABCD中,∠A=2∠B,则∠B等于 ( )
A.45° B.60° C.90° D.120°
2.如图,在 ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为 ( )
A.6 B.15
C.30 D.60
3.如图,在平行四边形ABCD中,DE⊥AB于点E,且∠EDA=25°,则∠C等于 ( )
A.25° B.55°
C.65° D.75°
4.如图, ABCD的对角线AC,BD相交于点O,已知AD=10,BD=14,AC=8,则△OBC的周长为 ( )
A.16
B.19
C.21
D.28
5.如图,在平行四边形ABCD中,E,F分别为AD,BC边上的一点,则增加下列某个条件,不一定能得出BE∥DF的是 ( )
A.AE=CF
B.BE=DF
C.∠EBF=∠FDE
D.∠BED=∠BFD
6.如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AD于点F,则∠1等于 ( )
A.40°
B.50°
C.60°
D.80°
7.如图,在平行四边形ABCD中,E是AB边上一点,连接DE,CE.若DE,CE分别是∠ADC,∠BCD的平分线,且AB=4,则平行四边形ABCD的周长为 ( )
A.10 B.8 C.5 D.12
8.在四边形ABCD中,对角线AC,BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判定这个四边形是平行四边形的条件有 ( )
A.1组 B.2组 C.3组 D.4组
9.如图,在等边三角形ABC中,AB=6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.如果点E,F同时出发,当以点A,E,C,F为顶点的四边形是平行四边形时,那么运动时间t的值为 ( )
A.2 s B.6 s
C.8 s D.2 s或6 s
10.如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE,则图中与△ACE全等的三角形还有 ( )
A.△DCE
B.△DCE,△ABD
C.△BCD,△ACE
D.△DCE,△ABD,△ABE
二、填空题(每小题3分,共15分)
11.如图, ABCD的对角线AC和BD交于点O,若AC=6,BD=10,AB=4,则 ABCD的面积等于 .
12.如图,在 ABCD中,E是BC边上一点,且AB=AE,若AE平分∠DAB,∠EAC=27°,则∠AED的度数为 .
13.以不共线的三点A,B,C为平行四边形的三个顶点作平行四边形,则第四个顶点的位置有 处.
14.如图,在 ABCD中,点E在边AD上,以BE为折痕,将△ABE沿BE翻折,点A正好落在CD上的点F处,若△FDE的周长为8,△FCB的周长为22,则FC的长为 .
15.在平行四边形ABCD中,边AB=15,对角线AC=13,BC边上的高为12,则平行四边形ABCD的面积为 .
三、解答题(本大题共8个小题,满分75分)
16.(1)(5分)如图,平行四边形ABCD的对角线AC,BD相交于点O,若AC=16 cm,BD=32 cm,CD=15 cm,求△AOB的周长.
(2)(5分)如图,在 ABCD中,点E,F分别在AD,BC上,且AE=CF,连接EF交AC于点O,求证:OE=OF.
17.(9分)如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
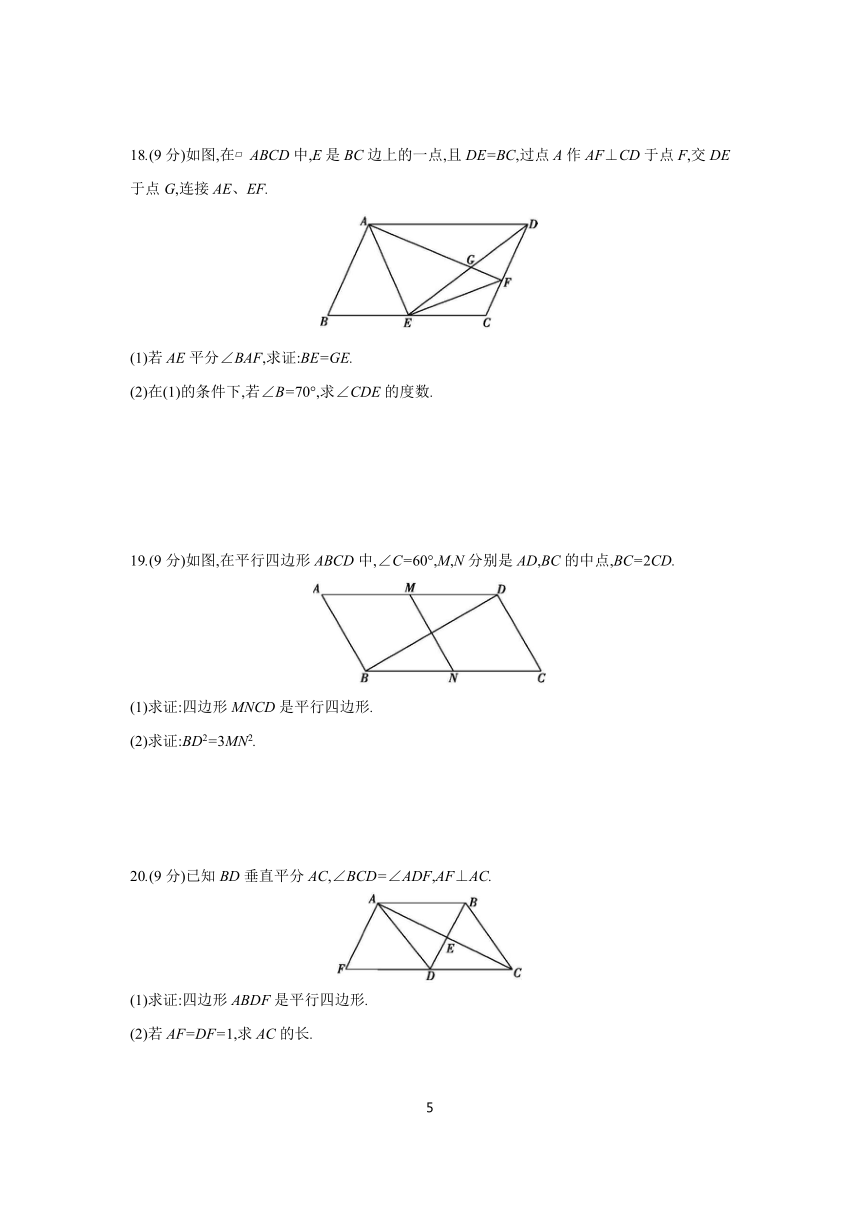
18.(9分)如图,在 ABCD中,E是BC边上的一点,且DE=BC,过点A作AF⊥CD于点F,交DE于点G,连接AE、EF.
(1)若AE平分∠BAF,求证:BE=GE.
(2)在(1)的条件下,若∠B=70°,求∠CDE的度数.
19.(9分)如图,在平行四边形ABCD中,∠C=60°,M,N分别是AD,BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形.
(2)求证:BD2=3MN2.
20.(9分)已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC.
(1)求证:四边形ABDF是平行四边形.
(2)若AF=DF=1,求AC的长.
21.(9分)如图,在 ABCD中,∠BAD=32°,分别以BC,CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E,C两点之间,连接AE,AF.
(1)求证:△ABE≌△FDA.
(2)当AE⊥AF时,求∠EBH的度数.
22.(10分)如图,BD是四边形ABCD的对角线,AB=CD=3 cm,AD=BC=5 cm,动点P,Q均以1 cm/s的速度分别从B,D同时出发,点P沿B→C→D向终点D匀速运动,点Q沿D→A→B向终点B匀速运动,连接PQ交BD于点O,设点P的运动时间为t(s).
(1)求证:AD∥BC.
(2)求证:OB=OD.
(3)当CP的长是四边形ABCD一边长的一半时,求t的值.
(4)连接AP,若直线AP将四边形ABCD的面积分成1∶2的两部分,直接写出t的值.
23.(10分)分别以 ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形△ABE,△CDG,△ADF.
(1)如图1,当三个等腰直角三角形都在该平行四边形的外部时,连接GF,EF,请判断GF与EF的关系.
(2)如图2,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,则(1)中的结论还成立吗 若成立,请给出证明;若不成立,请说明理由.
参考答案
1.B 2.C 3.C 4.C 5.B 6.B 7.D 8.C 9.D 10.D
11.24 12.87° 13.3 14.7
15.168或48 提示:∵AB=15,AC=13,BC边上的高是12,即AE=12.
在Rt△ABE中,BE==9,
在Rt△ACE中,CE==5,
如图1,BC=BE+CE=14,
∴平行四边形ABCD的面积为BC·AE=14×12=168.
如图2,BC=BE-CE=4,
∴平行四边形ABCD的面积为BC·AE=4×12=48,
综上所述,平行四边形ABCD的面积为168或48.
故答案为168或48.
16.(1)解:∵四边形ABCD为平行四边形,
∴AO=CO,BO=DO,AB=CD=15 cm. 2分
∵AC=16 cm,BD=32 cm,
∴AO=CO=8 cm,BO=DO=16 cm, 4分
∴△ABO的周长为AB+BO+AO=15+16+8=39(cm). 5分
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEO=∠CFO. 2分
在△AEO和△CFO中,
∴△AEO≌△CFO(AAS),
∴OE=OF. 5分
17.解:四边形ABFC是平行四边形. 1分
证明如下:
∵AB∥CD,∴∠BAE=∠CFE.
∵E是BC的中点,∴BE=CE.
在△ABE和△FCE中,
∴△ABE≌△FCE(AAS), 7分
∴AE=EF,又∵BE=CE,∴四边形ABFC是平行四边形. 9分
18.解:(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠DAE=∠AEB.
∵DE=BC,∴AD=DE,∴∠DAE=∠AED,∴∠AEB=∠AED.
∵AE平分∠BAF,∴∠BAE=∠GAE.
在△ABE和△AGE中,
∴△ABE≌△AGE(ASA),∴BE=GE. 5分
(2)由(1)可知△ABE≌△AGE,∴∠B=∠EGA=70°,∴∠DGF=∠EGA=70°.
∵AF⊥CD,∴∠GFD=90°,∴∠GDF+∠DGF=90°,∴∠CDE=90°-70°=20°. 9分
19.证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∵M,N分别是AD,BC的中点,∴MD=NC,MD∥NC,∴四边形MNCD是平行四边形. 4分
(2)如图,连接DN.
∵N是BC的中点,BC=2CD,∴CD=NC.
又∵∠C=60°,∴△DCN是等边三角形,
∴ND=NC,∠DNC=∠NDC=60°,
∴ND=NB=CN,∴∠DBC=∠BDN=30°,∴∠BDC=∠BDN+∠NDC=90°,
∴BD2=BC2-CD2=3CD2.
∵四边形MNCD是平行四边形,∴MN=CD,∴BD2=3MN2. 9分
20.解:(1)证明:∵BD垂直平分AC,∴AB=BC,AD=DC,∴∠BAC=∠BCA,∠DAC=∠DCA,
∴∠BAD=∠BCD.
∵∠BCD=∠ADF,∴∠BAD=∠ADF,∴AB∥FD.
∵BD⊥AC,AF⊥AC,∴AF∥BD,∴四边形ABDF是平行四边形. 4分
(2)∵四边形ABDF是平行四边形,∴AB∥CD,DF=AB=1.
∵E为AC的中点,
∴易证△ABE≌△CDE,
∴CD=AB=1,
∴CF=2.
∵AF⊥AC,
∴AC2=CF2-AF2,
∴AC=. 9分
21.解:(1)证明:在 ABCD中,BC=AD,
CD=AB,∠ABC=∠ADC,
又∵BE=BC,DF=DC,∠EBC=∠CDF,
∴AD=BE,DF=AB,∠ADF=∠ABE,
∴△ABE≌△FDA. 4分
(2)∵AE⊥AF,∠DAB=32°,
∴∠FAD+∠EAB=58°.
∵△ABE≌△FDA,
∴∠FAD=∠AEB,
∴∠AEB+∠EAB=58°.
∵∠EBH=∠AEB+∠EAB,
∴∠EBH=58°. 9分
22.证明:(1)∵AB=CD=3 cm,AD=BC=5 cm,∴四边形ABCD为平行四边形,
∴AD∥BC. 2分
(2)∵动点P,Q均以1 cm/s的速度分别从B,D同时出发,∴DQ=BP,∵AD∥BC,∴∠OBP=∠ODQ,∠BPO=∠DQO,
∴△BOP≌△DOQ,∴OB=OD. 5分
(3)当0≤t≤5时,CP=2.5 cm或CP=1.5 cm,∴t=2.5或t=3.5;
当5(4)t的值为或6. 10分
23.解:(1)GF=EF.理由如下:
∵四边形ABCD是平行四边形,∴CD=BA.
∵△CDG和△BAE分别是以CD和BA为斜边的等腰直角三角形,∴DG=AE.
在△GDF中,∠GDF=∠GDC+∠FDA+∠CDA=90°+∠CDA.
在△EAF中,∠EAF=360°-∠BAD-∠BAE-∠DAF=360°-(180°-∠CDA)-90°=90°+∠CDA.
在△GDF和△EAF中,
∴△GDF≌△EAF,∴GF=EF. 5分
(2)成立,证明如下:
∵四边形ABCD是平行四边形,∴CD=BA.
∵△CDG和△BAE分别是以CD和BA为斜边的等腰直角三角形,
∴DG=AE.
在△GDF中,∠GDF=∠GDC+∠FDA-∠CDA=90°-∠CDA.
在△EAF中,∠EAF=∠BAD-∠BAE-∠DAF=180°-∠CDA-90°=90°-∠CDA.
在△GDF和△EAF中,
∴△GDF≌△EAF,∴GF=EF. 10分
2
(时间:100分钟 分值:120分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,请把正确答案的代号填入题后括号内.
1.在平行四边形ABCD中,∠A=2∠B,则∠B等于 ( )
A.45° B.60° C.90° D.120°
2.如图,在 ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为 ( )
A.6 B.15
C.30 D.60
3.如图,在平行四边形ABCD中,DE⊥AB于点E,且∠EDA=25°,则∠C等于 ( )
A.25° B.55°
C.65° D.75°
4.如图, ABCD的对角线AC,BD相交于点O,已知AD=10,BD=14,AC=8,则△OBC的周长为 ( )
A.16
B.19
C.21
D.28
5.如图,在平行四边形ABCD中,E,F分别为AD,BC边上的一点,则增加下列某个条件,不一定能得出BE∥DF的是 ( )
A.AE=CF
B.BE=DF
C.∠EBF=∠FDE
D.∠BED=∠BFD
6.如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AD于点F,则∠1等于 ( )
A.40°
B.50°
C.60°
D.80°
7.如图,在平行四边形ABCD中,E是AB边上一点,连接DE,CE.若DE,CE分别是∠ADC,∠BCD的平分线,且AB=4,则平行四边形ABCD的周长为 ( )
A.10 B.8 C.5 D.12
8.在四边形ABCD中,对角线AC,BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判定这个四边形是平行四边形的条件有 ( )
A.1组 B.2组 C.3组 D.4组
9.如图,在等边三角形ABC中,AB=6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,点F从点B出发沿射线BC以2 cm/s的速度运动.如果点E,F同时出发,当以点A,E,C,F为顶点的四边形是平行四边形时,那么运动时间t的值为 ( )
A.2 s B.6 s
C.8 s D.2 s或6 s
10.如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE,则图中与△ACE全等的三角形还有 ( )
A.△DCE
B.△DCE,△ABD
C.△BCD,△ACE
D.△DCE,△ABD,△ABE
二、填空题(每小题3分,共15分)
11.如图, ABCD的对角线AC和BD交于点O,若AC=6,BD=10,AB=4,则 ABCD的面积等于 .
12.如图,在 ABCD中,E是BC边上一点,且AB=AE,若AE平分∠DAB,∠EAC=27°,则∠AED的度数为 .
13.以不共线的三点A,B,C为平行四边形的三个顶点作平行四边形,则第四个顶点的位置有 处.
14.如图,在 ABCD中,点E在边AD上,以BE为折痕,将△ABE沿BE翻折,点A正好落在CD上的点F处,若△FDE的周长为8,△FCB的周长为22,则FC的长为 .
15.在平行四边形ABCD中,边AB=15,对角线AC=13,BC边上的高为12,则平行四边形ABCD的面积为 .
三、解答题(本大题共8个小题,满分75分)
16.(1)(5分)如图,平行四边形ABCD的对角线AC,BD相交于点O,若AC=16 cm,BD=32 cm,CD=15 cm,求△AOB的周长.
(2)(5分)如图,在 ABCD中,点E,F分别在AD,BC上,且AE=CF,连接EF交AC于点O,求证:OE=OF.
17.(9分)如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
18.(9分)如图,在 ABCD中,E是BC边上的一点,且DE=BC,过点A作AF⊥CD于点F,交DE于点G,连接AE、EF.
(1)若AE平分∠BAF,求证:BE=GE.
(2)在(1)的条件下,若∠B=70°,求∠CDE的度数.
19.(9分)如图,在平行四边形ABCD中,∠C=60°,M,N分别是AD,BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形.
(2)求证:BD2=3MN2.
20.(9分)已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC.
(1)求证:四边形ABDF是平行四边形.
(2)若AF=DF=1,求AC的长.
21.(9分)如图,在 ABCD中,∠BAD=32°,分别以BC,CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E,C两点之间,连接AE,AF.
(1)求证:△ABE≌△FDA.
(2)当AE⊥AF时,求∠EBH的度数.
22.(10分)如图,BD是四边形ABCD的对角线,AB=CD=3 cm,AD=BC=5 cm,动点P,Q均以1 cm/s的速度分别从B,D同时出发,点P沿B→C→D向终点D匀速运动,点Q沿D→A→B向终点B匀速运动,连接PQ交BD于点O,设点P的运动时间为t(s).
(1)求证:AD∥BC.
(2)求证:OB=OD.
(3)当CP的长是四边形ABCD一边长的一半时,求t的值.
(4)连接AP,若直线AP将四边形ABCD的面积分成1∶2的两部分,直接写出t的值.
23.(10分)分别以 ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形△ABE,△CDG,△ADF.
(1)如图1,当三个等腰直角三角形都在该平行四边形的外部时,连接GF,EF,请判断GF与EF的关系.
(2)如图2,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,则(1)中的结论还成立吗 若成立,请给出证明;若不成立,请说明理由.
参考答案
1.B 2.C 3.C 4.C 5.B 6.B 7.D 8.C 9.D 10.D
11.24 12.87° 13.3 14.7
15.168或48 提示:∵AB=15,AC=13,BC边上的高是12,即AE=12.
在Rt△ABE中,BE==9,
在Rt△ACE中,CE==5,
如图1,BC=BE+CE=14,
∴平行四边形ABCD的面积为BC·AE=14×12=168.
如图2,BC=BE-CE=4,
∴平行四边形ABCD的面积为BC·AE=4×12=48,
综上所述,平行四边形ABCD的面积为168或48.
故答案为168或48.
16.(1)解:∵四边形ABCD为平行四边形,
∴AO=CO,BO=DO,AB=CD=15 cm. 2分
∵AC=16 cm,BD=32 cm,
∴AO=CO=8 cm,BO=DO=16 cm, 4分
∴△ABO的周长为AB+BO+AO=15+16+8=39(cm). 5分
(2)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEO=∠CFO. 2分
在△AEO和△CFO中,
∴△AEO≌△CFO(AAS),
∴OE=OF. 5分
17.解:四边形ABFC是平行四边形. 1分
证明如下:
∵AB∥CD,∴∠BAE=∠CFE.
∵E是BC的中点,∴BE=CE.
在△ABE和△FCE中,
∴△ABE≌△FCE(AAS), 7分
∴AE=EF,又∵BE=CE,∴四边形ABFC是平行四边形. 9分
18.解:(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠DAE=∠AEB.
∵DE=BC,∴AD=DE,∴∠DAE=∠AED,∴∠AEB=∠AED.
∵AE平分∠BAF,∴∠BAE=∠GAE.
在△ABE和△AGE中,
∴△ABE≌△AGE(ASA),∴BE=GE. 5分
(2)由(1)可知△ABE≌△AGE,∴∠B=∠EGA=70°,∴∠DGF=∠EGA=70°.
∵AF⊥CD,∴∠GFD=90°,∴∠GDF+∠DGF=90°,∴∠CDE=90°-70°=20°. 9分
19.证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∵M,N分别是AD,BC的中点,∴MD=NC,MD∥NC,∴四边形MNCD是平行四边形. 4分
(2)如图,连接DN.
∵N是BC的中点,BC=2CD,∴CD=NC.
又∵∠C=60°,∴△DCN是等边三角形,
∴ND=NC,∠DNC=∠NDC=60°,
∴ND=NB=CN,∴∠DBC=∠BDN=30°,∴∠BDC=∠BDN+∠NDC=90°,
∴BD2=BC2-CD2=3CD2.
∵四边形MNCD是平行四边形,∴MN=CD,∴BD2=3MN2. 9分
20.解:(1)证明:∵BD垂直平分AC,∴AB=BC,AD=DC,∴∠BAC=∠BCA,∠DAC=∠DCA,
∴∠BAD=∠BCD.
∵∠BCD=∠ADF,∴∠BAD=∠ADF,∴AB∥FD.
∵BD⊥AC,AF⊥AC,∴AF∥BD,∴四边形ABDF是平行四边形. 4分
(2)∵四边形ABDF是平行四边形,∴AB∥CD,DF=AB=1.
∵E为AC的中点,
∴易证△ABE≌△CDE,
∴CD=AB=1,
∴CF=2.
∵AF⊥AC,
∴AC2=CF2-AF2,
∴AC=. 9分
21.解:(1)证明:在 ABCD中,BC=AD,
CD=AB,∠ABC=∠ADC,
又∵BE=BC,DF=DC,∠EBC=∠CDF,
∴AD=BE,DF=AB,∠ADF=∠ABE,
∴△ABE≌△FDA. 4分
(2)∵AE⊥AF,∠DAB=32°,
∴∠FAD+∠EAB=58°.
∵△ABE≌△FDA,
∴∠FAD=∠AEB,
∴∠AEB+∠EAB=58°.
∵∠EBH=∠AEB+∠EAB,
∴∠EBH=58°. 9分
22.证明:(1)∵AB=CD=3 cm,AD=BC=5 cm,∴四边形ABCD为平行四边形,
∴AD∥BC. 2分
(2)∵动点P,Q均以1 cm/s的速度分别从B,D同时出发,∴DQ=BP,∵AD∥BC,∴∠OBP=∠ODQ,∠BPO=∠DQO,
∴△BOP≌△DOQ,∴OB=OD. 5分
(3)当0≤t≤5时,CP=2.5 cm或CP=1.5 cm,∴t=2.5或t=3.5;
当5
23.解:(1)GF=EF.理由如下:
∵四边形ABCD是平行四边形,∴CD=BA.
∵△CDG和△BAE分别是以CD和BA为斜边的等腰直角三角形,∴DG=AE.
在△GDF中,∠GDF=∠GDC+∠FDA+∠CDA=90°+∠CDA.
在△EAF中,∠EAF=360°-∠BAD-∠BAE-∠DAF=360°-(180°-∠CDA)-90°=90°+∠CDA.
在△GDF和△EAF中,
∴△GDF≌△EAF,∴GF=EF. 5分
(2)成立,证明如下:
∵四边形ABCD是平行四边形,∴CD=BA.
∵△CDG和△BAE分别是以CD和BA为斜边的等腰直角三角形,
∴DG=AE.
在△GDF中,∠GDF=∠GDC+∠FDA-∠CDA=90°-∠CDA.
在△EAF中,∠EAF=∠BAD-∠BAE-∠DAF=180°-∠CDA-90°=90°-∠CDA.
在△GDF和△EAF中,
∴△GDF≌△EAF,∴GF=EF. 10分
2
