2023-2024学年初中数学华东师大版八年级下册第19章 矩形、菱形与正方形 单元练习 (含答案)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版八年级下册第19章 矩形、菱形与正方形 单元练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 207.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 06:50:05 | ||
图片预览



文档简介
第19章 矩形、菱形与正方形
(时间:100分钟 分值:120分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,请把正确答案的代号填入题后括号内.
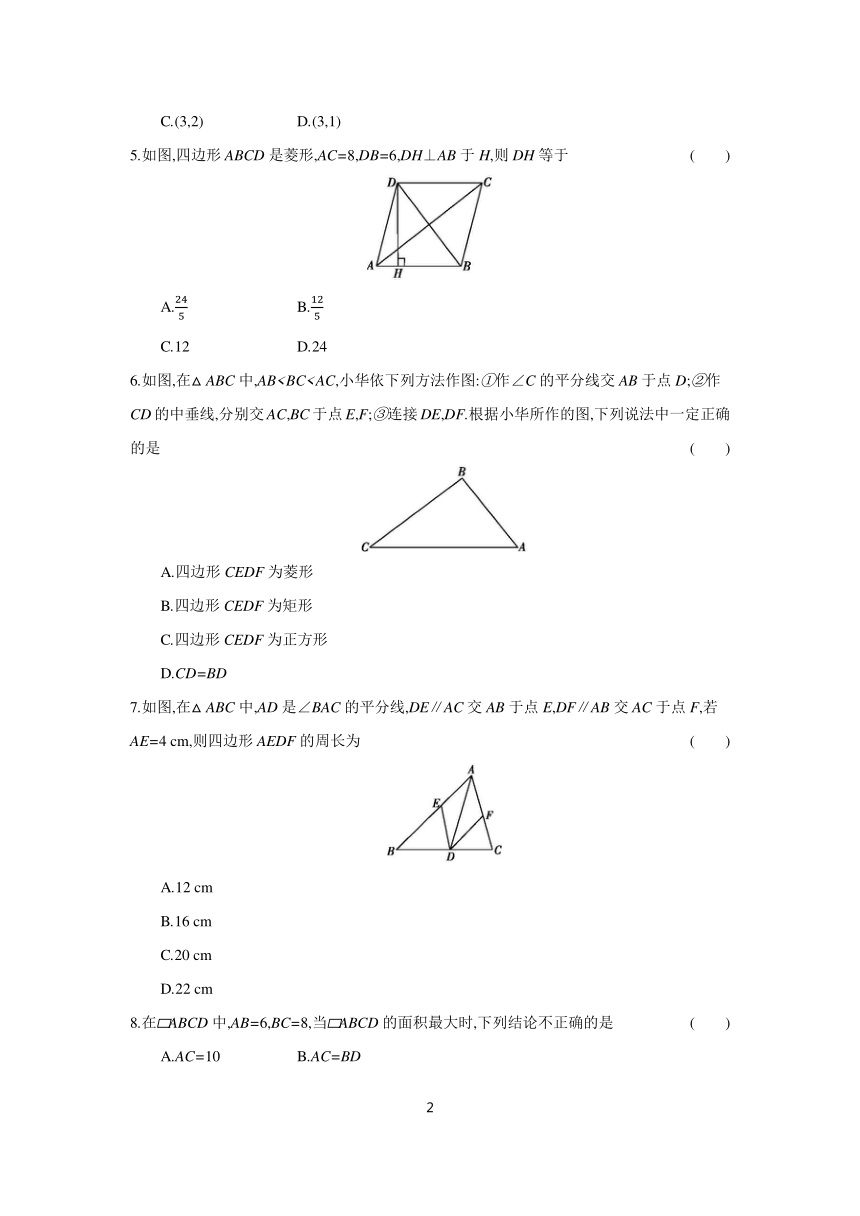
1.若菱形的一条边长为1,则该菱形的周长为 ( )
A.2 B.3 C.4 D.6
2.在图中所示的 ABCD中,再添加下列某一个条件,不能判定 ABCD是矩形的是 ( )
A.AC=BD
B.AB⊥BC
C.∠1=∠2
D.∠ABC=∠BCD
3.如图,在正方形ABCD中,在BA延长线上取一点E,使BE=BD,连接DE,则∠EDA的度数为 ( )
A.10°
B.15°
C.30°
D.22.5°
4.如图,在正方形OABC中,点A的坐标是(-3,1),则点C的坐标是 ( )
A.(1,3) B.(2,3)
C.(3,2) D.(3,1)
5.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于 ( )
A. B.
C.12 D.24
6.如图,在△ABC中,ABA.四边形CEDF为菱形
B.四边形CEDF为矩形
C.四边形CEDF为正方形
D.CD=BD
7.如图,在△ABC中,AD是∠BAC的平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,若AE=4 cm,则四边形AEDF的周长为 ( )
A.12 cm
B.16 cm
C.20 cm
D.22 cm
8.在 ABCD中,AB=6,BC=8,当 ABCD的面积最大时,下列结论不正确的是 ( )
A.AC=10 B.AC=BD
C.AC⊥BD D.∠A+∠C=180°
9.四边形ABCD的对角线AC和BD相交于点O,有下列条件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD.则下列推理不成立的是 ( )
A.①④ ⑥ B.①③ ⑤
C.①② ⑥ D.②③ ④
10.如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD,BD,有下列结论:①AD=BC;②BD,AC互相平分;③四边形ACED是菱形;④BD⊥DE.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题3分,共15分)
11.正方形ABCD的对角线AC=2,则边长AB= .
12.如图,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M的坐标是 .
13.如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转到能与△CBP'重合,若PB=1,则PP'= .
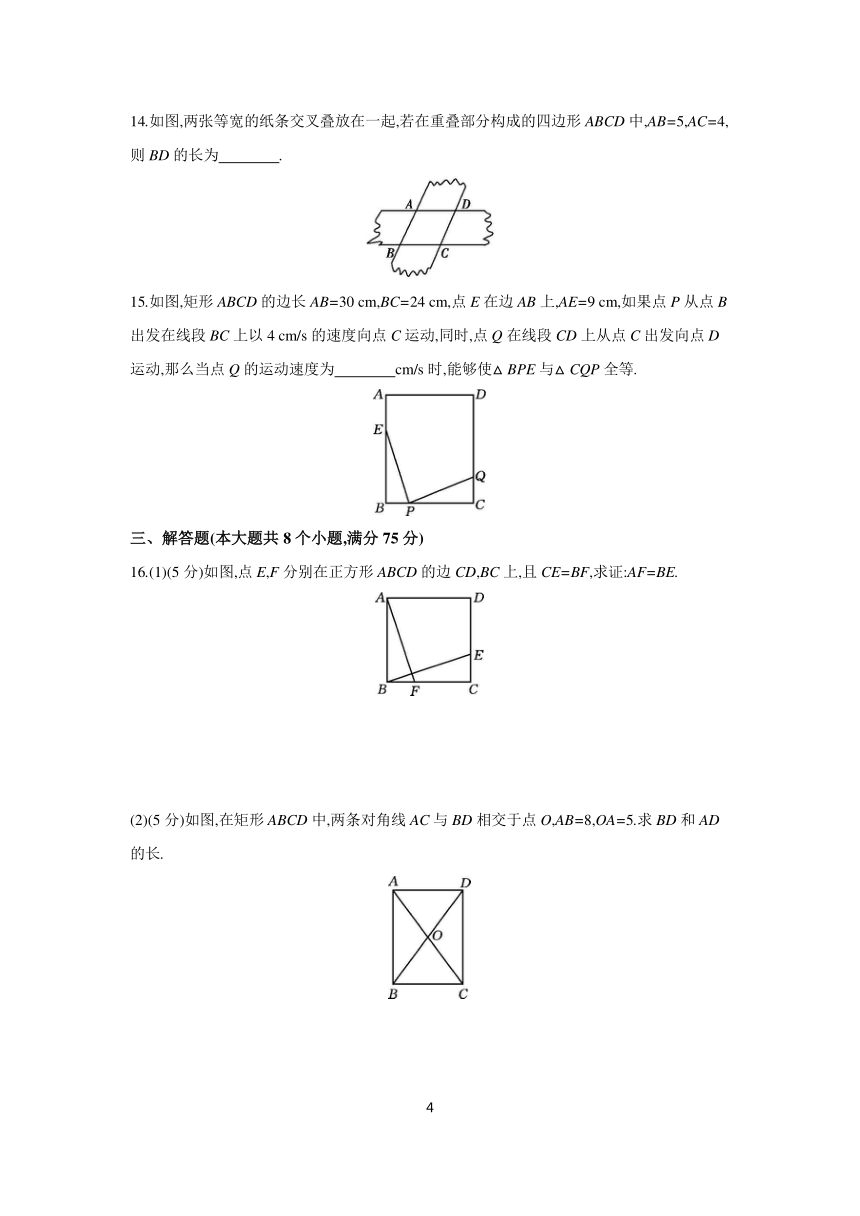
14.如图,两张等宽的纸条交叉叠放在一起,若在重叠部分构成的四边形ABCD中,AB=5,AC=4,则BD的长为 .
15.如图,矩形ABCD的边长AB=30 cm,BC=24 cm,点E在边AB上,AE=9 cm,如果点P从点B出发在线段BC上以4 cm/s的速度向点C运动,同时,点Q在线段CD上从点C出发向点D运动,那么当点Q的运动速度为 cm/s时,能够使△BPE与△CQP全等.
三、解答题(本大题共8个小题,满分75分)
16.(1)(5分)如图,点E,F分别在正方形ABCD的边CD,BC上,且CE=BF,求证:AF=BE.
(2)(5分)如图,在矩形ABCD中,两条对角线AC与BD相交于点O,AB=8,OA=5.求BD和AD的长.
17.(9分)在平行四边形ABCD中,E为BC边上的一点,连接AE,BD,且∠ABE=∠EAD.
(1)求证:AB=AE.
(2)当∠ABE=2∠ADB时,求证:平行四边形ABCD是菱形.
18.(9分)如图,O是菱形ABCD的对角线的交点,DE∥AC,CE∥BD,DE,CE交于点E.
(1)求证:四边形OCED是矩形.
(2)若菱形ABCD的边长AB=2,∠BAD=120°,求DE+CE的长.
19.(9分)如图,在△ABC中,AB=AC,点D为边BC上一点,以AB,BD为邻边作 ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD.
(2)若BD=CD,求证:四边形ADCE是矩形.
20.(9分)如图,在平行四边形ABCD中,AB≠AC,连接AC,AE是∠BAD的平分线,交边DC的延长线于点F.
(1)证明:CE=CF.
(2)连接BF,若∠ABC=60°,BC=2AB,试判断四边形ABFC的形状,并说明理由.
21.(9分)如图,在矩形ABCD中,DE⊥AC于点E,BF⊥AC于点F.
(1)求证:四边形DEBF是平行四边形.
(2)如果AB∶AD=∶1,请求出四边形DEBF与矩形ABCD的面积之比.
22.(10分)如图,在等边三角形ABC中,BC=6 cm.射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,同时点F从点B出发沿射线BC以2 cm/s的速度运动,设两点的运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:四边形AFCE是平行四边形.
(2)填空:①当t为 s时,四边形ACFE是菱形.
②当t为 s时,△ACE的面积是△ACF的面积的2倍.
23.(10分)(1)如图1,矩形ABCD的对角线AC,BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,判断四边形CODP的形状,并说明理由.
(2)如图2,如果将(1)中的矩形变为菱形,(1)中的结论应变为什么 请说明理由.
(3)如图3,如果将(1)中的矩形变为正方形,(1)中的结论又应变为什么 请说明理由.
参考答案
1.C 2.C 3.D 4.A 5.A 6.A 7.B 8.C 9.C 10.D
11. 12.(5,0) 13. 14.2
15.4或7 提示:①当EB=PC,BP=QC时,△BPE≌△CQP.
∵AB=30 cm,AE=9 cm,
∴BE=21 cm,
∴PC=21 cm.
∵CB=24 cm,
∴BP=3 cm.
∵点P从点B出发在线段BC上以4 cm/s的速度向点C向运动,
∴时间为3÷4= s.
∴点Q的运动速度为3÷=4 cm/s.
②当BP=CP,BE=QC时,△BEP≌△CQP.
设x秒时,BP=CP,
由题意得4x=24-4x,
解得x=3,
∴21÷3=7 cm/s.
故答案为4或7.
16.(1)证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°. 2分
在△ABF与△BCE中,
∴△ABF≌△BCE(SAS),
∴AF=BE. 5分
(2)解:∵四边形ABCD是矩形,
∴AC=2OA=10,∠BAD=90°,
∴BD=AC=10, 3分
∴AD==6,
∴BD的长为10,AD的长为6. 5分
17.证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠EAD=∠AEB.
∵∠ABE=∠EAD,∴∠ABE=∠AEB,∴AB=AE. 4分
(2)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠ADB=∠DBC.
∵∠ABE=2∠ADB,∴∠ABE=2∠DBC,∴∠ABD=∠DBC=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形. 9分
18.解:(1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵O是菱形ABCD的对角线的交点,
∴∠COD=90°,∴四边形OCED是矩形. 4分
(2)在菱形ABCD中,∠BAD=120°,可知∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC=2,∴OC=1,DO=BO=,
由矩形OCED可知DE=OC=1,CE=OD=,∴DE+CE=+1. 9分
19.证明:(1)∵四边形ABDE是平行四边形,
∴AB∥DE,AB=DE,∴∠B=∠EDC.
又∵AB=AC,∴AC=DE,∠B=∠ACB,∴∠EDC=∠ACD.
∵在△ADC和△ECD中,∴△ADC≌△ECD(SAS). 4分
(2)∵四边形ABDE是平行四边形,
∴BD∥AE,BD=AE,∴AE∥CD.
又∵BD=CD,∴AE=CD,
∴四边形ADCE是平行四边形.
在△ABC中,AB=AC,BD=CD,∴AD⊥BC,
∴∠ADC=90°,∴四边形ADCE是矩形. 9分
20.解:(1)证明:∵AE是∠BAD的平分线,∴∠BAF=∠DAF.
∵四边形ABCD是平行四边形,∴AB∥DF,AD∥BC,
∴∠BAF=∠F,∠DAF=∠CEF,∴∠F=∠DAF=∠CEF,∴CE=CF. 3分
(2)四边形ABFC是矩形, 4分
理由:∵∠ABC=60°,AD∥BC,∴∠BAD=120°.
∵∠BAF=∠DAF,∴∠BAF=60°,则△ABE是等边三角形,
可得AB=BE=AE,∠BEA=∠AFC=60°.
∵BC=2AB,∴AE=BE=EC,∴∠EAC=∠ECA=30°,∴∠BAC=90°,
在△ABE和△FCE中,∵
∴△ABE≌△FCE(ASA),
∴AB=FC.
又∵AB∥FC,∴四边形ABFC是平行四边形,
再由∠BAC=90°,可知四边形ABFC是矩形. 9分
21.解:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=CB,
∴∠DAE=∠BCF.
∵BF⊥AC,DE⊥AC,
∴∠AED=∠CFB=90°,BF∥DE. 2分
在△ADE和△CBF中,
∴△ADE≌△CBF(AAS),
∴DE=BF.
又∵BF∥DE,
∴四边形DEBF是平行四边形. 4分
(2)设AD=x,则AB=x,AC==x.
∵DE⊥AC于点E,
∴DE===x. 6分
在△ADE中,AE==x,
同理CF=x,
∴EF=AC-AE-CF=x,
∴S四边形DEBF=EF·DE=x·x=x2.
∵S矩形ABCD=x·x=x2,
∴四边形DEBF与矩形ABCD的面积之比为1∶3. 9分
22.解:(1)∵AG∥BC,∴∠EAD=∠DCF,∠AED=∠DFC.
∵D为AC的中点,∴AD=CD.
在△ADE和△CDF中,
∴△ADE≌△CDF(AAS),∴DE=DF,
∴四边形AFCE是平行四边形. 4分
(2)①6. 6分
提示:若四边形ACFE是菱形,则有CF=AC=AE=6,则此时t=6÷1=6(s).
②2.4或4. 10分
提示:∵AG∥BC,∴△ACE和△ACF等高.∵△ACE的面积是△ACF的面积的2倍,
∴AE=2CF.
当点F在点C的左侧时,由t=2(6-2t),解得t=2.4;
当点F在点C的右侧时,由t=2(2t-6),解得t=4.
综上,当t=2.4或4时,△ACE的面积是△ACF的面积的2倍.
23.解:(1)四边形CODP的形状是菱形. 1分
理由如下:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=AC,OB=OD=BD,
∴OC=OD.
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形.
∵OC=OD,
∴四边形CODP是菱形. 3分
(2)四边形CODP的形状是矩形. 4分
理由如下:∵四边形ABCD是菱形,
∴AC⊥BD,∴∠DOC=90°.
∵DP∥OC,DP=OC,∴四边形CODP是平行四边形.
∵∠DOC=90°,∴平行四边形CODP是矩形. 6分
(3)四边形CODP的形状是正方形. 7分
理由如下:∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,OA=OC=AC,OB=OD=BD,
∴∠DOC=90°,OD=OC.
∵DP∥OC,DP=OC,∴四边形CODP是平行四边形.
∵∠DOC=90°,OD=OC,∴四边形CODP是正方形. 10分
2
(时间:100分钟 分值:120分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,请把正确答案的代号填入题后括号内.
1.若菱形的一条边长为1,则该菱形的周长为 ( )
A.2 B.3 C.4 D.6
2.在图中所示的 ABCD中,再添加下列某一个条件,不能判定 ABCD是矩形的是 ( )
A.AC=BD
B.AB⊥BC
C.∠1=∠2
D.∠ABC=∠BCD
3.如图,在正方形ABCD中,在BA延长线上取一点E,使BE=BD,连接DE,则∠EDA的度数为 ( )
A.10°
B.15°
C.30°
D.22.5°
4.如图,在正方形OABC中,点A的坐标是(-3,1),则点C的坐标是 ( )
A.(1,3) B.(2,3)
C.(3,2) D.(3,1)
5.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于 ( )
A. B.
C.12 D.24
6.如图,在△ABC中,AB
B.四边形CEDF为矩形
C.四边形CEDF为正方形
D.CD=BD
7.如图,在△ABC中,AD是∠BAC的平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,若AE=4 cm,则四边形AEDF的周长为 ( )
A.12 cm
B.16 cm
C.20 cm
D.22 cm
8.在 ABCD中,AB=6,BC=8,当 ABCD的面积最大时,下列结论不正确的是 ( )
A.AC=10 B.AC=BD
C.AC⊥BD D.∠A+∠C=180°
9.四边形ABCD的对角线AC和BD相交于点O,有下列条件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD;⑥正方形ABCD.则下列推理不成立的是 ( )
A.①④ ⑥ B.①③ ⑤
C.①② ⑥ D.②③ ④
10.如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD,BD,有下列结论:①AD=BC;②BD,AC互相平分;③四边形ACED是菱形;④BD⊥DE.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题3分,共15分)
11.正方形ABCD的对角线AC=2,则边长AB= .
12.如图,在平面直角坐标系中,菱形MNPO的顶点P的坐标是(3,4),则顶点M的坐标是 .
13.如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转到能与△CBP'重合,若PB=1,则PP'= .
14.如图,两张等宽的纸条交叉叠放在一起,若在重叠部分构成的四边形ABCD中,AB=5,AC=4,则BD的长为 .
15.如图,矩形ABCD的边长AB=30 cm,BC=24 cm,点E在边AB上,AE=9 cm,如果点P从点B出发在线段BC上以4 cm/s的速度向点C运动,同时,点Q在线段CD上从点C出发向点D运动,那么当点Q的运动速度为 cm/s时,能够使△BPE与△CQP全等.
三、解答题(本大题共8个小题,满分75分)
16.(1)(5分)如图,点E,F分别在正方形ABCD的边CD,BC上,且CE=BF,求证:AF=BE.
(2)(5分)如图,在矩形ABCD中,两条对角线AC与BD相交于点O,AB=8,OA=5.求BD和AD的长.
17.(9分)在平行四边形ABCD中,E为BC边上的一点,连接AE,BD,且∠ABE=∠EAD.
(1)求证:AB=AE.
(2)当∠ABE=2∠ADB时,求证:平行四边形ABCD是菱形.
18.(9分)如图,O是菱形ABCD的对角线的交点,DE∥AC,CE∥BD,DE,CE交于点E.
(1)求证:四边形OCED是矩形.
(2)若菱形ABCD的边长AB=2,∠BAD=120°,求DE+CE的长.
19.(9分)如图,在△ABC中,AB=AC,点D为边BC上一点,以AB,BD为邻边作 ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD.
(2)若BD=CD,求证:四边形ADCE是矩形.
20.(9分)如图,在平行四边形ABCD中,AB≠AC,连接AC,AE是∠BAD的平分线,交边DC的延长线于点F.
(1)证明:CE=CF.
(2)连接BF,若∠ABC=60°,BC=2AB,试判断四边形ABFC的形状,并说明理由.
21.(9分)如图,在矩形ABCD中,DE⊥AC于点E,BF⊥AC于点F.
(1)求证:四边形DEBF是平行四边形.
(2)如果AB∶AD=∶1,请求出四边形DEBF与矩形ABCD的面积之比.
22.(10分)如图,在等边三角形ABC中,BC=6 cm.射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动,同时点F从点B出发沿射线BC以2 cm/s的速度运动,设两点的运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:四边形AFCE是平行四边形.
(2)填空:①当t为 s时,四边形ACFE是菱形.
②当t为 s时,△ACE的面积是△ACF的面积的2倍.
23.(10分)(1)如图1,矩形ABCD的对角线AC,BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,判断四边形CODP的形状,并说明理由.
(2)如图2,如果将(1)中的矩形变为菱形,(1)中的结论应变为什么 请说明理由.
(3)如图3,如果将(1)中的矩形变为正方形,(1)中的结论又应变为什么 请说明理由.
参考答案
1.C 2.C 3.D 4.A 5.A 6.A 7.B 8.C 9.C 10.D
11. 12.(5,0) 13. 14.2
15.4或7 提示:①当EB=PC,BP=QC时,△BPE≌△CQP.
∵AB=30 cm,AE=9 cm,
∴BE=21 cm,
∴PC=21 cm.
∵CB=24 cm,
∴BP=3 cm.
∵点P从点B出发在线段BC上以4 cm/s的速度向点C向运动,
∴时间为3÷4= s.
∴点Q的运动速度为3÷=4 cm/s.
②当BP=CP,BE=QC时,△BEP≌△CQP.
设x秒时,BP=CP,
由题意得4x=24-4x,
解得x=3,
∴21÷3=7 cm/s.
故答案为4或7.
16.(1)证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°. 2分
在△ABF与△BCE中,
∴△ABF≌△BCE(SAS),
∴AF=BE. 5分
(2)解:∵四边形ABCD是矩形,
∴AC=2OA=10,∠BAD=90°,
∴BD=AC=10, 3分
∴AD==6,
∴BD的长为10,AD的长为6. 5分
17.证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠EAD=∠AEB.
∵∠ABE=∠EAD,∴∠ABE=∠AEB,∴AB=AE. 4分
(2)∵四边形ABCD是平行四边形,∴AD∥BC,∴∠ADB=∠DBC.
∵∠ABE=2∠ADB,∴∠ABE=2∠DBC,∴∠ABD=∠DBC=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形. 9分
18.解:(1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵O是菱形ABCD的对角线的交点,
∴∠COD=90°,∴四边形OCED是矩形. 4分
(2)在菱形ABCD中,∠BAD=120°,可知∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC=2,∴OC=1,DO=BO=,
由矩形OCED可知DE=OC=1,CE=OD=,∴DE+CE=+1. 9分
19.证明:(1)∵四边形ABDE是平行四边形,
∴AB∥DE,AB=DE,∴∠B=∠EDC.
又∵AB=AC,∴AC=DE,∠B=∠ACB,∴∠EDC=∠ACD.
∵在△ADC和△ECD中,∴△ADC≌△ECD(SAS). 4分
(2)∵四边形ABDE是平行四边形,
∴BD∥AE,BD=AE,∴AE∥CD.
又∵BD=CD,∴AE=CD,
∴四边形ADCE是平行四边形.
在△ABC中,AB=AC,BD=CD,∴AD⊥BC,
∴∠ADC=90°,∴四边形ADCE是矩形. 9分
20.解:(1)证明:∵AE是∠BAD的平分线,∴∠BAF=∠DAF.
∵四边形ABCD是平行四边形,∴AB∥DF,AD∥BC,
∴∠BAF=∠F,∠DAF=∠CEF,∴∠F=∠DAF=∠CEF,∴CE=CF. 3分
(2)四边形ABFC是矩形, 4分
理由:∵∠ABC=60°,AD∥BC,∴∠BAD=120°.
∵∠BAF=∠DAF,∴∠BAF=60°,则△ABE是等边三角形,
可得AB=BE=AE,∠BEA=∠AFC=60°.
∵BC=2AB,∴AE=BE=EC,∴∠EAC=∠ECA=30°,∴∠BAC=90°,
在△ABE和△FCE中,∵
∴△ABE≌△FCE(ASA),
∴AB=FC.
又∵AB∥FC,∴四边形ABFC是平行四边形,
再由∠BAC=90°,可知四边形ABFC是矩形. 9分
21.解:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=CB,
∴∠DAE=∠BCF.
∵BF⊥AC,DE⊥AC,
∴∠AED=∠CFB=90°,BF∥DE. 2分
在△ADE和△CBF中,
∴△ADE≌△CBF(AAS),
∴DE=BF.
又∵BF∥DE,
∴四边形DEBF是平行四边形. 4分
(2)设AD=x,则AB=x,AC==x.
∵DE⊥AC于点E,
∴DE===x. 6分
在△ADE中,AE==x,
同理CF=x,
∴EF=AC-AE-CF=x,
∴S四边形DEBF=EF·DE=x·x=x2.
∵S矩形ABCD=x·x=x2,
∴四边形DEBF与矩形ABCD的面积之比为1∶3. 9分
22.解:(1)∵AG∥BC,∴∠EAD=∠DCF,∠AED=∠DFC.
∵D为AC的中点,∴AD=CD.
在△ADE和△CDF中,
∴△ADE≌△CDF(AAS),∴DE=DF,
∴四边形AFCE是平行四边形. 4分
(2)①6. 6分
提示:若四边形ACFE是菱形,则有CF=AC=AE=6,则此时t=6÷1=6(s).
②2.4或4. 10分
提示:∵AG∥BC,∴△ACE和△ACF等高.∵△ACE的面积是△ACF的面积的2倍,
∴AE=2CF.
当点F在点C的左侧时,由t=2(6-2t),解得t=2.4;
当点F在点C的右侧时,由t=2(2t-6),解得t=4.
综上,当t=2.4或4时,△ACE的面积是△ACF的面积的2倍.
23.解:(1)四边形CODP的形状是菱形. 1分
理由如下:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=AC,OB=OD=BD,
∴OC=OD.
∵DP∥OC,DP=OC,
∴四边形CODP是平行四边形.
∵OC=OD,
∴四边形CODP是菱形. 3分
(2)四边形CODP的形状是矩形. 4分
理由如下:∵四边形ABCD是菱形,
∴AC⊥BD,∴∠DOC=90°.
∵DP∥OC,DP=OC,∴四边形CODP是平行四边形.
∵∠DOC=90°,∴平行四边形CODP是矩形. 6分
(3)四边形CODP的形状是正方形. 7分
理由如下:∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,OA=OC=AC,OB=OD=BD,
∴∠DOC=90°,OD=OC.
∵DP∥OC,DP=OC,∴四边形CODP是平行四边形.
∵∠DOC=90°,OD=OC,∴四边形CODP是正方形. 10分
2
