2023-2024学年初中数学华东师大版七年级下册第7章 一次方程组 单元练习(含答案)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版七年级下册第7章 一次方程组 单元练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 124.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 06:52:54 | ||
图片预览



文档简介
第7章 一次方程组
(时间:100分钟 分值:120分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,将正确答案的代号填入题后括号内.
1.下列各方程中,是二元一次方程的是 ( )
A.xy+x=0 B.x+1=3x
C.x-y=0 D.x+y+z=0
2.已知是二元一次方程2x-y=6的解,则k的值为 ( )
A.2 B.-2 C.3 D.-3
3.已知关于x,y的二元一次方程组的解是则a+b的值为 ( )
A.2 B.3 C.4 D.5
4.用代入法解方程组比较合理的变形是 ( )
A.由①得x= B.由①得y=
C.由②得x= D.由②得y=2x-11
5.利用加减消元法解方程组下列做法正确的是 ( )
A.要消去y,可将①×3-②
B.要消去x,可将①×5+②×8
C.要消去y,可将①×5+②×8
D.要消去x,可将①-②×3
6.为了绿化校园,七年级(2)班的40名学生共种树96棵,已知男生每人种3棵,女生每人种2棵,设该班男生有x人,女生有y人,根据题意,所列方程组正确的是 ( )
A. B.
C. D.
7.已知方程组若将①×m+②×n可以得到3x+y的值,则m,n的值可以是 ( )
A.m=1,n=1 B.m=2,n=0
C.m=-1,n=3 D.m=3,n=-1
8.小明、小亮、小颖玩飞镖游戏,他们每人投靶5次,中靶情况如图所示.规定投中同一圆环的得分相同.若小明的得分为21分,小亮的得分为17分,则小颖的得分为 ( )
A.19分 B.20分 C.21分 D.22分
9.一个班级,若分成12个小组,则余3人,若每组增加2人,则可分成8组,仍余3人,这个班的人数是 ( )
A.39 B.43 C.51 D.59
10.某服装厂要生产一批某种型号的学生服装,已知3米长的布料可做上衣2件或裤子3条,1件上衣与1条裤子为1套,现计划用1200米长的这种布料生产,那么共能生产这种服装 ( )
A.480套 B.500套 C.520套 D.540套
二、填空题(每小题3分,共15分)
11.笼中有x只鸡,y只兔,共有36只脚,则根据题意列出的方程为 .
12.由方程组可得y与x之间的关系是 .
13.二元一次方程3x+2y=15共有 组正整数解.
14.我国古典数学文献《增删算法统宗·六均输》中有这样一道题:甲、乙两人一同放牧,两人暗地里在数羊的数量,如果乙给甲9只羊,则甲的羊数量为乙的两倍;如果甲给乙9只羊,则两人的羊数量相同.故甲的羊数量为 .
15.如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边上的两端点上的数加起来,将和写在这条边上,已知AB边上的数为3,BC边上的数为7,CD边上的数为12,则AD边上的数为 .
三、解答题(本大题共8个小题,满分75分)
16.解方程组:
(1)(5分) (2)(5分)
17.(9分)解方程组:
18.(9分)如图,在大长方形中放入6个形状、大小相同的小长方形,所标尺寸如图所示,求图中大长方形的面积.
19.(9分)小华和小明共同解方程组解完后小华与小明在交流时,有下面一段话:
根据小华和小明两位同学的对话,解答下列问题:
(1)求(a+b)2023的值.
(2)若是二元一次方程kx+(k-2)y=2k+3的解,求k的值.
20.(9分)课堂上,老师出了一道题:解方程组小梁提供了如下解法:设x+y=m,x-y=n,则原方程组可变为由①得2m+3n=36③,由③×2+②×3得13m=156,解得m=12,把m=12代入②,得n=4,于是可得方程组解得
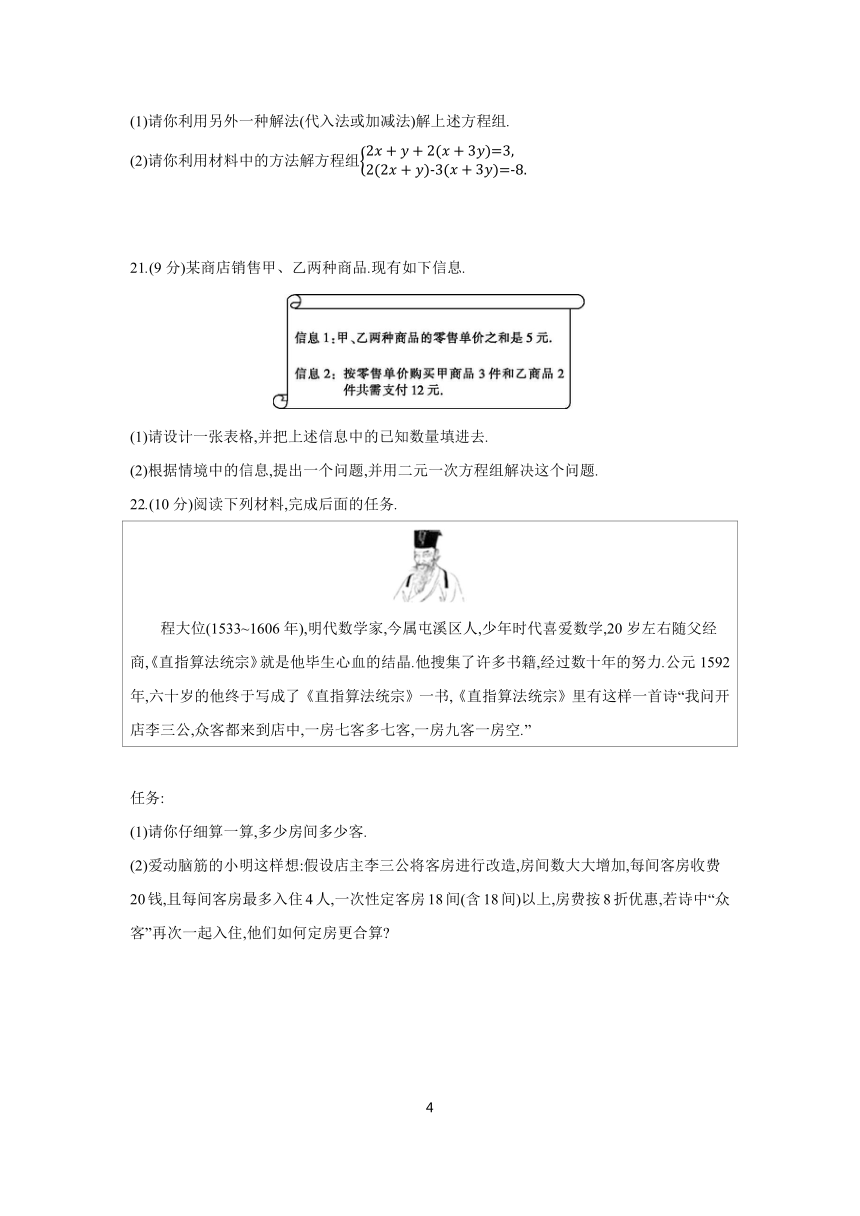
(1)请你利用另外一种解法(代入法或加减法)解上述方程组.
(2)请你利用材料中的方法解方程组
21.(9分)某商店销售甲、乙两种商品.现有如下信息.
(1)请设计一张表格,并把上述信息中的已知数量填进去.
(2)根据情境中的信息,提出一个问题,并用二元一次方程组解决这个问题.
22.(10分)阅读下列材料,完成后面的任务.
程大位(1533~1606年),明代数学家,今属屯溪区人,少年时代喜爱数学,20岁左右随父经商,《直指算法统宗》就是他毕生心血的结晶.他搜集了许多书籍,经过数十年的努力.公元1592年,六十岁的他终于写成了《直指算法统宗》一书,《直指算法统宗》里有这样一首诗“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”
任务:
(1)请你仔细算一算,多少房间多少客.
(2)爱动脑筋的小明这样想:假设店主李三公将客房进行改造,房间数大大增加,每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间(含18间)以上,房费按8折优惠,若诗中“众客”再次一起入住,他们如何定房更合算
23.(10分)向老师在为学校购买了语文阅读活动的书籍后,回学校向财务室董老师交账说:“我买了两种书共105本,单价分别为8元和12元,买书前我领了1500元,现在还余418元.”董老师算了一下,说:“你肯定搞错了.”
(1)董老师为什么说向老师弄错了 试用方程的知识给予解释.
(2)向老师连忙拿出购物发票,发现的确错了,因为他还买了一本笔记本,但笔记本的单价已模糊不清,只能辨认出应为小于5元的整数,笔记本的单价可能为多少元
参考答案
1.C 2.A 3.D 4.D 5.C 6.C 7.A 8.A 9.C 10.A
11.2x+4y=36 12.y-2x=3 13.2 14.63
15.8 提示:设点A表示的数为x,点D表示的数为y,则点B表示的数为3-x,点C表示的数为12-y,根据题意得3-x+12-y=7,解得x+y=8,∴AD边上的数是8.
16.(1)解:①+②得6a=-6,∴a=-1, 2分
将a=-1代入①,得-1+2b=3,∴b=2,∴原方程组的解为 5分
(2)解:②×4得28x+8y=64③,③-①得25x=50,∴x=2. 2分
将x=2代入①,得3×2+8y=14,∴y=1,∴原方程组的解为 5分
17.解:把③代入①,得5y+z=12④,
把③代入②,得6y+5z=22⑤,
④×5-⑤得19y=38,
解得y=2, 5分
把y=2代入④,得z=2,
把y=2,z=2代入①,得x+2+2=12,
解得x=8,
故原方程组的解为 9分
18.解:设小长方形的长为x cm,宽为y cm,
依题意得
解得 6分
∴小长方形的长为8 cm,宽为2 cm,
∴S大长方形=14×10=140 cm2. 9分
19.解:(1)把代入方程②,得7×(-3)+b=-27,解得b=-6. 2分
把代入方程①,得5a+2×4=33,解得a=5. 4分
把a=5,b=-6代入,得(a+b)2023=(5-6)2023=(-1)2023=-1. 6分
(2)将代入kx+(k-2)y=2k+3,得5k-6(k-2)=2k+3,
∴5k-6k+12=2k+3,解得k=3. 9分
20.解:(1)答案不唯一,用代入法:原方程组化简,得 2分
由①得y=5x-36③,将③代入②,得x+5(5x-36)=28,解得x=8, 3分
把x=8代入③,得y=4,∴原方程组的解为 5分
(2)设2x+y=m,x+3y=n,则原方程组变为 6分
①×2-②得7n=14,∴n=2,将n=2代入①,得m=-1. 7分
于是可得方程组③-④×2得-5y=-5,∴y=1,∴x=-1,∴原方程组的解为 9分
21.解:(1)可设计如下表格.
销售单价(元/件) 数量(件) 金额(元)
甲商品 3
乙商品 2
合计 5 12
4分
(2)答案不唯一.例如,
提问:甲、乙两种商品零售单价分别是多少元 6分
设甲商品零售单价为x元/件,乙商品零售单价为y元/件,
根据题意,得
解得
答:甲商品零售单价为2元/件,乙商品零售单价为3元/件. 9分
22.解:(1)设该店有客房x间,房客y人,
根据题意得 3分
解得
答:该店有客房8间,房客63人. 5分
(2)若每间客房住4人,则63名客人至少需要客房16间,需要付费16×20=320钱;
若一次性定客房18间,则需付费18×20×0.8=288钱, 8分
288<320,故选择一次性定客房18间更合算.
答:若诗中“众客”再次一起入住,则选择一次性定客房18间更合算. 10分
23.解:(1)设单价为8元的书买了x本,单价为12元的书买了y本,
根据题意可得方程组 2分
解得
显然书的本数应为整数,不能为小数,不符合题意,
故一定是向老师弄错了. 5分
(2)设笔记本的单价为a元,
根据题意可列方程组为 7分
解得y=,
要使y为整数,则a必为偶数,又因为a是小于5的整数,
所以当a=2时,y=60符合题意,
答:笔记本的价格可能是2元. 10分
2
(时间:100分钟 分值:120分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,将正确答案的代号填入题后括号内.
1.下列各方程中,是二元一次方程的是 ( )
A.xy+x=0 B.x+1=3x
C.x-y=0 D.x+y+z=0
2.已知是二元一次方程2x-y=6的解,则k的值为 ( )
A.2 B.-2 C.3 D.-3
3.已知关于x,y的二元一次方程组的解是则a+b的值为 ( )
A.2 B.3 C.4 D.5
4.用代入法解方程组比较合理的变形是 ( )
A.由①得x= B.由①得y=
C.由②得x= D.由②得y=2x-11
5.利用加减消元法解方程组下列做法正确的是 ( )
A.要消去y,可将①×3-②
B.要消去x,可将①×5+②×8
C.要消去y,可将①×5+②×8
D.要消去x,可将①-②×3
6.为了绿化校园,七年级(2)班的40名学生共种树96棵,已知男生每人种3棵,女生每人种2棵,设该班男生有x人,女生有y人,根据题意,所列方程组正确的是 ( )
A. B.
C. D.
7.已知方程组若将①×m+②×n可以得到3x+y的值,则m,n的值可以是 ( )
A.m=1,n=1 B.m=2,n=0
C.m=-1,n=3 D.m=3,n=-1
8.小明、小亮、小颖玩飞镖游戏,他们每人投靶5次,中靶情况如图所示.规定投中同一圆环的得分相同.若小明的得分为21分,小亮的得分为17分,则小颖的得分为 ( )
A.19分 B.20分 C.21分 D.22分
9.一个班级,若分成12个小组,则余3人,若每组增加2人,则可分成8组,仍余3人,这个班的人数是 ( )
A.39 B.43 C.51 D.59
10.某服装厂要生产一批某种型号的学生服装,已知3米长的布料可做上衣2件或裤子3条,1件上衣与1条裤子为1套,现计划用1200米长的这种布料生产,那么共能生产这种服装 ( )
A.480套 B.500套 C.520套 D.540套
二、填空题(每小题3分,共15分)
11.笼中有x只鸡,y只兔,共有36只脚,则根据题意列出的方程为 .
12.由方程组可得y与x之间的关系是 .
13.二元一次方程3x+2y=15共有 组正整数解.
14.我国古典数学文献《增删算法统宗·六均输》中有这样一道题:甲、乙两人一同放牧,两人暗地里在数羊的数量,如果乙给甲9只羊,则甲的羊数量为乙的两倍;如果甲给乙9只羊,则两人的羊数量相同.故甲的羊数量为 .
15.如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边上的两端点上的数加起来,将和写在这条边上,已知AB边上的数为3,BC边上的数为7,CD边上的数为12,则AD边上的数为 .
三、解答题(本大题共8个小题,满分75分)
16.解方程组:
(1)(5分) (2)(5分)
17.(9分)解方程组:
18.(9分)如图,在大长方形中放入6个形状、大小相同的小长方形,所标尺寸如图所示,求图中大长方形的面积.
19.(9分)小华和小明共同解方程组解完后小华与小明在交流时,有下面一段话:
根据小华和小明两位同学的对话,解答下列问题:
(1)求(a+b)2023的值.
(2)若是二元一次方程kx+(k-2)y=2k+3的解,求k的值.
20.(9分)课堂上,老师出了一道题:解方程组小梁提供了如下解法:设x+y=m,x-y=n,则原方程组可变为由①得2m+3n=36③,由③×2+②×3得13m=156,解得m=12,把m=12代入②,得n=4,于是可得方程组解得
(1)请你利用另外一种解法(代入法或加减法)解上述方程组.
(2)请你利用材料中的方法解方程组
21.(9分)某商店销售甲、乙两种商品.现有如下信息.
(1)请设计一张表格,并把上述信息中的已知数量填进去.
(2)根据情境中的信息,提出一个问题,并用二元一次方程组解决这个问题.
22.(10分)阅读下列材料,完成后面的任务.
程大位(1533~1606年),明代数学家,今属屯溪区人,少年时代喜爱数学,20岁左右随父经商,《直指算法统宗》就是他毕生心血的结晶.他搜集了许多书籍,经过数十年的努力.公元1592年,六十岁的他终于写成了《直指算法统宗》一书,《直指算法统宗》里有这样一首诗“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”
任务:
(1)请你仔细算一算,多少房间多少客.
(2)爱动脑筋的小明这样想:假设店主李三公将客房进行改造,房间数大大增加,每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间(含18间)以上,房费按8折优惠,若诗中“众客”再次一起入住,他们如何定房更合算
23.(10分)向老师在为学校购买了语文阅读活动的书籍后,回学校向财务室董老师交账说:“我买了两种书共105本,单价分别为8元和12元,买书前我领了1500元,现在还余418元.”董老师算了一下,说:“你肯定搞错了.”
(1)董老师为什么说向老师弄错了 试用方程的知识给予解释.
(2)向老师连忙拿出购物发票,发现的确错了,因为他还买了一本笔记本,但笔记本的单价已模糊不清,只能辨认出应为小于5元的整数,笔记本的单价可能为多少元
参考答案
1.C 2.A 3.D 4.D 5.C 6.C 7.A 8.A 9.C 10.A
11.2x+4y=36 12.y-2x=3 13.2 14.63
15.8 提示:设点A表示的数为x,点D表示的数为y,则点B表示的数为3-x,点C表示的数为12-y,根据题意得3-x+12-y=7,解得x+y=8,∴AD边上的数是8.
16.(1)解:①+②得6a=-6,∴a=-1, 2分
将a=-1代入①,得-1+2b=3,∴b=2,∴原方程组的解为 5分
(2)解:②×4得28x+8y=64③,③-①得25x=50,∴x=2. 2分
将x=2代入①,得3×2+8y=14,∴y=1,∴原方程组的解为 5分
17.解:把③代入①,得5y+z=12④,
把③代入②,得6y+5z=22⑤,
④×5-⑤得19y=38,
解得y=2, 5分
把y=2代入④,得z=2,
把y=2,z=2代入①,得x+2+2=12,
解得x=8,
故原方程组的解为 9分
18.解:设小长方形的长为x cm,宽为y cm,
依题意得
解得 6分
∴小长方形的长为8 cm,宽为2 cm,
∴S大长方形=14×10=140 cm2. 9分
19.解:(1)把代入方程②,得7×(-3)+b=-27,解得b=-6. 2分
把代入方程①,得5a+2×4=33,解得a=5. 4分
把a=5,b=-6代入,得(a+b)2023=(5-6)2023=(-1)2023=-1. 6分
(2)将代入kx+(k-2)y=2k+3,得5k-6(k-2)=2k+3,
∴5k-6k+12=2k+3,解得k=3. 9分
20.解:(1)答案不唯一,用代入法:原方程组化简,得 2分
由①得y=5x-36③,将③代入②,得x+5(5x-36)=28,解得x=8, 3分
把x=8代入③,得y=4,∴原方程组的解为 5分
(2)设2x+y=m,x+3y=n,则原方程组变为 6分
①×2-②得7n=14,∴n=2,将n=2代入①,得m=-1. 7分
于是可得方程组③-④×2得-5y=-5,∴y=1,∴x=-1,∴原方程组的解为 9分
21.解:(1)可设计如下表格.
销售单价(元/件) 数量(件) 金额(元)
甲商品 3
乙商品 2
合计 5 12
4分
(2)答案不唯一.例如,
提问:甲、乙两种商品零售单价分别是多少元 6分
设甲商品零售单价为x元/件,乙商品零售单价为y元/件,
根据题意,得
解得
答:甲商品零售单价为2元/件,乙商品零售单价为3元/件. 9分
22.解:(1)设该店有客房x间,房客y人,
根据题意得 3分
解得
答:该店有客房8间,房客63人. 5分
(2)若每间客房住4人,则63名客人至少需要客房16间,需要付费16×20=320钱;
若一次性定客房18间,则需付费18×20×0.8=288钱, 8分
288<320,故选择一次性定客房18间更合算.
答:若诗中“众客”再次一起入住,则选择一次性定客房18间更合算. 10分
23.解:(1)设单价为8元的书买了x本,单价为12元的书买了y本,
根据题意可得方程组 2分
解得
显然书的本数应为整数,不能为小数,不符合题意,
故一定是向老师弄错了. 5分
(2)设笔记本的单价为a元,
根据题意可列方程组为 7分
解得y=,
要使y为整数,则a必为偶数,又因为a是小于5的整数,
所以当a=2时,y=60符合题意,
答:笔记本的价格可能是2元. 10分
2
