2023-2024学年初中数学华东师大版七年级下册第9章 多边形 单元练习(含答案)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版七年级下册第9章 多边形 单元练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 167.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 06:53:49 | ||
图片预览




文档简介
第9章 多边形
(时间:100分钟 分值:120分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,将正确答案的代号填入题后括号内.
1.下列图形中,不具有稳定性的是 ( )
A.锐角三角形 B.长方形
C.直角三角形 D.等腰三角形
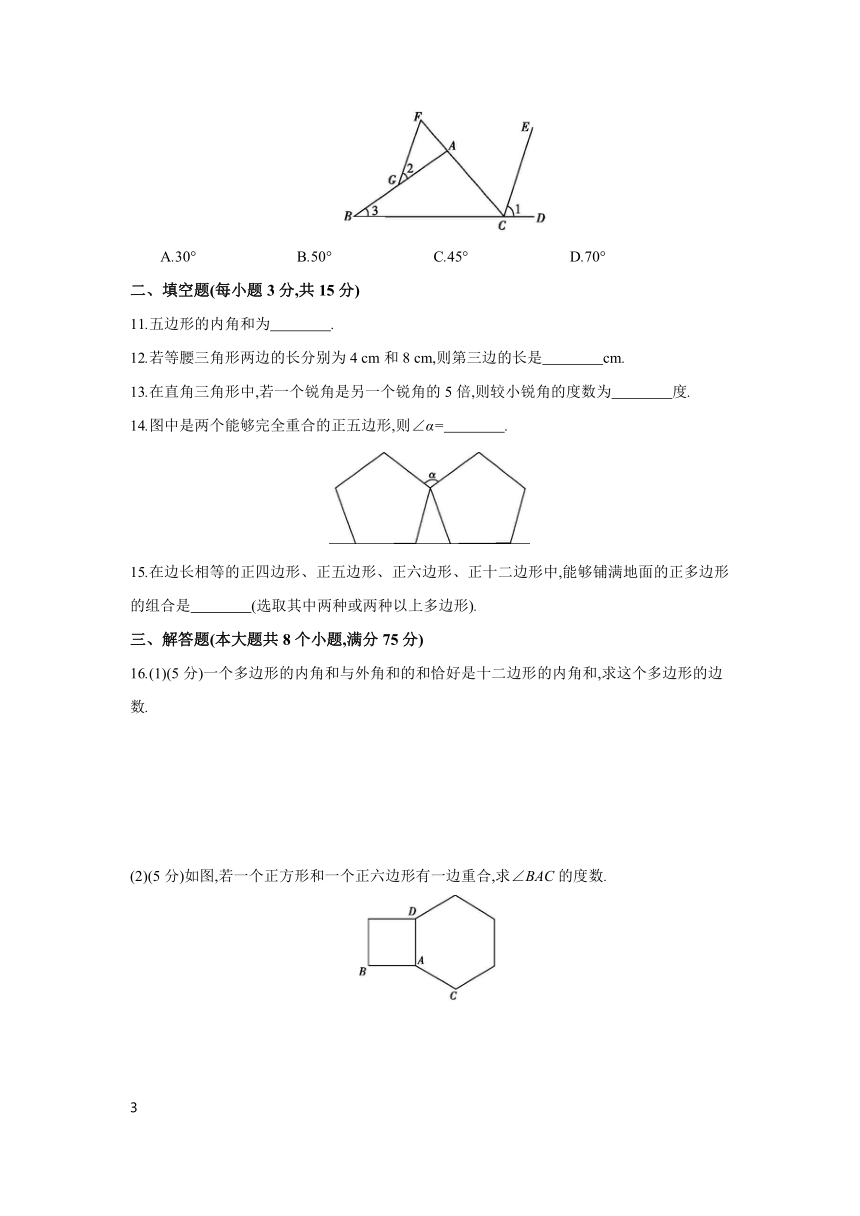
2.如图,以AB为边的三角形共有 ( )
A.5个 B.4个
C.3个 D.2个
3.以下列各组线段为边,能组成三角形的是 ( )
A.2 cm,5 cm,8 cm B.4 cm,4 cm,8 cm
C.3 cm,4 cm,5 cm D.1 cm,2 cm,3 cm
4.一个多边形每一个外角都等于18°,则这个多边形的边数为 ( )
A.20 B.16 C.12 D.10
5.下列四个图形中,线段AD是△ABC的高的是 ( )
A B
C D
6.如图,AD是△ABC的中线,则下列结论一定正确的是 ( )
A.AD⊥BC
B.∠BAD=∠CAD
C.AB=AC
D.BD=CD
7.如图,在五边形ABCDE中,AE∥CD.若∠A=∠C=110°,则∠B的大小为 ( )
A.70°
B.110°
C.140°
D.150°
8.当多边形每增加一条边时,它的 ( )
A.外角和与内角和都增加180°
B.外角和不变,内角和增加360°
C.外角和增加180°,内角和不变
D.外角和不变,内角和增加180°
9.如图,在△ABC中,AE是∠BAC的平分线,AD是BC边上的高线,且∠B=50°,∠C=60°,则∠EAD的大小为 ( )
A.35° B.5° C.15° D.25°
10.如图,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG∥CE交AB于点G.若∠1=75°,∠2=25°,则∠3的大小为 ( )
A.30° B.50° C.45° D.70°
二、填空题(每小题3分,共15分)
11.五边形的内角和为 .
12.若等腰三角形两边的长分别为4 cm和8 cm,则第三边的长是 cm.
13.在直角三角形中,若一个锐角是另一个锐角的5倍,则较小锐角的度数为 度.
14.图中是两个能够完全重合的正五边形,则∠α= .
15.在边长相等的正四边形、正五边形、正六边形、正十二边形中,能够铺满地面的正多边形的组合是 (选取其中两种或两种以上多边形).
三、解答题(本大题共8个小题,满分75分)
16.(1)(5分)一个多边形的内角和与外角和的和恰好是十二边形的内角和,求这个多边形的边数.
(2)(5分)如图,若一个正方形和一个正六边形有一边重合,求∠BAC的度数.
17.(9分)如图,已知△ABC.
(1)画中线AD.
(2)画△ABD的高BE及△ACD的高CF.
18.(9分)如图,在四边形ABCD中,AB⊥BC,∠C=60°,且∠D-∠BAD=10°,求∠1的度数.
19.(9分)如图,在△ABC中,BD⊥AC,垂足为D,∠ABD=54°,∠DBC=18°,求∠A,∠C的度数.
20.(9分)已知a,b,c是△ABC的三边长,a=3,b=7,设△ABC的周长是x.
(1)直接写出c及x的取值范围.
(2)若x是小于20的偶数,求c的长.
21.(9分)小芳家在装修,她在建材市场选中了一种漂亮的正八边形的地砖,可建材市场的服务员告诉她,仅一种正八边形的地砖是不能密铺地面的,遂又向她推荐各种尺寸、形状、花色的其他地砖,供小芳搭配选用的有正方形的、正三角形的、等腰直角三角形的、正六边形的、正五边形的、五角星形状的等等.小芳顿时选花了眼,你能帮忙筛选一下吗
(1)小芳应选择哪一种形状的地砖与正八边形地砖搭配使用,并说明理由.
(2)如果小芳不选正八边形的地砖,她还可以有哪些选择 (列举2种即可)
22.(10分)在学习了三角形后,同学们对三角形的角平分线展开了研究.
自主探究:
如图1,在△ABC中,BD,CE分别是∠ABC,∠ACB的平分线,BD,CE交于点O,∠A=72°.
(1)若∠ACB=42°,求∠BOC的度数.
反思交流:
(2)当∠ACB的大小改变时,∠BOC的大小是否发生变化 为什么 请写出证明过程.
探索发现:
(3)如图2,△ABC的两条外角平分线交于点G,请直接写出∠BGC与∠A的数量关系.
23.(10分)如图,在Rt△ABC中,有一个动点P,从点C出发,沿着C→A→B→C的路线运动,点P的运动速度为每秒3个单位长度,设运动的时间为t秒,AC=24,BC=18,AB=30.
(1)若CP把△ABC分成面积相等的两部分,请求出此时t的值.
(2)当t=15时,CP把△ABC分成的两部分的面积之比是S△APC∶S△BPC= .
(3)试探究当△BPC的面积为36时,点P的运动时间.
参考答案
1.B 2.C 3.C 4.A 5.D 6.D 7.C 8.D 9.B 10.B
11.540° 12.8 13.15 14.108° 15.正四边形、正六边形、正十二边形
16.(1)解:设这个多边形的边数为n,
则(n-2)×180°+360°=(12-2)×180°, 2分
解得n=10.
答:这个多边形的边数为10. 5分
(2)解:∵正六边形的每个内角度数是=120°,
∴∠DAC=120°, 2分
∴∠BAC=360°-∠DAC-∠BAD,
∴∠BAC=360°-120°-90°=150°. 5分
17.解:(1)中线AD如图所示. 3分
(2)△ABD的高BE及△ACD的高CF如图所示. 9分
18.解:∵AB⊥BC,
∴∠B=90°.
∵∠C=60°,
∴∠D+∠BAD=360°-90°-60°=210°. 4分
∵∠D-∠BAD=10°,
∴∠BAD=(210°-10°)÷2=100°,
∴∠1=180°-100°=80°. 9分
19.解:∵在△ABC中,BD⊥AC,
∴∠BDA=90°.
∵∠ABD=54°,
∴∠A=∠BDA-∠ABD=90°-54°=36°. 4分
∵∠ABD=54°,∠DBC=18°,
∴∠ABC=72°, 6分
∴∠C=180°-∠A-∠ABC=72°,
即∠A=36°,∠C=72°. 9分
20.解:(1)因为a=3,b=7,
所以4故x的取值范围为14(2)因为x为小于20的偶数,
所以x=18或x=16.
当x=18时,c=8;
当x=16时,c=6. 9分
21.解:(1)根据密铺的条件可知,小芳应从正方形和等腰直角三角形的地砖中选择. 2分
理由:①正方形、正八边形的内角分别为90°、135°,由于135°×2+90°=360°,故能密铺; 4分
②等腰直角三角形的一个内角为45°,正八边形的内角为135°,由于135°×2+45°×2=360°,故能密铺. 6分
故可以选择正方形和等腰直角三角形的地砖. 7分
(2)如果小芳不选正八边形的地砖,那么可以直接选择正方形或正三角形的地砖密铺地面,也可以将正方形地砖和正三角形地砖组合或者利用正六边形地砖和正三角形地砖组合密铺地面. 9分
22.解:(1)∵在△ABC中,∠A=72°,∠ACB=42°,
∴∠ABC=180°-∠A-∠ACB=66°. 1分
∵BD,CE分别是∠ABC,∠ACB的平分线,
∴∠OBC=∠ABC=33°,∠OCB=∠ACB=21°, 2分
∴∠BOC=180°-∠OBC-∠OCB=126°. 3分
(2)∠BOC的大小不发生变化. 4分
∵BD,CE分别是∠ABC,∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB, 5分
∴∠BOC=180°-∠OBC-∠OCB
=180°-(∠ABC+∠ACB)
=180°-(180°-∠A)
=90°+∠A
=126°, 7分
∴∠BOC的大小只与∠A的大小相关,与∠ACB的大小无关. 8分
(3)∠BGC=90°-∠A. 10分
23.解:(1)当P是AB的中点时,CP把△ABC分成面积相等的两部分,此时CA+AP=24+15=39, 1分
∴3t=39,解得t=13. 3分
(2)7∶3. 6分
提示:15×3=45,
AP=45-24=21,
图1
BP=30-21=9,
则S△APC∶S△BPC=21∶9=7∶3.
(3)分两种情况:
①如图1,当点P在AC上时,
∵△BCP的面积=36,
∴×18×CP=36,
图2
∴CP=4,
∴3t=4,∴t=; 8分
②如图2,当点P在AB上时,
hPB=hAB===.
∵S△BPC=36=·PB·hPB=PB×,
∴PB=5,
∴3t=24+30-5=49,解得t=.
综上所述,当S△BPC=36时,点P的运动时间为秒或秒. 10分
2
(时间:100分钟 分值:120分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,将正确答案的代号填入题后括号内.
1.下列图形中,不具有稳定性的是 ( )
A.锐角三角形 B.长方形
C.直角三角形 D.等腰三角形
2.如图,以AB为边的三角形共有 ( )
A.5个 B.4个
C.3个 D.2个
3.以下列各组线段为边,能组成三角形的是 ( )
A.2 cm,5 cm,8 cm B.4 cm,4 cm,8 cm
C.3 cm,4 cm,5 cm D.1 cm,2 cm,3 cm
4.一个多边形每一个外角都等于18°,则这个多边形的边数为 ( )
A.20 B.16 C.12 D.10
5.下列四个图形中,线段AD是△ABC的高的是 ( )
A B
C D
6.如图,AD是△ABC的中线,则下列结论一定正确的是 ( )
A.AD⊥BC
B.∠BAD=∠CAD
C.AB=AC
D.BD=CD
7.如图,在五边形ABCDE中,AE∥CD.若∠A=∠C=110°,则∠B的大小为 ( )
A.70°
B.110°
C.140°
D.150°
8.当多边形每增加一条边时,它的 ( )
A.外角和与内角和都增加180°
B.外角和不变,内角和增加360°
C.外角和增加180°,内角和不变
D.外角和不变,内角和增加180°
9.如图,在△ABC中,AE是∠BAC的平分线,AD是BC边上的高线,且∠B=50°,∠C=60°,则∠EAD的大小为 ( )
A.35° B.5° C.15° D.25°
10.如图,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG∥CE交AB于点G.若∠1=75°,∠2=25°,则∠3的大小为 ( )
A.30° B.50° C.45° D.70°
二、填空题(每小题3分,共15分)
11.五边形的内角和为 .
12.若等腰三角形两边的长分别为4 cm和8 cm,则第三边的长是 cm.
13.在直角三角形中,若一个锐角是另一个锐角的5倍,则较小锐角的度数为 度.
14.图中是两个能够完全重合的正五边形,则∠α= .
15.在边长相等的正四边形、正五边形、正六边形、正十二边形中,能够铺满地面的正多边形的组合是 (选取其中两种或两种以上多边形).
三、解答题(本大题共8个小题,满分75分)
16.(1)(5分)一个多边形的内角和与外角和的和恰好是十二边形的内角和,求这个多边形的边数.
(2)(5分)如图,若一个正方形和一个正六边形有一边重合,求∠BAC的度数.
17.(9分)如图,已知△ABC.
(1)画中线AD.
(2)画△ABD的高BE及△ACD的高CF.
18.(9分)如图,在四边形ABCD中,AB⊥BC,∠C=60°,且∠D-∠BAD=10°,求∠1的度数.
19.(9分)如图,在△ABC中,BD⊥AC,垂足为D,∠ABD=54°,∠DBC=18°,求∠A,∠C的度数.
20.(9分)已知a,b,c是△ABC的三边长,a=3,b=7,设△ABC的周长是x.
(1)直接写出c及x的取值范围.
(2)若x是小于20的偶数,求c的长.
21.(9分)小芳家在装修,她在建材市场选中了一种漂亮的正八边形的地砖,可建材市场的服务员告诉她,仅一种正八边形的地砖是不能密铺地面的,遂又向她推荐各种尺寸、形状、花色的其他地砖,供小芳搭配选用的有正方形的、正三角形的、等腰直角三角形的、正六边形的、正五边形的、五角星形状的等等.小芳顿时选花了眼,你能帮忙筛选一下吗
(1)小芳应选择哪一种形状的地砖与正八边形地砖搭配使用,并说明理由.
(2)如果小芳不选正八边形的地砖,她还可以有哪些选择 (列举2种即可)
22.(10分)在学习了三角形后,同学们对三角形的角平分线展开了研究.
自主探究:
如图1,在△ABC中,BD,CE分别是∠ABC,∠ACB的平分线,BD,CE交于点O,∠A=72°.
(1)若∠ACB=42°,求∠BOC的度数.
反思交流:
(2)当∠ACB的大小改变时,∠BOC的大小是否发生变化 为什么 请写出证明过程.
探索发现:
(3)如图2,△ABC的两条外角平分线交于点G,请直接写出∠BGC与∠A的数量关系.
23.(10分)如图,在Rt△ABC中,有一个动点P,从点C出发,沿着C→A→B→C的路线运动,点P的运动速度为每秒3个单位长度,设运动的时间为t秒,AC=24,BC=18,AB=30.
(1)若CP把△ABC分成面积相等的两部分,请求出此时t的值.
(2)当t=15时,CP把△ABC分成的两部分的面积之比是S△APC∶S△BPC= .
(3)试探究当△BPC的面积为36时,点P的运动时间.
参考答案
1.B 2.C 3.C 4.A 5.D 6.D 7.C 8.D 9.B 10.B
11.540° 12.8 13.15 14.108° 15.正四边形、正六边形、正十二边形
16.(1)解:设这个多边形的边数为n,
则(n-2)×180°+360°=(12-2)×180°, 2分
解得n=10.
答:这个多边形的边数为10. 5分
(2)解:∵正六边形的每个内角度数是=120°,
∴∠DAC=120°, 2分
∴∠BAC=360°-∠DAC-∠BAD,
∴∠BAC=360°-120°-90°=150°. 5分
17.解:(1)中线AD如图所示. 3分
(2)△ABD的高BE及△ACD的高CF如图所示. 9分
18.解:∵AB⊥BC,
∴∠B=90°.
∵∠C=60°,
∴∠D+∠BAD=360°-90°-60°=210°. 4分
∵∠D-∠BAD=10°,
∴∠BAD=(210°-10°)÷2=100°,
∴∠1=180°-100°=80°. 9分
19.解:∵在△ABC中,BD⊥AC,
∴∠BDA=90°.
∵∠ABD=54°,
∴∠A=∠BDA-∠ABD=90°-54°=36°. 4分
∵∠ABD=54°,∠DBC=18°,
∴∠ABC=72°, 6分
∴∠C=180°-∠A-∠ABC=72°,
即∠A=36°,∠C=72°. 9分
20.解:(1)因为a=3,b=7,
所以4
所以x=18或x=16.
当x=18时,c=8;
当x=16时,c=6. 9分
21.解:(1)根据密铺的条件可知,小芳应从正方形和等腰直角三角形的地砖中选择. 2分
理由:①正方形、正八边形的内角分别为90°、135°,由于135°×2+90°=360°,故能密铺; 4分
②等腰直角三角形的一个内角为45°,正八边形的内角为135°,由于135°×2+45°×2=360°,故能密铺. 6分
故可以选择正方形和等腰直角三角形的地砖. 7分
(2)如果小芳不选正八边形的地砖,那么可以直接选择正方形或正三角形的地砖密铺地面,也可以将正方形地砖和正三角形地砖组合或者利用正六边形地砖和正三角形地砖组合密铺地面. 9分
22.解:(1)∵在△ABC中,∠A=72°,∠ACB=42°,
∴∠ABC=180°-∠A-∠ACB=66°. 1分
∵BD,CE分别是∠ABC,∠ACB的平分线,
∴∠OBC=∠ABC=33°,∠OCB=∠ACB=21°, 2分
∴∠BOC=180°-∠OBC-∠OCB=126°. 3分
(2)∠BOC的大小不发生变化. 4分
∵BD,CE分别是∠ABC,∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB, 5分
∴∠BOC=180°-∠OBC-∠OCB
=180°-(∠ABC+∠ACB)
=180°-(180°-∠A)
=90°+∠A
=126°, 7分
∴∠BOC的大小只与∠A的大小相关,与∠ACB的大小无关. 8分
(3)∠BGC=90°-∠A. 10分
23.解:(1)当P是AB的中点时,CP把△ABC分成面积相等的两部分,此时CA+AP=24+15=39, 1分
∴3t=39,解得t=13. 3分
(2)7∶3. 6分
提示:15×3=45,
AP=45-24=21,
图1
BP=30-21=9,
则S△APC∶S△BPC=21∶9=7∶3.
(3)分两种情况:
①如图1,当点P在AC上时,
∵△BCP的面积=36,
∴×18×CP=36,
图2
∴CP=4,
∴3t=4,∴t=; 8分
②如图2,当点P在AB上时,
hPB=hAB===.
∵S△BPC=36=·PB·hPB=PB×,
∴PB=5,
∴3t=24+30-5=49,解得t=.
综上所述,当S△BPC=36时,点P的运动时间为秒或秒. 10分
2
