2023-2024学年初中数学华东师大版七年级下册第10章 轴对称、平移与旋转 单元练习(含答案)
文档属性
| 名称 | 2023-2024学年初中数学华东师大版七年级下册第10章 轴对称、平移与旋转 单元练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 405.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 06:54:36 | ||
图片预览



文档简介
第10章 轴对称、平移与旋转
(时间:100分钟 分值:120分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,将正确答案的代号填入题后括号内.
1.全等图形是指两个图形 ( )
A.大小相等 B.形状相同
C.完全重合 D.以上都不对
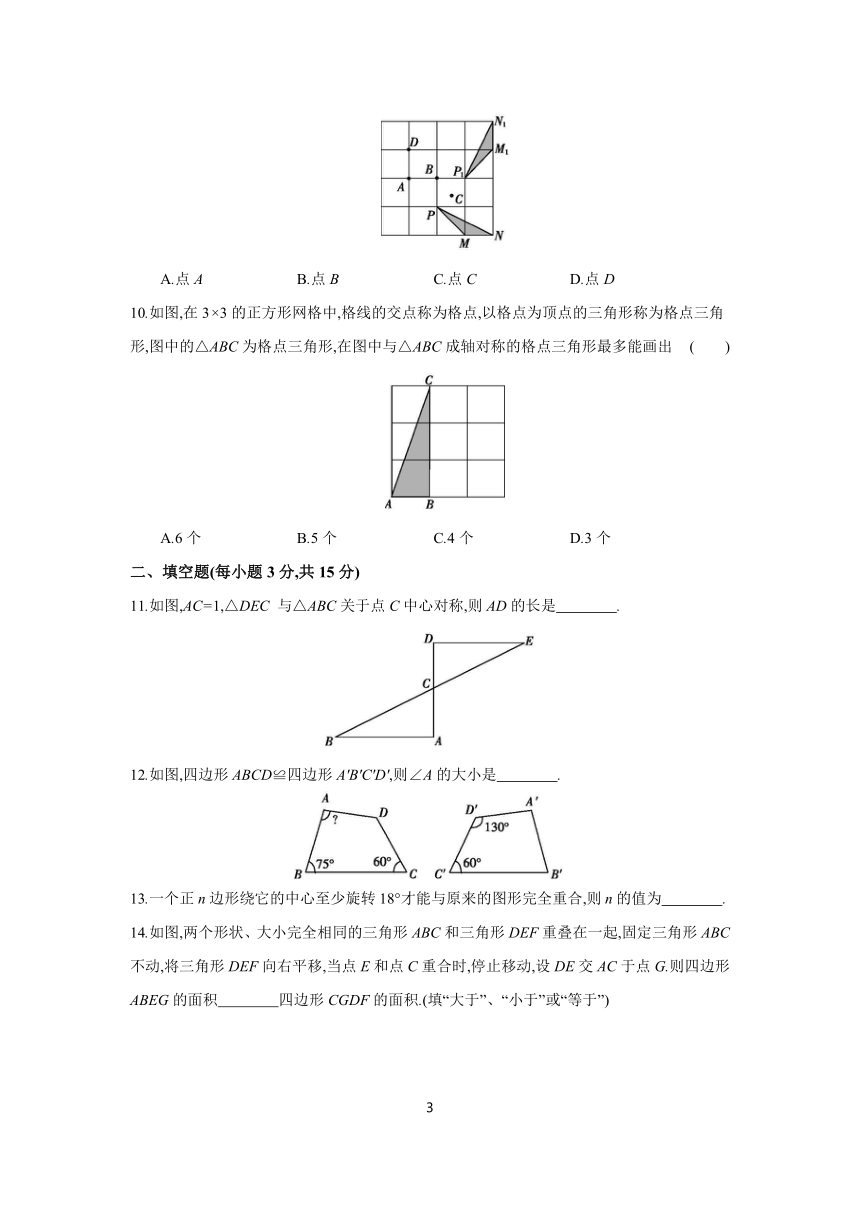
2.观察下列图案,能通过例图顺时针旋转90°得到的是 ( )
3.下列平移作图错误的是 ( )
4.下列图形既是轴对称图形又是中心对称图形的是 ( )
5.如图,△ABC≌△BAD,若AB=6 cm,AC=3 cm,BC=5 cm,则AD的长为 ( )
A.3 cm
B.5 cm
C.6 cm
D.以上都不对
6.如图,这是台球桌面示意图,阴影部分表示四个入球孔,小明按图中所示方向击球(球可以多次反弹),则球最后落入的球袋是 ( )
A.1号袋
B.2号袋
C.3号袋
D.4号袋
7.把图中的五角星图案绕着它的中心点O进行旋转,若五角星旋转后与自身重合,则至少需旋转 ( )
A.36°
B.45°
C.72°
D.90°
8.如图,将△ABC沿着由点B到点C的方向平移得到△DEF,已知BC=12,EC=8,那么平移的距离为 ( )
A.20 B.12 C.8 D.4
9.在如图所示的4×4的正方形网格中,△PMN绕某一点旋转一定的角度,得到△P1M1N1,其旋转中心是 ( )
A.点A B.点B C.点C D.点D
10.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中与△ABC成轴对称的格点三角形最多能画出 ( )
A.6个 B.5个 C.4个 D.3个
二、填空题(每小题3分,共15分)
11.如图,AC=1,△DEC 与△ABC关于点C中心对称,则AD的长是 .
12.如图,四边形ABCD≌四边形A'B'C'D',则∠A的大小是 .
13.一个正n边形绕它的中心至少旋转18°才能与原来的图形完全重合,则n的值为 .
14.如图,两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起,固定三角形ABC不动,将三角形DEF向右平移,当点E和点C重合时,停止移动,设DE交AC于点G.则四边形ABEG的面积 四边形CGDF的面积.(填“大于”、“小于”或“等于”)
15.一副直角三角尺如图1所示摆放,现将含45°角的三角尺ADE固定不动,将含30°角的三角尺ABC绕顶点A顺时针转动(旋转角不超过180度),使两块三角尺有一组边互相平行.如图2,当∠BAD=15°时,BC∥DE.当90°<∠BAD<180°时,所有符合条件的∠BAD的度数为 .
三、解答题(本大题共8个小题,满分75分)
16.(1)(5分)如图1,网格中的△ABC与△DEF成轴对称,请用所学轴对称的知识在网格中作出△ABC与△DEF的对称轴l.
(2)(5分)如图2,请在网格中作出△ABC关于直线MN成轴对称的△A'B'C'.
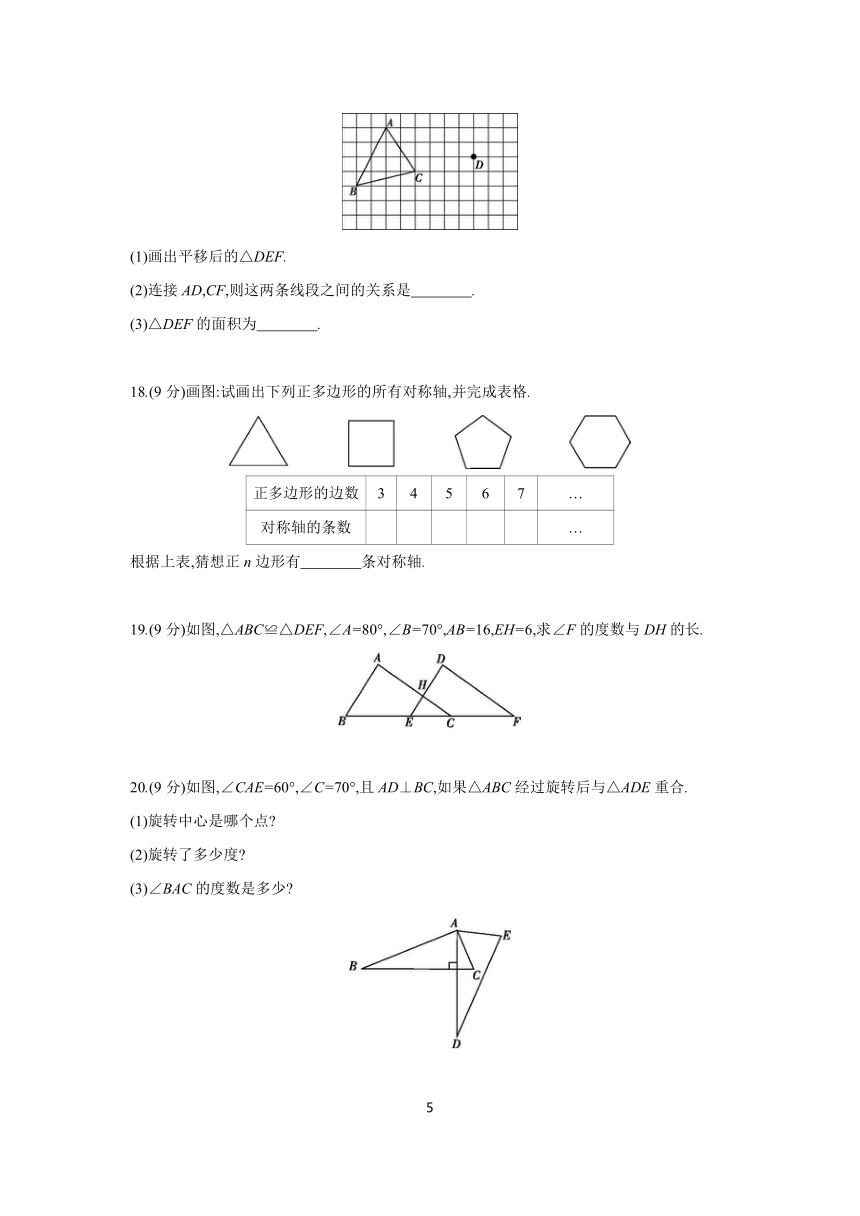
17.(9分)在如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,点A平移到点D的位置,点B,C平移后的对应点分别是点E,F.
(1)画出平移后的△DEF.
(2)连接AD,CF,则这两条线段之间的关系是 .
(3)△DEF的面积为 .
18.(9分)画图:试画出下列正多边形的所有对称轴,并完成表格.
正多边形的边数 3 4 5 6 7 …
对称轴的条数 …
根据上表,猜想正n边形有 条对称轴.
19.(9分)如图,△ABC≌△DEF,∠A=80°,∠B=70°,AB=16,EH=6,求∠F的度数与DH的长.
20.(9分)如图,∠CAE=60°,∠C=70°,且AD⊥BC,如果△ABC经过旋转后与△ADE重合.
(1)旋转中心是哪个点
(2)旋转了多少度
(3)∠BAC的度数是多少
21.(9分)图1、图2、图3是3×3的正方形网格,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影(请在图1、图2、图3中依次作答,均只需要画出符合条件的一种情形):
(1)在图1中选取1个空白小正方形涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
(2)在图2中选取1个空白小正方形涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)在图3中选取2个空白小正方形涂上阴影,使5个阴影小正方形组成一个轴对称图形.
22.(10分)如图,在锐角△ABC中,AC=7 cm,S△ABC=14 cm2,AD平分∠BAC,M,N分别是边AD,AB上的动点.
(1)求△ABC 的边AC上高的长度.
(2)求BM+MN的最小值.
23.(10分)在学习了全等图形的知识后,同学们结合以前学习的三角形三边之间的关系展开了探究活动.
问题情境:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
探究展示:
飞天组的分析过程如下:将△ACD绕点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断出中线AD的取值范围.
小明代表飞天组上台讲解:如图1,将△ACD绕着点D逆时针旋转180°得到△EBD.
∵AD是BC边上的中线,
∴BD=CD,(依据①)
由旋转的性质得△BDE≌△CDA,
∴BE=AC=6,(依据②)
在△ABE中,由三角形的三边关系得AB-BE∴10-6∴2合作交流:
(1)上述证明过程中的“依据①”和“依据②”分别是指:
依据①是 ;
依据②是 .
(2)对于这道题目,你还有不同的解法吗 若有,请写出来;若没有,请回答以下问题:解题时,条件中若出现“中点”“中线”字样时,应如何思考呢
(3)如图2,在 △ABC中,∠BAC=90°,AD是BC边上的中线,试作AC关于点D中心对称的BE;并求出∠ABE的度数.
参考答案
1.C 2.A 3.C 4.B 5.B 6.B 7.C 8.D 9.B 10.A
11.2 12.95° 13.20 14.等于
15.105°或135° 提示:如图,当AC∥DE时,∠BAD=∠DAE=45°;当BC∥AD时,∠DAB=∠B=60°;当BC∥AE时,∵∠EAB=∠B=60°,∴∠BAD=∠DAE+∠EAB=45°+60°=105°;当AB∥DE时,∵∠E=∠EAB=90°,∴∠BAD=∠DAE+∠EAB=45°+90°=135°.综上所述,当90°<∠BAD<180°时,∠BAD=105°或135°.
16.(1)解:如图1,直线l即为所作.
5分
(2)解:如图2,△A'B'C'即为所作.
5分
17.解:(1)如图,△DEF即为所求. 3分
(2)AD=CF,AD∥CF. 6分
(3)7. 9分
提示:S△DEF=×(2+4)×4-×2×3-×1×4=7.
18.解:作图如下,
3;4;5;6;7. 7分
n. 9分
19.解:∵∠A=80°,∠B=70°,
∴∠ACB=180°-∠A-∠B=30°. 2分
∵△ABC≌△DEF,AB=16,
∴∠F=∠ACB=30°,DE=AB=16. 6分
∵EH=6,
∴DH=16-6=10. 9分
20.解:(1)旋转中心是点A. 2分
(2)旋转的角度即为∠CAE=60°. 4分
(3)根据旋转的性质知,∠EAC=∠BAD=60°,∠C=∠E=70°. 5分
如图,设AD⊥BC于点F,
则∠AFB=90°,
∴在Rt△ABF中,∠B=90°-∠BAD=30°,
∴在△ABC中,∠BAC=180°-∠B-∠C=180°-30°-70°=80°. 9分
21.(1)如图1所示. 3分
(2)如图2所示.(答案不唯一) 6分
(3)如图3所示.(答案不唯一) 9分
22.解:(1)如图,作AC边上的高BE,垂足为E.
∵△ABC的面积是14 cm2,AC=7 cm,
∴×7×BE=14,
∴BE=4 cm. 4分
(2)如图,以AD为对称轴,作△ANM的对称图形,点N的对称点为点R.
∵AD平分∠CAB,△ABC为锐角三角形,
∴点R必在AC边上, 7分
∴MR=MN,
∴BM+MN=BM+MR,
∴BM+MN=BR≥BE,(垂线段最短)
∴BM+MN的最小值为4 cm. 10分
23.解:(1)依据①是中点的定义; 1分
依据②是全等三角形的对应边相等. 2分
(2)可以考虑构造以该中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中,从而解决问题. 5分
(3)如图,BE即为所求. 7分
易得△BDE≌△CDA,
∴∠E=∠CAD.
∵∠BAC=90°,
∴∠E+∠BAE=∠BAE+∠CAD=∠BAC=90°,
∴∠ABE=90°. 10分
2
(时间:100分钟 分值:120分)
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,将正确答案的代号填入题后括号内.
1.全等图形是指两个图形 ( )
A.大小相等 B.形状相同
C.完全重合 D.以上都不对
2.观察下列图案,能通过例图顺时针旋转90°得到的是 ( )
3.下列平移作图错误的是 ( )
4.下列图形既是轴对称图形又是中心对称图形的是 ( )
5.如图,△ABC≌△BAD,若AB=6 cm,AC=3 cm,BC=5 cm,则AD的长为 ( )
A.3 cm
B.5 cm
C.6 cm
D.以上都不对
6.如图,这是台球桌面示意图,阴影部分表示四个入球孔,小明按图中所示方向击球(球可以多次反弹),则球最后落入的球袋是 ( )
A.1号袋
B.2号袋
C.3号袋
D.4号袋
7.把图中的五角星图案绕着它的中心点O进行旋转,若五角星旋转后与自身重合,则至少需旋转 ( )
A.36°
B.45°
C.72°
D.90°
8.如图,将△ABC沿着由点B到点C的方向平移得到△DEF,已知BC=12,EC=8,那么平移的距离为 ( )
A.20 B.12 C.8 D.4
9.在如图所示的4×4的正方形网格中,△PMN绕某一点旋转一定的角度,得到△P1M1N1,其旋转中心是 ( )
A.点A B.点B C.点C D.点D
10.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中与△ABC成轴对称的格点三角形最多能画出 ( )
A.6个 B.5个 C.4个 D.3个
二、填空题(每小题3分,共15分)
11.如图,AC=1,△DEC 与△ABC关于点C中心对称,则AD的长是 .
12.如图,四边形ABCD≌四边形A'B'C'D',则∠A的大小是 .
13.一个正n边形绕它的中心至少旋转18°才能与原来的图形完全重合,则n的值为 .
14.如图,两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起,固定三角形ABC不动,将三角形DEF向右平移,当点E和点C重合时,停止移动,设DE交AC于点G.则四边形ABEG的面积 四边形CGDF的面积.(填“大于”、“小于”或“等于”)
15.一副直角三角尺如图1所示摆放,现将含45°角的三角尺ADE固定不动,将含30°角的三角尺ABC绕顶点A顺时针转动(旋转角不超过180度),使两块三角尺有一组边互相平行.如图2,当∠BAD=15°时,BC∥DE.当90°<∠BAD<180°时,所有符合条件的∠BAD的度数为 .
三、解答题(本大题共8个小题,满分75分)
16.(1)(5分)如图1,网格中的△ABC与△DEF成轴对称,请用所学轴对称的知识在网格中作出△ABC与△DEF的对称轴l.
(2)(5分)如图2,请在网格中作出△ABC关于直线MN成轴对称的△A'B'C'.
17.(9分)在如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,点A平移到点D的位置,点B,C平移后的对应点分别是点E,F.
(1)画出平移后的△DEF.
(2)连接AD,CF,则这两条线段之间的关系是 .
(3)△DEF的面积为 .
18.(9分)画图:试画出下列正多边形的所有对称轴,并完成表格.
正多边形的边数 3 4 5 6 7 …
对称轴的条数 …
根据上表,猜想正n边形有 条对称轴.
19.(9分)如图,△ABC≌△DEF,∠A=80°,∠B=70°,AB=16,EH=6,求∠F的度数与DH的长.
20.(9分)如图,∠CAE=60°,∠C=70°,且AD⊥BC,如果△ABC经过旋转后与△ADE重合.
(1)旋转中心是哪个点
(2)旋转了多少度
(3)∠BAC的度数是多少
21.(9分)图1、图2、图3是3×3的正方形网格,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影(请在图1、图2、图3中依次作答,均只需要画出符合条件的一种情形):
(1)在图1中选取1个空白小正方形涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
(2)在图2中选取1个空白小正方形涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)在图3中选取2个空白小正方形涂上阴影,使5个阴影小正方形组成一个轴对称图形.
22.(10分)如图,在锐角△ABC中,AC=7 cm,S△ABC=14 cm2,AD平分∠BAC,M,N分别是边AD,AB上的动点.
(1)求△ABC 的边AC上高的长度.
(2)求BM+MN的最小值.
23.(10分)在学习了全等图形的知识后,同学们结合以前学习的三角形三边之间的关系展开了探究活动.
问题情境:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
探究展示:
飞天组的分析过程如下:将△ACD绕点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断出中线AD的取值范围.
小明代表飞天组上台讲解:如图1,将△ACD绕着点D逆时针旋转180°得到△EBD.
∵AD是BC边上的中线,
∴BD=CD,(依据①)
由旋转的性质得△BDE≌△CDA,
∴BE=AC=6,(依据②)
在△ABE中,由三角形的三边关系得AB-BE
(1)上述证明过程中的“依据①”和“依据②”分别是指:
依据①是 ;
依据②是 .
(2)对于这道题目,你还有不同的解法吗 若有,请写出来;若没有,请回答以下问题:解题时,条件中若出现“中点”“中线”字样时,应如何思考呢
(3)如图2,在 △ABC中,∠BAC=90°,AD是BC边上的中线,试作AC关于点D中心对称的BE;并求出∠ABE的度数.
参考答案
1.C 2.A 3.C 4.B 5.B 6.B 7.C 8.D 9.B 10.A
11.2 12.95° 13.20 14.等于
15.105°或135° 提示:如图,当AC∥DE时,∠BAD=∠DAE=45°;当BC∥AD时,∠DAB=∠B=60°;当BC∥AE时,∵∠EAB=∠B=60°,∴∠BAD=∠DAE+∠EAB=45°+60°=105°;当AB∥DE时,∵∠E=∠EAB=90°,∴∠BAD=∠DAE+∠EAB=45°+90°=135°.综上所述,当90°<∠BAD<180°时,∠BAD=105°或135°.
16.(1)解:如图1,直线l即为所作.
5分
(2)解:如图2,△A'B'C'即为所作.
5分
17.解:(1)如图,△DEF即为所求. 3分
(2)AD=CF,AD∥CF. 6分
(3)7. 9分
提示:S△DEF=×(2+4)×4-×2×3-×1×4=7.
18.解:作图如下,
3;4;5;6;7. 7分
n. 9分
19.解:∵∠A=80°,∠B=70°,
∴∠ACB=180°-∠A-∠B=30°. 2分
∵△ABC≌△DEF,AB=16,
∴∠F=∠ACB=30°,DE=AB=16. 6分
∵EH=6,
∴DH=16-6=10. 9分
20.解:(1)旋转中心是点A. 2分
(2)旋转的角度即为∠CAE=60°. 4分
(3)根据旋转的性质知,∠EAC=∠BAD=60°,∠C=∠E=70°. 5分
如图,设AD⊥BC于点F,
则∠AFB=90°,
∴在Rt△ABF中,∠B=90°-∠BAD=30°,
∴在△ABC中,∠BAC=180°-∠B-∠C=180°-30°-70°=80°. 9分
21.(1)如图1所示. 3分
(2)如图2所示.(答案不唯一) 6分
(3)如图3所示.(答案不唯一) 9分
22.解:(1)如图,作AC边上的高BE,垂足为E.
∵△ABC的面积是14 cm2,AC=7 cm,
∴×7×BE=14,
∴BE=4 cm. 4分
(2)如图,以AD为对称轴,作△ANM的对称图形,点N的对称点为点R.
∵AD平分∠CAB,△ABC为锐角三角形,
∴点R必在AC边上, 7分
∴MR=MN,
∴BM+MN=BM+MR,
∴BM+MN=BR≥BE,(垂线段最短)
∴BM+MN的最小值为4 cm. 10分
23.解:(1)依据①是中点的定义; 1分
依据②是全等三角形的对应边相等. 2分
(2)可以考虑构造以该中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中,从而解决问题. 5分
(3)如图,BE即为所求. 7分
易得△BDE≌△CDA,
∴∠E=∠CAD.
∵∠BAC=90°,
∴∠E+∠BAE=∠BAE+∠CAD=∠BAC=90°,
∴∠ABE=90°. 10分
2
