2023-2024学年初中数学沪科版七年级下册第10章 相交线、平行线与平移 单元练习(含答案)
文档属性
| 名称 | 2023-2024学年初中数学沪科版七年级下册第10章 相交线、平行线与平移 单元练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 253.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 06:59:28 | ||
图片预览



文档简介
第10章 相交线、平行线与平移
(时间:100分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A、B、C、D四个选项,其中只有一个是正确的,请把正确答案的代号填在下表中.
题号 1 2 3 4 5 6 7 8 9 10
答案
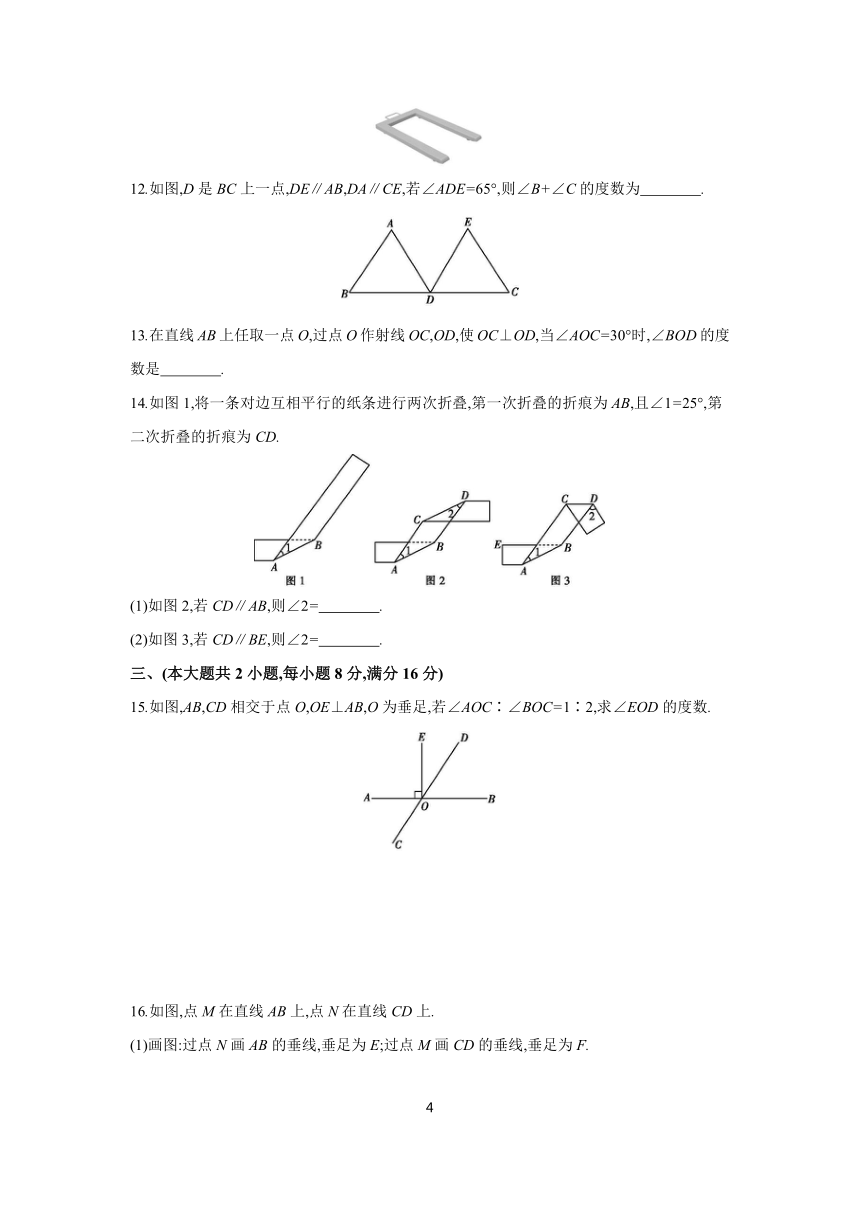
1.如图,∠1的同位角是( )
A.∠2
B.∠3
C.∠4
D.∠5
2.下列图形中,不能通过其中一个四边形平移得到的是( )
3.如图,小明同学的家在P处,他想尽快赶到附近公路边搭乘公交车,他选择P→C路线,用数学知识解释其道理正确的是( )
A.两点确定一条直线
B.两点之间线段最短
C.垂线段最短
D.三角形两边之和大于第三边
4.如果a∥b,b∥c,那么a∥c,这个推理的依据是
A.等量代换
B.平行线的定义
C.经过直线外一点,有且只有一条直线与已知直线平行
D.平行于同一直线的两直线平行
5.如图,直线a,b被直线c所截,则下列说法错误的是( )
A.∠1与∠2是邻补角
B.∠1与∠3是对顶角
C.∠2与∠4是同位角
D.∠3与∠4是内错角
6.如图,直线l1∥l2,点A,B在l2上,射线BD交l1于点D,BC平分∠ABD交l1于点C,若∠1=80°,则∠2的度数是( )
A.40°
B.50°
C.60°
D.80°
7.如图,点E在射线BC上,下列条件中能判断AD∥BC的是( )
A.∠1=∠2
B.∠1=∠3
C.∠2=∠4
D.∠3=∠4
8.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上平行行驶,那么两个拐弯的角度( )
A.先向左转130°,再向左转50°
B.先向左转50°,再向右转50°
C.先向左转50°,再向右转40°
D.先向左转50°,再向左转40°
9.如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的有( )
A.2个
B.3个
C.4个
D.5个
10.如图,已知△ABC的周长为20 cm,现将△ABC沿AB方向平移2 cm至△A'B'C'的位置,连接CC',则四边形AB'C'C的周长为( )
A.20 cm
B.22 cm
C.24 cm
D.26 cm
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,这是一个“U”型电子托盘秤,为了保证它的两边平行,把两个拐角处都设计成直角,这样设计的依据是 .
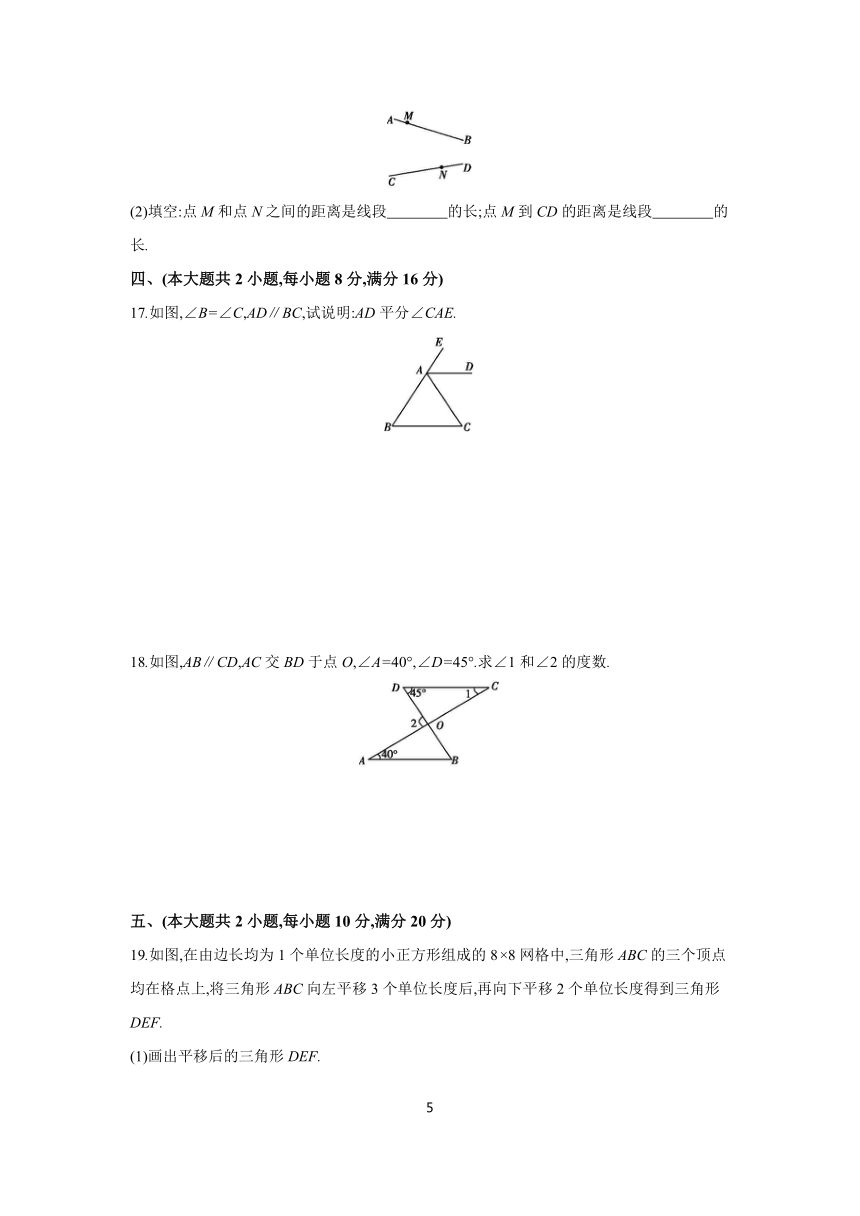
12.如图,D是BC上一点,DE∥AB,DA∥CE,若∠ADE=65°,则∠B+∠C的度数为 .
13.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是 .
14.如图1,将一条对边互相平行的纸条进行两次折叠,第一次折叠的折痕为AB,且∠1=25°,第二次折叠的折痕为CD.
(1)如图2,若CD∥AB,则∠2= .
(2)如图3,若CD∥BE,则∠2= .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,AB,CD相交于点O,OE⊥AB,O为垂足,若∠AOC∶∠BOC=1∶2,求∠EOD的度数.
16.如图,点M在直线AB上,点N在直线CD上.
(1)画图:过点N画AB的垂线,垂足为E;过点M画CD的垂线,垂足为F.
(2)填空:点M和点N之间的距离是线段 的长;点M到CD的距离是线段 的长.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,∠B=∠C,AD∥BC,试说明:AD平分∠CAE.
18.如图,AB∥CD,AC交BD于点O,∠A=40°,∠D=45°.求∠1和∠2的度数.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在由边长均为1个单位长度的小正方形组成的8×8网格中,三角形ABC的三个顶点均在格点上,将三角形ABC向左平移3个单位长度后,再向下平移2个单位长度得到三角形DEF.
(1)画出平移后的三角形DEF.
(2)若点A向左平移n个单位长度后落在三角形DEF的内部,请直接写出所有符合条件的整数n的值.
20.育才中学七年级(1)班开展社会实践活动,同学们到工厂去进行社会实践活动时,发现工人师傅生产了一种如图所示的零件,要求AB∥CD,∠BAE=32°,∠AED=78°.组员小林发现工人师傅量出∠BAE=32°,∠AED=78°后,又量出∠EDC=46°,请判断这个零件是否合格,并说明理由.
六、(本题满分12分)
21.如图,∠EDC=∠GFD,∠DEF+∠AGF=180°.
(1)判断AB与EF的位置关系,并说明理由.
(2)过点G作线段GH⊥EF,垂足为H,若∠DEF=30°,求∠FGH的度数.
七、(本题满分12分)
22.如图,∠B=∠DCG,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠AEB.
(1)若∠BAD=98°,求∠ADC的度数.
(2)AD与BC是什么位置关系 并说明理由.
(3)若∠DAB=α,∠G=β,直接写出当α,β满足什么数量关系时,AE∥DG.
八、(本题满分14分)
23.如图,AM∥BN,∠A=60°,P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数.
(2)当点P运动时,∠APB∶∠ADB的比值是否随之变化 若不变,请求出这个比值;若变化,请找出变化规律.
(3)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数.
参考答案
1.A 2.B 3.C 4.D 5.D 6.B 7.B 8.B 9.D
10.C 提示:根据题意,得A的对应点为A',B的对应点为B',C的对应点为C',所以BC=B'C',BB'=CC',则四边形AB'C'C的周长=CA+AB+BB'+B'C'+C'C=△ABC的周长+2BB'=20+4=24(cm).故选C.
11.同旁内角互补,两直线平行 12.115° 13.60°或120°
14.(1)25° (2)80° 提示:(1)因为CD∥AB,所以∠1+∠ACD=180°.因为∠1=25°,所以∠ACD=180°-25°=155°.因为AC∥BD,所以∠ACD+∠2=180°,所以∠2=180°-∠ACD=25°,故答案为25°.
(2)如图,
由折叠的性质,可得∠3=∠1=25°.因为EB∥AM,所以∠4=∠1+∠3=50°.因为AC∥BD,所以∠4+∠EBD=180°,所以∠EBD=180°-∠4=130°.又因为CD∥BE,所以∠EBD+∠BDC=180°,所以∠BDC=50°,由折叠的性质,可得2∠BDC+∠2=180°,所以∠2=180°-100°=80°,故答案为80°.
15.解:因为∠AOC∶∠BOC=1∶2,
所以∠BOC=2∠AOC. 2分
因为∠AOC+∠BOC=180°,
所以∠AOC=60°,
所以∠BOD=∠AOC=60°. 6分
因为OE⊥AB,
所以∠EOB=90°,
所以∠EOD=∠EOB-∠BOD=30°. 8分
16.解:(1)如图所示.
4分
(2)MN;MF. 8分
17.证明:因为AD∥BC(已知),
所以∠B=∠EAD(两直线平行,同位角相等), 2分
∠DAC=∠C(两直线平行,内错角相等). 4分
又因为∠B=∠C(已知),
所以∠EAD=∠DAC(等量代换),
所以AD平分∠CAE(角平分线的定义). 8分
18.解:因为AB∥CD,
所以∠1=∠A. 1分
因为∠A=40°,
所以∠1=40°. 3分
如图,过点O作OE∥AB,所以OE∥AB∥CD,
所以∠D=∠DOE,∠A=∠AOE,
所以∠2=∠A+∠D.
因为∠D=45°,所以∠2=85°. 6分
由上可得,∠1的度数是40°,∠2的度数是85°. 8分
19.解:(1)如图,三角形ABC即为所求.
6分
(2)由图可知,n=3或4. 10分
20.解:这个零件合格. 2分
理由:如图,在∠AED内部画∠AEF=∠BAE, 3分
所以EF∥AB. 4分
又因为∠BAE=32°,∠AED=78°,
所以∠DEF=46°. 6分
又因为∠EDC=46°,所以∠DEF=∠EDC,
所以EF∥CD, 8分
所以AB∥CD.故此零件合格. 10分
21.解:(1)AB∥EF. 2分
理由:因为∠EDC=∠GFD,
所以DE∥GF, 4分
所以∠DEF=∠GFE.
因为∠DEF+∠AGF=180°,
所以∠GFE+∠AGF=180°,
所以AB∥EF. 6分
(2)如图,因为GH⊥EF,
所以∠GHF=90°. 8分
因为GF∥DE,∠DEF=30°,
所以∠GFE=∠DEF=30°, 10分
所以∠FGH=180°-∠GHF-∠GFE=180°-90°-30°=60°. 12分
22.解:(1)因为∠B=∠DCG,
所以AB∥CD,
所以∠BAD+∠ADC=180°. 2分
又因为∠BAD=98°,
所以∠ADC=180°-∠BAD=82°. 4分
(2)AD∥BC. 5分
理由:因为AB∥CD,
所以∠BAF=∠CFE.
因为AE平分∠BAD,
所以∠BAF=∠FAD,
所以∠FAD=∠CFE. 7分
因为∠CFE=∠AEB,
所以∠FAD=∠AEB,
所以AD∥BC. 9分
(3)当β=α时,AE∥DG. 12分
提示:因为AD∥BC,
所以∠DAF=∠AEB.
因为AE平分∠BAD,
所以∠DAB=2∠DAF=2∠AEB.
因为∠DAB=α,
所以α=2∠DAF=2∠AEB,
所以∠AEB=α.
因为∠G=β,
所以当β=α时,AE∥DG.
23.解:(1)因为AM∥BN,
所以∠ABN=180°-∠A=120°.
又因为BC,BD分别平分∠ABP和∠PBN,
所以∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN)=∠ABN=60°. 3分
(2)不变. 4分
理由如下:因为AM∥BN,
所以∠APB=∠PBN,∠ADB=∠DBN. 6分
又因为BD平分∠PBN,
所以∠ADB=∠DBN=∠PBN=∠APB,即∠APB∶∠ADB=2∶1. 8分
(3)因为AM∥BN,
所以∠ACB=∠CBN. 10分
又因为∠ACB=∠ABD,
所以∠CBN=∠ABD,
所以∠ABC=∠ABD-∠CBD=∠CBN-∠CBD=∠DBN, 12分
所以∠ABC=∠CBP=∠DBP=∠DBN,
所以∠ABC=∠ABN=30°. 14分
2
(时间:100分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A、B、C、D四个选项,其中只有一个是正确的,请把正确答案的代号填在下表中.
题号 1 2 3 4 5 6 7 8 9 10
答案
1.如图,∠1的同位角是( )
A.∠2
B.∠3
C.∠4
D.∠5
2.下列图形中,不能通过其中一个四边形平移得到的是( )
3.如图,小明同学的家在P处,他想尽快赶到附近公路边搭乘公交车,他选择P→C路线,用数学知识解释其道理正确的是( )
A.两点确定一条直线
B.两点之间线段最短
C.垂线段最短
D.三角形两边之和大于第三边
4.如果a∥b,b∥c,那么a∥c,这个推理的依据是
A.等量代换
B.平行线的定义
C.经过直线外一点,有且只有一条直线与已知直线平行
D.平行于同一直线的两直线平行
5.如图,直线a,b被直线c所截,则下列说法错误的是( )
A.∠1与∠2是邻补角
B.∠1与∠3是对顶角
C.∠2与∠4是同位角
D.∠3与∠4是内错角
6.如图,直线l1∥l2,点A,B在l2上,射线BD交l1于点D,BC平分∠ABD交l1于点C,若∠1=80°,则∠2的度数是( )
A.40°
B.50°
C.60°
D.80°
7.如图,点E在射线BC上,下列条件中能判断AD∥BC的是( )
A.∠1=∠2
B.∠1=∠3
C.∠2=∠4
D.∠3=∠4
8.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上平行行驶,那么两个拐弯的角度( )
A.先向左转130°,再向左转50°
B.先向左转50°,再向右转50°
C.先向左转50°,再向右转40°
D.先向左转50°,再向左转40°
9.如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的有( )
A.2个
B.3个
C.4个
D.5个
10.如图,已知△ABC的周长为20 cm,现将△ABC沿AB方向平移2 cm至△A'B'C'的位置,连接CC',则四边形AB'C'C的周长为( )
A.20 cm
B.22 cm
C.24 cm
D.26 cm
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,这是一个“U”型电子托盘秤,为了保证它的两边平行,把两个拐角处都设计成直角,这样设计的依据是 .
12.如图,D是BC上一点,DE∥AB,DA∥CE,若∠ADE=65°,则∠B+∠C的度数为 .
13.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是 .
14.如图1,将一条对边互相平行的纸条进行两次折叠,第一次折叠的折痕为AB,且∠1=25°,第二次折叠的折痕为CD.
(1)如图2,若CD∥AB,则∠2= .
(2)如图3,若CD∥BE,则∠2= .
三、(本大题共2小题,每小题8分,满分16分)
15.如图,AB,CD相交于点O,OE⊥AB,O为垂足,若∠AOC∶∠BOC=1∶2,求∠EOD的度数.
16.如图,点M在直线AB上,点N在直线CD上.
(1)画图:过点N画AB的垂线,垂足为E;过点M画CD的垂线,垂足为F.
(2)填空:点M和点N之间的距离是线段 的长;点M到CD的距离是线段 的长.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,∠B=∠C,AD∥BC,试说明:AD平分∠CAE.
18.如图,AB∥CD,AC交BD于点O,∠A=40°,∠D=45°.求∠1和∠2的度数.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在由边长均为1个单位长度的小正方形组成的8×8网格中,三角形ABC的三个顶点均在格点上,将三角形ABC向左平移3个单位长度后,再向下平移2个单位长度得到三角形DEF.
(1)画出平移后的三角形DEF.
(2)若点A向左平移n个单位长度后落在三角形DEF的内部,请直接写出所有符合条件的整数n的值.
20.育才中学七年级(1)班开展社会实践活动,同学们到工厂去进行社会实践活动时,发现工人师傅生产了一种如图所示的零件,要求AB∥CD,∠BAE=32°,∠AED=78°.组员小林发现工人师傅量出∠BAE=32°,∠AED=78°后,又量出∠EDC=46°,请判断这个零件是否合格,并说明理由.
六、(本题满分12分)
21.如图,∠EDC=∠GFD,∠DEF+∠AGF=180°.
(1)判断AB与EF的位置关系,并说明理由.
(2)过点G作线段GH⊥EF,垂足为H,若∠DEF=30°,求∠FGH的度数.
七、(本题满分12分)
22.如图,∠B=∠DCG,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠AEB.
(1)若∠BAD=98°,求∠ADC的度数.
(2)AD与BC是什么位置关系 并说明理由.
(3)若∠DAB=α,∠G=β,直接写出当α,β满足什么数量关系时,AE∥DG.
八、(本题满分14分)
23.如图,AM∥BN,∠A=60°,P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数.
(2)当点P运动时,∠APB∶∠ADB的比值是否随之变化 若不变,请求出这个比值;若变化,请找出变化规律.
(3)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数.
参考答案
1.A 2.B 3.C 4.D 5.D 6.B 7.B 8.B 9.D
10.C 提示:根据题意,得A的对应点为A',B的对应点为B',C的对应点为C',所以BC=B'C',BB'=CC',则四边形AB'C'C的周长=CA+AB+BB'+B'C'+C'C=△ABC的周长+2BB'=20+4=24(cm).故选C.
11.同旁内角互补,两直线平行 12.115° 13.60°或120°
14.(1)25° (2)80° 提示:(1)因为CD∥AB,所以∠1+∠ACD=180°.因为∠1=25°,所以∠ACD=180°-25°=155°.因为AC∥BD,所以∠ACD+∠2=180°,所以∠2=180°-∠ACD=25°,故答案为25°.
(2)如图,
由折叠的性质,可得∠3=∠1=25°.因为EB∥AM,所以∠4=∠1+∠3=50°.因为AC∥BD,所以∠4+∠EBD=180°,所以∠EBD=180°-∠4=130°.又因为CD∥BE,所以∠EBD+∠BDC=180°,所以∠BDC=50°,由折叠的性质,可得2∠BDC+∠2=180°,所以∠2=180°-100°=80°,故答案为80°.
15.解:因为∠AOC∶∠BOC=1∶2,
所以∠BOC=2∠AOC. 2分
因为∠AOC+∠BOC=180°,
所以∠AOC=60°,
所以∠BOD=∠AOC=60°. 6分
因为OE⊥AB,
所以∠EOB=90°,
所以∠EOD=∠EOB-∠BOD=30°. 8分
16.解:(1)如图所示.
4分
(2)MN;MF. 8分
17.证明:因为AD∥BC(已知),
所以∠B=∠EAD(两直线平行,同位角相等), 2分
∠DAC=∠C(两直线平行,内错角相等). 4分
又因为∠B=∠C(已知),
所以∠EAD=∠DAC(等量代换),
所以AD平分∠CAE(角平分线的定义). 8分
18.解:因为AB∥CD,
所以∠1=∠A. 1分
因为∠A=40°,
所以∠1=40°. 3分
如图,过点O作OE∥AB,所以OE∥AB∥CD,
所以∠D=∠DOE,∠A=∠AOE,
所以∠2=∠A+∠D.
因为∠D=45°,所以∠2=85°. 6分
由上可得,∠1的度数是40°,∠2的度数是85°. 8分
19.解:(1)如图,三角形ABC即为所求.
6分
(2)由图可知,n=3或4. 10分
20.解:这个零件合格. 2分
理由:如图,在∠AED内部画∠AEF=∠BAE, 3分
所以EF∥AB. 4分
又因为∠BAE=32°,∠AED=78°,
所以∠DEF=46°. 6分
又因为∠EDC=46°,所以∠DEF=∠EDC,
所以EF∥CD, 8分
所以AB∥CD.故此零件合格. 10分
21.解:(1)AB∥EF. 2分
理由:因为∠EDC=∠GFD,
所以DE∥GF, 4分
所以∠DEF=∠GFE.
因为∠DEF+∠AGF=180°,
所以∠GFE+∠AGF=180°,
所以AB∥EF. 6分
(2)如图,因为GH⊥EF,
所以∠GHF=90°. 8分
因为GF∥DE,∠DEF=30°,
所以∠GFE=∠DEF=30°, 10分
所以∠FGH=180°-∠GHF-∠GFE=180°-90°-30°=60°. 12分
22.解:(1)因为∠B=∠DCG,
所以AB∥CD,
所以∠BAD+∠ADC=180°. 2分
又因为∠BAD=98°,
所以∠ADC=180°-∠BAD=82°. 4分
(2)AD∥BC. 5分
理由:因为AB∥CD,
所以∠BAF=∠CFE.
因为AE平分∠BAD,
所以∠BAF=∠FAD,
所以∠FAD=∠CFE. 7分
因为∠CFE=∠AEB,
所以∠FAD=∠AEB,
所以AD∥BC. 9分
(3)当β=α时,AE∥DG. 12分
提示:因为AD∥BC,
所以∠DAF=∠AEB.
因为AE平分∠BAD,
所以∠DAB=2∠DAF=2∠AEB.
因为∠DAB=α,
所以α=2∠DAF=2∠AEB,
所以∠AEB=α.
因为∠G=β,
所以当β=α时,AE∥DG.
23.解:(1)因为AM∥BN,
所以∠ABN=180°-∠A=120°.
又因为BC,BD分别平分∠ABP和∠PBN,
所以∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN)=∠ABN=60°. 3分
(2)不变. 4分
理由如下:因为AM∥BN,
所以∠APB=∠PBN,∠ADB=∠DBN. 6分
又因为BD平分∠PBN,
所以∠ADB=∠DBN=∠PBN=∠APB,即∠APB∶∠ADB=2∶1. 8分
(3)因为AM∥BN,
所以∠ACB=∠CBN. 10分
又因为∠ACB=∠ABD,
所以∠CBN=∠ABD,
所以∠ABC=∠ABD-∠CBD=∠CBN-∠CBD=∠DBN, 12分
所以∠ABC=∠CBP=∠DBP=∠DBN,
所以∠ABC=∠ABN=30°. 14分
2
