第20章 数据的初步分析单元练习(含答案) 2023-2024学年初中数学沪科版八年级下册
文档属性
| 名称 | 第20章 数据的初步分析单元练习(含答案) 2023-2024学年初中数学沪科版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 226.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 00:00:00 | ||
图片预览




文档简介
第20章 数据的初步分析
(时间:120分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A、B、C、D四个选项,其中只有一个是正确的,请把正确答案的代号填在下表中.
题号 1 2 3 4 5 6 7 8 9 10
答案
1.在数据1,3,5,7,9中再添加一个数据,使得该组数据的平均数不变,则添加的数据为( )
A.25 B.3 C.4.5 D.5
2.已知样本数据个数为30,且被分成4组,各组数据个数之比为2∶3∶4∶1,则第二小组频数和第三小组的频率分别为( )
A.0.4和0.3 B.0.4和9
C.9和0.4 D.12和9
3.一个容量为80的数字样本,其最大值是133,最小值是51.若确定组距为10,则可以分成( )
A.10组 B.9组 C.8组 D.7组
4.“积极行动起来,共建节约型社会!”我市某小区200户居民参加了节水行动,现统计了10户家庭一个月的节水情况,将有关数据整理如下:( )
节水量(单位:吨) 0.5 1 1.5 2
家庭数(单位:户) 2 3 4 1
请你估计该小区200户居民一个月节约用水的总量是( )
A.180吨 B.200吨 C.240吨 D.360吨
5.下表是某校女子羽毛球队12名队员的年龄分布:
年龄/岁 13 14 15 16
人数 1 5 4 2
则关于这12名队员的年龄的说法正确的是( )
A.平均数是14 B.中位数是15
C.众数是14 D.众数是5
6.某校举办了以“红心颂党恩,喜迎二十大”为主题的演讲比赛.已知某位选手在演讲内容、演讲结构、演讲表达三项的得分分别为94分,80分,90分,若依次按照50%,30%,20%的百分比确定成绩,则该选手的成绩是( )
A.85分 B.88分 C.89分 D.90分
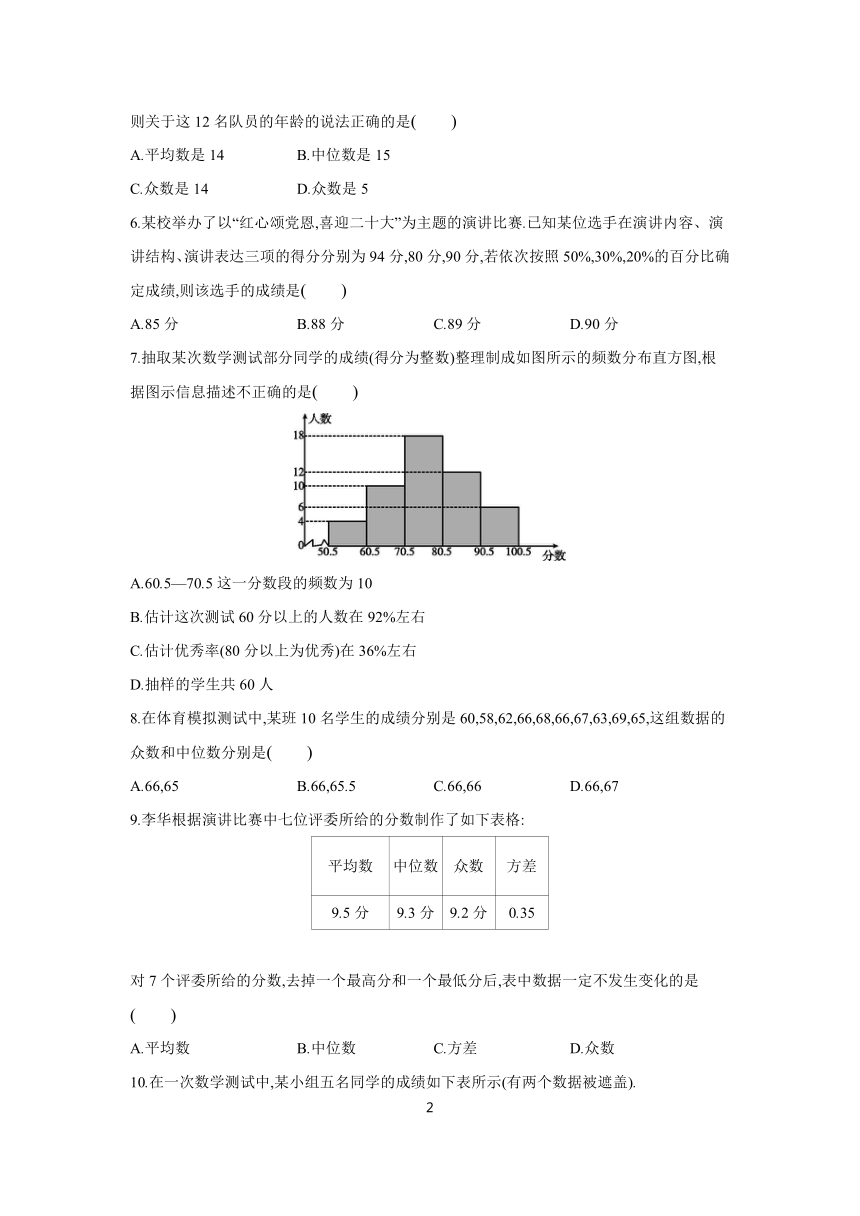
7.抽取某次数学测试部分同学的成绩(得分为整数)整理制成如图所示的频数分布直方图,根据图示信息描述不正确的是( )
A.60.5—70.5这一分数段的频数为10
B.估计这次测试60分以上的人数在92%左右
C.估计优秀率(80分以上为优秀)在36%左右
D.抽样的学生共60人
8.在体育模拟测试中,某班10名学生的成绩分别是60,58,62,66,68,66,67,63,69,65,这组数据的众数和中位数分别是( )
A.66,65 B.66,65.5 C.66,66 D.66,67
9.李华根据演讲比赛中七位评委所给的分数制作了如下表格:
平均数 中位数 众数 方差
9.5分 9.3分 9.2分 0.35
对7个评委所给的分数,去掉一个最高分和一个最低分后,表中数据一定不发生变化的是( )
A.平均数 B.中位数 C.方差 D.众数
10.在一次数学测试中,某小组五名同学的成绩如下表所示(有两个数据被遮盖).
组员 甲 乙 丙 丁 戊 方差 平均成绩
得分 81 79 ■ 80 82 ■ 80
那么被遮盖的两个数据依次是( )
A.78,3 B.78,2 C.80, D.80,2
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,这是九(1)班45名同学每周课外阅读时间的频数分布直方图(每组含前一个边界值,不含后一个边界值).其中每周课外阅读时间在6小时及以上的人有 名.
12.两组数据3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为 .
13.中药是以我国传统医药理论为指导,经过采集、炮制、制剂而得到的药物.在一个时间段,某中药房的黄芪、焦山楂、当归三种中药的销售单价和销售额情况如表:
中药 黄芪 焦山楂 当归
销售单价(单位:元/千克) 80 60 90
销售额(单位:元) 120 120 360
则在这个时间段,该中药房的这三种中药的平均销售量为 千克.
14.某校在“爱护地球,绿化祖国”的创建活动中,组织学生开展植树造林活动.为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表所示.
植树数量(单位:棵) 4 5 6 8 10
人数 28 20 25 16 11
(1)这100名同学平均每人植树 棵.
(2)若该校共有1000名学生,请根据以上调查结果估计该校学生的植树总棵数是 .
三、(本大题共2小题,每小题8分,满分16分)
15.小花最近买了三本课外书,分别是A.《汉语字典》,B.《流行杂志》和C.《故事大王》.班里的同学都很喜欢借阅,在五天内小花做了借书记录如下表:
书名代号 星期一 星期二 星期三 星期四 星期五 借阅频数
A 3 2 2 3 4
B 4 3 3 2 3
C 1 2 3 2 3
(1)在表中填写五天内每本书的借阅频数.
(2)计算五天内《汉语字典》的借阅频率.
16.某公司欲招聘一名工作人员,对甲、乙两位应聘者进行了听、说、读、写的测试,他们的成绩(单位:分)如下表所示.
候选人 听 说 读 写
甲 8 9 8 7
乙 9 8 6 8
(1)如果听、说、读、写同样重要,应录取谁
(2)如果听、说、读、写按4∶2∶1∶3来计算,应录取谁
四、(本大题共2小题,每小题8分,满分16分)
17.随着智能手机的普及,抢微信红包成为了春节期间人们最喜欢的活动之一.某中学八(5)班50名学生在春节期间所抢的红包金额统计图如下.根据图中提供的信息,分别求出红包金额的众数和中位数.
18.一组数据3,4,6,8,x的中位数是x,且x是满足不等式组的整数,求这组数据的平均数.
五、(本大题共2小题,每小题10分,满分20分)
19.某市一家园林公司培育出新品种树苗,为考察这种树苗的移植成活率,公司进行了统计,结果如下表所示.
累积移植总数/棵 100 500 1000 2000 5000 10000
成活率 0.910 0.968 0.942 0.956 0.947 0.950
现该市实施绿化工程,需移植一批这种树苗,若这批树苗移植后要有28.5万棵成活,则需要一次性移植多少棵树苗较为合适 请说明理由.
20.为响应“全民阅读”号召,某校在七年级800名学生中随机抽取100名学生,对该部分学生在一年时间内阅读中外名著的情况进行调查,整理调查结果发现,学生阅读中外名著的本数最少的有5本,最多的有8本,并根据调查结果绘制了如图所示的不完整的条形统计图,其中阅读了6本的人数占被调查人数的30%.根据图中提供的信息,补全条形统计图并估计该校七年级全体学生在该年阅读中外名著的总本数.
七年级部分学生阅读中外名著本数条形统计图
六、(本题满分12分)
21.某校从八年级(1)班和(2)班中各选取10名女同学,量得她们的身高(单位:厘米)如下:
(1)班:168 167 170 165 168 166 171 168 167 170
(2)班:165 167 169 170 165 168 170 171 168 167
(1)补充完成下面的统计分析表.
班级 平均数 方差 中位数
1班 168 168
2班 3.8
(2)若该校要从这两个班中选取一个班的10名女同学组成礼仪队,请你选一个合适的统计量作为选择标准,说明哪一个班能被选取.
七、(本题满分12分)
22.某学校在暑假期间开展“心怀感恩,孝敬父母”的实践活动,倡导学生在假期中帮助父母干家务.开学以后,校学生会随机抽取了部分学生,就暑假“平均每天帮助父母干家务所用时长”进行了调査,以下是根据相关数据绘制的统计图的一部分:
(注:每组数据包含左端值,不包含右端值)
根据上述信息,回答下列问题:
(1)在本次随机抽取的样本中,调查的学生人数是 .
(2)m= ,n= .
(3)补全频数分布直方图.
(4)如果该校共有学生1000人,请你估计“平均每天帮助父母干家务的时长不少于30分钟”的学生人数.
八、(本题满分14分)
23.某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,乙的5次射击得分分别为7环,5环,7环,a环,7环,小宇根据他们的成绩绘制了如下尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
(1)a= ,= .
(2)请完成折线图中表示乙成绩变化情况的折线.
(3)①观察折线图,可看出 的成绩比较稳定(填“甲”或“乙”).参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.
②请你从平均数和方差的角度分析,谁将被选中.
参考答案
1.D 2.C 3.B 4.C 5.C 6.C 7.D 8.B 9.B 10.B
11.14 12.6 13.2.5 14.(1)6 (2)6000
15.解:(1)填表如下:
书名代号 星期一 星期二 星期三 星期四 星期五 借阅频数
A 3 2 2 3 4 14
B 4 3 3 2 3 15
C 1 2 3 2 3 11
3分
(2)总数是14+15+11=40, 5分
则五天内《汉语字典》的借阅频率是==0.35. 8分
16.解:(1)甲的平均成绩是=8(分),
乙的平均成绩是=7.75(分),
因为甲的平均成绩大于乙的平均成绩,
所以如果听、说、读、写同样重要,甲将被录取. 4分
(2)甲的平均成绩为(8×4+9×2+8×1+7×3)÷10=7.9(分),
乙的平均成绩为(9×4+8×2+6×1+8×3)÷10=8.2(分),
因为乙的平均分数较高,所以乙将被录取. 8分
17.解:红包金额为30元的人数有20人,最多,则众数为30. 4分
中间两个数分别为30和30,则中位数是30. 8分
18.解:解不等式组得3≤x<5. 2分
∵x是整数,∴x=3或4. 4分
当x=3时,3,4,6,8,x的中位数是4(不合题意,舍去). 5分
当x=4时,3,4,6,8,x的中位数是4,符合题意. 6分
则这组数据的平均数是(3+4+6+8+4)÷5=5. 8分
19.解:由表格可知,随着树苗移植数量的增加,树苗移植成活率越来越稳定.
当移植总数为10000时,成活率为0.950,于是可以估计树苗移植成活率为0.950, 5分
则该市需要一次性移植的树苗数量约为28.5÷0.950=30万棵. 10分
20.解:根据题意可知,阅读了6本的人数为100×30%=30人,
阅读了7本的人数为100-20-30-15=35人.
补全条形图如下:
七年级部分学生阅读中外名著本数条形统计图
4分
∵平均每位学生的阅读数量为=6.45(本), 7分
∴估计该校七年级全体学生在该年阅读中外名著的总本数为800×6.45=5160本.
答:估计该校七年级全体学生在该年阅读中外名著的总本数约为5160本. 10分
21.解:(1)补全表格如下:
班级 平均数 方差 中位数
(1)班 168 3.2 168
(2)班 168 3.8 168
6分
(2)选择方差作为标准, 8分
∵(1)班的方差<(2)班的方差,∴(1)班可能被选取. 12分
22.解:(1)200. 2分
(2)20;25. 6分
(3)补全的频数分布直方图如图所示. 9分
(4)1000×=300(人),
即“平均每天帮助父母干家务的时长不少于30分钟”的学生大约有300人. 12分
23.解:(1)4,6. 4分
(2)如图.
7分
(3)①乙, 9分
=[(7-6)2+(5-6)2+(7-6)2+(4-6)2+(7-6)2]=1.6.
由于<,所以上述判断正确. 12分
②因为两人成绩的平均水平(平均数)相同,乙的成绩比甲稳定,所以乙将被选中. 14分
2
(时间:120分钟 分值:150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A、B、C、D四个选项,其中只有一个是正确的,请把正确答案的代号填在下表中.
题号 1 2 3 4 5 6 7 8 9 10
答案
1.在数据1,3,5,7,9中再添加一个数据,使得该组数据的平均数不变,则添加的数据为( )
A.25 B.3 C.4.5 D.5
2.已知样本数据个数为30,且被分成4组,各组数据个数之比为2∶3∶4∶1,则第二小组频数和第三小组的频率分别为( )
A.0.4和0.3 B.0.4和9
C.9和0.4 D.12和9
3.一个容量为80的数字样本,其最大值是133,最小值是51.若确定组距为10,则可以分成( )
A.10组 B.9组 C.8组 D.7组
4.“积极行动起来,共建节约型社会!”我市某小区200户居民参加了节水行动,现统计了10户家庭一个月的节水情况,将有关数据整理如下:( )
节水量(单位:吨) 0.5 1 1.5 2
家庭数(单位:户) 2 3 4 1
请你估计该小区200户居民一个月节约用水的总量是( )
A.180吨 B.200吨 C.240吨 D.360吨
5.下表是某校女子羽毛球队12名队员的年龄分布:
年龄/岁 13 14 15 16
人数 1 5 4 2
则关于这12名队员的年龄的说法正确的是( )
A.平均数是14 B.中位数是15
C.众数是14 D.众数是5
6.某校举办了以“红心颂党恩,喜迎二十大”为主题的演讲比赛.已知某位选手在演讲内容、演讲结构、演讲表达三项的得分分别为94分,80分,90分,若依次按照50%,30%,20%的百分比确定成绩,则该选手的成绩是( )
A.85分 B.88分 C.89分 D.90分
7.抽取某次数学测试部分同学的成绩(得分为整数)整理制成如图所示的频数分布直方图,根据图示信息描述不正确的是( )
A.60.5—70.5这一分数段的频数为10
B.估计这次测试60分以上的人数在92%左右
C.估计优秀率(80分以上为优秀)在36%左右
D.抽样的学生共60人
8.在体育模拟测试中,某班10名学生的成绩分别是60,58,62,66,68,66,67,63,69,65,这组数据的众数和中位数分别是( )
A.66,65 B.66,65.5 C.66,66 D.66,67
9.李华根据演讲比赛中七位评委所给的分数制作了如下表格:
平均数 中位数 众数 方差
9.5分 9.3分 9.2分 0.35
对7个评委所给的分数,去掉一个最高分和一个最低分后,表中数据一定不发生变化的是( )
A.平均数 B.中位数 C.方差 D.众数
10.在一次数学测试中,某小组五名同学的成绩如下表所示(有两个数据被遮盖).
组员 甲 乙 丙 丁 戊 方差 平均成绩
得分 81 79 ■ 80 82 ■ 80
那么被遮盖的两个数据依次是( )
A.78,3 B.78,2 C.80, D.80,2
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,这是九(1)班45名同学每周课外阅读时间的频数分布直方图(每组含前一个边界值,不含后一个边界值).其中每周课外阅读时间在6小时及以上的人有 名.
12.两组数据3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为 .
13.中药是以我国传统医药理论为指导,经过采集、炮制、制剂而得到的药物.在一个时间段,某中药房的黄芪、焦山楂、当归三种中药的销售单价和销售额情况如表:
中药 黄芪 焦山楂 当归
销售单价(单位:元/千克) 80 60 90
销售额(单位:元) 120 120 360
则在这个时间段,该中药房的这三种中药的平均销售量为 千克.
14.某校在“爱护地球,绿化祖国”的创建活动中,组织学生开展植树造林活动.为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表所示.
植树数量(单位:棵) 4 5 6 8 10
人数 28 20 25 16 11
(1)这100名同学平均每人植树 棵.
(2)若该校共有1000名学生,请根据以上调查结果估计该校学生的植树总棵数是 .
三、(本大题共2小题,每小题8分,满分16分)
15.小花最近买了三本课外书,分别是A.《汉语字典》,B.《流行杂志》和C.《故事大王》.班里的同学都很喜欢借阅,在五天内小花做了借书记录如下表:
书名代号 星期一 星期二 星期三 星期四 星期五 借阅频数
A 3 2 2 3 4
B 4 3 3 2 3
C 1 2 3 2 3
(1)在表中填写五天内每本书的借阅频数.
(2)计算五天内《汉语字典》的借阅频率.
16.某公司欲招聘一名工作人员,对甲、乙两位应聘者进行了听、说、读、写的测试,他们的成绩(单位:分)如下表所示.
候选人 听 说 读 写
甲 8 9 8 7
乙 9 8 6 8
(1)如果听、说、读、写同样重要,应录取谁
(2)如果听、说、读、写按4∶2∶1∶3来计算,应录取谁
四、(本大题共2小题,每小题8分,满分16分)
17.随着智能手机的普及,抢微信红包成为了春节期间人们最喜欢的活动之一.某中学八(5)班50名学生在春节期间所抢的红包金额统计图如下.根据图中提供的信息,分别求出红包金额的众数和中位数.
18.一组数据3,4,6,8,x的中位数是x,且x是满足不等式组的整数,求这组数据的平均数.
五、(本大题共2小题,每小题10分,满分20分)
19.某市一家园林公司培育出新品种树苗,为考察这种树苗的移植成活率,公司进行了统计,结果如下表所示.
累积移植总数/棵 100 500 1000 2000 5000 10000
成活率 0.910 0.968 0.942 0.956 0.947 0.950
现该市实施绿化工程,需移植一批这种树苗,若这批树苗移植后要有28.5万棵成活,则需要一次性移植多少棵树苗较为合适 请说明理由.
20.为响应“全民阅读”号召,某校在七年级800名学生中随机抽取100名学生,对该部分学生在一年时间内阅读中外名著的情况进行调查,整理调查结果发现,学生阅读中外名著的本数最少的有5本,最多的有8本,并根据调查结果绘制了如图所示的不完整的条形统计图,其中阅读了6本的人数占被调查人数的30%.根据图中提供的信息,补全条形统计图并估计该校七年级全体学生在该年阅读中外名著的总本数.
七年级部分学生阅读中外名著本数条形统计图
六、(本题满分12分)
21.某校从八年级(1)班和(2)班中各选取10名女同学,量得她们的身高(单位:厘米)如下:
(1)班:168 167 170 165 168 166 171 168 167 170
(2)班:165 167 169 170 165 168 170 171 168 167
(1)补充完成下面的统计分析表.
班级 平均数 方差 中位数
1班 168 168
2班 3.8
(2)若该校要从这两个班中选取一个班的10名女同学组成礼仪队,请你选一个合适的统计量作为选择标准,说明哪一个班能被选取.
七、(本题满分12分)
22.某学校在暑假期间开展“心怀感恩,孝敬父母”的实践活动,倡导学生在假期中帮助父母干家务.开学以后,校学生会随机抽取了部分学生,就暑假“平均每天帮助父母干家务所用时长”进行了调査,以下是根据相关数据绘制的统计图的一部分:
(注:每组数据包含左端值,不包含右端值)
根据上述信息,回答下列问题:
(1)在本次随机抽取的样本中,调查的学生人数是 .
(2)m= ,n= .
(3)补全频数分布直方图.
(4)如果该校共有学生1000人,请你估计“平均每天帮助父母干家务的时长不少于30分钟”的学生人数.
八、(本题满分14分)
23.某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,乙的5次射击得分分别为7环,5环,7环,a环,7环,小宇根据他们的成绩绘制了如下尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
(1)a= ,= .
(2)请完成折线图中表示乙成绩变化情况的折线.
(3)①观察折线图,可看出 的成绩比较稳定(填“甲”或“乙”).参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.
②请你从平均数和方差的角度分析,谁将被选中.
参考答案
1.D 2.C 3.B 4.C 5.C 6.C 7.D 8.B 9.B 10.B
11.14 12.6 13.2.5 14.(1)6 (2)6000
15.解:(1)填表如下:
书名代号 星期一 星期二 星期三 星期四 星期五 借阅频数
A 3 2 2 3 4 14
B 4 3 3 2 3 15
C 1 2 3 2 3 11
3分
(2)总数是14+15+11=40, 5分
则五天内《汉语字典》的借阅频率是==0.35. 8分
16.解:(1)甲的平均成绩是=8(分),
乙的平均成绩是=7.75(分),
因为甲的平均成绩大于乙的平均成绩,
所以如果听、说、读、写同样重要,甲将被录取. 4分
(2)甲的平均成绩为(8×4+9×2+8×1+7×3)÷10=7.9(分),
乙的平均成绩为(9×4+8×2+6×1+8×3)÷10=8.2(分),
因为乙的平均分数较高,所以乙将被录取. 8分
17.解:红包金额为30元的人数有20人,最多,则众数为30. 4分
中间两个数分别为30和30,则中位数是30. 8分
18.解:解不等式组得3≤x<5. 2分
∵x是整数,∴x=3或4. 4分
当x=3时,3,4,6,8,x的中位数是4(不合题意,舍去). 5分
当x=4时,3,4,6,8,x的中位数是4,符合题意. 6分
则这组数据的平均数是(3+4+6+8+4)÷5=5. 8分
19.解:由表格可知,随着树苗移植数量的增加,树苗移植成活率越来越稳定.
当移植总数为10000时,成活率为0.950,于是可以估计树苗移植成活率为0.950, 5分
则该市需要一次性移植的树苗数量约为28.5÷0.950=30万棵. 10分
20.解:根据题意可知,阅读了6本的人数为100×30%=30人,
阅读了7本的人数为100-20-30-15=35人.
补全条形图如下:
七年级部分学生阅读中外名著本数条形统计图
4分
∵平均每位学生的阅读数量为=6.45(本), 7分
∴估计该校七年级全体学生在该年阅读中外名著的总本数为800×6.45=5160本.
答:估计该校七年级全体学生在该年阅读中外名著的总本数约为5160本. 10分
21.解:(1)补全表格如下:
班级 平均数 方差 中位数
(1)班 168 3.2 168
(2)班 168 3.8 168
6分
(2)选择方差作为标准, 8分
∵(1)班的方差<(2)班的方差,∴(1)班可能被选取. 12分
22.解:(1)200. 2分
(2)20;25. 6分
(3)补全的频数分布直方图如图所示. 9分
(4)1000×=300(人),
即“平均每天帮助父母干家务的时长不少于30分钟”的学生大约有300人. 12分
23.解:(1)4,6. 4分
(2)如图.
7分
(3)①乙, 9分
=[(7-6)2+(5-6)2+(7-6)2+(4-6)2+(7-6)2]=1.6.
由于<,所以上述判断正确. 12分
②因为两人成绩的平均水平(平均数)相同,乙的成绩比甲稳定,所以乙将被选中. 14分
2
