高二数学抛物线课件
图片预览



文档简介
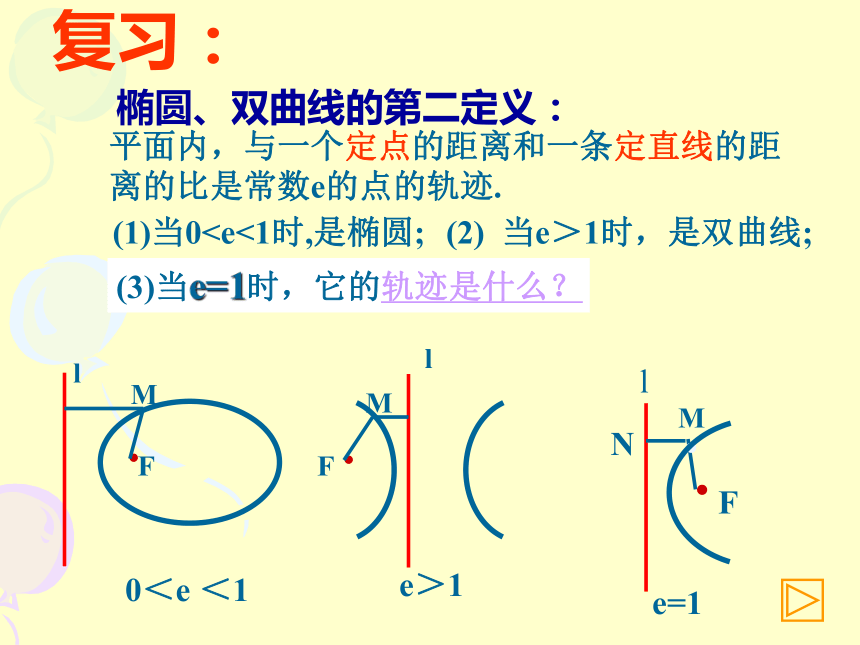
课件11张PPT。复习:椭圆、双曲线的第二定义:平面内,与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹.(2) 当e>1时,是双曲线;(3)当e=1时,它的轨迹是什么?(1)当0(1)焦点是(3,0);
(2)准线方程是x= - ;
(3)焦点到准线的距离是2;
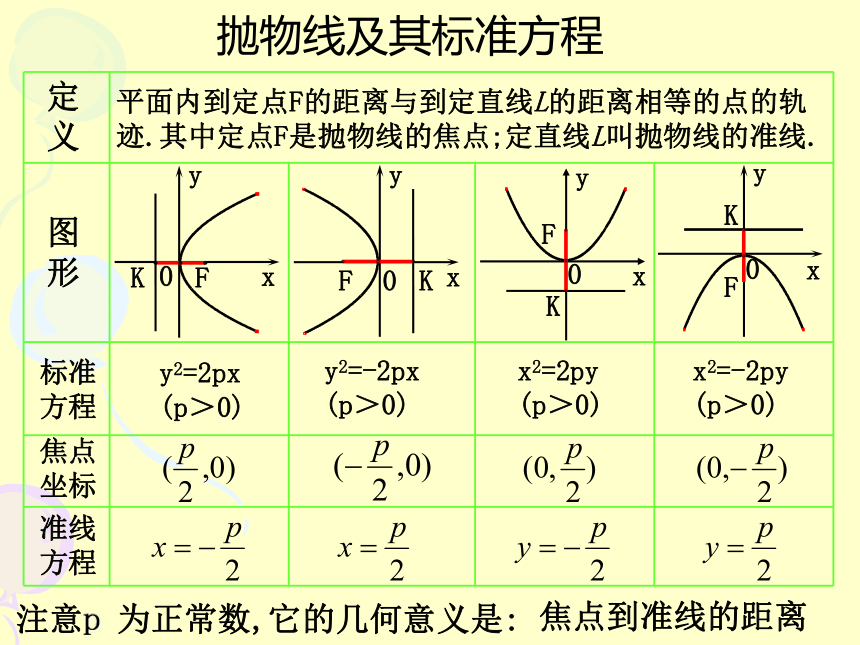
y2=12xy2=xy2=4xy2=-4xx2=4yx2=-4y例2、已知抛物线的焦点坐标是(0,-2),
求它的标准方程解:所以抛物线的标准方程是:F(5,0)F(0,-2)x=-5y=22、求下列抛物线的焦点坐标和准线 方程:
(1)y2=20x
(2)x2=(1/2)y
(3)2y2+5x=0
(4)x2+8y=03(1)抛物线y2=12x上与焦点的距离等于9的点坐标是__________.
(2)抛物线y2=2px(p>0)上一点M到焦点的距离是a(a>p/2),则点M到准线的距离是__________,点M的横坐标是________.
例3:斜率为1的直线经过y2=4x的焦点,与抛物线相交于两点A、B,求线段AB的长.例4:在抛物线y2=2x上求一点P,使得P到焦点F与到
点A(3,2)的距离之和最小,并求出最小值.Q解: 如图,设|PQ|为P到准线的距离则|PF|=|PQ|∴|AP|+|PF|=|AP|+|PQ|∴当A,P,Q共线时, |AP|+|PF|最小PQ思考:抛物线y2=2px(p>0)的点M到定点A(3,2)和焦点F的距离之和的最小值为5,求抛物线方程小结[1]抛物线的定义(可将两点距离与点线距离的相互转化) [2]标准方程有4种形式,要注意p的几何意义 [3]已知标准方程求焦点坐标或准线方程应先判断后求解 [4]已知焦点坐标或准线方程求抛物线的标准方程也是先判断后求解
(2)准线方程是x= - ;
(3)焦点到准线的距离是2;
y2=12xy2=xy2=4xy2=-4xx2=4yx2=-4y例2、已知抛物线的焦点坐标是(0,-2),
求它的标准方程解:所以抛物线的标准方程是:F(5,0)F(0,-2)x=-5y=22、求下列抛物线的焦点坐标和准线 方程:
(1)y2=20x
(2)x2=(1/2)y
(3)2y2+5x=0
(4)x2+8y=03(1)抛物线y2=12x上与焦点的距离等于9的点坐标是__________.
(2)抛物线y2=2px(p>0)上一点M到焦点的距离是a(a>p/2),则点M到准线的距离是__________,点M的横坐标是________.
例3:斜率为1的直线经过y2=4x的焦点,与抛物线相交于两点A、B,求线段AB的长.例4:在抛物线y2=2x上求一点P,使得P到焦点F与到
点A(3,2)的距离之和最小,并求出最小值.Q解: 如图,设|PQ|为P到准线的距离则|PF|=|PQ|∴|AP|+|PF|=|AP|+|PQ|∴当A,P,Q共线时, |AP|+|PF|最小PQ思考:抛物线y2=2px(p>0)的点M到定点A(3,2)和焦点F的距离之和的最小值为5,求抛物线方程小结[1]抛物线的定义(可将两点距离与点线距离的相互转化) [2]标准方程有4种形式,要注意p的几何意义 [3]已知标准方程求焦点坐标或准线方程应先判断后求解 [4]已知焦点坐标或准线方程求抛物线的标准方程也是先判断后求解
