解直角三角形

课件21张PPT。解直角三角形计算器在三角函数方面的使用阅读18页6.3内容，掌握一下要点：
怎样用计算器来求锐角三角函数值？
碰到非整数度数的怎样处理？
怎样用计算器由三角函数值求角？
遇到求锐角的余切值或遇到锐角的余切值求角时，怎么办？
News:从今年起计算器进入中考考场！这意味着什么？比较三角函数值得大小理论依据：角越大，正弦值、正切值越大；
角越大，余弦值、余切值越小。
比较sin55o和cos62o的大小
比较tan87o和cot87o的大小
解直角三角形初步自学21页内容（例1之前的部分），思考：
在直角三角形中，除直角外有哪5个元素？
记住“三边之间关系”、“锐角之间关系”、“边角之间关系”，思考之前我们学习锐角三角函数目的是什么。
解直角三角形的实质是什么？
解直角三角形至少需要知道多少个元素？解直角三角形第一次尝试题
今后，在没有特别说明的情况下，Rt△ABC中，∠C为直角，∠A、∠B、∠C所对的边分别为a、b、c。第一次尝试题研讨：要求的未知元素是哪些？
其中哪个最容易求？
求a可以有什么方法？
求c可以有什么方法？
上述两个问中，比较各种方法的优劣。第一次尝试题研讨：此题解法灵活性很强，你找到了什么方法？
要计算简便，优选关系公式是关键。
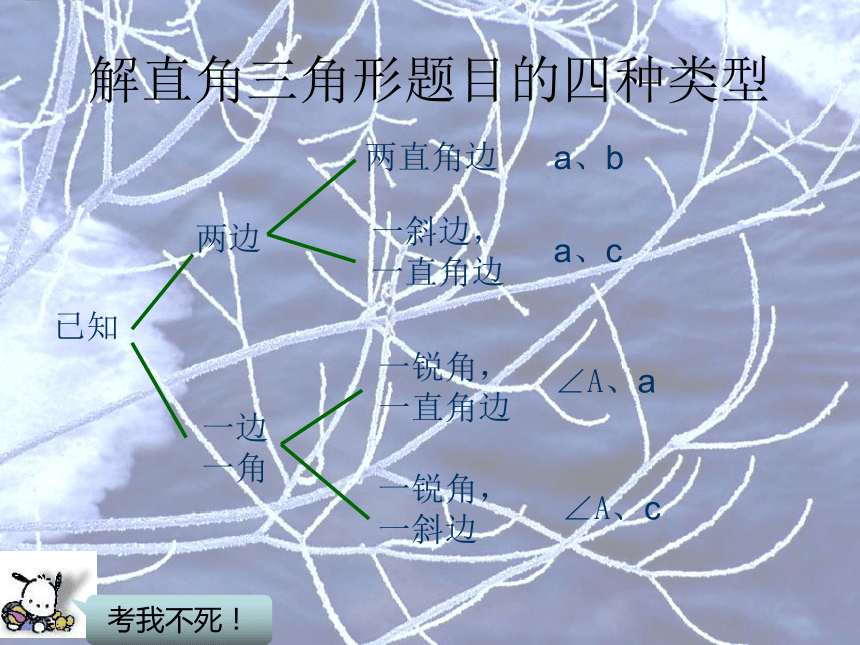
当题目中涉及到的角的度数不是特殊度数时，怎么办？解直角三角形第二次尝试题解直角三角形题目的四种类型已知两边一边一角两直角边一斜边，一直角边一锐角，一直角边一锐角，一斜边a、ba、c∠A、a∠A、c解直应用——人字架问题如图，厂房屋顶人字架（等腰三角形）的跨度为10米，∠A＝26o，求中柱BC（C为底边中点）和上弦AB的长。（精确到0.01米）解直应用——仰角和俯角如图：某飞机于空中A处探测到目标C，此时飞行高度AC＝1200米，从飞机上看第平面控制点B的俯角α＝16o31 ′。求飞机A到控制点B的距离。（精确到1米）解直应用——仰角和俯角如图，线段AB和CD分别表示甲、乙两头座楼的高。AB⊥BD于B，CD⊥BD于D。从甲楼顶部A处测得乙楼顶部C的仰角α＝30o，测得乙楼底部D的俯角β＝60o。已知AB＝24米，求CD＝？解直应用——方位角一艘海轮位于灯塔P的北偏东60o方向上的A处，它沿正南方向航行70海里后，到达位于灯塔P的南偏东30o方向上的B处，这时，海轮所在的B处距离灯塔P有多远？（结果不取近似值）
关键在于：准确画图。解直应用——方位角一个人从A点出发向北偏东60o方向走了一段距离到B点，再从B点出发向南偏西15o方向走了一段距离到C点，则∠ABC的度数是？
两灯塔G和F与海洋观察站O的距离相等，灯塔G在观察站O的北偏东40o，灯塔F在观察站O的南偏东60o，则灯塔G在灯塔F的什么位置？（×偏×？度） 解直应用——斜坡问题在山坡上种树，要求株距（相邻两树间的水平距离）是5.5米，测得斜坡的倾斜角是24o，求斜坡上相邻两树间的坡面距离是多少米（精确到0.1米）。
解直应用——坡度（梯形坝问题）水库大坝的横断面是梯形，坝顶宽6米，坝高23米，斜坡AB的坡度i＝1∶3，斜坡CD的坡度i’＝1∶2.5。求斜坡AB的坡角α，坝底宽AD和斜坡AB的长。（精确到0.1米）解直应用——燕尾槽问题燕尾槽的横断面是等腰梯形。图是一燕尾槽的横断面，其中燕尾角B是55o，外口宽AD是180毫米，燕尾槽的深度是70毫米。求它的里口宽BC。（精确到1毫米）1、要记住相关的名词概念
2、应用题的关键是将实际问题抽象为数学问题（画出平面图，转化为解直角三角形）
3、根据条件的特点，适当选用锐角三角函数的关系式考考你：某型飞机的机翼形状如图所示。根据图中数据计算AC、BD和AB的长度。（保留3个有效数字）作业：28页练习
33页6、7、8、9
△ABC，∠B＝30o，∠ACB＝120o。D是BC上一点，且∠ADC＝45o。若CD＝8。求BD的长。作业：一艘轮船从离A观察站的正北 海里处的B港处向东航行，观察站第一次测得该船在A地北偏东30o的M处；半小时后，又测得该船在A地的北偏东60o的N处。求此船的速度。再见