1.1.2等腰三角形的特殊性质和等边三角形的性质课件(共27张PPT)2023-2024学年度北师大版数学八年级下册
文档属性
| 名称 | 1.1.2等腰三角形的特殊性质和等边三角形的性质课件(共27张PPT)2023-2024学年度北师大版数学八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 333.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 09:53:16 | ||
图片预览







文档简介
(共27张PPT)
1.1.2 等腰三角形的特殊性质和等边三角形的性质
1. 掌握等腰三角形一些特殊线段的性质.
2. 掌握等边三角形的性质.
学习目标
难点
重点
上节课我们证明了等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合. (三线合一)
那等腰三角形的两底角的角平分线、两腰上的高、两腰上的中线有什么关系呢?
新课引入
B
C
A
D
B
C
D
A
E
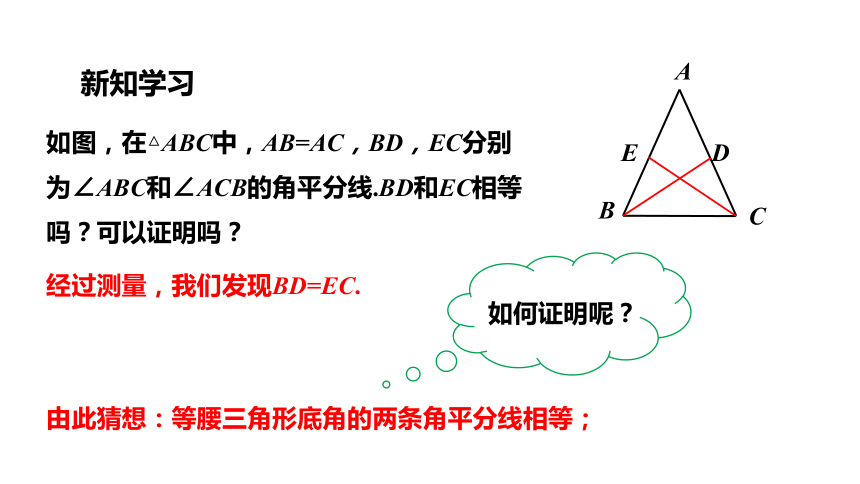
如图,在△ABC中,AB=AC,BD,EC分别为∠ABC和∠ACB的角平分线.BD和EC相等吗?可以证明吗?
经过测量,我们发现BD=EC.
如何证明呢?
由此猜想:等腰三角形底角的两条角平分线相等;
新知学习
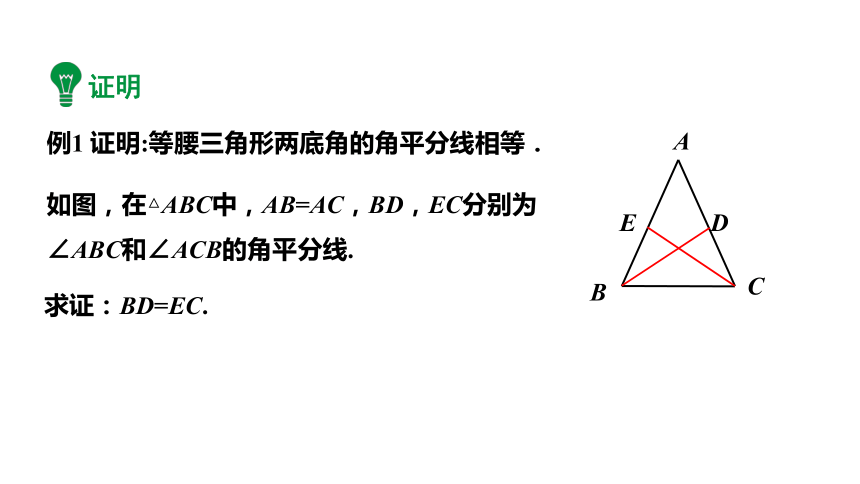
例1 证明:等腰三角形两底角的角平分线相等.
如图,在△ABC中,AB=AC,BD,EC分别为
∠ABC和∠ACB的角平分线.
求证:BD=EC.
B
C
D
A
E
证明
B
C
D
A
E
证明:∵AB=AC,∴∠ABC=∠ACB(等边对等角).
∵∠1= ∠ABC,∠2= ∠ACB,
∴∠1=∠2.
在△BDC和△CEB中,
∵∠ACB=∠ABC,BC=CB,∠1=∠2.
∴△BDC≌△CEB(ASA).
∴BD=CE(全等三角形的对应边相等).
1
2
还有别的证明方法吗?
B
C
D
A
E
3
4
证法二:∵AB=AC,∴∠ABC=∠ACB.
∵∠3= ∠ABC,∠4= ∠ACB,
∴∠3=∠4.
在△ABD和△ACE中,
∵∠3=∠4,AB=AC,∠A=∠A,
∴△ABD≌△ACE( ASA ).
∴BD=CE(全等三角形的对应边相等).
思考
刚才,我们用2种方法证明了等腰三角形中两底角的角平分线相等.
请同学们猜想一下:两腰上的中线、高是否分别相等呢?请你
证明它们.
猜想1:等腰三角形的两腰上的中线相等
猜想2:等腰三角形的两腰上的高相等:
例2 证明: 等腰三角形两腰上的高相等.
B
C
D
A
E
已知:如图3,在△ABC中, AB=AC,
BD,CE是△ABC的高.
求证:BD=CE.
证明
证明:∵AB=AC,∴∠ABC=∠ACB.
∵BD,CE是△ABC的高,
∴∠BDC=∠CEB=90°.
在△BDC和△CEB中,
∵∠BDC=∠CEB,BC=CB,∠ABC=∠ACB,
∴△BDC≌△CEB( AAS ).
∴BD=CE(全等三角形的对应边相等).
B
C
D
A
E
例3 证明:等腰三角形两腰上的中线相等.
B
C
D
A
E
已知:如图,在△ABC中, AB=AC,
BD,CE是△ABC的中线.
求证:BD=CE.
证明
B
C
D
A
E
证明:∵AB=AC,∴∠ABC=∠ACB.
∵BD,CE是△ABC的中线,
∴CD= AC, BE= AB ,即CD=BE.
在△BDC和△CEB中,
∵BC=CB,∠ABC=∠ACB , CD=BE,
∴△BDC≌△CEB( SAS ).
∴BD=CE(全等三角形的对应边相等).
思考
刚刚我们证明了等腰三角形中底角的角平分线、腰上的中线和高分别相等了.
如果是底角的三等分线段呢,相等吗?
同样,腰上的中线的三等分线段、腰上的高的三等分线段呢,相等吗?
探究
如图,在△ABC中,AB =AC,点D,E分别在AC和AB上.
如果∠ABD= ∠ABC,∠ACE= ∠ACB,那么BD=CE吗?
如果∠ABD= ∠ABC,∠ACE= ∠ACB呢?
B
C
D
A
E
由此你能得到一个什么结论?
请同学们用已经学过的定理和基本事实来证明你的猜想.
证明:在△ABC中,AB =AC,
∴∠ABC=ACB
∵∠ABD= ∠ABC,∠ACE= ∠ACB
∴∠ABD=∠ACE
在△ABD和△ACE中
∠ABD=∠ACE,AB =AC,∠A=∠A
∴△ABD≌△ACE(ASA )
∴BD=CE
B
C
D
A
E
证明
归纳
在△ABC中,如果AB =AC,∠ABD= ∠ABC,
∠ACE= ∠ACB,那么BD=CE.
叙述为:
在△ABC中,如果AB=AC,∠ABD=∠ACE,那么BD=CE.
B
C
D
A
E
探究
B
C
D
A
E
如图,在△ABC中,AB =AC,点D,E分别在AC和AB上.
如果AD= AC,AE= AB,那么BD=CE 吗?
如果 AD= AC,AE= AB呢?
由此你能得到什么结论?
我们可不可以类比上面做出猜想呢?
证明你的猜想.
证明:在△ABC中,AB =AC,
∴∠ABC=ACB
∵AD= AC,AE= AB
∴AD=AE
在△ABD和△ACE中
AB =AC,∠A=∠A,AD=AE
∴△ABD≌△ACE(SAS)
∴BD=CE
B
C
D
A
E
证明
归纳
在△ABC中,如果AB=AC,AD= AC,AE= AB,那么BD=CE.
叙述为:
在△ABC中,如果AB=AC,AD=AE,那么BD=CE.
B
C
D
A
E
观察
生活中的很多图形都是等边三角形.
等边三角形是特殊的等腰三角形,那么等边三角形的内角有什么特
征呢
探究
证明:等边三角形三个内角都相等并且每个内角都等于60°.
C
B
A
已知:如图6,在△ABC中,AB=BC=AC.
求证:∠A=∠B=∠C=60°.
证明:在△ABC中,∵AB=AC,
∴∠B=∠C(等边对等角).
同理∠C=∠A,
∴∠A=∠B=∠C(等量代换).
又∵∠A+∠B+∠C=180°(三角形内角和定理).
∴∠A=∠B=∠C=60°.
1.等腰三角形一腰上的高与另一腰的夹角是50°,则这个等腰三角形的底角为( )
A.70° B.20° C.70°或20° D.40°或140°
C
2.已知:等腰三角形的两边长x、y满足方程组 ,
A.5 B.4 C.3 D.5或4
A
2x-y=3
3x+2y=8
则此等腰
三角形的周长为( )
课堂练习
3.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A.BD=CE B.AD=AE
C.DA=DE D.BE=CD
C
4.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
A.30° B.40° C.45° D.36°
B
C
D
A
D
5. 如图,已知△ABC 和△BDE 都是等边三角形,求证:AE = CD.
证明:∵ △ABC 和△BDE 都是等边三角形,
∴AB = BC,∠ABC =∠DBE = 60°,
BE = BD,
∴△ABE ≌△CBD.
∴AE = CD.
A
B
C
D
E
6.如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
解:
∵ △ABC是等边三角形,
∴∠CBA=60°.
∵BD是AC边上的中线,
∴∠BDA=90°,∠DBA=30°.
∵ BD=BE,
∴ ∠BDE=(180 °-∠DBA) ÷2 = (180°-30°) ÷2=75°.
∴ ∠EDA=90 °- ∠BDE=90°-75°=15°.
B
C
D
A
E
这节课你学到了哪些数学知识呢?
1.等腰三角形的特殊性质:
底角的两条平分线相等;
两条腰上的中线相等;
两条腰上的高线相等.
2.等边三角形
定理: 等边三角形的三个内角都相等,并且每个角都等于60°.
课堂小结
1.1.2 等腰三角形的特殊性质和等边三角形的性质
1. 掌握等腰三角形一些特殊线段的性质.
2. 掌握等边三角形的性质.
学习目标
难点
重点
上节课我们证明了等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合. (三线合一)
那等腰三角形的两底角的角平分线、两腰上的高、两腰上的中线有什么关系呢?
新课引入
B
C
A
D
B
C
D
A
E
如图,在△ABC中,AB=AC,BD,EC分别为∠ABC和∠ACB的角平分线.BD和EC相等吗?可以证明吗?
经过测量,我们发现BD=EC.
如何证明呢?
由此猜想:等腰三角形底角的两条角平分线相等;
新知学习
例1 证明:等腰三角形两底角的角平分线相等.
如图,在△ABC中,AB=AC,BD,EC分别为
∠ABC和∠ACB的角平分线.
求证:BD=EC.
B
C
D
A
E
证明
B
C
D
A
E
证明:∵AB=AC,∴∠ABC=∠ACB(等边对等角).
∵∠1= ∠ABC,∠2= ∠ACB,
∴∠1=∠2.
在△BDC和△CEB中,
∵∠ACB=∠ABC,BC=CB,∠1=∠2.
∴△BDC≌△CEB(ASA).
∴BD=CE(全等三角形的对应边相等).
1
2
还有别的证明方法吗?
B
C
D
A
E
3
4
证法二:∵AB=AC,∴∠ABC=∠ACB.
∵∠3= ∠ABC,∠4= ∠ACB,
∴∠3=∠4.
在△ABD和△ACE中,
∵∠3=∠4,AB=AC,∠A=∠A,
∴△ABD≌△ACE( ASA ).
∴BD=CE(全等三角形的对应边相等).
思考
刚才,我们用2种方法证明了等腰三角形中两底角的角平分线相等.
请同学们猜想一下:两腰上的中线、高是否分别相等呢?请你
证明它们.
猜想1:等腰三角形的两腰上的中线相等
猜想2:等腰三角形的两腰上的高相等:
例2 证明: 等腰三角形两腰上的高相等.
B
C
D
A
E
已知:如图3,在△ABC中, AB=AC,
BD,CE是△ABC的高.
求证:BD=CE.
证明
证明:∵AB=AC,∴∠ABC=∠ACB.
∵BD,CE是△ABC的高,
∴∠BDC=∠CEB=90°.
在△BDC和△CEB中,
∵∠BDC=∠CEB,BC=CB,∠ABC=∠ACB,
∴△BDC≌△CEB( AAS ).
∴BD=CE(全等三角形的对应边相等).
B
C
D
A
E
例3 证明:等腰三角形两腰上的中线相等.
B
C
D
A
E
已知:如图,在△ABC中, AB=AC,
BD,CE是△ABC的中线.
求证:BD=CE.
证明
B
C
D
A
E
证明:∵AB=AC,∴∠ABC=∠ACB.
∵BD,CE是△ABC的中线,
∴CD= AC, BE= AB ,即CD=BE.
在△BDC和△CEB中,
∵BC=CB,∠ABC=∠ACB , CD=BE,
∴△BDC≌△CEB( SAS ).
∴BD=CE(全等三角形的对应边相等).
思考
刚刚我们证明了等腰三角形中底角的角平分线、腰上的中线和高分别相等了.
如果是底角的三等分线段呢,相等吗?
同样,腰上的中线的三等分线段、腰上的高的三等分线段呢,相等吗?
探究
如图,在△ABC中,AB =AC,点D,E分别在AC和AB上.
如果∠ABD= ∠ABC,∠ACE= ∠ACB,那么BD=CE吗?
如果∠ABD= ∠ABC,∠ACE= ∠ACB呢?
B
C
D
A
E
由此你能得到一个什么结论?
请同学们用已经学过的定理和基本事实来证明你的猜想.
证明:在△ABC中,AB =AC,
∴∠ABC=ACB
∵∠ABD= ∠ABC,∠ACE= ∠ACB
∴∠ABD=∠ACE
在△ABD和△ACE中
∠ABD=∠ACE,AB =AC,∠A=∠A
∴△ABD≌△ACE(ASA )
∴BD=CE
B
C
D
A
E
证明
归纳
在△ABC中,如果AB =AC,∠ABD= ∠ABC,
∠ACE= ∠ACB,那么BD=CE.
叙述为:
在△ABC中,如果AB=AC,∠ABD=∠ACE,那么BD=CE.
B
C
D
A
E
探究
B
C
D
A
E
如图,在△ABC中,AB =AC,点D,E分别在AC和AB上.
如果AD= AC,AE= AB,那么BD=CE 吗?
如果 AD= AC,AE= AB呢?
由此你能得到什么结论?
我们可不可以类比上面做出猜想呢?
证明你的猜想.
证明:在△ABC中,AB =AC,
∴∠ABC=ACB
∵AD= AC,AE= AB
∴AD=AE
在△ABD和△ACE中
AB =AC,∠A=∠A,AD=AE
∴△ABD≌△ACE(SAS)
∴BD=CE
B
C
D
A
E
证明
归纳
在△ABC中,如果AB=AC,AD= AC,AE= AB,那么BD=CE.
叙述为:
在△ABC中,如果AB=AC,AD=AE,那么BD=CE.
B
C
D
A
E
观察
生活中的很多图形都是等边三角形.
等边三角形是特殊的等腰三角形,那么等边三角形的内角有什么特
征呢
探究
证明:等边三角形三个内角都相等并且每个内角都等于60°.
C
B
A
已知:如图6,在△ABC中,AB=BC=AC.
求证:∠A=∠B=∠C=60°.
证明:在△ABC中,∵AB=AC,
∴∠B=∠C(等边对等角).
同理∠C=∠A,
∴∠A=∠B=∠C(等量代换).
又∵∠A+∠B+∠C=180°(三角形内角和定理).
∴∠A=∠B=∠C=60°.
1.等腰三角形一腰上的高与另一腰的夹角是50°,则这个等腰三角形的底角为( )
A.70° B.20° C.70°或20° D.40°或140°
C
2.已知:等腰三角形的两边长x、y满足方程组 ,
A.5 B.4 C.3 D.5或4
A
2x-y=3
3x+2y=8
则此等腰
三角形的周长为( )
课堂练习
3.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A.BD=CE B.AD=AE
C.DA=DE D.BE=CD
C
4.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
A.30° B.40° C.45° D.36°
B
C
D
A
D
5. 如图,已知△ABC 和△BDE 都是等边三角形,求证:AE = CD.
证明:∵ △ABC 和△BDE 都是等边三角形,
∴AB = BC,∠ABC =∠DBE = 60°,
BE = BD,
∴△ABE ≌△CBD.
∴AE = CD.
A
B
C
D
E
6.如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
解:
∵ △ABC是等边三角形,
∴∠CBA=60°.
∵BD是AC边上的中线,
∴∠BDA=90°,∠DBA=30°.
∵ BD=BE,
∴ ∠BDE=(180 °-∠DBA) ÷2 = (180°-30°) ÷2=75°.
∴ ∠EDA=90 °- ∠BDE=90°-75°=15°.
B
C
D
A
E
这节课你学到了哪些数学知识呢?
1.等腰三角形的特殊性质:
底角的两条平分线相等;
两条腰上的中线相等;
两条腰上的高线相等.
2.等边三角形
定理: 等边三角形的三个内角都相等,并且每个角都等于60°.
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
