锐角三角函数(4)
图片预览








文档简介
课件21张PPT。28.1锐角三角函数(4)复习: 1.锐角三角函数的定义: ∠A的余弦 :∠A的正弦:互余两角之间的三角函数关系:同角之间的三角函数关系:特殊角300,450,600角的三角函数值.2.性质: ◆范围:00sinA=cosB,tanA●tanB=1.sin2A+cos2A=1. 3.我们学习了30°, 45°, 60°这几类特殊角的三角函数值: 例1:(2)已知: α为一锐角, tanα =0.5 ,
求sin α,cos α的值.(1)已知: α为一锐角,且sin(α-15°) = ,
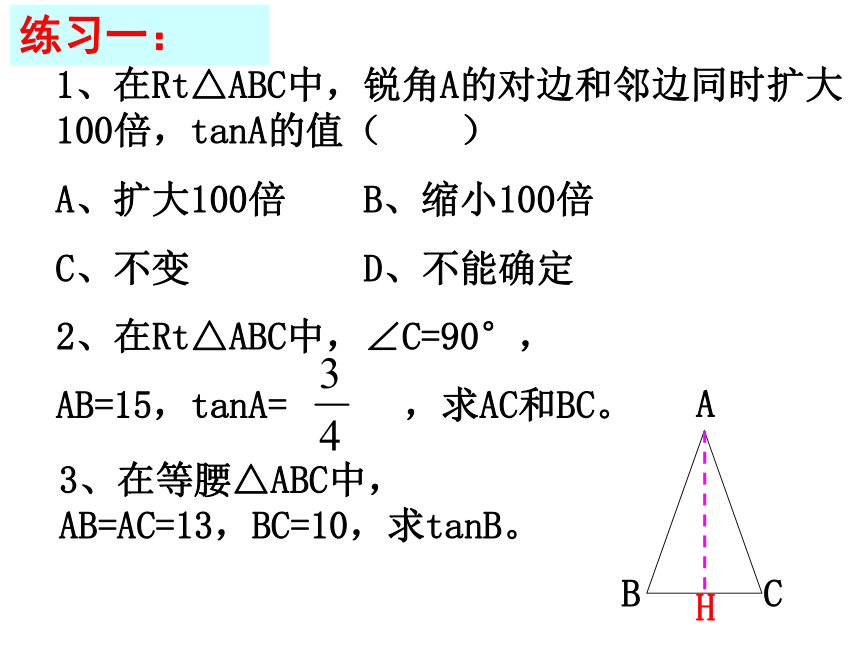
求cos α , tanα的值.k2k1、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A、扩大100倍 B、缩小100倍
C、不变 D、不能确定练习一:3、在等腰△ABC中,AB=AC=13,BC=10,求tanB。5、在Rt△ABC中,∠C=90°,化简(∠ A <45°)
(4)4、计算:1050则锐角∠A的取值范围是多少?1. 当 锐角A>45°时,sinA的值( )B2. 当锐角A>30°时,cosA的值( )C练习二:3. 若cosA>0.5时,则sinA的取值范围是 .例3:在△ABC中,D是AB的中点,DC⊥AC,tan∠BCD=0.5,AB=4 ,求AC。H1、Rt△BAC中,∠C=900,CA=CB
D是AC上一点,且DA= AC,求∠ABD的三个三角函数值。练习三:2、如图,在△ABC中, AB=BC=5,sinA=4/5,求△ABC 的面积。3、在平面直角坐标系中,有一条直线l:y=5/12x,l与x轴的正半轴的夹角为α,求sinα的值。D4.△ABC中,AB=8,BC=6,S△ABC=12,试求sinB的值.D7. 如图,在RT△ABC中,∠C=900,若tanA+tanB=4,S△ABC=8.求斜边AB的长.8. 如图,△ABC中,∠C=900,BD平分∠ABC,BC=12,BD= ,求∠A的度数及AD的长.例4.如图,身高1.5m的小丽用一个两锐角分别是300和600 的三角尺测量一棵树的高度.已知她与树之间的距离为5m,那么这棵树大约有多高? 操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1.65米.然后他很快就算出旗杆的高度了。1.65米10米? 你想知道小明怎样算出的吗?30°练习四:练习五:中考链接:1.(安徽)如图是五角星,已知AC=a,求五角星外接圆的直径(结果用三角函数表示)4.(济南)某班布置会场时,需用直角三角形彩纸裁剪成长度不等的矩形彩条,如图,在Rt△ABC中,∠C=90o,AC=30cm, AB=50cm,依次裁下宽为1cm的矩形纸条a1、a2、a3…,若使裁下的矩形纸条的长都不少于5cm,则每张直角三角形彩纸能裁成的矩形纸条的总数是_______条.5.(浙江)身高相等的三名同学甲、乙、丙参加风筝比赛,三人放出的风筝线长、线与地面的夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )
A)甲的最高 B)丙的最高
C)乙的最低 D)丙的最低
求sin α,cos α的值.(1)已知: α为一锐角,且sin(α-15°) = ,
求cos α , tanα的值.k2k1、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A、扩大100倍 B、缩小100倍
C、不变 D、不能确定练习一:3、在等腰△ABC中,AB=AC=13,BC=10,求tanB。5、在Rt△ABC中,∠C=90°,化简(∠ A <45°)
(4)4、计算:1050则锐角∠A的取值范围是多少?1. 当 锐角A>45°时,sinA的值( )B2. 当锐角A>30°时,cosA的值( )C练习二:3. 若cosA>0.5时,则sinA的取值范围是 .例3:在△ABC中,D是AB的中点,DC⊥AC,tan∠BCD=0.5,AB=4 ,求AC。H1、Rt△BAC中,∠C=900,CA=CB
D是AC上一点,且DA= AC,求∠ABD的三个三角函数值。练习三:2、如图,在△ABC中, AB=BC=5,sinA=4/5,求△ABC 的面积。3、在平面直角坐标系中,有一条直线l:y=5/12x,l与x轴的正半轴的夹角为α,求sinα的值。D4.△ABC中,AB=8,BC=6,S△ABC=12,试求sinB的值.D7. 如图,在RT△ABC中,∠C=900,若tanA+tanB=4,S△ABC=8.求斜边AB的长.8. 如图,△ABC中,∠C=900,BD平分∠ABC,BC=12,BD= ,求∠A的度数及AD的长.例4.如图,身高1.5m的小丽用一个两锐角分别是300和600 的三角尺测量一棵树的高度.已知她与树之间的距离为5m,那么这棵树大约有多高? 操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1.65米.然后他很快就算出旗杆的高度了。1.65米10米? 你想知道小明怎样算出的吗?30°练习四:练习五:中考链接:1.(安徽)如图是五角星,已知AC=a,求五角星外接圆的直径(结果用三角函数表示)4.(济南)某班布置会场时,需用直角三角形彩纸裁剪成长度不等的矩形彩条,如图,在Rt△ABC中,∠C=90o,AC=30cm, AB=50cm,依次裁下宽为1cm的矩形纸条a1、a2、a3…,若使裁下的矩形纸条的长都不少于5cm,则每张直角三角形彩纸能裁成的矩形纸条的总数是_______条.5.(浙江)身高相等的三名同学甲、乙、丙参加风筝比赛,三人放出的风筝线长、线与地面的夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )
A)甲的最高 B)丙的最高
C)乙的最低 D)丙的最低
