河北基教考试中心2009年2月高考数学研讨会
文档属性
| 名称 | 河北基教考试中心2009年2月高考数学研讨会 |  | |
| 格式 | rar | ||
| 文件大小 | 511.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-16 19:33:00 | ||
图片预览










文档简介
课件123张PPT。2009年高考考试大纲解读 及高考备考策略北京工大附中 常毓喜
河北基教考试研究中心
高考研讨会 第一部分:2009年高考考试大纲解读第二部分:高考备考策略①把《2008年普通高等学校招生全国统一考试大纲》变为《普通高等学校招生全国统一考试大纲(2009年版)》;
②Ⅳ.考试形式与试卷结构:把“试卷应由容易题、中等题和难题组成,总体难度要适当,并以中等题为主”改为“试卷应由容易题、中等难度题和难题组成,总体难度要适当,并以中等难度题为主”.第一部分:2009年高考考试大纲解读③前言中,删去了下面两段话:
题型是呈现考试内容的形式.不同的题型,在考查不同知识、能力及其层次上有不同的功能.因此,《考试大纲》根据考试内容也提出了相应的题型.
在总结2007年命题经验和考情况的基础上,作了适当修订,以便更好的适应高校招生需要和中学教学实际,力求对中学全面实施素质教育发挥积极的作用.●考试性质
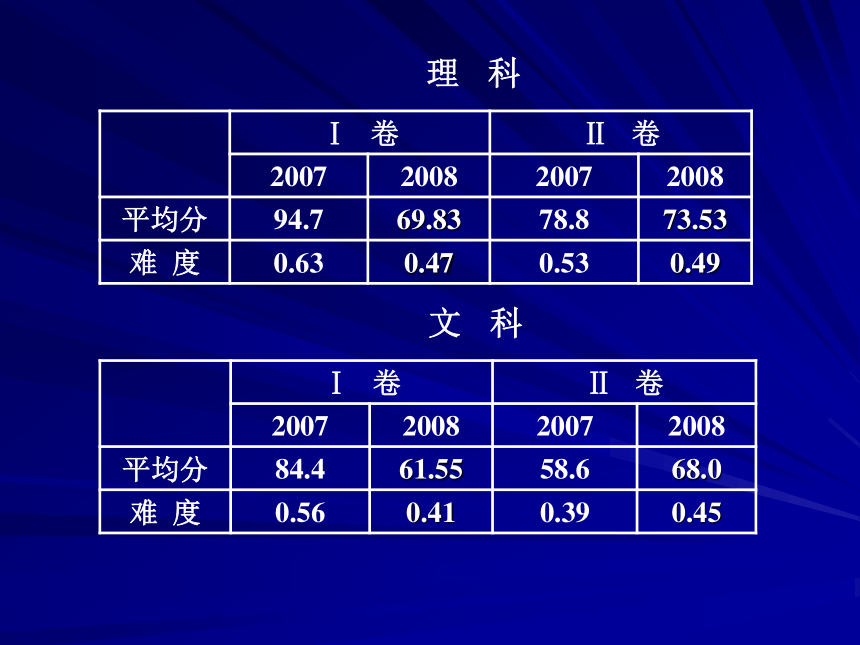
普通高等学校招生全国统一考试是合格的高中毕业生和具有同等学力的考生参加的选拔性考试.高等学校根据考生成绩,按已确定的招生计划,德、智、体全面衡量,择优录取.因此,高考应具有较高的信度、效度,必要的区分度和适当的难度.理 科文 科●考试要求一、命题原则
数学科的考试,按照“考查基础知识的同时,注重考查能力”的原则,确立以能力立意命题的指导思想,将知识、能力和素质融为一体,全面检测考生的数学素养.
数学科考试要发挥数学作为基础学科的作用,既考查中学数学的知识和方法,又要考查考生进入高校继续学习的潜能.(2007年北京卷理19题)如图,有一块半椭圆形钢板,其长半轴为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.
(I)求面积S以为自变量x的函数式,并写出其定义域;
(II)求面积S的最大值.二、考试要求1.知识要求
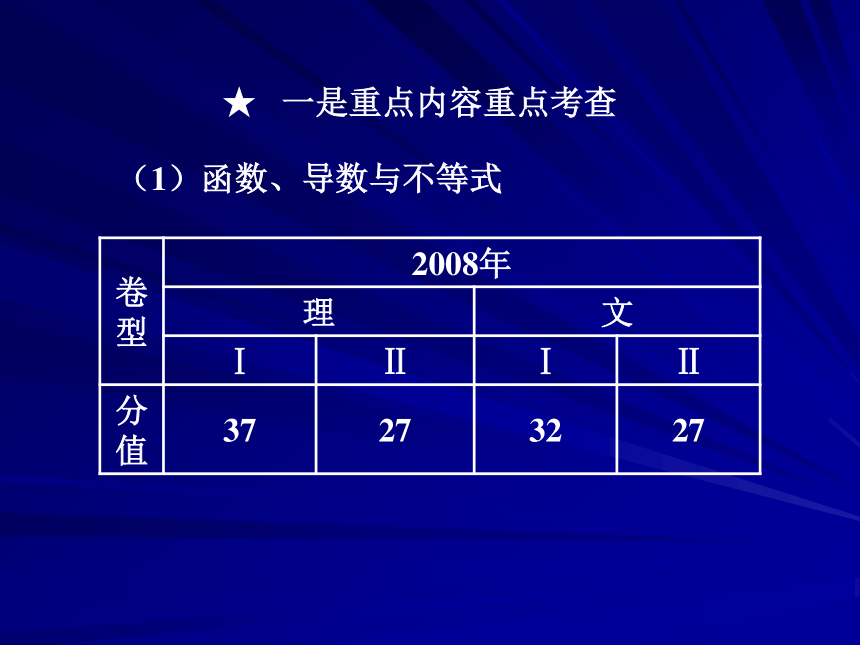
对数学基础知识的考查,要既全面又突出重点,对于支撑学科知识体系的重点内容,要占有较大的比例,构成数学试卷的主体.注重学科的内在联系和知识的综合性,不刻意追求知识的覆盖面.从学科的整体高度和思维价值的高度考虑问题,在知识网络交汇点设计试题,使对数学基础知识的考查达到必要的深度.★ 一是重点内容重点考查(1)函数、导数与不等式(2008年全国Ⅱ卷理第22题)
设函数
(Ⅰ)求f(x)的单调区间;
(Ⅱ)如果对任何x≥0,都有f(x)≤ax,求a的取值范围.(2)数列(2008年全国Ⅱ卷理第22题) 设函数 f(x) =x-xlnx.数列{an}满足0(Ⅰ)证明:函数f(x)在区间(0,1)是增函数;
(Ⅱ)证明:an< an+1<1;
(Ⅲ)设b∈(a1,1),整数 证明:ak+1>b.(3)三角函数 (2008年全国Ⅰ卷理科第17题)设△ABC的内角A,B,C所对的边长分别为a,b,c,
且
(Ⅰ)求tanAcotB的值;
(Ⅱ)求tan(A-B)的最大值. 解(Ⅰ) 即 展开并整理得: 所以tanAcotB=4. (Ⅱ) 由(Ⅰ)得:tanA=4tanB. 当且仅当(4)立体几何(2007年Ⅱ卷理第19题)在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点.
(1)证明EF∥平面SAD;
(2)设SD=2DC,求二面角A-EF-D的大小.(2)解法一:不妨设DC=2,
则SD=4,DG=2 .ASBCDEFGH取AG的中点H,连结DH,则DH⊥AG.又AB⊥平面SAD,所以
AB ⊥DH,从而
DH⊥平面 AEF.ASBCDEFGMH取EF的中点M,连结MH,则
MH⊥EF.连结DM,HM,则MH⊥EF.故∠DMH为二面角A-EF-D的平面角.所以二面角A-EF-D的大小为解法二:取DS的中点为G,
DC的中点为H,连结AG,
FG,FH,EH,ASBCDEFGMH则三棱柱AGD-EFH为直三棱柱。取EF的中点为M,连结DM,
HM,则∠DMH为二面角A-EF-D的余角.(2007年Ⅰ卷理第19题)四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2 ,SA=SB=
(Ⅰ)证明SA⊥BC;
(Ⅱ)求直线SD与平面SAB所成角的大小.SABCDO(5)解析几何(2008年全国Ⅰ卷理第21题)双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于两点A,B.已知|OA|,|AB|,|OB|成等差数列,且 与 同向.
(Ⅰ)求双曲线的离心率;
(Ⅱ)设AB被双曲线所截得的线段的长为4,求双曲线的方程.解法一:设出渐近线与直线AB的方程,然后求出A,B两点坐标,再利用|OA|,|AB|,|OB|成等差数列得到a与b的关系,最后求出离心率.解法二:由|OA|,|AB|,|OB|成等差数列及勾股定理得到4|OA|=3|AB|,所以然后即可得到a与b的关系,最后求出离心率.解法三、 |FA|= b,所以|OA|=a.设|OB|=n,|FB|=q,则 (6)概率与统计(2008年全国Ⅰ卷理第20题)已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性的即没患病.下面是两种化验方法:
方案甲:逐个化验,直到能确定患病动物为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
(Ⅰ)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;
(Ⅱ)?表示依方案乙所需化验次数,求? 的期望.分析: (Ⅰ)设依方案甲所需化验次数为?,则?的所有可能取值为1,2,3,4. 设依方案乙所需化验次数为?,则?的所有可能取值为2,3. 当?=2时,要分两种情况:将3只血液混在一起化验的结果呈阳性与将3只血液混在一起化验的结果呈阴性,所以甲乙则依方案甲所需化验次数不少于依方案乙所需化验次数包括“?=2,且?=2”、“? =3,且? =2或? =3” 与“? =4,且? =2或? =3”,它们是彼此互斥事件,所以依方案甲所需化验次数不少于依方案乙所需化验次数的概率为(Ⅱ)E?=2×0.6+3×0.4=2.4,即依方案乙所需化验次数?的期望为2.4.★二是加强知识的综合性 (2007年Ⅰ卷第12题)(难度系数:0.466)
函数 的一个单调增区间是★三是对基础知识的考查要达到必要的深度解法一:解法二: 解法三:由柯西不等式得:解法四: 由m?n≤|m|?|n|得: 解法五: 直线 通过点M(cos?,sin?),则整理得: a2+b2≥a2b2,所以解法六:如图,由图1可以排除A选项,由图2可以排除B、C选项,所以应该选D。xya11图1xyba图2b11(2008年全国Ⅰ卷理第14题)(难度系数0.316)已知抛物线y=ax2-1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 .(2008年全国Ⅰ卷理第16题)(难度系数0.075)等边三角形ABC与正方形ABDE有一公共边AB,二面角C-AB-D的余弦值为 ,M,N分别是AC,BC的中点,则EM,AN所成角的余弦值等于 . 对数学思想和方法的考查是对数学知识在更高层次上的抽象和概括的考查,考查时必须要与数学知识相结合,通过数学知识的考查,反映考生对数学思想和方法的理解;要从学科整体意义和思想价值立意,注意通性通法,淡化特殊技巧,有效地检测考生对中学数学知识中所蕴涵的数学思想和方法的掌握程度.(2007年Ⅰ卷理17题文第20题)设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA.
(Ⅰ)求B的大小;
(Ⅱ)求cosA+sinC的取值范围.函数的思想解:(Ⅰ)根据正弦定理得sinA=2sinBsinA,(Ⅱ)方程的思想数形结合的思想(2005年全国Ⅰ卷理科第12题)
过三棱柱任意两个顶点的直线共15条,其中异面直线有
(A)18对
(B)24对
(C)30对
(D)36对分类讨论的思想转化与化归的思想ABCDEFGMNGMNO(H)特殊与一般的思想(全国甲卷文理科第4题)设三棱柱ABC-A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,则四棱锥B-APQC的体积为
(A)
(B)
(C)
(D)xyPQFO有限与无限的思想 一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜。记三种盖法屋顶面积分别为p1、p2、p3. ① ② ③
若屋顶斜面与水平面所成的角都是?,则(2001年全国新课程理科第11题)2.能力要求
对数学能力的考查,强调 “以能力立意”,就是以数学知识为载体,从问题入手,把握学科的整体意义,用统一的数学观点组织材料,侧重体现对知识的理解和应用,尤其是综合和灵活的应用,以此来检测考生将知识迁移到不同情景中去的能力,从而检测出考生个体理性思维的广度和深度以及进一步学习的潜能. (1)思维能力
对能力的考查,以思维能力为核心,全面考查各种能力,强调综合性、应用性,并切合考生实际. (2006年北京卷理文8题)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口 A、B、 C 的机动车辆数如图所示,图中 x1, x2, x3分别表示该时段单位时间通过路段 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则 (A)x1>x2>x3 ? ? (B)x1> x3 > x2
(C)x2 > x3> x1? (D)x3 > x2> x1(2007年广东卷第7题)图3是某汽车维修公司的维修点环形分布图,公司在年初分配给A、B、C、D四个维修点某种配件各50件.在使用前发现需将A、B、C、D四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进行.那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为
A.18 B.17 C.16 D.15方案一:从A往D调动10件,从C往D调动1件,从B往C调动5件;方案二:从A往D调动11件,从B往A调动1件,从B往C调动4件; 设这四个维修点A,B,C,D处的调动件数分别为xA,xB, xCxD,则有xA≥|50-40|=10, xB≥|50-45|=5,
xC≥|50-54|=4, xD≥|50-61|=11,所以总的调动件数n不小于不相邻的维修点之间调动件数之和,即n≥14且n≥16.y=|x1|+|x2|+|x3|+|x4|=|x1|+|x1+5|+|x1+1|+|x1-10|≥|(x1-10)-(x1+5)|+|(x1+1)-x1|=11+5=16, 当(x1-10)(x1+5)≤0且x1(x1+1)≤0
时等号成立,这时0≤x1≤ -1. (2006年全国甲卷理12题)A.190 B.171
C.90 D.45方法一: 第一个等号当9≤x≤11时取到,第二个等号当x=10时取到,所以当x=10时f(x)取到最小值90.方法二:利用绝对值的性质,则有f(x)=|x-1|+|x-2|+???+|x-9|+|x-10|+|x-11|+???+|x-19|≥|x-1+x-2+???+x-9+11-x+???+19-x|+|x-10|=90+|x-10|≥90.方法三:利用绝对值的性质,则有|x-1|+|x-19|≥19-1=18,等号当1≤x≤19时取到;|x-2|+|x-18|≥18-2=16,等号当2≤x≤18时取到;|x-3|+|x-17|≥17-3=14 ,等号当3≤x≤17时取到;… …|x-9|+|x-11|≥11-9=2 ,等号当9≤x≤11时取到;|x-10|≥0 ,等号当x=10时取到;所以当x=10时f(x)取到最小值为 18+16+14+…+2=90. 对运算能力的考查主要是对算理和逻辑推理的考查,考查时以代数运算为主,同时也考查估算、简算.(2)运算能力如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF∥AB,EF,EF与面AC的距离为2,则该多面体的体积为(1999年全国卷理10题)ABEFCD明显VABCDEF>VE-ABCD =6,所以可以排除A、B、C,故D正确. 对空间想象能力的考查,主要体现在对文字语言、符号语言及图形语言三种语言的互相转化,表现为对图形的识别、理解和加工,考查时要与运算能力、逻辑思维能力相结合.(3)空间想象能力(2007年海宁卷理第8题)已知某个几何体的 三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是20 正视图侧视图10俯视图20 20 10(2007年海宁卷理第12题)一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为h1,h2 ,h3,则h1:h2 :h3=一、高考复习的基本经验
1.总体安排
第一轮:9月至第二年3月
——基础知识过关(逐章复习);
第二轮:3月至5月初
——综合能力突破(专题复习);
第三轮:5月初至5月底
——综合能力提升(查缺补漏).第二部分:高考备考策略二、高考复习的几个误区(1)高考试题的一个重要来源就是课本1.以复习资料为纲,偏离课本(2)基本概念的定义应以课本为准(3)基本方法的一个重要来源就是课本(4)解题格式的规范标准来源于课本(课本第三册第一章复习参考题B组第2题)在一个单位普查某种疾病,1000个人去验血,对这些人的血的化验可以用两种方法进行:
(Ⅰ)每个人的血分别化验,这时需要化验1000次;
(Ⅱ)把每个人的血样分成两份,取k个人的血样各一份混在一起进行,如果结果是阴性的,那么对这k个人只作一次检验就够了;如果结果是阳性的,那么再对这k个人的另一份血样逐个化验,这时对这k个人共需作k+1次化验.
假定对所有人来说,化验结果是阳性的概率是0.1,而且这些人的反映是独立的,试比较两种方法所需化验次数的多少.对此问题作一般化的讨论.(1)高考试题的一个重要来源就是课本(2005年湖北理第19题)某地最近出台一项机动车驾照考试规定;每位考试者一年之内最多有4次参加考试的机会,一旦某次考试通过,使可领取驾照,不再参加以后的考试,否则就一直考到第4次为止.如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9,求在一年内李明参加驾照考试次数?的分布列和?的期望,并求李明在一年内领到驾照的概率.(课本1.2离散型随机变量的期望与方差的例3)有一批数量很大的产品,其次品率为15%,对这批产品进行抽查,每次抽出1件,如果抽出次品,则终止抽查,否则继续抽查,直到抽出次品,但抽查次数最多不超过10次,求抽取次数的期望.(2)基本概念的定义应以课本为准(2004年湖北理第16题)某日中午12时整,甲船自A处以16km/h的速度向正东行驶,乙船自A的正北18km处以24km/h的速度向正南行驶,则当日12时30分时两船之间距离对时间的变化率是 km/h.(2008年北京卷理第12题) 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为 (0,4), (2,0), (6,4),则f(f(0)= ;
(用数字作答)C yx1234562134BA(2008年全国Ⅱ卷理科第16题)平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:
充要条件① ;
充要条件② .
(写出你认为正确的两个充要条件)例:写出p且q形式的复合命题
p:邻边相等的平行四边形是正方形;
q:邻边互相垂直的平行四边形是正方形;p且q的复合命题:
邻边相等且邻边互相垂直的平行四边形是正方形; 邻边相等的平行四边形是正方形且邻边互相垂直的平行四边形是正方形.例:命题p :“若(x-1)(x-2)=0,则x =1”的否定是 .【例】写出下列命题的否定:
(1)2是偶数;
(2)奇数是质数;
(3)菱形的对角线相等.错解:若(x-1)(x-2)=0,则x≠1;正解:存在x∈R,(x-1)(x-2)=0,且x≠1.(2007年山东卷文理第7题)命题“对任意的x∈R, x3-x2+1≤0”的否定是
A.不存在x∈R, x3-x2+1≤0
B.存在x∈R, x3-x2+1≤0
C.存在x∈R, x3-x2+1>0
D.对任意的x∈R, x3-x2+1>0 【例】由0到9这10个数字可以组成多少个从左到右恰好是从大到小排列的三位数?【例】5个人排成一排,要求A必须在B的右边(可以不相邻),有多少种不同的排法?(3)基本方法的一个重要来源就是课本(2007年山东卷理第17题)设数列{an}满足,
(1)求数列{an}的通项;
(2)设 求数列{bn}的前n项和Sn.(2008年全国Ⅱ卷)设数列{an}的前n项和为Sn,已知a1=a, an+1=Sn+3n (n∈N*) ,设bn=Sn-3n ,求数列{bn}的通项.解法一:由 an+1=Sn+3n 得: an=Sn-1+3n-1 ,两式相减得:两边都相减去2?3n得:所以数列{an-2?3n-1}是以a-2为首项,以2为公比的等比数列,故解法二:由 an+1=Sn+3n 得: Sn+1-Sn=Sn+3n,即两边都相减去3n+1得:所以数列{Sn-3n}是以a-3为首项,以2为公比的等比数列,故由 an+1=Sn+3n 得: an=Sn-1+3n-1 ,解法一解法二 Sn+1-Sn=Sn+3n,由 an+1=Sn+3n 得:(4)解题格式的规范标准来源于课本2.不重视对考试大纲与高考试题的研究《考试大纲》的要求:了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项.①递推数列: (2004年Ⅲ卷理科第15题)
已知数列{an}满足a1=1,an = a1+2a2+…
+(n-1) an-1(n≥2),则它的通项公式(2007年全国Ⅱ卷理第21题)设数列{an}的首项
a1∈(0,1),
(1)求{an}的通项公式;
(2)设 ,证明bn< bn+1 ,其中n为正整数.(2007年全国Ⅰ卷理22题)已知数列{an}中,a1=2,
(Ⅰ)求{an}的通项公式;
(Ⅱ)若数列{bn}中,
证明:(2008年全国Ⅱ卷)设数列{an}的前n项和为Sn, 已知a1=a, an+1=Sn+3n (n∈N*) .
(Ⅰ)设bn=Sn-3n ,求数列{bn}的通项;
(Ⅱ)若an+1 ≥an, n∈N*,求a的取值范围.②数列求和:
《考试大纲》与《教学大纲》中没有明确的考查要求,但在高考中却有一般数列的求和问题.设正项等比数列{an}的首项a1= ,前n项和为Sn,且210S30-(210+1)S20+S10=0.
(Ⅰ)求{an}的通项;
(Ⅱ)求{nSn}的前n项和Tn.(2005年全国Ⅰ卷文21题)(2007年全国乙卷文第22题)设{an}是等差数列, {bn}是各项都为正数的等比数列,且a1=b1=1, a3+b5=21, a5+b3=13 .
(Ⅰ)求{an} , {bn}的通项公式;
(Ⅱ)求数列 的前n项和Sn . ③概率与统计
考试要求
(1)了解随机变量、离散型随机变量的意义,会求出某些简单的离散型随机变量的分布列.
(2)了解离散型随机变量的期望值、方差的意义,会根据离散型随机变量的分布列求出期望值、方差.
(3)会用抽机抽样,系统抽样,分层抽样等常用的抽样方法从总体中抽取样本.
(4)会用样本频率分布去估计总体分布.
(5)了解正态分布的意义及主要性质.
(6)了解线性回归的方法和简单应用. 这一层次所涉及的主要行为动词有:了解,知道、识别、模仿,会求、会解等. 了解:要求对所列知识的含义有初步的、感性的认识,知道这一知识内容是什么,按照一定的程序和步骤照样模仿,并能(或会)在有关的问题中识别和认识它. 在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布N(70,100).已知成绩在90分以上(含90分)的学生有12名.
(Ⅰ)试问此次参赛学生总数约为多少人?
(Ⅱ)若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?
可共查阅的(部分)标准正态分布表Ф(X0)=P(x0).若ξ在(0,1)内取值的概率为0.4,则在(0,2)内取值的概率为 .(2007年浙江理第5题)已知随机变量ξ服从正态分布N(2,?2),,则P(ξ≤0)=
A.0.16 B.0.32 C.0.68 D. 0.84 (2007年湖南理第5题)设随机变量ξ服从标准 正态分布N(0,1),已知Φ(-1.96)=0.025,则P(|ξ|<1.96)=( )
A.0.025 B.0.050 C.0.950 D.0.975(2008年安徽卷第10题)设两个正态分布N(?1,?1) (?1>0)和N(?2,?2) (?2>0)的密度函数图像如图所示.则有
A. ?1?2
C. ?1>?2, ?1?2, ?1>?2 (2008年湖南卷第4题)设随机变量?服从正态分布N(2,9),若P(?>c+1)=P(? A.1 B.2 C.3 D.4 (2008年重庆卷第5题)已知随机变量?服从正态分布N(3,a2),则P(?<3)=
(A) (B) (C) (D)(2007年广东卷理17题)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y (吨标准煤)的几组对照数据
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y = x+a;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)1.关于专题的选择三、最后阶段的复习(1)高考的重点与热点;
(2)学习中的难点;
(3)数学思想方法;
(4)选择题填空题等的答题技巧;1.函数与导数;
2.数列;
3.三角函数;
4.立体几何;
5.解析几何;
6.概率与统计.1.数学思想方法;
2.选择题的求解策略;
3.填空题的求解策略;
4.基本解答题的求解策略;
5.综合题的求解策略; 应注意的问题
①突出主干知识和重点,抓大放小;
选择适当的专题,引导学生对知识体系进行自主构建,突出重点内容,设置适量问题,这是对专题知识部分的基本要求.忌讳专题选择过多,设置问题过多.②注重对相关问题的整合,减轻学生负担,提高课堂效益.
学生普遍反感和憎恨的事情,就是作业太多.让学生无奈的是有些习题教师也没有经过精选,甚至出现整套题下发、重复题出现,白白浪费了学生宝贵的时间. 2.关于模拟练习
(1)30分钟卷:8道选择题,2道填空题;
(2)45分钟卷:8道选择题,2道填空题,2道解答题;
(3)100分钟卷:10道选择题,3道填空题,5道解答题;
(4)120分钟卷:12道选择题,4道填空题,6道解答题;3.关于试卷讲评
(1)讲试题的背景及考查重点;
(2)讲试题的解答思路与思维历程;
(3)讲学生的作答情况,主要是存在的问题;
(4)讲试题的拓展、变式等.4.关于最后阶段的复习
自主复习、查漏补缺、回归课本、注重基础、树立信心谢 谢
2009.2.14
河北基教考试研究中心
高考研讨会 第一部分:2009年高考考试大纲解读第二部分:高考备考策略①把《2008年普通高等学校招生全国统一考试大纲》变为《普通高等学校招生全国统一考试大纲(2009年版)》;
②Ⅳ.考试形式与试卷结构:把“试卷应由容易题、中等题和难题组成,总体难度要适当,并以中等题为主”改为“试卷应由容易题、中等难度题和难题组成,总体难度要适当,并以中等难度题为主”.第一部分:2009年高考考试大纲解读③前言中,删去了下面两段话:
题型是呈现考试内容的形式.不同的题型,在考查不同知识、能力及其层次上有不同的功能.因此,《考试大纲》根据考试内容也提出了相应的题型.
在总结2007年命题经验和考情况的基础上,作了适当修订,以便更好的适应高校招生需要和中学教学实际,力求对中学全面实施素质教育发挥积极的作用.●考试性质
普通高等学校招生全国统一考试是合格的高中毕业生和具有同等学力的考生参加的选拔性考试.高等学校根据考生成绩,按已确定的招生计划,德、智、体全面衡量,择优录取.因此,高考应具有较高的信度、效度,必要的区分度和适当的难度.理 科文 科●考试要求一、命题原则
数学科的考试,按照“考查基础知识的同时,注重考查能力”的原则,确立以能力立意命题的指导思想,将知识、能力和素质融为一体,全面检测考生的数学素养.
数学科考试要发挥数学作为基础学科的作用,既考查中学数学的知识和方法,又要考查考生进入高校继续学习的潜能.(2007年北京卷理19题)如图,有一块半椭圆形钢板,其长半轴为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.
(I)求面积S以为自变量x的函数式,并写出其定义域;
(II)求面积S的最大值.二、考试要求1.知识要求
对数学基础知识的考查,要既全面又突出重点,对于支撑学科知识体系的重点内容,要占有较大的比例,构成数学试卷的主体.注重学科的内在联系和知识的综合性,不刻意追求知识的覆盖面.从学科的整体高度和思维价值的高度考虑问题,在知识网络交汇点设计试题,使对数学基础知识的考查达到必要的深度.★ 一是重点内容重点考查(1)函数、导数与不等式(2008年全国Ⅱ卷理第22题)
设函数
(Ⅰ)求f(x)的单调区间;
(Ⅱ)如果对任何x≥0,都有f(x)≤ax,求a的取值范围.(2)数列(2008年全国Ⅱ卷理第22题) 设函数 f(x) =x-xlnx.数列{an}满足0
(Ⅱ)证明:an< an+1<1;
(Ⅲ)设b∈(a1,1),整数 证明:ak+1>b.(3)三角函数 (2008年全国Ⅰ卷理科第17题)设△ABC的内角A,B,C所对的边长分别为a,b,c,
且
(Ⅰ)求tanAcotB的值;
(Ⅱ)求tan(A-B)的最大值. 解(Ⅰ) 即 展开并整理得: 所以tanAcotB=4. (Ⅱ) 由(Ⅰ)得:tanA=4tanB. 当且仅当(4)立体几何(2007年Ⅱ卷理第19题)在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点.
(1)证明EF∥平面SAD;
(2)设SD=2DC,求二面角A-EF-D的大小.(2)解法一:不妨设DC=2,
则SD=4,DG=2 .ASBCDEFGH取AG的中点H,连结DH,则DH⊥AG.又AB⊥平面SAD,所以
AB ⊥DH,从而
DH⊥平面 AEF.ASBCDEFGMH取EF的中点M,连结MH,则
MH⊥EF.连结DM,HM,则MH⊥EF.故∠DMH为二面角A-EF-D的平面角.所以二面角A-EF-D的大小为解法二:取DS的中点为G,
DC的中点为H,连结AG,
FG,FH,EH,ASBCDEFGMH则三棱柱AGD-EFH为直三棱柱。取EF的中点为M,连结DM,
HM,则∠DMH为二面角A-EF-D的余角.(2007年Ⅰ卷理第19题)四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2 ,SA=SB=
(Ⅰ)证明SA⊥BC;
(Ⅱ)求直线SD与平面SAB所成角的大小.SABCDO(5)解析几何(2008年全国Ⅰ卷理第21题)双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于两点A,B.已知|OA|,|AB|,|OB|成等差数列,且 与 同向.
(Ⅰ)求双曲线的离心率;
(Ⅱ)设AB被双曲线所截得的线段的长为4,求双曲线的方程.解法一:设出渐近线与直线AB的方程,然后求出A,B两点坐标,再利用|OA|,|AB|,|OB|成等差数列得到a与b的关系,最后求出离心率.解法二:由|OA|,|AB|,|OB|成等差数列及勾股定理得到4|OA|=3|AB|,所以然后即可得到a与b的关系,最后求出离心率.解法三、 |FA|= b,所以|OA|=a.设|OB|=n,|FB|=q,则 (6)概率与统计(2008年全国Ⅰ卷理第20题)已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性的即没患病.下面是两种化验方法:
方案甲:逐个化验,直到能确定患病动物为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
(Ⅰ)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;
(Ⅱ)?表示依方案乙所需化验次数,求? 的期望.分析: (Ⅰ)设依方案甲所需化验次数为?,则?的所有可能取值为1,2,3,4. 设依方案乙所需化验次数为?,则?的所有可能取值为2,3. 当?=2时,要分两种情况:将3只血液混在一起化验的结果呈阳性与将3只血液混在一起化验的结果呈阴性,所以甲乙则依方案甲所需化验次数不少于依方案乙所需化验次数包括“?=2,且?=2”、“? =3,且? =2或? =3” 与“? =4,且? =2或? =3”,它们是彼此互斥事件,所以依方案甲所需化验次数不少于依方案乙所需化验次数的概率为(Ⅱ)E?=2×0.6+3×0.4=2.4,即依方案乙所需化验次数?的期望为2.4.★二是加强知识的综合性 (2007年Ⅰ卷第12题)(难度系数:0.466)
函数 的一个单调增区间是★三是对基础知识的考查要达到必要的深度解法一:解法二: 解法三:由柯西不等式得:解法四: 由m?n≤|m|?|n|得: 解法五: 直线 通过点M(cos?,sin?),则整理得: a2+b2≥a2b2,所以解法六:如图,由图1可以排除A选项,由图2可以排除B、C选项,所以应该选D。xya11图1xyba图2b11(2008年全国Ⅰ卷理第14题)(难度系数0.316)已知抛物线y=ax2-1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 .(2008年全国Ⅰ卷理第16题)(难度系数0.075)等边三角形ABC与正方形ABDE有一公共边AB,二面角C-AB-D的余弦值为 ,M,N分别是AC,BC的中点,则EM,AN所成角的余弦值等于 . 对数学思想和方法的考查是对数学知识在更高层次上的抽象和概括的考查,考查时必须要与数学知识相结合,通过数学知识的考查,反映考生对数学思想和方法的理解;要从学科整体意义和思想价值立意,注意通性通法,淡化特殊技巧,有效地检测考生对中学数学知识中所蕴涵的数学思想和方法的掌握程度.(2007年Ⅰ卷理17题文第20题)设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA.
(Ⅰ)求B的大小;
(Ⅱ)求cosA+sinC的取值范围.函数的思想解:(Ⅰ)根据正弦定理得sinA=2sinBsinA,(Ⅱ)方程的思想数形结合的思想(2005年全国Ⅰ卷理科第12题)
过三棱柱任意两个顶点的直线共15条,其中异面直线有
(A)18对
(B)24对
(C)30对
(D)36对分类讨论的思想转化与化归的思想ABCDEFGMNGMNO(H)特殊与一般的思想(全国甲卷文理科第4题)设三棱柱ABC-A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,则四棱锥B-APQC的体积为
(A)
(B)
(C)
(D)xyPQFO有限与无限的思想 一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜。记三种盖法屋顶面积分别为p1、p2、p3. ① ② ③
若屋顶斜面与水平面所成的角都是?,则(2001年全国新课程理科第11题)2.能力要求
对数学能力的考查,强调 “以能力立意”,就是以数学知识为载体,从问题入手,把握学科的整体意义,用统一的数学观点组织材料,侧重体现对知识的理解和应用,尤其是综合和灵活的应用,以此来检测考生将知识迁移到不同情景中去的能力,从而检测出考生个体理性思维的广度和深度以及进一步学习的潜能. (1)思维能力
对能力的考查,以思维能力为核心,全面考查各种能力,强调综合性、应用性,并切合考生实际. (2006年北京卷理文8题)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口 A、B、 C 的机动车辆数如图所示,图中 x1, x2, x3分别表示该时段单位时间通过路段 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则 (A)x1>x2>x3 ? ? (B)x1> x3 > x2
(C)x2 > x3> x1? (D)x3 > x2> x1(2007年广东卷第7题)图3是某汽车维修公司的维修点环形分布图,公司在年初分配给A、B、C、D四个维修点某种配件各50件.在使用前发现需将A、B、C、D四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进行.那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为
A.18 B.17 C.16 D.15方案一:从A往D调动10件,从C往D调动1件,从B往C调动5件;方案二:从A往D调动11件,从B往A调动1件,从B往C调动4件; 设这四个维修点A,B,C,D处的调动件数分别为xA,xB, xCxD,则有xA≥|50-40|=10, xB≥|50-45|=5,
xC≥|50-54|=4, xD≥|50-61|=11,所以总的调动件数n不小于不相邻的维修点之间调动件数之和,即n≥14且n≥16.y=|x1|+|x2|+|x3|+|x4|=|x1|+|x1+5|+|x1+1|+|x1-10|≥|(x1-10)-(x1+5)|+|(x1+1)-x1|=11+5=16, 当(x1-10)(x1+5)≤0且x1(x1+1)≤0
时等号成立,这时0≤x1≤ -1. (2006年全国甲卷理12题)A.190 B.171
C.90 D.45方法一: 第一个等号当9≤x≤11时取到,第二个等号当x=10时取到,所以当x=10时f(x)取到最小值90.方法二:利用绝对值的性质,则有f(x)=|x-1|+|x-2|+???+|x-9|+|x-10|+|x-11|+???+|x-19|≥|x-1+x-2+???+x-9+11-x+???+19-x|+|x-10|=90+|x-10|≥90.方法三:利用绝对值的性质,则有|x-1|+|x-19|≥19-1=18,等号当1≤x≤19时取到;|x-2|+|x-18|≥18-2=16,等号当2≤x≤18时取到;|x-3|+|x-17|≥17-3=14 ,等号当3≤x≤17时取到;… …|x-9|+|x-11|≥11-9=2 ,等号当9≤x≤11时取到;|x-10|≥0 ,等号当x=10时取到;所以当x=10时f(x)取到最小值为 18+16+14+…+2=90. 对运算能力的考查主要是对算理和逻辑推理的考查,考查时以代数运算为主,同时也考查估算、简算.(2)运算能力如图,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF∥AB,EF,EF与面AC的距离为2,则该多面体的体积为(1999年全国卷理10题)ABEFCD明显VABCDEF>VE-ABCD =6,所以可以排除A、B、C,故D正确. 对空间想象能力的考查,主要体现在对文字语言、符号语言及图形语言三种语言的互相转化,表现为对图形的识别、理解和加工,考查时要与运算能力、逻辑思维能力相结合.(3)空间想象能力(2007年海宁卷理第8题)已知某个几何体的 三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是20 正视图侧视图10俯视图20 20 10(2007年海宁卷理第12题)一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为h1,h2 ,h3,则h1:h2 :h3=一、高考复习的基本经验
1.总体安排
第一轮:9月至第二年3月
——基础知识过关(逐章复习);
第二轮:3月至5月初
——综合能力突破(专题复习);
第三轮:5月初至5月底
——综合能力提升(查缺补漏).第二部分:高考备考策略二、高考复习的几个误区(1)高考试题的一个重要来源就是课本1.以复习资料为纲,偏离课本(2)基本概念的定义应以课本为准(3)基本方法的一个重要来源就是课本(4)解题格式的规范标准来源于课本(课本第三册第一章复习参考题B组第2题)在一个单位普查某种疾病,1000个人去验血,对这些人的血的化验可以用两种方法进行:
(Ⅰ)每个人的血分别化验,这时需要化验1000次;
(Ⅱ)把每个人的血样分成两份,取k个人的血样各一份混在一起进行,如果结果是阴性的,那么对这k个人只作一次检验就够了;如果结果是阳性的,那么再对这k个人的另一份血样逐个化验,这时对这k个人共需作k+1次化验.
假定对所有人来说,化验结果是阳性的概率是0.1,而且这些人的反映是独立的,试比较两种方法所需化验次数的多少.对此问题作一般化的讨论.(1)高考试题的一个重要来源就是课本(2005年湖北理第19题)某地最近出台一项机动车驾照考试规定;每位考试者一年之内最多有4次参加考试的机会,一旦某次考试通过,使可领取驾照,不再参加以后的考试,否则就一直考到第4次为止.如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9,求在一年内李明参加驾照考试次数?的分布列和?的期望,并求李明在一年内领到驾照的概率.(课本1.2离散型随机变量的期望与方差的例3)有一批数量很大的产品,其次品率为15%,对这批产品进行抽查,每次抽出1件,如果抽出次品,则终止抽查,否则继续抽查,直到抽出次品,但抽查次数最多不超过10次,求抽取次数的期望.(2)基本概念的定义应以课本为准(2004年湖北理第16题)某日中午12时整,甲船自A处以16km/h的速度向正东行驶,乙船自A的正北18km处以24km/h的速度向正南行驶,则当日12时30分时两船之间距离对时间的变化率是 km/h.(2008年北京卷理第12题) 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为 (0,4), (2,0), (6,4),则f(f(0)= ;
(用数字作答)C yx1234562134BA(2008年全国Ⅱ卷理科第16题)平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:
充要条件① ;
充要条件② .
(写出你认为正确的两个充要条件)例:写出p且q形式的复合命题
p:邻边相等的平行四边形是正方形;
q:邻边互相垂直的平行四边形是正方形;p且q的复合命题:
邻边相等且邻边互相垂直的平行四边形是正方形; 邻边相等的平行四边形是正方形且邻边互相垂直的平行四边形是正方形.例:命题p :“若(x-1)(x-2)=0,则x =1”的否定是 .【例】写出下列命题的否定:
(1)2是偶数;
(2)奇数是质数;
(3)菱形的对角线相等.错解:若(x-1)(x-2)=0,则x≠1;正解:存在x∈R,(x-1)(x-2)=0,且x≠1.(2007年山东卷文理第7题)命题“对任意的x∈R, x3-x2+1≤0”的否定是
A.不存在x∈R, x3-x2+1≤0
B.存在x∈R, x3-x2+1≤0
C.存在x∈R, x3-x2+1>0
D.对任意的x∈R, x3-x2+1>0 【例】由0到9这10个数字可以组成多少个从左到右恰好是从大到小排列的三位数?【例】5个人排成一排,要求A必须在B的右边(可以不相邻),有多少种不同的排法?(3)基本方法的一个重要来源就是课本(2007年山东卷理第17题)设数列{an}满足,
(1)求数列{an}的通项;
(2)设 求数列{bn}的前n项和Sn.(2008年全国Ⅱ卷)设数列{an}的前n项和为Sn,已知a1=a, an+1=Sn+3n (n∈N*) ,设bn=Sn-3n ,求数列{bn}的通项.解法一:由 an+1=Sn+3n 得: an=Sn-1+3n-1 ,两式相减得:两边都相减去2?3n得:所以数列{an-2?3n-1}是以a-2为首项,以2为公比的等比数列,故解法二:由 an+1=Sn+3n 得: Sn+1-Sn=Sn+3n,即两边都相减去3n+1得:所以数列{Sn-3n}是以a-3为首项,以2为公比的等比数列,故由 an+1=Sn+3n 得: an=Sn-1+3n-1 ,解法一解法二 Sn+1-Sn=Sn+3n,由 an+1=Sn+3n 得:(4)解题格式的规范标准来源于课本2.不重视对考试大纲与高考试题的研究《考试大纲》的要求:了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项.①递推数列: (2004年Ⅲ卷理科第15题)
已知数列{an}满足a1=1,an = a1+2a2+…
+(n-1) an-1(n≥2),则它的通项公式(2007年全国Ⅱ卷理第21题)设数列{an}的首项
a1∈(0,1),
(1)求{an}的通项公式;
(2)设 ,证明bn< bn+1 ,其中n为正整数.(2007年全国Ⅰ卷理22题)已知数列{an}中,a1=2,
(Ⅰ)求{an}的通项公式;
(Ⅱ)若数列{bn}中,
证明:(2008年全国Ⅱ卷)设数列{an}的前n项和为Sn, 已知a1=a, an+1=Sn+3n (n∈N*) .
(Ⅰ)设bn=Sn-3n ,求数列{bn}的通项;
(Ⅱ)若an+1 ≥an, n∈N*,求a的取值范围.②数列求和:
《考试大纲》与《教学大纲》中没有明确的考查要求,但在高考中却有一般数列的求和问题.设正项等比数列{an}的首项a1= ,前n项和为Sn,且210S30-(210+1)S20+S10=0.
(Ⅰ)求{an}的通项;
(Ⅱ)求{nSn}的前n项和Tn.(2005年全国Ⅰ卷文21题)(2007年全国乙卷文第22题)设{an}是等差数列, {bn}是各项都为正数的等比数列,且a1=b1=1, a3+b5=21, a5+b3=13 .
(Ⅰ)求{an} , {bn}的通项公式;
(Ⅱ)求数列 的前n项和Sn . ③概率与统计
考试要求
(1)了解随机变量、离散型随机变量的意义,会求出某些简单的离散型随机变量的分布列.
(2)了解离散型随机变量的期望值、方差的意义,会根据离散型随机变量的分布列求出期望值、方差.
(3)会用抽机抽样,系统抽样,分层抽样等常用的抽样方法从总体中抽取样本.
(4)会用样本频率分布去估计总体分布.
(5)了解正态分布的意义及主要性质.
(6)了解线性回归的方法和简单应用. 这一层次所涉及的主要行为动词有:了解,知道、识别、模仿,会求、会解等. 了解:要求对所列知识的含义有初步的、感性的认识,知道这一知识内容是什么,按照一定的程序和步骤照样模仿,并能(或会)在有关的问题中识别和认识它. 在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布N(70,100).已知成绩在90分以上(含90分)的学生有12名.
(Ⅰ)试问此次参赛学生总数约为多少人?
(Ⅱ)若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?
可共查阅的(部分)标准正态分布表Ф(X0)=P(x
A.0.16 B.0.32 C.0.68 D. 0.84 (2007年湖南理第5题)设随机变量ξ服从标准 正态分布N(0,1),已知Φ(-1.96)=0.025,则P(|ξ|<1.96)=( )
A.0.025 B.0.050 C.0.950 D.0.975(2008年安徽卷第10题)设两个正态分布N(?1,?1) (?1>0)和N(?2,?2) (?2>0)的密度函数图像如图所示.则有
A. ?1?2
C. ?1>?2, ?1?2, ?1>?2 (2008年湖南卷第4题)设随机变量?服从正态分布N(2,9),若P(?>c+1)=P(?
(A) (B) (C) (D)(2007年广东卷理17题)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y (吨标准煤)的几组对照数据
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y = x+a;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)1.关于专题的选择三、最后阶段的复习(1)高考的重点与热点;
(2)学习中的难点;
(3)数学思想方法;
(4)选择题填空题等的答题技巧;1.函数与导数;
2.数列;
3.三角函数;
4.立体几何;
5.解析几何;
6.概率与统计.1.数学思想方法;
2.选择题的求解策略;
3.填空题的求解策略;
4.基本解答题的求解策略;
5.综合题的求解策略; 应注意的问题
①突出主干知识和重点,抓大放小;
选择适当的专题,引导学生对知识体系进行自主构建,突出重点内容,设置适量问题,这是对专题知识部分的基本要求.忌讳专题选择过多,设置问题过多.②注重对相关问题的整合,减轻学生负担,提高课堂效益.
学生普遍反感和憎恨的事情,就是作业太多.让学生无奈的是有些习题教师也没有经过精选,甚至出现整套题下发、重复题出现,白白浪费了学生宝贵的时间. 2.关于模拟练习
(1)30分钟卷:8道选择题,2道填空题;
(2)45分钟卷:8道选择题,2道填空题,2道解答题;
(3)100分钟卷:10道选择题,3道填空题,5道解答题;
(4)120分钟卷:12道选择题,4道填空题,6道解答题;3.关于试卷讲评
(1)讲试题的背景及考查重点;
(2)讲试题的解答思路与思维历程;
(3)讲学生的作答情况,主要是存在的问题;
(4)讲试题的拓展、变式等.4.关于最后阶段的复习
自主复习、查漏补缺、回归课本、注重基础、树立信心谢 谢
2009.2.14
同课章节目录
