【寒假衔接】第一单元简易方程1-3课时导学案2023-2024学年五年级下册数学苏教版
文档属性
| 名称 | 【寒假衔接】第一单元简易方程1-3课时导学案2023-2024学年五年级下册数学苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-25 12:26:54 | ||
图片预览




文档简介
第一单元:简易方程
第1课时:等式与方程
【学习目标】
1、我会理解方程的含义。
2、我能认识等式与方程的关系。(重点)
3、我可以根据情境正确列方程。(难点)
【导学过程】
一、回顾旧知(2分钟):
5x+4x= 8y-y= 7x+7x+6x=
7a×a= 15x+6x= 5b+4b-9b=
二、自主探究活动(10分钟)
1、看图写等式:
2、我会写式子表示它们的关系:
三、认识新知:(3分钟)
认识新朋友,并把你认为最关键的两个词圈出来:
像x+50=100,x+x=100这样含有未知数的等式叫方程。
四、合作交流(10分钟)
1、观察、思考并讨论,并将等式与方程的关系填入下图:
如果用集合图来表示等式和方程的关系的为,就可以表示为:
五、扩展延伸,当堂检测。
(一)、判断:如果它是等式请画△;方程请画□。
36-7=29( ) 6+x=14( ) 60+23>70( ) 8+x( )
50÷2=25( ) x+4<14( ) 5Y=40( ) y-28=35( )
(二)、判断:
1、含有未知数的式子叫做方程。 ( )
2、方程一定是等式。 ( )
3、1.5+X是方程。 ( )
4、等式一定是方程。 ( )
(三)、
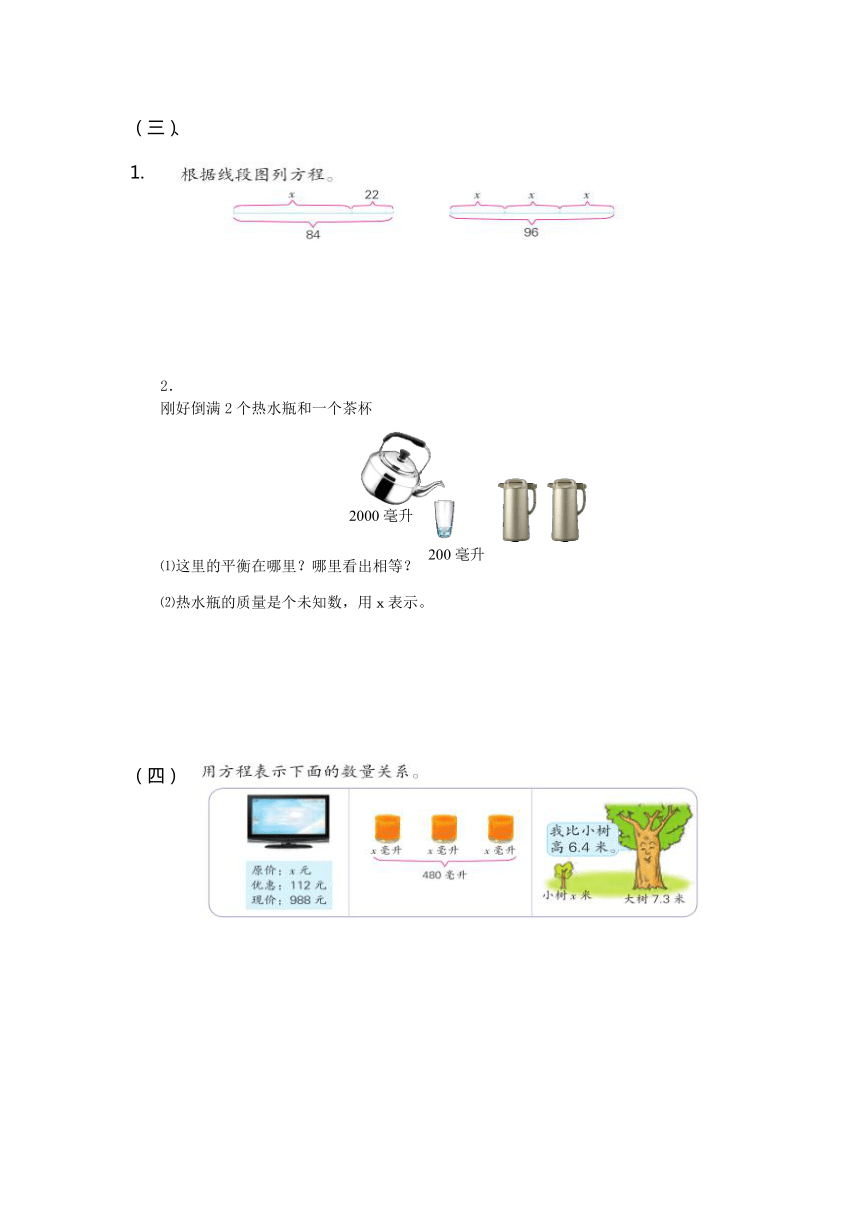
1.
2.
刚好倒满2个热水瓶和一个茶杯
⑴这里的平衡在哪里?哪里看出相等?
⑵热水瓶的质量是个未知数,用x表示。
(四)
第2课时 等式的性质与解方程(1)
【学习目标】
初步理解“方程的解”、“解方程”的含义
2、初步理解等式的基本性质,能用等式的性质解简易方程。(重点)
3、理解由具体的实例抽象出等式的性质的过程(难点)
【导学过程】
一、回顾旧知
判断:如果它是等式请画△;方程请画□
6+x=14 36-7=29 60+23≠70 8+x
50÷2=25 x+4<14 y-28=35 5y=40
二、自主探究活动
1、看图填空。
20 ○20 20+( )○20+( )
○50 +( )○50+( )
50+a○ 50+a 50+a-( )○ 50+a-( )
2、讨论:第一竖排和第二竖排的式子相比,发生了怎样的变化?他们有什么共同的地方?
3、等式的性质:
等式的两边同时加上或减去同一个数,所得结果仍然是等式。
4、试一试:根据等式的性质在○里填运算符号,在□里填数。
○□ ○□
三、认识新知:
使方程两边相等的未知数的值叫作 ,
求方程的解的过程,叫作 。
试一试:利用等式的性质解下列方程.
X+75=105 x-23=52
四、扩展延伸,当堂检测:
1、在括号里找出方程的解,并在下面划横线。
x+22=78 (x=100,x=56)
x-2.5=2.5 (x=0, x=5)
2、解方程。
76+x=105 x-6.4=0.4
3、看图列方程并解答。
第3课时 等式的性质与解方程(2)
【学习目标】
1、理解并掌握等式的性质,即在等式两边都乘或除以同一个数(除以一个数时0除外),所得结果仍然是等式的性质。 (重点)
2、能掌握利用相应的性质解一步计算的方程。
【导学过程】
一、回顾旧知(2分钟):
说一说等式的性质是什么,用等式的性质如何下列解方程.
9+x=24 y-17=43
15+x=24 y-27=31
二、自主探究活动(10分钟)
1、看图填空。
○20 2○20×( )
3x○60 3x÷3○ 60÷( )
2、小组讨论:第二个等式与第一个等式相比,发生了怎样的变化?他们有什么共同的地方?
3、等式两边可以同时除以0吗?为什么?
4、等式的性质2:
等式两边同时乘或除以同一个不等于0的数,所得结果仍然是等式。
5、试一试:根据等式的性质在○里填运算符号,在□里填数。
○□ ○□
三、巩固提高(8分钟)
花园小学有一块长方形试验田(如右图),求试验田的宽。(先说数量关系,再试着列方程解方程)
四、扩展延伸,当堂检测:(15分钟)
1、解方程。
①12x=96 ②x÷40=14 ③x÷2.5=5
2、
列方程求表中未知数的值。
物品名称 单价 数量 总价
墨水 元/瓶 12瓶 31.2元
钢笔 9.6元/支 y支 48元
第1课时:等式与方程
【学习目标】
1、我会理解方程的含义。
2、我能认识等式与方程的关系。(重点)
3、我可以根据情境正确列方程。(难点)
【导学过程】
一、回顾旧知(2分钟):
5x+4x= 8y-y= 7x+7x+6x=
7a×a= 15x+6x= 5b+4b-9b=
二、自主探究活动(10分钟)
1、看图写等式:
2、我会写式子表示它们的关系:
三、认识新知:(3分钟)
认识新朋友,并把你认为最关键的两个词圈出来:
像x+50=100,x+x=100这样含有未知数的等式叫方程。
四、合作交流(10分钟)
1、观察、思考并讨论,并将等式与方程的关系填入下图:
如果用集合图来表示等式和方程的关系的为,就可以表示为:
五、扩展延伸,当堂检测。
(一)、判断:如果它是等式请画△;方程请画□。
36-7=29( ) 6+x=14( ) 60+23>70( ) 8+x( )
50÷2=25( ) x+4<14( ) 5Y=40( ) y-28=35( )
(二)、判断:
1、含有未知数的式子叫做方程。 ( )
2、方程一定是等式。 ( )
3、1.5+X是方程。 ( )
4、等式一定是方程。 ( )
(三)、
1.
2.
刚好倒满2个热水瓶和一个茶杯
⑴这里的平衡在哪里?哪里看出相等?
⑵热水瓶的质量是个未知数,用x表示。
(四)
第2课时 等式的性质与解方程(1)
【学习目标】
初步理解“方程的解”、“解方程”的含义
2、初步理解等式的基本性质,能用等式的性质解简易方程。(重点)
3、理解由具体的实例抽象出等式的性质的过程(难点)
【导学过程】
一、回顾旧知
判断:如果它是等式请画△;方程请画□
6+x=14 36-7=29 60+23≠70 8+x
50÷2=25 x+4<14 y-28=35 5y=40
二、自主探究活动
1、看图填空。
20 ○20 20+( )○20+( )
○50 +( )○50+( )
50+a○ 50+a 50+a-( )○ 50+a-( )
2、讨论:第一竖排和第二竖排的式子相比,发生了怎样的变化?他们有什么共同的地方?
3、等式的性质:
等式的两边同时加上或减去同一个数,所得结果仍然是等式。
4、试一试:根据等式的性质在○里填运算符号,在□里填数。
○□ ○□
三、认识新知:
使方程两边相等的未知数的值叫作 ,
求方程的解的过程,叫作 。
试一试:利用等式的性质解下列方程.
X+75=105 x-23=52
四、扩展延伸,当堂检测:
1、在括号里找出方程的解,并在下面划横线。
x+22=78 (x=100,x=56)
x-2.5=2.5 (x=0, x=5)
2、解方程。
76+x=105 x-6.4=0.4
3、看图列方程并解答。
第3课时 等式的性质与解方程(2)
【学习目标】
1、理解并掌握等式的性质,即在等式两边都乘或除以同一个数(除以一个数时0除外),所得结果仍然是等式的性质。 (重点)
2、能掌握利用相应的性质解一步计算的方程。
【导学过程】
一、回顾旧知(2分钟):
说一说等式的性质是什么,用等式的性质如何下列解方程.
9+x=24 y-17=43
15+x=24 y-27=31
二、自主探究活动(10分钟)
1、看图填空。
○20 2○20×( )
3x○60 3x÷3○ 60÷( )
2、小组讨论:第二个等式与第一个等式相比,发生了怎样的变化?他们有什么共同的地方?
3、等式两边可以同时除以0吗?为什么?
4、等式的性质2:
等式两边同时乘或除以同一个不等于0的数,所得结果仍然是等式。
5、试一试:根据等式的性质在○里填运算符号,在□里填数。
○□ ○□
三、巩固提高(8分钟)
花园小学有一块长方形试验田(如右图),求试验田的宽。(先说数量关系,再试着列方程解方程)
四、扩展延伸,当堂检测:(15分钟)
1、解方程。
①12x=96 ②x÷40=14 ③x÷2.5=5
2、
列方程求表中未知数的值。
物品名称 单价 数量 总价
墨水 元/瓶 12瓶 31.2元
钢笔 9.6元/支 y支 48元
