物理教科版必修1【2015秋备课参考课件】:1.6匀变速直线运动位移与时间的关系(3份打包)
文档属性
| 名称 | 物理教科版必修1【2015秋备课参考课件】:1.6匀变速直线运动位移与时间的关系(3份打包) |

|
|
| 格式 | zip | ||
| 文件大小 | 439.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2015-07-14 00:00:00 | ||
图片预览



文档简介
课件25张PPT。第一章 运动的描述第 6节 匀变速直线运动
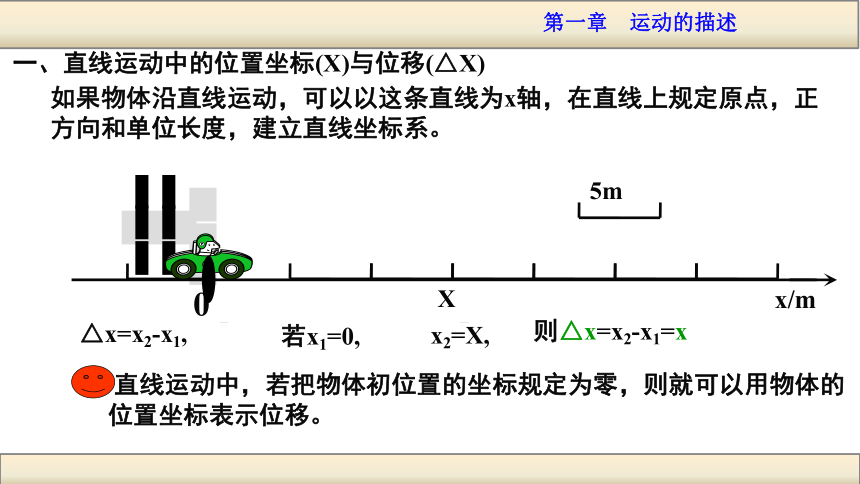
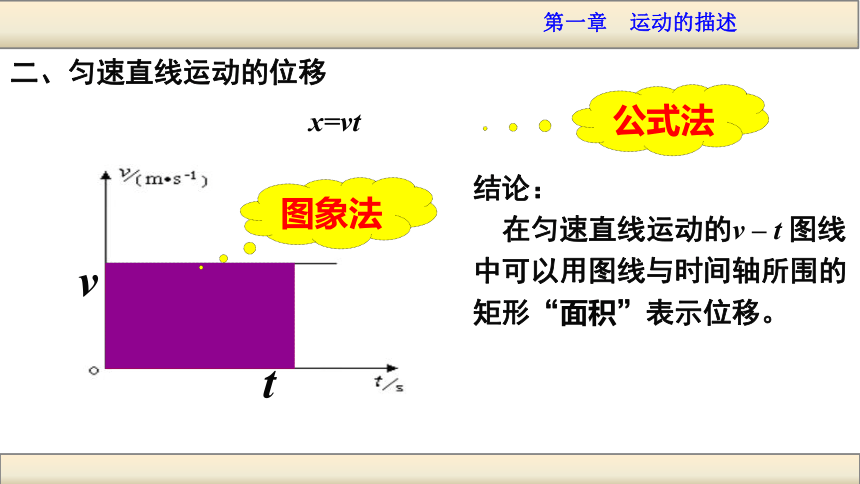
位移与时间的关系如果物体沿直线运动,可以以这条直线为x轴,在直线上规定原点,正方向和单位长度,建立直线坐标系。x/m△x=x2-x1, 若x1=0,则△x=x2-x1=x一、直线运动中的位置坐标(X)与位移(△X)X1X2Xx2=X, 直线运动中,若把物体初位置的坐标规定为零,则就可以用物体的位置坐标表示位移。二、匀速直线运动的位移x=vt v t 结论:
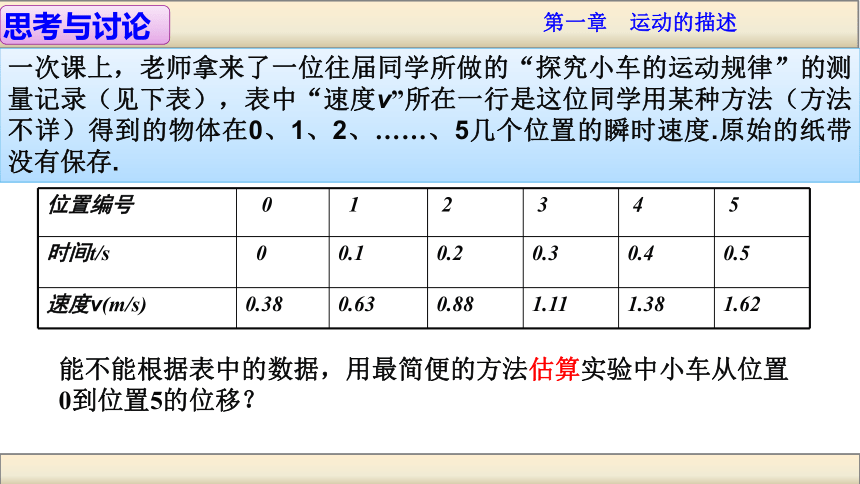
在匀速直线运动的v – t 图线中可以用图线与时间轴所围的矩形“面积”表示位移。公式法图象法v/m·s-1t/s2641083456021-2-4x面积也有正负,面积为正,表示位移的方向为正方向,面积为负值,表示位移的方向为负方向.乙X甲X乙 在匀变速直线运动中,物体的位移随时间发生变化,位移在v-t图象上表示时,是否也有类似的关系?微土不辞,终成泰山; 点滴不遗,始为沧海。一次课上,老师拿来了一位往届同学所做的“探究小车的运动规律”的测量记录(见下表),表中“速度v”所在一行是这位同学用某种方法(方法不详)得到的物体在0、1、2、……、5几个位置的瞬时速度.原始的纸带没有保存.能不能根据表中的数据,用最简便的方法估算实验中小车从位置0到位置5的位移?以下是关于这个问题的讨论。
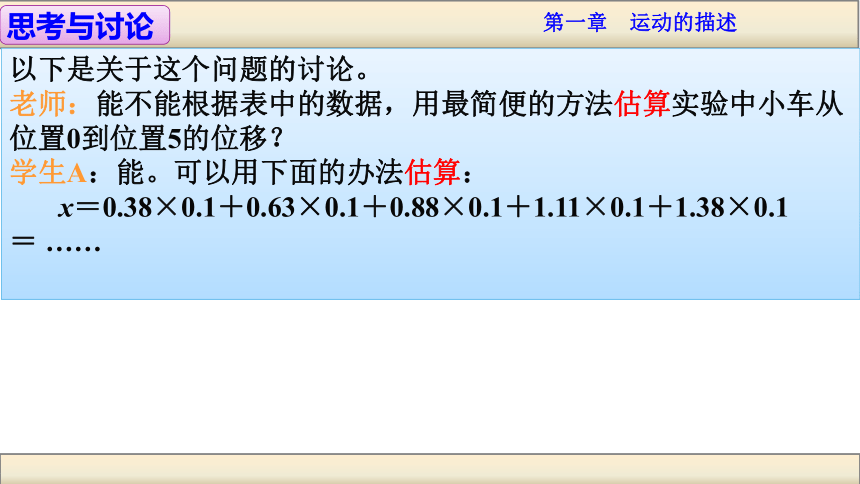
老师:能不能根据表中的数据,用最简便的方法估算实验中小车从位置0到位置5的位移?
学生A:能。可以用下面的办法估算:
x=0.38×0.1+0.63×0.1+0.88×0.1+1.11×0.1+1.38×0.1= ……
思考与讨论思考与讨论学生B:这个办法不好。从表中看出,小车的速度在不断增加,0.38只是0时刻的瞬时速度,以后的速度比这个数值大。用这个数值乘以0.1 s,得到的位移比实际位移要小。后面的几项也有同样的问题。
学生A:老师要求的是“估算”,这样做是可以的。
老师:你们两个人说得都有道理。这样做的确会带来一定误差,但在时间间隔比较小、精确程度要求比较低的时候,可以这样估算。要提高估算的精确程度,可以有多种方法。其中一个方法请大家考虑:如果当初实验时时间间隔不是取0.1 s,而是取得更小些,比如0.06 s,同样用这个方法计算,误差是不是会小一些?如果取0.04 s、0.02 s …… 误差会怎样?
欢迎大家发表意见。科学思想方法:先把过程无限分割,以“不变”近似代替“变”,然后再进行累加的思想 。这个材料中体现了什么科学思想?此科学思想方法能否应用到匀变速直线运动的v-t图象上?t/s哈哈速度-时间(v-t)图象中图线与时间轴围成的面积就代表做直线运动物体在相应时间间隔内的位移。
由图可知:梯形OABC的面积代入各物理量得:又v=v0+at三、匀变速直线运动的位移公式推导四.匀变速直线运动的位移1.位移公式:2.对位移公式的理解:⑴反映了位移随时间的变化规律。⑵因为υ0、α、x均为矢量,使用公式时应先规定正方向。(一般以υ0的方向为正方向)(3)若v0=0,(4)特别提醒:t是指物体运动的实际时间,要将位移与发生这段位移的时间对应起来.(5)代入数据时,各物理量的单位要统一.
(用国际单位)四.匀变速直线运动的位移 1.一物体做匀加速直线运动,初速度为v0=5 m/s,加速度为a=0.5 m/s2,求:(1)物体在3 s内的位移 (2)物体在第3 s内的位移.
【思路点拨】 画出运动草图:
由图可知,第3秒内的位移等于前3秒内的位移减去前2秒内的位移.1.一辆汽车以2 m/s2的加速度做匀减速直线运动,经过6秒停下来.求汽车开始减速4秒内前进的距离.
解析:选初速度v0方向为正,则a=-2 m/s2,6秒末速度v=0,由v=v0+at得:v0=v-at=0-(-2)×6 m/s=12 m/s由 得车的位移2.在平直公路上,一汽车的速度为15 m/s.从某时刻开始刹车,在阻力作用下,汽车以2 m/s2的加速度运动,问刹车后10 s末车离开始刹车点多远?错刹车问题!解:以汽车初速方向为正方向2.在平直公路上,一汽车的速度为15 m/s.从某时刻开始刹车,在阻力作用下,汽车以2 m/s2的加速度运动,问刹车后10 s末车离开始刹车点多远?由得运动时间 说明刹车后7.5 s 汽车停止运动正确解析:设车实际运动时间为t0,以汽车初速度方向为正方向位移对 位移与时间的关系也可以用图象来表示,这种图象叫位移—时间图象,即x-t图象。你能画出匀变速直线运动
的x-t图象吗?试试看。因为位移公式是关于t的一元二次函数,故x—t图象是一条抛物线(一部分)。不是物体运动的轨迹.如果一位同学问:“我们研究的是直线运动,为什么画出来的x-t图象不是直线?”你应该怎样向他解释?
位移与时间的关系如果物体沿直线运动,可以以这条直线为x轴,在直线上规定原点,正方向和单位长度,建立直线坐标系。x/m△x=x2-x1, 若x1=0,则△x=x2-x1=x一、直线运动中的位置坐标(X)与位移(△X)X1X2Xx2=X, 直线运动中,若把物体初位置的坐标规定为零,则就可以用物体的位置坐标表示位移。二、匀速直线运动的位移x=vt v t 结论:
在匀速直线运动的v – t 图线中可以用图线与时间轴所围的矩形“面积”表示位移。公式法图象法v/m·s-1t/s2641083456021-2-4x面积也有正负,面积为正,表示位移的方向为正方向,面积为负值,表示位移的方向为负方向.乙X甲X乙 在匀变速直线运动中,物体的位移随时间发生变化,位移在v-t图象上表示时,是否也有类似的关系?微土不辞,终成泰山; 点滴不遗,始为沧海。一次课上,老师拿来了一位往届同学所做的“探究小车的运动规律”的测量记录(见下表),表中“速度v”所在一行是这位同学用某种方法(方法不详)得到的物体在0、1、2、……、5几个位置的瞬时速度.原始的纸带没有保存.能不能根据表中的数据,用最简便的方法估算实验中小车从位置0到位置5的位移?以下是关于这个问题的讨论。
老师:能不能根据表中的数据,用最简便的方法估算实验中小车从位置0到位置5的位移?
学生A:能。可以用下面的办法估算:
x=0.38×0.1+0.63×0.1+0.88×0.1+1.11×0.1+1.38×0.1= ……
思考与讨论思考与讨论学生B:这个办法不好。从表中看出,小车的速度在不断增加,0.38只是0时刻的瞬时速度,以后的速度比这个数值大。用这个数值乘以0.1 s,得到的位移比实际位移要小。后面的几项也有同样的问题。
学生A:老师要求的是“估算”,这样做是可以的。
老师:你们两个人说得都有道理。这样做的确会带来一定误差,但在时间间隔比较小、精确程度要求比较低的时候,可以这样估算。要提高估算的精确程度,可以有多种方法。其中一个方法请大家考虑:如果当初实验时时间间隔不是取0.1 s,而是取得更小些,比如0.06 s,同样用这个方法计算,误差是不是会小一些?如果取0.04 s、0.02 s …… 误差会怎样?
欢迎大家发表意见。科学思想方法:先把过程无限分割,以“不变”近似代替“变”,然后再进行累加的思想 。这个材料中体现了什么科学思想?此科学思想方法能否应用到匀变速直线运动的v-t图象上?t/s哈哈速度-时间(v-t)图象中图线与时间轴围成的面积就代表做直线运动物体在相应时间间隔内的位移。
由图可知:梯形OABC的面积代入各物理量得:又v=v0+at三、匀变速直线运动的位移公式推导四.匀变速直线运动的位移1.位移公式:2.对位移公式的理解:⑴反映了位移随时间的变化规律。⑵因为υ0、α、x均为矢量,使用公式时应先规定正方向。(一般以υ0的方向为正方向)(3)若v0=0,(4)特别提醒:t是指物体运动的实际时间,要将位移与发生这段位移的时间对应起来.(5)代入数据时,各物理量的单位要统一.
(用国际单位)四.匀变速直线运动的位移 1.一物体做匀加速直线运动,初速度为v0=5 m/s,加速度为a=0.5 m/s2,求:(1)物体在3 s内的位移 (2)物体在第3 s内的位移.
【思路点拨】 画出运动草图:
由图可知,第3秒内的位移等于前3秒内的位移减去前2秒内的位移.1.一辆汽车以2 m/s2的加速度做匀减速直线运动,经过6秒停下来.求汽车开始减速4秒内前进的距离.
解析:选初速度v0方向为正,则a=-2 m/s2,6秒末速度v=0,由v=v0+at得:v0=v-at=0-(-2)×6 m/s=12 m/s由 得车的位移2.在平直公路上,一汽车的速度为15 m/s.从某时刻开始刹车,在阻力作用下,汽车以2 m/s2的加速度运动,问刹车后10 s末车离开始刹车点多远?错刹车问题!解:以汽车初速方向为正方向2.在平直公路上,一汽车的速度为15 m/s.从某时刻开始刹车,在阻力作用下,汽车以2 m/s2的加速度运动,问刹车后10 s末车离开始刹车点多远?由得运动时间 说明刹车后7.5 s 汽车停止运动正确解析:设车实际运动时间为t0,以汽车初速度方向为正方向位移对 位移与时间的关系也可以用图象来表示,这种图象叫位移—时间图象,即x-t图象。你能画出匀变速直线运动
的x-t图象吗?试试看。因为位移公式是关于t的一元二次函数,故x—t图象是一条抛物线(一部分)。不是物体运动的轨迹.如果一位同学问:“我们研究的是直线运动,为什么画出来的x-t图象不是直线?”你应该怎样向他解释?
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
