直线与圆的位置关系复习
图片预览



文档简介
(共13张PPT)
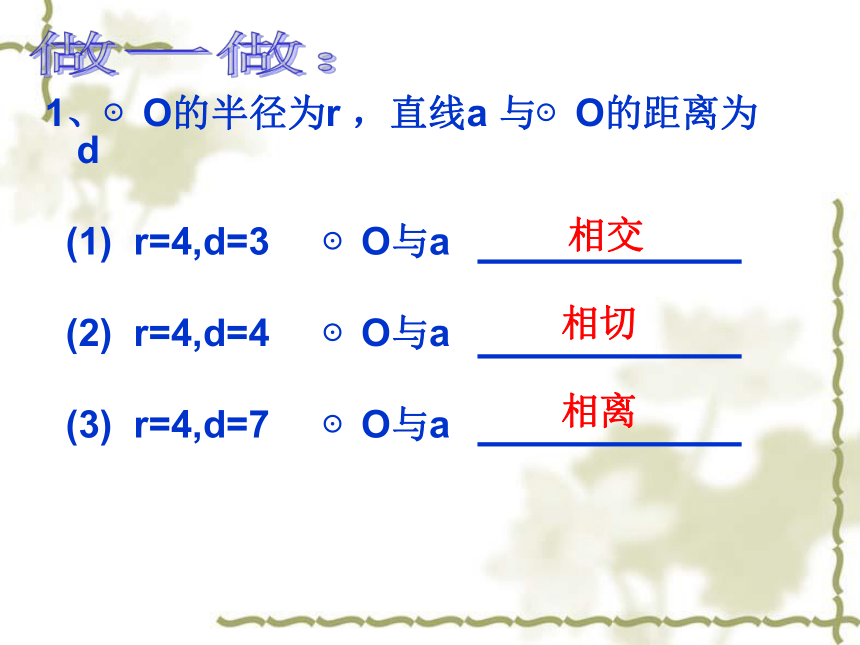
1、⊙O的半径为r ,直线a 与⊙O的距离为d
(1) r=4,d=3 ⊙O与a
(2) r=4,d=4 ⊙O与a
(3) r=4,d=7 ⊙O与a
相离
相交
相切
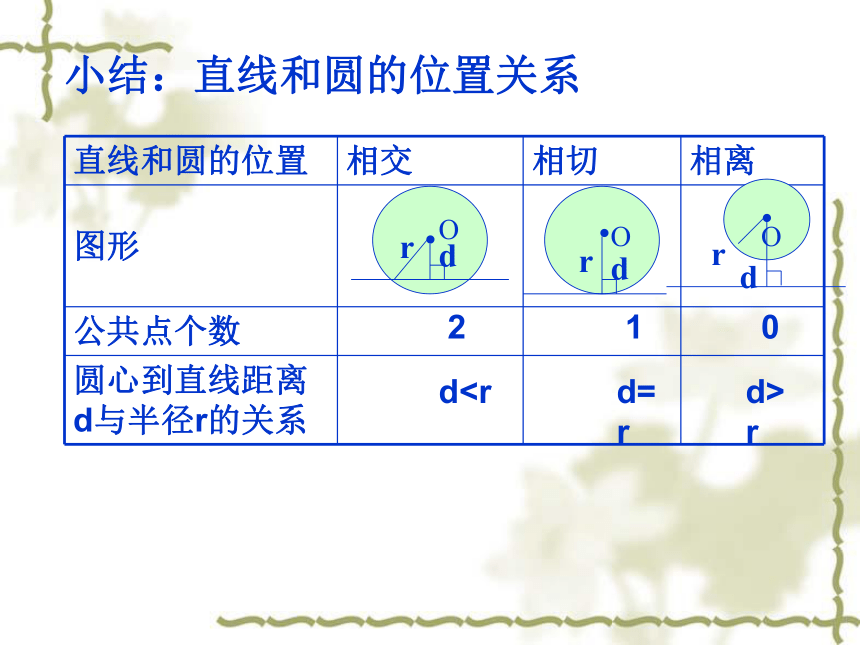
小结:直线和圆的位置关系
直线和圆的位置 相交 相切 相离
图形
公共点个数
圆心到直线距离 d与半径r的关系
2
1
0
dd=r
d>r
O
d
r
O
l
d
r
O
d
r
练习:
1、 ⊙O的直径是3,直线与⊙0相交,圆心O到直线的距离是d,则d应满足 ( )
A. d>3 B. 1.52、已知⊙O的半径是r,点O到直线l的距离为d,若d,r满足 ︱8-2r︱=0,则直线与⊙O的交点个数是 ______
c
1个
试一试:
如图,AB是⊙O的直径,下列条件,哪一条能够判定AT是⊙O的切线
(1)AB=3,AT=4,BT=5
(2)∠B=38度, ∠TAC= 38度
B
A
C
T
O
(3)∠B= ∠T
切线的判定: 经过半径的外端并且垂直于这条半径的直线是圆的切线
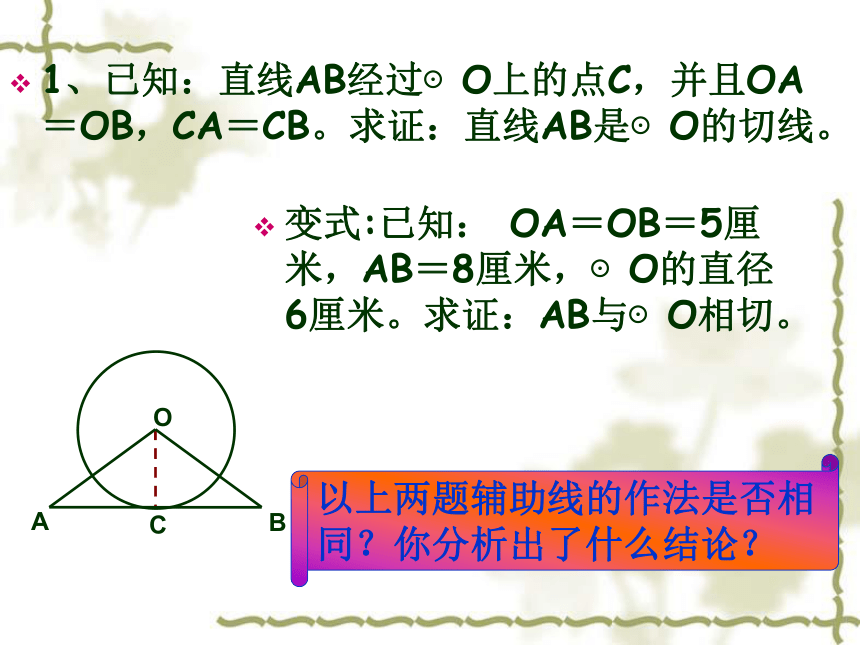
1、已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。求证:直线AB是⊙O的切线。
O
C
B
A
变式:已知: OA=OB=5厘米,AB=8厘米,⊙O的直径6厘米。求证:AB与⊙O相切。
以上两题辅助线的作法是否相同?你分析出了什么结论?
证明一条直线是圆的切线,常常需要作辅助线。
若直线过圆上某一点,则连结圆心和公共点,再证明直线与半径垂直
若直线与圆的公共点没有确定,则过圆心向直线作垂线,再证明圆心到直线的距离等于半径。
练习.如图,△ABC中,∠BCA=90°,
∠A=30°,以AB为直径画⊙O,延长AB到D,
使BD等于⊙O的半径.
求证:CD是⊙O的切线.
1如图, ⊙O切PB于点B,PB=4,PA=2,则
⊙O的半径多少?
2 如图:PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,则∠ABC=___
r=3
65度
1、经过切点的半径垂直于圆的切线。
3、经过圆心垂直于切线的直线必过切点。
2、经过切点垂直于切线的直线必过圆心。
切线的判定和性质可归纳为:已知满足
1、过圆心,2、过切点,3、垂直于切线,中任意两个,便得到第三个结论。
如图:已知PA,PB分别切⊙O于A,B两点,如果∠P=60° ,PA=2,那么AB的长为_____.
2
变式1:CD也与⊙O相切,切点为E.交PA于C点,交PB于D点,则△ PCD的周长为____.
4
E
C
D
变式2:改变切点E的位置(在略户AB上),则△ PCD的周长为____.
变式3:若PA=5则△ PCD的周长为____.
4
10
变式4:若PA=a,则△ PCD的周长为____.
2a
如图,已知C是以AB为直经的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连结AE并延长交BD于点F,直线CF交直线AB于点G.(1)求证:点F是BD的中点
(2)求证:CG是圆O的切线
巩固提高
课堂小结:
1.直线与圆的三种位置关系:相交、相切、相离
2.直线与圆相切的判定与性质
1、⊙O的半径为r ,直线a 与⊙O的距离为d
(1) r=4,d=3 ⊙O与a
(2) r=4,d=4 ⊙O与a
(3) r=4,d=7 ⊙O与a
相离
相交
相切
小结:直线和圆的位置关系
直线和圆的位置 相交 相切 相离
图形
公共点个数
圆心到直线距离 d与半径r的关系
2
1
0
d
d>r
O
d
r
O
l
d
r
O
d
r
练习:
1、 ⊙O的直径是3,直线与⊙0相交,圆心O到直线的距离是d,则d应满足 ( )
A. d>3 B. 1.5
c
1个
试一试:
如图,AB是⊙O的直径,下列条件,哪一条能够判定AT是⊙O的切线
(1)AB=3,AT=4,BT=5
(2)∠B=38度, ∠TAC= 38度
B
A
C
T
O
(3)∠B= ∠T
切线的判定: 经过半径的外端并且垂直于这条半径的直线是圆的切线
1、已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。求证:直线AB是⊙O的切线。
O
C
B
A
变式:已知: OA=OB=5厘米,AB=8厘米,⊙O的直径6厘米。求证:AB与⊙O相切。
以上两题辅助线的作法是否相同?你分析出了什么结论?
证明一条直线是圆的切线,常常需要作辅助线。
若直线过圆上某一点,则连结圆心和公共点,再证明直线与半径垂直
若直线与圆的公共点没有确定,则过圆心向直线作垂线,再证明圆心到直线的距离等于半径。
练习.如图,△ABC中,∠BCA=90°,
∠A=30°,以AB为直径画⊙O,延长AB到D,
使BD等于⊙O的半径.
求证:CD是⊙O的切线.
1如图, ⊙O切PB于点B,PB=4,PA=2,则
⊙O的半径多少?
2 如图:PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,则∠ABC=___
r=3
65度
1、经过切点的半径垂直于圆的切线。
3、经过圆心垂直于切线的直线必过切点。
2、经过切点垂直于切线的直线必过圆心。
切线的判定和性质可归纳为:已知满足
1、过圆心,2、过切点,3、垂直于切线,中任意两个,便得到第三个结论。
如图:已知PA,PB分别切⊙O于A,B两点,如果∠P=60° ,PA=2,那么AB的长为_____.
2
变式1:CD也与⊙O相切,切点为E.交PA于C点,交PB于D点,则△ PCD的周长为____.
4
E
C
D
变式2:改变切点E的位置(在略户AB上),则△ PCD的周长为____.
变式3:若PA=5则△ PCD的周长为____.
4
10
变式4:若PA=a,则△ PCD的周长为____.
2a
如图,已知C是以AB为直经的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连结AE并延长交BD于点F,直线CF交直线AB于点G.(1)求证:点F是BD的中点
(2)求证:CG是圆O的切线
巩固提高
课堂小结:
1.直线与圆的三种位置关系:相交、相切、相离
2.直线与圆相切的判定与性质
