从安徽高考三年探2009年新高考走向
图片预览







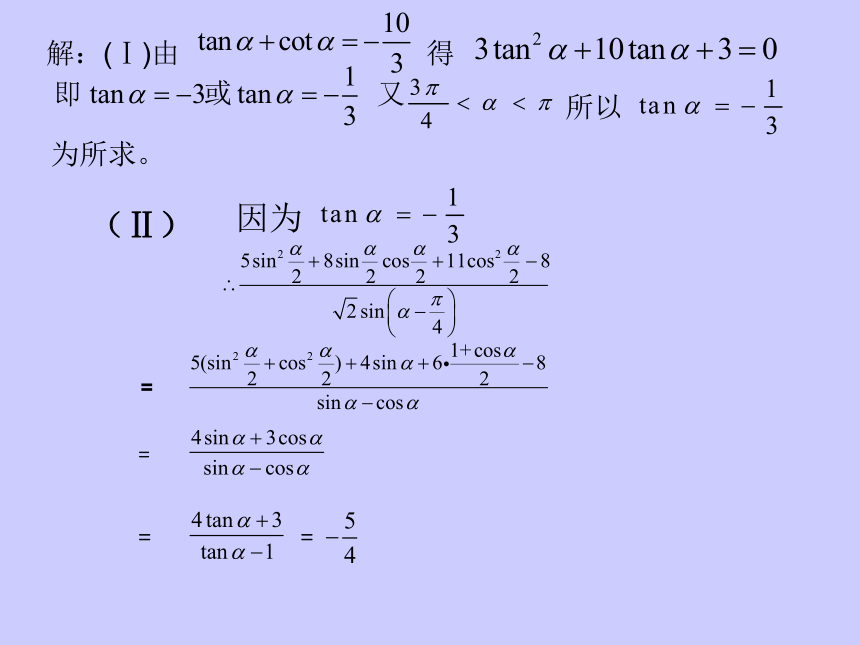




文档简介
课件113张PPT。从安徽高考三年探2009年新高考走向安庆一中程乐根报告主要内容回顾与展望
一、教育部国家命题考试中心的命题规则
二、首次安徽省高考命题形成了什么样的安徽特色?
三、安徽三年高考命题的比较与探究
四、对新增内容的探究
复习与对策
一、夯实基础有备无患
二、在复习迎考中,真正做到有意识有目标的培养学生的能力
回顾与展望一、教育部国家命题考试中心的命题规则
?考试难度系数在0.5~0.6之间
?易、中、难题的比例为3:5:2(选择题中容易题4个左右,中等难度题6个左右,难题2个左右,而难题的难度系数也只是在0.3~0.45之间)
?知识覆盖面在70%~80%之间
?试题力求保证有信度、效度、区分度、梯度二、首次安徽省高考命题形成了什么样的安徽特色?
?依然保持着国家命题中心的试卷模式
?文理科数学区别拉大,特别改变了文科数学平均分低的现状
?考查相关知识点单纯明确,不作细节纠缠
?力求体现公平性
a 背景公平
b 考生在考试方法选择上公平(如立体几何、数列解答题)三、安徽三年高考命题的比较与探究
1、客观题比较
a 题量基本上保持不变(只有07年少考了一道选择题)
b 考试内容基本保持稳定,大致上在集合、不等式、二次曲线、直线和圆、逻辑命题、三角函数的图像及性质、多面体与球、线性规划、二项式定理、数列与极限、抽象函数及基本函数的性质、导数的应用、反函数、平面向量、理科还有复数、统计(07、08两年都出了正态分布题)。估计2009年要在新增内容上出题,如:立体几何中的 三视图、幂函数、积分、框图、算法、坐标系与参数方程等等我想不超过四题。c 试题难度大多较平和,无偏题、怪题。
d 解题方法以直接法为主,同时兼顾间接法;
直接法和间接法所用时间差异不明显,意在注重基础,增加考题效度。
间接法主要是特殊值法、淘汰法、数形结合法,代人验证法。并无只有间接法能解而直接法不能解的题,也没有用间接法解很简单而直接发很繁的题目。2、解答题比较
三角解答题:
2006年(理):
17、已知
(Ⅰ)求 的值;
(Ⅱ)求的值。解:(Ⅰ)由 得
即 又 所以为所求。(Ⅱ)====因为2007年(理):
16 已知 为 的最
小正周期, ,且
求 的值. 本题主要考查周期函数、平面向量数量积与三角函数基本关系式,考查运算能力和推理能力.
解:因为 为 的最小正周期,故 .
因 ,又 .
故 .
由于 ,所以
.2008年(理):
17已知函数 .
(I)求函数 的最小正周期和图象的对称轴方程.
(II)求函数 在区间上的 值域.解:(Ⅰ)
周期 .
由 ,得 ( )
函数图象的对称轴方程为 ( ).2006年(文):
17、已知
(Ⅰ)求 的值;
(Ⅱ)求 的值。 解:(Ⅰ)由 ,得 ,所以
=
(Ⅱ)∵ ,
∴2007年(文):
16、解不等式
解:因为对任意 ,所以原不等式等价于.
即故解为.
所以原不等式的解集为2008年(文):
同2008年(理)一样 三角题的特点:
1、依然是在求值和函数性质上出题,实质依然是化简。
2、三年题所考的方法都是通法通则。
3、难度都不大,无论是对理科考生还是文科考生都起到了定心丸的作用。
对09年的展望:
依然会维持稳定的现状。要注意平面几何三角形背景下的运算问题以及解三角形问题。统计与概率题:2006年(理)
18、在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。用 表示所选用的两种不同的添加剂的芳香度之和。(以列表的形式给出结论,不必写计算过程)
的数学期望(Ⅰ)写出的分布列;
(Ⅱ)求
(要求写出计算过程或说明道理) 解(Ⅰ)
(Ⅱ)2007年(理)
20.在医学生物学试验中,经常以果蝇作为试验对象.一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子,6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.以 表示笼内还剩下的果蝇的只数.
(Ⅰ)写出的分布列(不要求写出计算过程);
(Ⅱ)求数学期望 ;
(Ⅲ)求 概率.20.本小题主要考查等可能场合下的事件概率的计算、离散型随机变量的分布列、数学期望的概念及其计算,考查分析问题及解决实际问题的能力
解:(Ⅰ)的分布列为:
(Ⅱ)数学期望为
(Ⅲ)所求的概率为.2008年(理)
19(本小题满分12分)
为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物.某人一次种植了n株沙柳.各株沙柳的成活与否是相互独立的,成活率为p,设 为成活沙柳的株数,数学期望 为3,标准差 为 .
(Ⅰ)求 的值,并写出 的分布列;
(Ⅱ)若有3株或3株以上的沙柳未成活,则需要补种,求需要补种沙柳的概率.解:由题意知,服从二 项分布 ,
.
(Ⅰ)由 ,得 从而
的分布列为
(Ⅱ)记“需要补种沙柳”为事件A,则 ,
得 ,
或 .2006年(文)
18、在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。
(Ⅰ)求所选用的两种不同的添加剂的芳香度之和等于4的概率;
(Ⅱ)求所选用的两种不同的添加剂的芳香度之和不小于3的概率;
解:设“所选用的两种不同的添加剂的芳香度之和等于4”的事件为A,“所选用的两种不同的添加剂的芳香度之和不小于3”的事件为B
(Ⅰ)芳香度之和等于4的取法有2
种: 、 ,
故
(Ⅱ)芳香度之和等于1的取法有1种: ;芳香度之和等于2的取法有1种: ,故
2007年(文)
19.(本小题满分13分)
在医学生物试验中,经常以果蝇作为试验对象.一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.
(I)求笼内恰好剩下1只果蝇的概率;
(II)求笼内至少剩下5只果蝇的概率.解:以 表示恰剩下 只果蝇的事件 .
以 表示至少剩下 只果蝇的事件 .
当事件 发生时,第 只飞出的蝇子是苍蝇,
且在前 只飞出的蝇子中有1只是苍蝇,所以2008年(文)
18、(本小题满分12分)
在某次普通话测试中,为测试汉字发音水平,设置了10张卡片,每张卡片印有一个汉字的拼音,其中恰有3张卡片上的拼音带有后鼻音“g”.
(Ⅰ)现对三位被测试者先后进行测试,第一位被测试者从这10张卡片总随机抽取1张,测试后放回,余下2位的测试,也按同样的方法进行。求这三位被测试者抽取的卡片上,拼音都带有后鼻音“g”的概率。
(Ⅱ)若某位被测试者从10张卡片中一次随机抽取3张,求这三张卡片上,拼音带有后鼻音“g”的卡片不少于2张的概率。 18解:
(1)每次测试中,被测试者从10张卡片中随机
抽取1张卡片上,拼音带有后鼻音“g”的概率为 ,
因为三位被测试者分别随机抽取一张卡片的事件是相互独
立的,因而所求的概率为
(2)设 表示所抽取的三张卡片中,恰有张卡片带有后鼻音“g”的事件,且其相应的概率为 则
因而所求概率为
概率统计题的特点:
1、理科三年均在等可能性场合下的概率计算、离散型随机变量分不列、期望上出题(2008年多考了一个标准差);文科则基本上在等可能事件、互斥事件上出题。
2、三年的运算量都不大,只涉及简单的排列组合运算,理科甚至可不用排列组合运算。
3、07年的题几乎延续了06年的出题风格,08年则改变了出题风格。三年是一个稳中渐变的过程。
4、难点依然放在如何面对实际问题,能准确识别数学模型上,突出了识别数学模式能里的考察。
对09年的考题展望:
要注意如何运用统计知识解释实际问题。立体几何题:
2006年(理):
19、(本大题满分12分)
如图,P是边长为1的正六边形ABCDEF所在平面外一点, ,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明 ⊥ ;
(Ⅱ)求面 与面 所成二面角的大小。 解:(Ⅰ)在正六边形ABCDEF中, 为等腰三角形,
∵P在平面ABC内的射影为O,∴PO⊥平面ABF,∴AO为PA在平面ABF内的射影;∵O为BF中点,∴AO⊥BF,∴PA⊥BF。
(Ⅱ)设M为PB的中点,连结AM,MD.∵在三角形ABP中PA=PB
∴
∵斜线PB在平面ABC内的射影为OB,BF垂直于AD,由三垂线定理得PB垂直于AD。
(Ⅱ)以O为坐标原点,建立空间直角坐标系,P(0,0,1),A(0, ,0),B( ,0,0),D(0,2,0),∴ , ,
设平面PAB的法向量为 ,则 ,
得
设平面PDB的法向量为 ,则, ,
得 , ;即可求出2007年(理):
17.(本小题满分14分)
如图,在六面体 中,四边形 是边长为2的正方形,四边形 是边长为1的正方形, 平面
平面 ,
(Ⅰ)求证: 与AC共面, 与 共面.
(Ⅱ)求证:平面 平面 ;
(Ⅲ)求二面角 的大小(用反三角函数值表示).解法1(向量法):
以为原点,以所在直线分别为
则有.
(Ⅰ)证明:
.
.平行,共面与X,Y,Z建立空间直角坐标系与与平行,与共面(Ⅱ)证明: ,
与 是平面内的两条相交直线.
平面 .
又平面 过 .
平面 平面 .(Ⅲ)解: .
设 为平面 的法向量,
, .
于是 ,取 ,则 , .
设 为平面 的法向量,
, .
于是 ,取 ,则 , .
二面角 的大小为 .2008年(理):
18.(本小题满分12分)
如图,在四棱锥O-ABCD中,底面ABCD是边长为l的菱形,,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
(I)证明:直线MN∥平面OCD.
(II)求异面直线AB与MD所成角的大小.
(III)求点B到平面OCD的距离.E 方法一(综合法):
(Ⅰ)取 中点 ,连接 .
,
.
又 ,平面 平面 .
平面 .
(Ⅱ) ,
为异面直线 与 所成的角(或其补角).
作 于点 ,连接 .
平面 .
.
所以,AB与MD所成角的大小为 .(Ⅲ) 平面 ,点B和点A到平面OCD的距离相等,
连接OP,过点A作 于点Q.
平面OAP, .
又 平面OCD,线段AQ的长就是点A到平面OCD的距离.所以,点B到平面OCD的距离为2/3.方法二(向量法):
作 于P点.如图,分别以 所在直线为 轴建立直角坐标系.
,
(Ⅰ) , , .
设平面OCD的法向量为 ,则
.即
取 ,解得 .
,
平面 .
(Ⅱ)设AB与MD所成的角为 ,
,
AB与MD所成角的大小为 .(Ⅲ)设点B到平面OCD的距离为 ,则 为在向量
上的投影的绝对值.
由 ,
得
所以,点B到平面OCD的距离为 2006年(文):
19、同2006年(理)一样
2007年(文):
17、同2007年(理)一样
2008年(文):
19、同2008年(理)基本一样,是2008年(理)的2、3两小题。
立体几何题的特点:
1、三年基本上处于稳定状态,都是先证后求。证明题是在线面关系、面面关系上出题;求值题则是在“三个角”、“三个距离”上出题。
2、三年的文理科均保持一致。
3、方法选择上基本上是等距离,即坐标法、传统几何法两种解法都能行得通,无论是对习惯用坐标法还是习惯用几何法的考生都很公平,但考生最好能习惯于坐标法。
4、难度适中,证明及运算要求合理。
对2009年的展望:
要注意转化到同一平面上解决问题的平面几何相关知识运用;同时要注意载体是旋转体的问题。函数题:
2006年(理):
20已知函数 在R上有定义,对任何实数 和任何实数 ,都有
(Ⅰ)证明 ;
(Ⅱ)证明 其中k和h均为常数;
(Ⅲ)当(Ⅱ)中的 时,设 ,讨论在内的单调性并求极值。
证明(Ⅰ)令 ,则 ,∵ ,∴ 。
(Ⅲ)当 时,
令 ,得 ;
当 时, ,∴ 是单调递减函数;
当 时, ,∴ 是单调递增函数;
所以当 时,函数 在 内取得极小值,极小值为2007年(理):
18、设 , .
(Ⅰ)令 ,讨论 在 内的单调性并求极值;
(Ⅱ)求证:当 时,恒有 .(Ⅰ)解:根据求导法则有 ,
故 ,
于是 ,
故知 在内是减函数,在 内是增函数,所以,在 处取得极小值 .(Ⅱ)证明:由 知, 的极小值 .
于是由上表知,对一切 ,恒有 .
从而当 时,恒有 ,故 在 内单调增加.
所以当 时, ,即 .
故当 时,恒有 .2008年(理):
20、设函数 .
(Ⅰ)求函数 的单调区间;
(Ⅱ)已知 对任意 成立,求实数a的取值范围.解:(Ⅰ) .若 ,则 .
列表如下:
所以 的单调增区间为 ,单调减区间为 和 (Ⅱ)在 两边取对数,得 .
由于 ,所以 . ①
由(Ⅰ)的结果知,
当 时, .
为使①式对所有 成立,当且仅当 ,
即 .2006年(文):
(20)设函数 ,已知 是奇函数。
(Ⅰ)求b、c的值。
(Ⅱ)求 的单调区间与极值。
证明(Ⅰ)∵ ,∴ 。从而
=
是一个奇函数,所以 得 ,由奇函数定义得 ;
(Ⅱ)由(Ⅰ)知 ,从而 ,由此可知,
和 是函数是单调递增区间;
是函数 是单调递减区间;
在 时,取得极大值,极大值为 , 在 时,取得极小值,极小值为 。2007年(文):
20、设函数 , ,
其中 ,将 的最小值记为 .
(I)求 的表达式;
(II)讨论 在区间 内的单调性并求极值.解:(I)我们有
由于 故当 时, 达到其最小值 ,即
(II)我们有列表如下:极小值由此可见, 在区间 和 单调增加,在区间 单调减小,极小值为 ,极大值为 .2008年(文):
20设函数 为实数。
(Ⅰ)已知函数 在 处取得极值,求 a的值;
(Ⅱ)已知不等式 对任意 都成立,求实数的取值范围。解: (1) ,由于函数 在 时取得极值,所以 即
(2)由题设知: 对任意 都成立
即 对任意 都成立
于是 对任意都成立,即
于是的取值范围是 函数题三年的特点:
1、三年均在导数的运用范围内出题,处于稳定状态。
2、三年的文理科出题都不一样,主要受降低文科难度指导思想所支配的。
3、考察方法基本上是通法通则,除2006年第2小题对能力要求很高之外,其它题都很平和。
对2009年的展望:
依然会保持近三年的命题风格;理科要密切注意将函数方程与导数联系在一起的题目以及将倒数与定积分联系在一起的题目;对抽象函数题要再次引起注意。数列题:
2006年(理):
21数列 的前项和为 ,已知
(Ⅰ)写出 与 的递推关系式 ,并求 关于的 表达式;
(Ⅱ)设 ,求数列 的前 项和 。
解:由 得 即 ,所以 ,对 成立。
所以
(Ⅱ)由 得
2007年(理):
21某国采用养老储备金制度.公民在就业的第一年就交纳养老储备金,数目为 ,以后每年交纳的数目均比上一年增加 ,因此,历年所交纳的储备金数目 是一个公差为 的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.这就是说,如果固定年利率为 ,那么,在第n年末,第一年所交纳的储备金就变为 ,第二年所交纳的储备金就变为 ,.以 表示到第 年末所累计的储备金总额.
(Ⅰ)写出 与 的递推关系式;
(Ⅱ)求证: 其中 是一个等比数列 是一个等差数列.
解:(Ⅰ)我们有
(Ⅱ) , 对反复使用上述关系式,得
①
在①式两端同乘 ,得
②
②-①得
即
如果记
则
其中 是以 为首项,以 为公比的等比数列;是以为 首项,为公差的等差数列.2008年(理):
21、设数列 满足 , , 其中 为实数.
(Ⅰ)证明: 对任意 成立的充分必要条件是 ,
(Ⅱ)设 ,证明: , ;
(Ⅲ)设 ,证明: , 解:(Ⅰ)必要性: ,
又 , ,
即
充分性:设 对 用数学归纳法证明
当 时, .假设 ( ),
则 且
由数学归纳法知, 对所有 成立.(Ⅱ)设 ,当 时, .结论成立.
当 时,
,
,由(Ⅰ)知 , 且
(Ⅲ)设 ,当 时, 结论成立.
当 时,由(Ⅱ)知,
2006年(文):
21、在等差数列 中, ,前 项和 满足条件
(Ⅰ)求数列 的通项公式;
(Ⅱ)记 ,求数列 的前n项和 。
解:(Ⅰ)设等差数列 的公差为 ,由 得 所以 ,即 ,
=
(Ⅱ)由 ,得 。
所以 ,
当 时, ;
当 时,
即2007年(文):
21、同07年(理)一样2008年(文):
21设数列 满足 其中为 实数,且
(Ⅰ)求数列 的通项公式
(Ⅱ)设 , ,求数列 的前 项和 ;
(Ⅲ)若对任意成立,证明 解 (1)
当 时, 是首项为 ,公比为c的等比数列。
,即
当 时, 仍满足上式。
数列 的通项公式为 (2)由(1)得(3)由(1)知
若 ,则
由 对任意 成立,知 。下面证 ,用反证法
假设 ,由函数 的函数图象知,当 趋于无穷大时, 趋于无穷大
不能对 恒成立,导致矛盾。数列题三年的特点:
1、理科三年相比风格各异,但都考了递推数列。06年主要考了错位相减法、数学归纳法,07年主要考了迭代法,错位相减法,08年则主要考了迭代法、数学归纳法。
2、三年题的位置均在最后两题,都是区分度很高的题。
3、综合性强,08年达到了最强状态,对考生综合能力的要求非常高。
4、06年文科题是理科题的姐妹题但要求低于理科很多,07年文理科一样,文科题明显上了难度,08年又回到了06年的做法。
对09年的展望:
理科可能还不会直接出等差、等比数列。文理科在对前三年所考过的基本方法熟知基础上,要密切注意累加法、倒序法的应用,以及利用函数做载体考法,以做到有备无患。
解析几何题:
2006年(理):
22、如图,F为双曲线C: 的右焦点。P为双曲线C右支上一点,且位于轴上方,M为左准线上一点,o为坐标原点。已知四边形 为平行四边形,
(Ⅰ)写出双曲线C的离心率 与 的关系式;
(Ⅱ)当 时,经过焦点F且品行于OP的直线交双曲线于A、B点,若 ,求此时的双曲线方程。解:∵四边形 是平行四边形 ,∴ 作双曲线的右准线交 PM于H,
则
(Ⅱ)当 时 双曲线 为四边形 是菱形,所以直线OP的斜率为 ,则直线AB的方程为 ,代入到双曲线方程得:
又 ,由 得:
解得 ,则
所以 为所求。2007年(理):
19.(本小题满分12分)
如图,曲线G的方程为 .以原点O为圆心.以 为半径的圆分别与曲线G和y轴的正半轴相交于点A与点B.直线AB与x轴相交于点C.
(Ⅰ)求点A的横坐标a与点C的横坐标c
的关系式
(Ⅱ)设曲线上点的横坐标为a+2 ,
求证:直线CD的斜率为定值.
解:(Ⅰ)由题意知, .
因为 ,所以 .
由于 ,故有 .(1)
由点 的坐标知,
直线BC的方程为
又因点A在直线BC上,故
将(1)代入上式,得
解得 (Ⅱ)因为 ,所以直线的斜率为
所以直线CD的斜率为定值.2008年(理):
22. (本小题满分13分)
设椭圆 过点 ,且左焦点为 .
(Ⅰ)求椭圆C的方程;
(Ⅱ)当过点 的动直线 与椭圆C相交于两不同点A,B时,在线段AB上取点Q,满足 证明:点Q总在某定直线上.解:(Ⅰ)由题意:
解得
所求椭圆方程为
(Ⅱ)设点 的坐标分别为 ,
由题设知 均不为零,记
则 且
又A、P、B、Q四点共线,从而
于是
从而, …① …②
又点A,B在椭圆C上,即
…③ …④
① ②并结合③,④得
即点 总在定直线 上.2006年(文):
22、同2006年(理)一样2007年(文):
18.设F是抛物线 的焦点.
(I)过点 作抛物线G的切线,求切线方程;
(II)设A,B为抛物线G上异于原点的两点,且满足 ,延长AF,BF分别交抛物线于G点,求四边形ABCD面积的最小值.
解:(I)设切点 由 知抛物线在点处的切线斜率为 ,故所求切线方程为
即
因为点 在切线上.
所以 , , .
所求切线方程为(II)设 ,
由题意知,直线AC的斜率k存在,由对称性,不妨设
因直线AC过焦点 ,所以直线的方程为
点A,C的坐标满足方程组
得
由根与系数的关系知
因为 ,所以BD的斜率为 ,从而的方程为
同理可求得
当k=1时,等号成立.所以,四边形 面积的最小值为32.2008年(文):
22设椭圆 其相应于焦点 的准线方程为
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知过点 倾斜角为 的直线交椭圆C于A,B两点,求证:
(Ⅲ)过点 作两条互相垂直的直线分别交椭圆C于A,B和D,求 的最小值 解 :(1)由题意得:
椭圆C的方程为
由(1)知 是椭圆C的左焦点,离心率
设 为椭圆的左准线。则
作 , 与 轴交于点H(如图)
点A在椭圆上
?同理 (3)设直线AB的倾斜角为 ,由于 由(2)可得
,
当 时, 取得最小值解析几何题三年的特点:
1、三年的文理科考题均在直线和二次曲线的关系上出题,06年考了双曲线、07年考了抛物线、08年考了椭圆,在大的范围内追求变化。
2、理科06年考题的辅助载体是平面几何中的平行四边形,07年是圆,08年则是向量。
3、理科07年考题的位置靠前(主要是考虑整个试卷的整体难度)06、08均在最后一题位置上。
4、文科06年考题和理科一样,07年虽和理科不一样,但还是姐妹题,运算量虽不比理科小,但方法通俗;08年文科辅助载体是三角函数,小题虽多一题,但运算难度明显低于理科。
对09年的展望:
依然会在直线和二次曲线上出题,但理科题可能用极坐标、参数方程解方法更简便,要注意以函数为辅助载体的问题以及注意求轨迹方程问题。
四、对新增内容的探究
1、安徽09年新增内容考哪些?
09年是安徽实行新课标高考的第一年,按照省厅领导的指示,依然要保持稳定。为维持稳定,09年高考数学考试说明,在制定的过程中对新增考点进行了最大限度的限制,具体体现如下:
a、理科数学新增内容只考如下内容,其中必修内容的有幂函数、算法与框图、定积分、常用逻辑、几何概型、茎叶图。
选修内容有坐标系与参数方程、不等式选讲(只考几种证明方法和绝对值不等式)
b、文科除了算法框图外,基本上和08年没有变化。值得一提的是文科对算法框图要求可能比理科要高,这主要体现在这一内容是文科的选修内容。
2、08年新课标省份对新增内容考题参考:
江苏卷:
在平面直角坐标系xOy中,若D表示横坐标与纵坐标的绝均不大于2的点构成的区域,E表示到原点的距离不大于1的点构成的区域,向D内随机地投一点,则落在E中的概率是 .(几何概型)
7.某地区为了解70~80岁老人的日睡眠时间(单位:t),现随机地选出50名做调查,下表是日睡眠时间频率分布表:在上述统计数据的分析中,一部分计算见算法流程图,则输出的S的值为 6.42 . 解:根据算法流程图中的S S+Gi·Fi可知21、A题为平面几何证明题,B题为矩阵(略)
C、.选修4—4 参数方程与极坐标
在平面直角坐标系xOy中,点P(x,y)是椭圆 上的一个动点,求S=x+y的最大值.21、D.选修4—5 不等式证明选讲
设a,b,c为正实数,求证:
证明:
当且仅当a=b=c,即a=b=c= 时,等号成立广东卷:
6.已知命题 所有有理数都是实数,命题 正数的对数都是负数,则下列命题中为真命题的是( D )
A B
C D
9.阅读图3的程序框图,若输入 ,
则输a= 12 ,i= 3 . 13(坐标系与参数方程选做题) 已知曲线C1,C2的极坐标方程分别 为 , , 则曲线与交点的极坐标为 .
14(不等式选讲选做题)已知 , 若关于x的方程 有实根,则a的取值范围是 . 宁夏海南卷:
5.右面的程序框图,如果输入三个实数a,b,c,要求输出这三
个数中最大的数,那么在空白的判断框中,应该填入下面四个选
项中的(A)
A.c>x B.x>c C.c>b D.b>c 10.由直线,x=2,曲线及x轴所围图形的面积为( D )
A. B. C. D.16.从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),结果如下:
甲品种:271 273 280 285 285 287 292 294 295 301 303 303 307
308 310 314 319 323 325 325 328 331 334 337 352
乙品种:284 292 295 304 306 307 312 313 315 315 316 318 318
320 322 322 324 327 329 331 333 336 337 343 356
由以上数据设计了如下茎叶图
根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论:1 2 (此题说法较多,抓住1、均值 2、方差即可)22、是平面几何证明题(略)
23、坐标系与参数方程
已知曲线C1: (为参数),曲线C2: (t为参数).
(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线 .写出 的参数方程. 公共点的个数和C1,C2公共点的个数是否相同?说明你的理由.山东卷:
6.右图是一个几何体的三视图,根据图中数据,
可得该几何体的表面积是(D )
A. B.
C. D.
8.右图是根据《山东统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为( B )
A.304.6 B.303.6
C.302.6 D.301.6
13.执行右边的程序框图,若 ,
则输出的 4 .
14.设函数 若 ,
则的 值为 . 3、 对以上试验区新内容考试特点分析:
a、所有省份都考了框图,且都出在客观题里,难度都不大。
b、对于极坐标参数方程,有客观题,有解答题。即便是解答题也均属基本题。
c、对积分的考法各省只限于客观题且很容易。
d、茎叶图的考法也只限于客观题且难度也不大。
e、不等式选讲单独出题只有江苏一省份,其证明很直观,比较容易。
f、几何概型也只有江苏一省份出了一道客观题,属于几何概型最基本的考法。
根据以上分析;估计我省09年高考对新增内容的考察从难度到题型都不会有多大的变化。复习与对策一、夯实基础有备无患
1、夯实基础不吃亏
2、如何做到夯实基础
二、在复习迎考中,真正做到有意识有目标的培养学生的能力
1、全面复习,突出重点,加强联系
2、指导学生改变接受式的听课方式
3、“活”做题,借题拔能
4、处理好形式和实质的关系
5、帮助学生勇敢、塌实地面对平时的考试
祝新春快乐!
一、教育部国家命题考试中心的命题规则
二、首次安徽省高考命题形成了什么样的安徽特色?
三、安徽三年高考命题的比较与探究
四、对新增内容的探究
复习与对策
一、夯实基础有备无患
二、在复习迎考中,真正做到有意识有目标的培养学生的能力
回顾与展望一、教育部国家命题考试中心的命题规则
?考试难度系数在0.5~0.6之间
?易、中、难题的比例为3:5:2(选择题中容易题4个左右,中等难度题6个左右,难题2个左右,而难题的难度系数也只是在0.3~0.45之间)
?知识覆盖面在70%~80%之间
?试题力求保证有信度、效度、区分度、梯度二、首次安徽省高考命题形成了什么样的安徽特色?
?依然保持着国家命题中心的试卷模式
?文理科数学区别拉大,特别改变了文科数学平均分低的现状
?考查相关知识点单纯明确,不作细节纠缠
?力求体现公平性
a 背景公平
b 考生在考试方法选择上公平(如立体几何、数列解答题)三、安徽三年高考命题的比较与探究
1、客观题比较
a 题量基本上保持不变(只有07年少考了一道选择题)
b 考试内容基本保持稳定,大致上在集合、不等式、二次曲线、直线和圆、逻辑命题、三角函数的图像及性质、多面体与球、线性规划、二项式定理、数列与极限、抽象函数及基本函数的性质、导数的应用、反函数、平面向量、理科还有复数、统计(07、08两年都出了正态分布题)。估计2009年要在新增内容上出题,如:立体几何中的 三视图、幂函数、积分、框图、算法、坐标系与参数方程等等我想不超过四题。c 试题难度大多较平和,无偏题、怪题。
d 解题方法以直接法为主,同时兼顾间接法;
直接法和间接法所用时间差异不明显,意在注重基础,增加考题效度。
间接法主要是特殊值法、淘汰法、数形结合法,代人验证法。并无只有间接法能解而直接法不能解的题,也没有用间接法解很简单而直接发很繁的题目。2、解答题比较
三角解答题:
2006年(理):
17、已知
(Ⅰ)求 的值;
(Ⅱ)求的值。解:(Ⅰ)由 得
即 又 所以为所求。(Ⅱ)====因为2007年(理):
16 已知 为 的最
小正周期, ,且
求 的值. 本题主要考查周期函数、平面向量数量积与三角函数基本关系式,考查运算能力和推理能力.
解:因为 为 的最小正周期,故 .
因 ,又 .
故 .
由于 ,所以
.2008年(理):
17已知函数 .
(I)求函数 的最小正周期和图象的对称轴方程.
(II)求函数 在区间上的 值域.解:(Ⅰ)
周期 .
由 ,得 ( )
函数图象的对称轴方程为 ( ).2006年(文):
17、已知
(Ⅰ)求 的值;
(Ⅱ)求 的值。 解:(Ⅰ)由 ,得 ,所以
=
(Ⅱ)∵ ,
∴2007年(文):
16、解不等式
解:因为对任意 ,所以原不等式等价于.
即故解为.
所以原不等式的解集为2008年(文):
同2008年(理)一样 三角题的特点:
1、依然是在求值和函数性质上出题,实质依然是化简。
2、三年题所考的方法都是通法通则。
3、难度都不大,无论是对理科考生还是文科考生都起到了定心丸的作用。
对09年的展望:
依然会维持稳定的现状。要注意平面几何三角形背景下的运算问题以及解三角形问题。统计与概率题:2006年(理)
18、在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。用 表示所选用的两种不同的添加剂的芳香度之和。(以列表的形式给出结论,不必写计算过程)
的数学期望(Ⅰ)写出的分布列;
(Ⅱ)求
(要求写出计算过程或说明道理) 解(Ⅰ)
(Ⅱ)2007年(理)
20.在医学生物学试验中,经常以果蝇作为试验对象.一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子,6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.以 表示笼内还剩下的果蝇的只数.
(Ⅰ)写出的分布列(不要求写出计算过程);
(Ⅱ)求数学期望 ;
(Ⅲ)求 概率.20.本小题主要考查等可能场合下的事件概率的计算、离散型随机变量的分布列、数学期望的概念及其计算,考查分析问题及解决实际问题的能力
解:(Ⅰ)的分布列为:
(Ⅱ)数学期望为
(Ⅲ)所求的概率为.2008年(理)
19(本小题满分12分)
为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物.某人一次种植了n株沙柳.各株沙柳的成活与否是相互独立的,成活率为p,设 为成活沙柳的株数,数学期望 为3,标准差 为 .
(Ⅰ)求 的值,并写出 的分布列;
(Ⅱ)若有3株或3株以上的沙柳未成活,则需要补种,求需要补种沙柳的概率.解:由题意知,服从二 项分布 ,
.
(Ⅰ)由 ,得 从而
的分布列为
(Ⅱ)记“需要补种沙柳”为事件A,则 ,
得 ,
或 .2006年(文)
18、在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验。
(Ⅰ)求所选用的两种不同的添加剂的芳香度之和等于4的概率;
(Ⅱ)求所选用的两种不同的添加剂的芳香度之和不小于3的概率;
解:设“所选用的两种不同的添加剂的芳香度之和等于4”的事件为A,“所选用的两种不同的添加剂的芳香度之和不小于3”的事件为B
(Ⅰ)芳香度之和等于4的取法有2
种: 、 ,
故
(Ⅱ)芳香度之和等于1的取法有1种: ;芳香度之和等于2的取法有1种: ,故
2007年(文)
19.(本小题满分13分)
在医学生物试验中,经常以果蝇作为试验对象.一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.
(I)求笼内恰好剩下1只果蝇的概率;
(II)求笼内至少剩下5只果蝇的概率.解:以 表示恰剩下 只果蝇的事件 .
以 表示至少剩下 只果蝇的事件 .
当事件 发生时,第 只飞出的蝇子是苍蝇,
且在前 只飞出的蝇子中有1只是苍蝇,所以2008年(文)
18、(本小题满分12分)
在某次普通话测试中,为测试汉字发音水平,设置了10张卡片,每张卡片印有一个汉字的拼音,其中恰有3张卡片上的拼音带有后鼻音“g”.
(Ⅰ)现对三位被测试者先后进行测试,第一位被测试者从这10张卡片总随机抽取1张,测试后放回,余下2位的测试,也按同样的方法进行。求这三位被测试者抽取的卡片上,拼音都带有后鼻音“g”的概率。
(Ⅱ)若某位被测试者从10张卡片中一次随机抽取3张,求这三张卡片上,拼音带有后鼻音“g”的卡片不少于2张的概率。 18解:
(1)每次测试中,被测试者从10张卡片中随机
抽取1张卡片上,拼音带有后鼻音“g”的概率为 ,
因为三位被测试者分别随机抽取一张卡片的事件是相互独
立的,因而所求的概率为
(2)设 表示所抽取的三张卡片中,恰有张卡片带有后鼻音“g”的事件,且其相应的概率为 则
因而所求概率为
概率统计题的特点:
1、理科三年均在等可能性场合下的概率计算、离散型随机变量分不列、期望上出题(2008年多考了一个标准差);文科则基本上在等可能事件、互斥事件上出题。
2、三年的运算量都不大,只涉及简单的排列组合运算,理科甚至可不用排列组合运算。
3、07年的题几乎延续了06年的出题风格,08年则改变了出题风格。三年是一个稳中渐变的过程。
4、难点依然放在如何面对实际问题,能准确识别数学模型上,突出了识别数学模式能里的考察。
对09年的考题展望:
要注意如何运用统计知识解释实际问题。立体几何题:
2006年(理):
19、(本大题满分12分)
如图,P是边长为1的正六边形ABCDEF所在平面外一点, ,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明 ⊥ ;
(Ⅱ)求面 与面 所成二面角的大小。 解:(Ⅰ)在正六边形ABCDEF中, 为等腰三角形,
∵P在平面ABC内的射影为O,∴PO⊥平面ABF,∴AO为PA在平面ABF内的射影;∵O为BF中点,∴AO⊥BF,∴PA⊥BF。
(Ⅱ)设M为PB的中点,连结AM,MD.∵在三角形ABP中PA=PB
∴
∵斜线PB在平面ABC内的射影为OB,BF垂直于AD,由三垂线定理得PB垂直于AD。
(Ⅱ)以O为坐标原点,建立空间直角坐标系,P(0,0,1),A(0, ,0),B( ,0,0),D(0,2,0),∴ , ,
设平面PAB的法向量为 ,则 ,
得
设平面PDB的法向量为 ,则, ,
得 , ;即可求出2007年(理):
17.(本小题满分14分)
如图,在六面体 中,四边形 是边长为2的正方形,四边形 是边长为1的正方形, 平面
平面 ,
(Ⅰ)求证: 与AC共面, 与 共面.
(Ⅱ)求证:平面 平面 ;
(Ⅲ)求二面角 的大小(用反三角函数值表示).解法1(向量法):
以为原点,以所在直线分别为
则有.
(Ⅰ)证明:
.
.平行,共面与X,Y,Z建立空间直角坐标系与与平行,与共面(Ⅱ)证明: ,
与 是平面内的两条相交直线.
平面 .
又平面 过 .
平面 平面 .(Ⅲ)解: .
设 为平面 的法向量,
, .
于是 ,取 ,则 , .
设 为平面 的法向量,
, .
于是 ,取 ,则 , .
二面角 的大小为 .2008年(理):
18.(本小题满分12分)
如图,在四棱锥O-ABCD中,底面ABCD是边长为l的菱形,,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
(I)证明:直线MN∥平面OCD.
(II)求异面直线AB与MD所成角的大小.
(III)求点B到平面OCD的距离.E 方法一(综合法):
(Ⅰ)取 中点 ,连接 .
,
.
又 ,平面 平面 .
平面 .
(Ⅱ) ,
为异面直线 与 所成的角(或其补角).
作 于点 ,连接 .
平面 .
.
所以,AB与MD所成角的大小为 .(Ⅲ) 平面 ,点B和点A到平面OCD的距离相等,
连接OP,过点A作 于点Q.
平面OAP, .
又 平面OCD,线段AQ的长就是点A到平面OCD的距离.所以,点B到平面OCD的距离为2/3.方法二(向量法):
作 于P点.如图,分别以 所在直线为 轴建立直角坐标系.
,
(Ⅰ) , , .
设平面OCD的法向量为 ,则
.即
取 ,解得 .
,
平面 .
(Ⅱ)设AB与MD所成的角为 ,
,
AB与MD所成角的大小为 .(Ⅲ)设点B到平面OCD的距离为 ,则 为在向量
上的投影的绝对值.
由 ,
得
所以,点B到平面OCD的距离为 2006年(文):
19、同2006年(理)一样
2007年(文):
17、同2007年(理)一样
2008年(文):
19、同2008年(理)基本一样,是2008年(理)的2、3两小题。
立体几何题的特点:
1、三年基本上处于稳定状态,都是先证后求。证明题是在线面关系、面面关系上出题;求值题则是在“三个角”、“三个距离”上出题。
2、三年的文理科均保持一致。
3、方法选择上基本上是等距离,即坐标法、传统几何法两种解法都能行得通,无论是对习惯用坐标法还是习惯用几何法的考生都很公平,但考生最好能习惯于坐标法。
4、难度适中,证明及运算要求合理。
对2009年的展望:
要注意转化到同一平面上解决问题的平面几何相关知识运用;同时要注意载体是旋转体的问题。函数题:
2006年(理):
20已知函数 在R上有定义,对任何实数 和任何实数 ,都有
(Ⅰ)证明 ;
(Ⅱ)证明 其中k和h均为常数;
(Ⅲ)当(Ⅱ)中的 时,设 ,讨论在内的单调性并求极值。
证明(Ⅰ)令 ,则 ,∵ ,∴ 。
(Ⅲ)当 时,
令 ,得 ;
当 时, ,∴ 是单调递减函数;
当 时, ,∴ 是单调递增函数;
所以当 时,函数 在 内取得极小值,极小值为2007年(理):
18、设 , .
(Ⅰ)令 ,讨论 在 内的单调性并求极值;
(Ⅱ)求证:当 时,恒有 .(Ⅰ)解:根据求导法则有 ,
故 ,
于是 ,
故知 在内是减函数,在 内是增函数,所以,在 处取得极小值 .(Ⅱ)证明:由 知, 的极小值 .
于是由上表知,对一切 ,恒有 .
从而当 时,恒有 ,故 在 内单调增加.
所以当 时, ,即 .
故当 时,恒有 .2008年(理):
20、设函数 .
(Ⅰ)求函数 的单调区间;
(Ⅱ)已知 对任意 成立,求实数a的取值范围.解:(Ⅰ) .若 ,则 .
列表如下:
所以 的单调增区间为 ,单调减区间为 和 (Ⅱ)在 两边取对数,得 .
由于 ,所以 . ①
由(Ⅰ)的结果知,
当 时, .
为使①式对所有 成立,当且仅当 ,
即 .2006年(文):
(20)设函数 ,已知 是奇函数。
(Ⅰ)求b、c的值。
(Ⅱ)求 的单调区间与极值。
证明(Ⅰ)∵ ,∴ 。从而
=
是一个奇函数,所以 得 ,由奇函数定义得 ;
(Ⅱ)由(Ⅰ)知 ,从而 ,由此可知,
和 是函数是单调递增区间;
是函数 是单调递减区间;
在 时,取得极大值,极大值为 , 在 时,取得极小值,极小值为 。2007年(文):
20、设函数 , ,
其中 ,将 的最小值记为 .
(I)求 的表达式;
(II)讨论 在区间 内的单调性并求极值.解:(I)我们有
由于 故当 时, 达到其最小值 ,即
(II)我们有列表如下:极小值由此可见, 在区间 和 单调增加,在区间 单调减小,极小值为 ,极大值为 .2008年(文):
20设函数 为实数。
(Ⅰ)已知函数 在 处取得极值,求 a的值;
(Ⅱ)已知不等式 对任意 都成立,求实数的取值范围。解: (1) ,由于函数 在 时取得极值,所以 即
(2)由题设知: 对任意 都成立
即 对任意 都成立
于是 对任意都成立,即
于是的取值范围是 函数题三年的特点:
1、三年均在导数的运用范围内出题,处于稳定状态。
2、三年的文理科出题都不一样,主要受降低文科难度指导思想所支配的。
3、考察方法基本上是通法通则,除2006年第2小题对能力要求很高之外,其它题都很平和。
对2009年的展望:
依然会保持近三年的命题风格;理科要密切注意将函数方程与导数联系在一起的题目以及将倒数与定积分联系在一起的题目;对抽象函数题要再次引起注意。数列题:
2006年(理):
21数列 的前项和为 ,已知
(Ⅰ)写出 与 的递推关系式 ,并求 关于的 表达式;
(Ⅱ)设 ,求数列 的前 项和 。
解:由 得 即 ,所以 ,对 成立。
所以
(Ⅱ)由 得
2007年(理):
21某国采用养老储备金制度.公民在就业的第一年就交纳养老储备金,数目为 ,以后每年交纳的数目均比上一年增加 ,因此,历年所交纳的储备金数目 是一个公差为 的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.这就是说,如果固定年利率为 ,那么,在第n年末,第一年所交纳的储备金就变为 ,第二年所交纳的储备金就变为 ,.以 表示到第 年末所累计的储备金总额.
(Ⅰ)写出 与 的递推关系式;
(Ⅱ)求证: 其中 是一个等比数列 是一个等差数列.
解:(Ⅰ)我们有
(Ⅱ) , 对反复使用上述关系式,得
①
在①式两端同乘 ,得
②
②-①得
即
如果记
则
其中 是以 为首项,以 为公比的等比数列;是以为 首项,为公差的等差数列.2008年(理):
21、设数列 满足 , , 其中 为实数.
(Ⅰ)证明: 对任意 成立的充分必要条件是 ,
(Ⅱ)设 ,证明: , ;
(Ⅲ)设 ,证明: , 解:(Ⅰ)必要性: ,
又 , ,
即
充分性:设 对 用数学归纳法证明
当 时, .假设 ( ),
则 且
由数学归纳法知, 对所有 成立.(Ⅱ)设 ,当 时, .结论成立.
当 时,
,
,由(Ⅰ)知 , 且
(Ⅲ)设 ,当 时, 结论成立.
当 时,由(Ⅱ)知,
2006年(文):
21、在等差数列 中, ,前 项和 满足条件
(Ⅰ)求数列 的通项公式;
(Ⅱ)记 ,求数列 的前n项和 。
解:(Ⅰ)设等差数列 的公差为 ,由 得 所以 ,即 ,
=
(Ⅱ)由 ,得 。
所以 ,
当 时, ;
当 时,
即2007年(文):
21、同07年(理)一样2008年(文):
21设数列 满足 其中为 实数,且
(Ⅰ)求数列 的通项公式
(Ⅱ)设 , ,求数列 的前 项和 ;
(Ⅲ)若对任意成立,证明 解 (1)
当 时, 是首项为 ,公比为c的等比数列。
,即
当 时, 仍满足上式。
数列 的通项公式为 (2)由(1)得(3)由(1)知
若 ,则
由 对任意 成立,知 。下面证 ,用反证法
假设 ,由函数 的函数图象知,当 趋于无穷大时, 趋于无穷大
不能对 恒成立,导致矛盾。数列题三年的特点:
1、理科三年相比风格各异,但都考了递推数列。06年主要考了错位相减法、数学归纳法,07年主要考了迭代法,错位相减法,08年则主要考了迭代法、数学归纳法。
2、三年题的位置均在最后两题,都是区分度很高的题。
3、综合性强,08年达到了最强状态,对考生综合能力的要求非常高。
4、06年文科题是理科题的姐妹题但要求低于理科很多,07年文理科一样,文科题明显上了难度,08年又回到了06年的做法。
对09年的展望:
理科可能还不会直接出等差、等比数列。文理科在对前三年所考过的基本方法熟知基础上,要密切注意累加法、倒序法的应用,以及利用函数做载体考法,以做到有备无患。
解析几何题:
2006年(理):
22、如图,F为双曲线C: 的右焦点。P为双曲线C右支上一点,且位于轴上方,M为左准线上一点,o为坐标原点。已知四边形 为平行四边形,
(Ⅰ)写出双曲线C的离心率 与 的关系式;
(Ⅱ)当 时,经过焦点F且品行于OP的直线交双曲线于A、B点,若 ,求此时的双曲线方程。解:∵四边形 是平行四边形 ,∴ 作双曲线的右准线交 PM于H,
则
(Ⅱ)当 时 双曲线 为四边形 是菱形,所以直线OP的斜率为 ,则直线AB的方程为 ,代入到双曲线方程得:
又 ,由 得:
解得 ,则
所以 为所求。2007年(理):
19.(本小题满分12分)
如图,曲线G的方程为 .以原点O为圆心.以 为半径的圆分别与曲线G和y轴的正半轴相交于点A与点B.直线AB与x轴相交于点C.
(Ⅰ)求点A的横坐标a与点C的横坐标c
的关系式
(Ⅱ)设曲线上点的横坐标为a+2 ,
求证:直线CD的斜率为定值.
解:(Ⅰ)由题意知, .
因为 ,所以 .
由于 ,故有 .(1)
由点 的坐标知,
直线BC的方程为
又因点A在直线BC上,故
将(1)代入上式,得
解得 (Ⅱ)因为 ,所以直线的斜率为
所以直线CD的斜率为定值.2008年(理):
22. (本小题满分13分)
设椭圆 过点 ,且左焦点为 .
(Ⅰ)求椭圆C的方程;
(Ⅱ)当过点 的动直线 与椭圆C相交于两不同点A,B时,在线段AB上取点Q,满足 证明:点Q总在某定直线上.解:(Ⅰ)由题意:
解得
所求椭圆方程为
(Ⅱ)设点 的坐标分别为 ,
由题设知 均不为零,记
则 且
又A、P、B、Q四点共线,从而
于是
从而, …① …②
又点A,B在椭圆C上,即
…③ …④
① ②并结合③,④得
即点 总在定直线 上.2006年(文):
22、同2006年(理)一样2007年(文):
18.设F是抛物线 的焦点.
(I)过点 作抛物线G的切线,求切线方程;
(II)设A,B为抛物线G上异于原点的两点,且满足 ,延长AF,BF分别交抛物线于G点,求四边形ABCD面积的最小值.
解:(I)设切点 由 知抛物线在点处的切线斜率为 ,故所求切线方程为
即
因为点 在切线上.
所以 , , .
所求切线方程为(II)设 ,
由题意知,直线AC的斜率k存在,由对称性,不妨设
因直线AC过焦点 ,所以直线的方程为
点A,C的坐标满足方程组
得
由根与系数的关系知
因为 ,所以BD的斜率为 ,从而的方程为
同理可求得
当k=1时,等号成立.所以,四边形 面积的最小值为32.2008年(文):
22设椭圆 其相应于焦点 的准线方程为
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知过点 倾斜角为 的直线交椭圆C于A,B两点,求证:
(Ⅲ)过点 作两条互相垂直的直线分别交椭圆C于A,B和D,求 的最小值 解 :(1)由题意得:
椭圆C的方程为
由(1)知 是椭圆C的左焦点,离心率
设 为椭圆的左准线。则
作 , 与 轴交于点H(如图)
点A在椭圆上
?同理 (3)设直线AB的倾斜角为 ,由于 由(2)可得
,
当 时, 取得最小值解析几何题三年的特点:
1、三年的文理科考题均在直线和二次曲线的关系上出题,06年考了双曲线、07年考了抛物线、08年考了椭圆,在大的范围内追求变化。
2、理科06年考题的辅助载体是平面几何中的平行四边形,07年是圆,08年则是向量。
3、理科07年考题的位置靠前(主要是考虑整个试卷的整体难度)06、08均在最后一题位置上。
4、文科06年考题和理科一样,07年虽和理科不一样,但还是姐妹题,运算量虽不比理科小,但方法通俗;08年文科辅助载体是三角函数,小题虽多一题,但运算难度明显低于理科。
对09年的展望:
依然会在直线和二次曲线上出题,但理科题可能用极坐标、参数方程解方法更简便,要注意以函数为辅助载体的问题以及注意求轨迹方程问题。
四、对新增内容的探究
1、安徽09年新增内容考哪些?
09年是安徽实行新课标高考的第一年,按照省厅领导的指示,依然要保持稳定。为维持稳定,09年高考数学考试说明,在制定的过程中对新增考点进行了最大限度的限制,具体体现如下:
a、理科数学新增内容只考如下内容,其中必修内容的有幂函数、算法与框图、定积分、常用逻辑、几何概型、茎叶图。
选修内容有坐标系与参数方程、不等式选讲(只考几种证明方法和绝对值不等式)
b、文科除了算法框图外,基本上和08年没有变化。值得一提的是文科对算法框图要求可能比理科要高,这主要体现在这一内容是文科的选修内容。
2、08年新课标省份对新增内容考题参考:
江苏卷:
在平面直角坐标系xOy中,若D表示横坐标与纵坐标的绝均不大于2的点构成的区域,E表示到原点的距离不大于1的点构成的区域,向D内随机地投一点,则落在E中的概率是 .(几何概型)
7.某地区为了解70~80岁老人的日睡眠时间(单位:t),现随机地选出50名做调查,下表是日睡眠时间频率分布表:在上述统计数据的分析中,一部分计算见算法流程图,则输出的S的值为 6.42 . 解:根据算法流程图中的S S+Gi·Fi可知21、A题为平面几何证明题,B题为矩阵(略)
C、.选修4—4 参数方程与极坐标
在平面直角坐标系xOy中,点P(x,y)是椭圆 上的一个动点,求S=x+y的最大值.21、D.选修4—5 不等式证明选讲
设a,b,c为正实数,求证:
证明:
当且仅当a=b=c,即a=b=c= 时,等号成立广东卷:
6.已知命题 所有有理数都是实数,命题 正数的对数都是负数,则下列命题中为真命题的是( D )
A B
C D
9.阅读图3的程序框图,若输入 ,
则输a= 12 ,i= 3 . 13(坐标系与参数方程选做题) 已知曲线C1,C2的极坐标方程分别 为 , , 则曲线与交点的极坐标为 .
14(不等式选讲选做题)已知 , 若关于x的方程 有实根,则a的取值范围是 . 宁夏海南卷:
5.右面的程序框图,如果输入三个实数a,b,c,要求输出这三
个数中最大的数,那么在空白的判断框中,应该填入下面四个选
项中的(A)
A.c>x B.x>c C.c>b D.b>c 10.由直线,x=2,曲线及x轴所围图形的面积为( D )
A. B. C. D.16.从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),结果如下:
甲品种:271 273 280 285 285 287 292 294 295 301 303 303 307
308 310 314 319 323 325 325 328 331 334 337 352
乙品种:284 292 295 304 306 307 312 313 315 315 316 318 318
320 322 322 324 327 329 331 333 336 337 343 356
由以上数据设计了如下茎叶图
根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论:1 2 (此题说法较多,抓住1、均值 2、方差即可)22、是平面几何证明题(略)
23、坐标系与参数方程
已知曲线C1: (为参数),曲线C2: (t为参数).
(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线 .写出 的参数方程. 公共点的个数和C1,C2公共点的个数是否相同?说明你的理由.山东卷:
6.右图是一个几何体的三视图,根据图中数据,
可得该几何体的表面积是(D )
A. B.
C. D.
8.右图是根据《山东统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为( B )
A.304.6 B.303.6
C.302.6 D.301.6
13.执行右边的程序框图,若 ,
则输出的 4 .
14.设函数 若 ,
则的 值为 . 3、 对以上试验区新内容考试特点分析:
a、所有省份都考了框图,且都出在客观题里,难度都不大。
b、对于极坐标参数方程,有客观题,有解答题。即便是解答题也均属基本题。
c、对积分的考法各省只限于客观题且很容易。
d、茎叶图的考法也只限于客观题且难度也不大。
e、不等式选讲单独出题只有江苏一省份,其证明很直观,比较容易。
f、几何概型也只有江苏一省份出了一道客观题,属于几何概型最基本的考法。
根据以上分析;估计我省09年高考对新增内容的考察从难度到题型都不会有多大的变化。复习与对策一、夯实基础有备无患
1、夯实基础不吃亏
2、如何做到夯实基础
二、在复习迎考中,真正做到有意识有目标的培养学生的能力
1、全面复习,突出重点,加强联系
2、指导学生改变接受式的听课方式
3、“活”做题,借题拔能
4、处理好形式和实质的关系
5、帮助学生勇敢、塌实地面对平时的考试
祝新春快乐!
同课章节目录
